






数学八年级上册第十四章 实数14.3 实数课文配套ppt课件
展开(1)正数的平方根怎样表示?平方根的性质是什么?
(2)什么叫做算术平方根?什么样的数有算术平方根?
(3)立方根的概念是什么?它有怎样的性质?
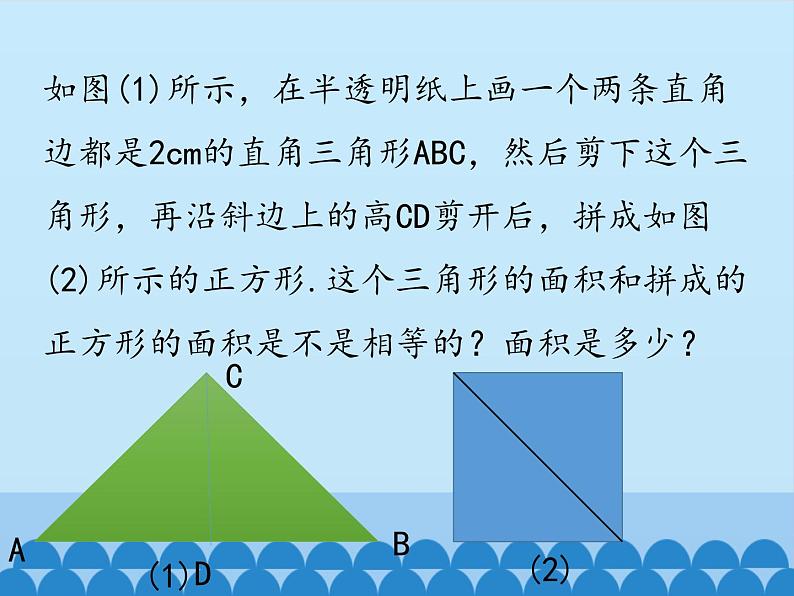
如图(1)所示,在半透明纸上画一个两条直角边都是2cm的直角三角形ABC,然后剪下这个三角形,再沿斜边上的高CD剪开后,拼成如图(2)所示的正方形.这个三角形的面积和拼成的正方形的面积是不是相等的?面积是多少?
是整数吗? 的平方等于2吗?你认为有平方后等于2的整数吗?2. 是分数吗? 的平方等于2吗?你认为有平方后等于2的分数吗?3. 会是有理数吗?
(1)什么叫做有理数?(2)整数和分数都可以化成怎样的小数?
分数可以写成有限小数或无限循环小数.
有理数总可以写成有限小数或无限循环小数.
我们把无限不循环小数叫做无理数.
(1)判断一个数是不是无理数,一是看它是不是无限小数;二是看它是不是不循环小数,满足“无限”和“不循环”这两个条件,才是无理数.
(2)初中阶段所学的无理数主要包含以下几种:①特殊意义的数:如圆周率π及含π的一些数,如2-π等;②开方开不尽的数,如 , , 等;③特殊结构的数,如2.01001000100001……(每两个1之间依次多一个0)等.
(3)带根号的数不一定是无理数,如:它们不是无理数,而是有理数,无理数也不一定带根号,如 .
一般a是一个正无理数,那么-a是一个负无理数.我们把有理数和无理数统称实数.
想一想:有理数与无理数有什么区别?(1)有理数是有限小数或无限循环小数,而无理数是无限不循环小数.(2)所有的有理数都能写成分数的形式(整数可以看成分母是1的分数),而无理数不能化成分数的形式.
小故事:2500年前,当时的数学家毕达哥拉斯认为“宇宙中存在的数都是有理数”,拥护他的人认为毕达哥拉斯是至高无上的,他所说的一切都是真理.但后来有一位年轻学者希伯索斯发现边长为1的正方形的对角线的长不能用有理数来表示,这个发现动摇了毕达哥拉斯学派的信条,为此希伯索斯被投入大海.他为真理献出了宝贵的生命,但真理是不可战胜的.后来人们正视了希伯索斯的发现,也就是我们前面谈到的x2=2中的x不是有理数.
我们现在所学的知识都是前人给我们总结出来的,我们一方面应积极地学习这些经验,另一方面我们也不能死搬教条,要大胆质疑,如不这样科学就会停滞不前,要向希伯索斯学习,学习他为追求真理而大无畏的精神.
1.实数
有理数:总可以化成有限小数或无限循环小数 无理数:无限不循环小数
2.无理数满足的三个条件:(1)首先是小数;(2)其次是小数中的无限小数;(3)并且是无限小数中的不循环小数.
1.(2015·绥化中考)在实数0,π, , , 中,无理数的个数有 ( )
A. 1个B. 2个C. 3个D. 4个
解析:π, 是无理数.故选B.
2. 下列说法:①带根号的数是无理数;②不含根号的数一定是有理数;③无理数是开方开不尽的数;④无限小数是无理数;⑤π是无理数.其中正确的有( )A.4个B.3个C.2个D.1个
解析:①带根号的数不一定是无理数,如 ;②不含根号的数不一定是有理数,如无限不循环小数;③开方开不尽的数是无理数;④无限不循环小数是无理数;⑤π是无理数,该说法正确.故选D.
3 .(2015·扬州中考)实数0是 ( )A.有理数B.无理数C.正数D.负数
4.下列分数中,能化为有限小数的是( )A. B.C. D.
解析:选项A,B,D是无限循环小数,C中的结果是0.2.故选C.
解析:0是有理数.故选A.
5.下列关于数的说法正确的是( )A.有理数都是有限小数B.无限小数都是无理数C.无理数都是无限小数D.有限小数是无理数
解析:A.无限循环小数是有理数,故A错误;B.无限循环小数是有理数,故B错误;C.无理数是无限不循环小数,故C正确;D.无理数是无限不循环小数,故D错误.故选C.
解析:2的平方根及立方根均为无理数,共3个;3的平方根及立方根均为无理数,共3个;4的立方根是无理数,共1个;5的平方根及立方根均为无理数,共3个;6的平方根及立方根均为无理数,共3个;7的平方根及立方根均为无理数,共3个;8的平方根是无理数,共2个;9的立方根是无理数,共1个;10的平方根及立方根均为无理数,共3个.综上,可得无理数共22个.故填22.
6.在0,1,2,3,4,5,6,7,8,9,10的平方根及立方根中,无理数有 个.
7.面积为3的正方形的边长 有理数;面积为4的正方形的边长 有理数.(填“是”或“不是”)
解析:∵正方形的面积为3,∴正方形的边长为 故面积为3的正方形的边长不是有理数,∵正方形的面积为4,∴正方形的边长为2,故面积为4的正方形的边长是有理数.
初中数学冀教版八年级上册14.3 实数教案配套课件ppt: 这是一份初中数学冀教版八年级上册14.3 实数教案配套课件ppt,共19页。PPT课件主要包含了想一想,观察与思考,解从小到大排列为,做一做,知识拓展,例题讲解,课堂小结等内容,欢迎下载使用。
2021学年14.3 实数教学演示课件ppt: 这是一份2021学年14.3 实数教学演示课件ppt,共19页。PPT课件主要包含了按定义分类等内容,欢迎下载使用。
初中数学冀教版八年级上册14.3 实数教学演示课件ppt: 这是一份初中数学冀教版八年级上册14.3 实数教学演示课件ppt,共19页。PPT课件主要包含了与互为倒数,实数的性质,练一练,b+a,a+b+c,abc,实数的运算,ab+ac,ba+ca,14-π等内容,欢迎下载使用。













