初中数学人教版九年级上册24.1.2 垂直于弦的直径教学设计

这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径教学设计，共7页。教案主要包含了证明定理，归纳定理，巩固定理，解决问题等内容，欢迎下载使用。
教学目标：
1.知识与技能：
（1）通过观察以及动手操作,理解圆的轴对称性。
（2）掌握垂径定理的内容及几何语言。
（3）会用垂径定理解决有关的证明与计算问题。
2.过程与方法：
（1）通过探索圆的对称性及相关性质,培养学生动手操作能力及观察、分析、逻辑推理和归纳概括能力。
（2）经历探究垂径定理的过程,体会和理解研究几何图形的多种方法。
3.情感态度与价值观：
（1）通过探究垂径定理的活动, 并引入实际问题，使学生知道数学在实际生活中的用处，激发学生探究、发现数学问题的兴趣。
（2）培养学生观察能力,激发学生的好奇心和求知欲,并从数学学习活动中获得成功的体验。
教学重难点：
【重点】垂径定理及其应用
【难点】探索并证明垂径定理,利用垂径定理解决一些实际问题。
教学准备：
多媒体课件、自制圆形纸片、导学案、作图工具
一、情境引入
我校总务处的李师傅遇到一件麻烦事，因我校一处圆形下水道破裂，他准备更换新管道，但只知道污水面宽60cm，水面至管道顶部10cm ，你能帮李师傅计算一下他应准备内径多大的管道吗？
二、实践探究
1.活动1: 我们在学轴对称的时候已经学过
圆是 轴对称 图形， 任何一条直径所在的直线 都是圆的对称轴。
将你手中的圆形纸片沿着它的任意一条直径对折，重复做几次，验证圆的这一特性。课本中有证明圆是轴对称图形的方法，课前已经让大家预习过了，现在大家再来看一下，进行巩固。
2.活动2: 在圆形纸片上操作：
①找出圆心，记作O
②作出一条直径，与⊙O交于C、D
③在⊙O上的任意找一点A，过点A作一条弦AB使AB⊥CD, 交⊙O于点B，垂足为E。沿着直径CD对折，你发现了什么？有哪些相等的线段和弧？
观察发现：
点A与 重合，AE与 重合,
弧AC与 重合，弧AD与 重合。
相等的线段: ，
相等的弧: .
思考：
如果AB是⊙O的一条直径呢？以上结论还会成立吗？
【证明定理】
动手操作之后，我们现在来进行理论证明。
学生用自己的方法证明，之后同学之间分享方法。
①证明“AE=BE”
②证明“弧相等”
【归纳定理】
根据上面的证明，提炼出“两个条件”“三个结论”并得出 “垂径定理”。
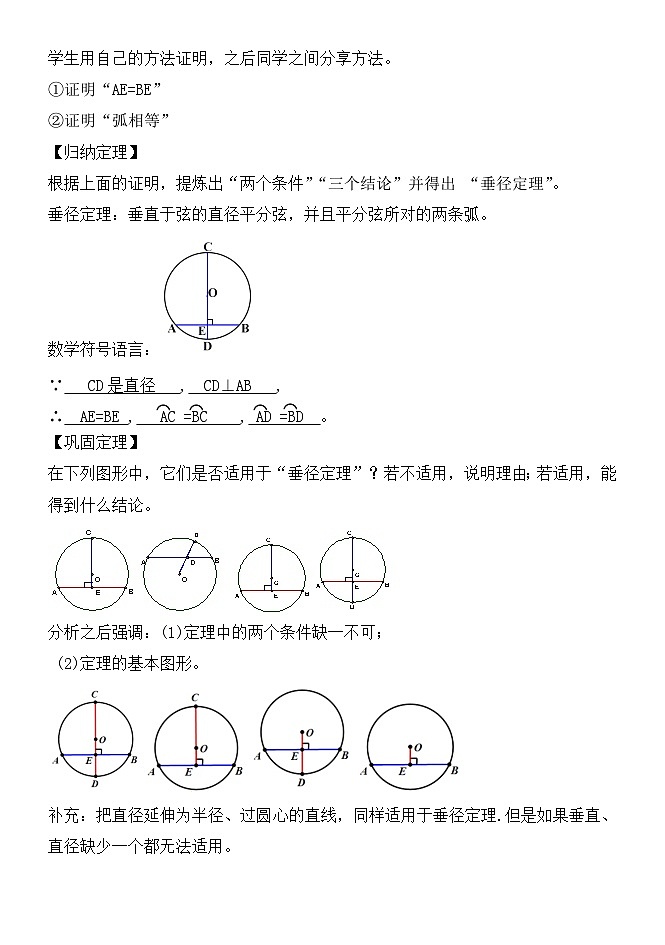
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。
数学符号语言：
⌒
⌒
⌒
⌒
∵ CD是直径 , CD⊥AB ,
∴ AE=BE , AC =BC , AD =BD 。
【巩固定理】
在下列图形中，它们是否适用于“垂径定理”？若不适用，说明理由；若适用，能得到什么结论。
O
E
D
C
A
B
分析之后强调：(1)定理中的两个条件缺一不可；
(2)定理的基本图形。
补充：把直径延伸为半径、过圆心的直线，同样适用于垂径定理.但是如果垂直、直径缺少一个都无法适用。
三、典例精析
例1 (2023河北省中考题)装有水的水槽放置在水平台面上，其横截面是以AB为直径的半圆O，AB=50cm，如图所示MN为水面截线，GH为台面截线，MN∥GH。
计算：图中，已知MN=48cm，作OC⊥MN于点C。求OC的长。
解：连接OM
∵O为圆心，OC⊥MN于点C,MN=48cm
∴MC=12MN=24cm
∵AB=50cm
∴OM=12AB=25cm
∴在RT△OMC中
例2 思考
若圆的半径为R，一条弦长为a，圆心到弦的距离为d（弦心距），则R、a、d三者之间的关系式是 。
四、当堂评测
1.如图1，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是（ ）。
A．4 B．6 C．7 D．8
2.如图2，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM的长的最小值为 ，最大值为______。
3.如图3，已知⊙O的半径为13mm，弦AB=10mm，则圆心O到AB的距离是（ ）。
A．3 mm B．4 mm C．12 mm D．5 mm
4.如图4，AB为圆O的弦，圆O的半径为5，OC⊥AB于点D，交圆O于点C，且CD=2，则AB的长是____。
图2
图1
图4
图3
5.已知：⊙O中弦AB∥CD。
求证：弧AC＝弧BD
6.如图，⊙O中弦CD交半径OE于点A，交半径OF于点B，若OA＝OB。
求证：AC＝BD。
证明：过点O作OG⊥CD于点G
∵OG过圆心
∴CG＝DG
∵OA＝OB
∴AG＝BG
∴CG－AG＝DG－BG
∴AC＝BD
方法总结：解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，构造由半径、半弦、弦心距组成的直角三角形利用勾股定理计算或建立方程。
【解决问题】
我校总务处的李师傅遇到一件麻烦事，因我校一处圆形下水道破裂，他准备更换新管道，但只知道污水面宽60cm，水面至管道顶部10cm，你能帮李师傅计算一下他应准备内径多大的管道吗？
五、课堂总结
本节课结束，你学到了什么？
1.垂径定理的内容及基本图形——如下
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。
2.计算中三个量的关系——如图，
3.证明中常用的辅助线——连半径，作弦心距，作垂直于弦的直径。
解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，构造由半径、半弦、弦心距组成的直角三角形利用勾股定理计算或建立方程。
六、巩固作业
必做题：
1.如图，CD是⊙O的直径，弦AB⊥CD于E，CE=1，AB=10，求直径CD的长。
2.已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。求证：AC＝BD。
选做题：
1.已知⊙O的半径为5cm，弦AB=8cm,CD=6cm，且AB∥CD，求两弦之间的距离。
2.如图，在平面直角坐标系x0y中，直径为10的OE交x轴于点A，B,交y轴于点C、D，且点A、B的坐标分別为（-2,0）,（4,0）。试求圆心E和点C、D的坐标。