专题04 相似三角形的四种基本模型-2023年初中数学9年级下册同步压轴题（学生版）

这是一份专题04 相似三角形的四种基本模型-2023年初中数学9年级下册同步压轴题（学生版），文件包含专题04相似三角形的四种基本模型-2023年初中数学9年级下册同步压轴题教师版含解析docx、专题04相似三角形的四种基本模型-2023年初中数学9年级下册同步压轴题学生版docx等2份试卷配套教学资源，其中试卷共65页， 欢迎下载使用。


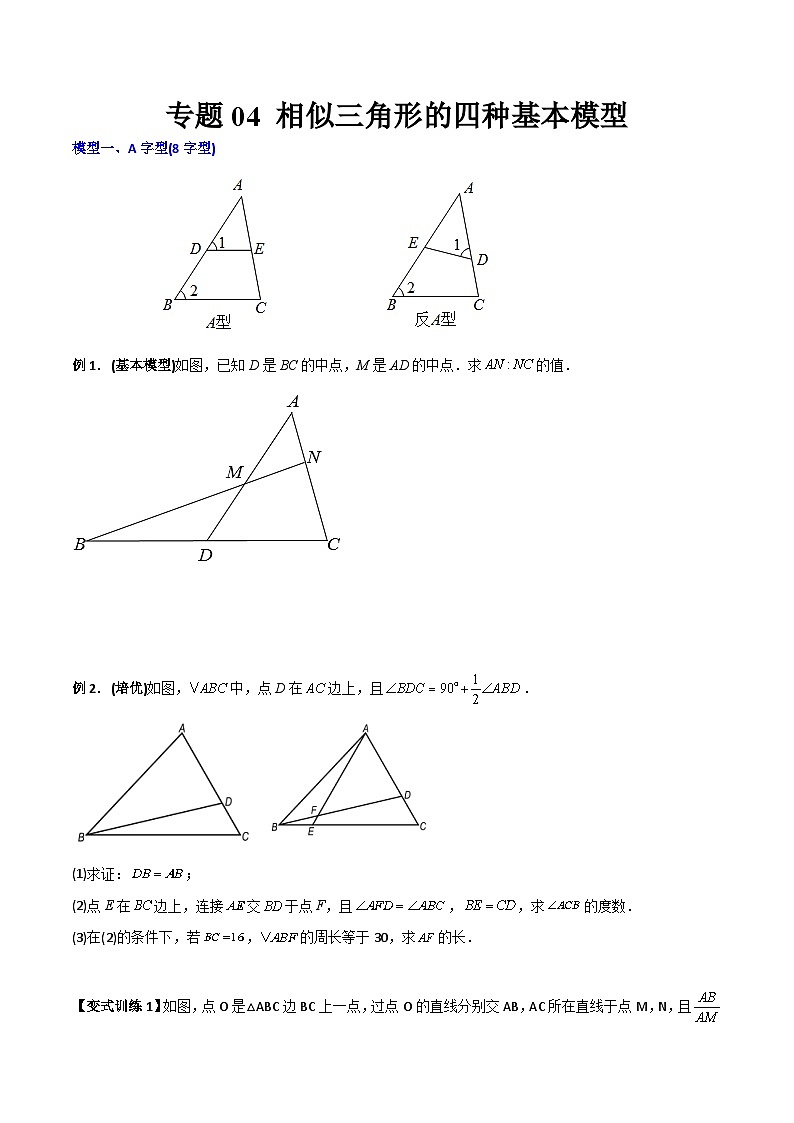
例1．(基本模型)如图，已知D是BC的中点，M是AD的中点．求的值．
例2．(培优)如图，中，点D在边上，且．

(1)求证：；
(2)点E在边上，连接交于点F，且，，求的度数．
(3)在(2)的条件下，若，的周长等于30，求的长．
【变式训练1】如图，点O是△ABC边BC上一点，过点O的直线分别交AB，AC所在直线于点M，N，且＝m，＝n．
(1)若点O是线段BC中点．
①求证：m+n＝2；
②求mn的最大值；
(2)若＝k(k≠0)求m，n之间的关系(用含k的代数式表示)．
【变式训练2】矩形ABCD中，AB＝8，AD＝12．将矩形折叠，使点A落在点P处，折痕为DE．
(1)如图①，若点P恰好在边BC上，连接AP，求的值；
(2)如图②，若E是AB的中点，EP的延长线交BC于点F，求BF的长．
模型二、X(8)字型

X字型(平行) 反X字型(不平行)
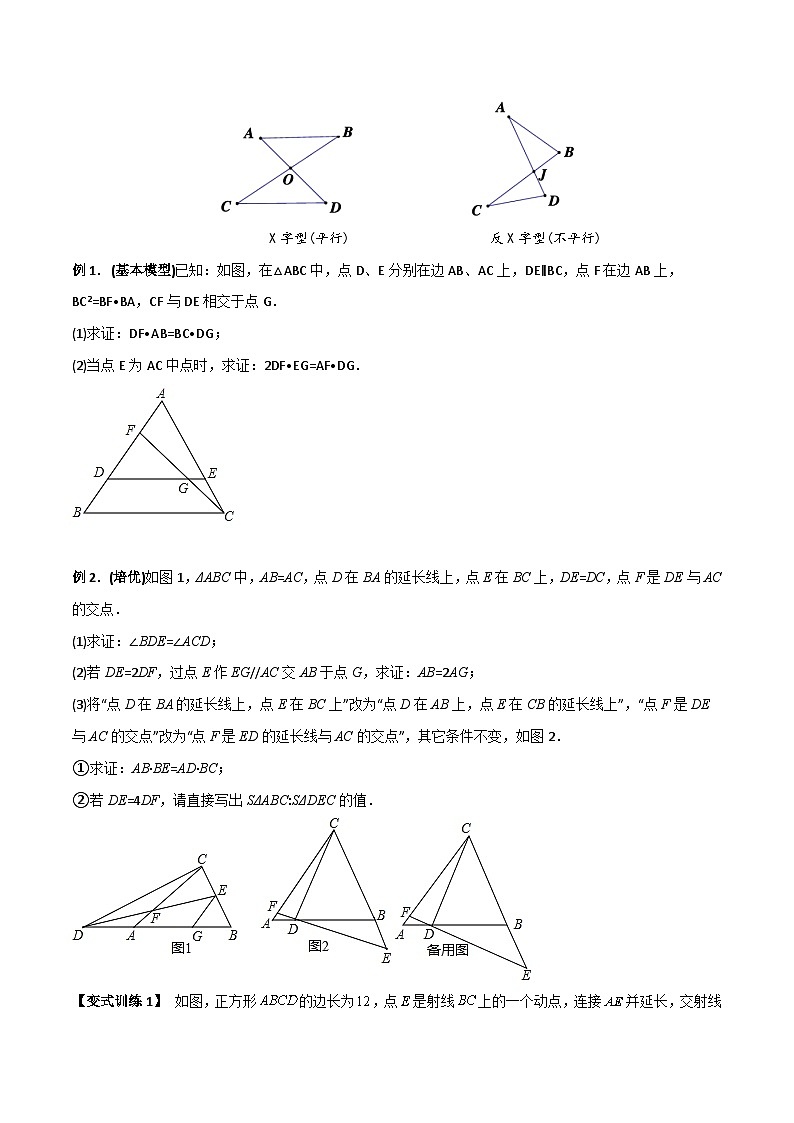
例1．(基本模型)已知：如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，点F在边AB上，BC2=BF•BA，CF与DE相交于点G．
(1)求证：DF•AB=BC•DG；
(2)当点E为AC中点时，求证：2DF•EG=AF•DG．
例2．(培优)如图1，ΔABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=DC，点F是DE与AC的交点．
(1)求证：∠BDE=∠ACD；
(2)若DE=2DF，过点E作EG//AC交AB于点G，求证：AB=2AG；
(3)将“点D在BA的延长线上，点E在BC上”改为“点D在AB上，点E在CB的延长线上”，“点F是DE与AC的交点”改为“点F是ED的延长线与AC的交点”，其它条件不变，如图2．
①求证：AB·BE=AD·BC；
②若DE=4DF，请直接写出SΔABC:SΔDEC的值．
【变式训练1】 如图，正方形的边长为，点是射线上的一个动点，连接并延长，交射线于点，将沿直线翻折，点落在点处．

(1)当时，如图，延长，交于点，
①的长为________；
②求证：．
(2)当点恰好落在对角线上时，如图，此时的长为________；________；
(3)当时，求的正弦值．
【变式训练2】如图1，在矩形ABCO中，OA＝8，OC＝6，D，E分别是AB，BC上一点，AD＝2，CE＝3，OE与CD相交于点F．
(1)求证：OE⊥CD；
(2)如图2，点G是CD的中点，延长OG交BC于H，求CH的长．
【变式训练3】已知：矩形ABCD中，AB＝6，BC＝8，点P是线段AD上一点，连接CP，点E在对角线AC上(不与点A，C重合)，∠CPE＝∠ACB，PE的延长线与BC交于点F．
(1)如图1，当AP＝2时，求CF的长；
(2)如图2，当PF⊥BC时，求AP的长；
(3)当△PFC是等腰三角形时，求AP的长．
模型三、子母型
已知：∠ 1=∠2；结论：△ACD ∽△ABC
例1．(基本模型)如图，在△ABC中，点D在BC边上，点E在AC边上，且AD＝AB，∠DEC＝∠B．
(1)求证：△AED∽△ADC；
(2)若AE＝1，EC＝3，求AB的长．
例2.(培优)在Rt△ABC中，∠ACB=90°，点D为AB上一点．
(1)如图1，若CD⊥AB，求证：AC2=AD·AB；
(2)如图2，若AC=BC，EF⊥CD交CD于H，交AC于F，且，求的值；
(3)如图3，若AC=BC，点H在CD上，∠AHD=45°，CH=3DH，则tan∠ACH的值为________．
【变式训练1】在矩形中，，，是边上一点，交于点，过点作，交射线于点，交射线于点．
(1)如图，当点与点重合时，求的长．
(2)如图，当点在线段上时，设，，求与之间的函数关系式，并写出它的定义域．
(3)连接，当与相似时，求线段的长．
【变式训练2】如图，锐角△ABC中，CD，BE分别是AB，AC边上的高，垂足为D，E．
(1)求证：△ACD∽△ABE；
(2)若将点D，E连接起来，则△AED和△ABC能相似吗？说说你的理由．
【变式训练3】已知正方形的边长为4，点在边上，点在边上，且，和交于点．
(1)如图，求证：
①
②
(2)连接并延长交于点，
①若点为的中点(如图)，求的长．
②若点在边上滑动(不与点重合)，当取得最小值时，求的长．
模型四、旋转型
例1．(基本模型)在同一平面内，如图①，将两个全等的等腰直角三角形摆放在一起，点A为公共顶点，．如图②，若△ABC固定不动，把△ADE绕点A逆时针旋转，使AD、AE与边BC的交点分别为M、N点M不与点B重合，点N不与点C重合．
【探究】求证：．
【应用】已知等腰直角三角形的斜边长为4．
(1)的值为______．
(2)若，则MN的长为______．
例2．(培优)【问题发现】如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为斜边BC上一点(不与点B，C重合)，将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是______，位置关系是______；
【探究证明】如图2，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；
【拓展延伸】如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，过点C作CA⊥BD于A．将△ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角∠CAE为(0°＜＜360°)，当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．
【变式训练1】如图，等腰三角形ABC和等腰三角形ADE，其中AB＝AC，AD＝AE．
(1)如图1，若∠BAC＝90°，当C、D、E共线时，AD的延长线AF⊥BC交BC于点F，则∠ACE＝______；
(2)如图2，连接CD、BE，延长ED交BC于点F，若点F是BC的中点，∠BAC＝∠DAE，证明：AD⊥CD；
(3)如图3，延长DC到点M，连接BM，使得∠ABM＋∠ACM＝180°，延长ED、BM交于点N，连接AN，若∠BAC＝2∠NAD，请写出∠ADM、∠DAE它们之间的数量关系，并写出证明过程．
【变式训练2】［问题发现］
(1)如图1，在Rt△ABC中，，，点为的中点，以为一边作正方形，点与点重合，已知．请直接写出线段与的数量关系；
［实验研究］
(2)在(1)的条件下，将正方形绕点旋转至如图2所示的位置，连接，，．请猜想线段和的数量关系，并证明你的结论；
［结论运用］
(3)在(1)(2)的条件下，若的面积为8，当正方形旋转到，，三点共线时，请求出线段的长．
模型五、一线三垂直型
例1．(模型探究)【感知】如图①，在四边形ABCD中，点P在边AB上(点P不与点A、B重合)，．易证．(不需要证明)
【探究】如图②，在四边形ABCD中，点P在边AB上(点P不与点A、B重合)，．若，，，求AP的长．
【拓展】如图③，在中，，，点P在边AB上(点P不与点A、B重合)，连结CP，作，PE与边BC交于点E，当是等腰三角形时，直接写出AP的长．
例2．(培优)问题提出
(1)如图1，在矩形中，，点E为的中点，点F在上，过点E作交于点G．若，则的面积为_________．
问题探究
(2)如图2，在矩形中，，点P是边上一动点，点Q是的中点将．沿着折叠，点A的对应点是，将沿着折叠，点D的对应点是．请问是否存在这样的点P，使得点P、、在同一条直线上？若存在，求出此时的长度；若不存在，请说明理由．
问题解决
(3)某精密仪器厂接到生产一种特殊四边形金属部件的任务，部件要求：如图3，在四边形中，，点D到的距离为，且．若过点D作，过点A作的垂线，交于点E，交的延长线于点H，过点C作于点F，连接．设的长为，四边形的面积为．
①根据题意求出y与x之间的函数关系式；
②在满足要求和保证质量的前提下，仪器厂希望造价最低．已知这种金属材料每平方厘米造价60元，请你帮忙求出这种四边形金属部件每个的造价最低费用．
【变式训练1】问题提出：
(1)如图①，矩形ABCD中，AD＝6．点E为AD的中点．点F在AB上，过点E作EGAB交FC于点G．若EG＝7．则S△EFC＝ ．
问题探究：
(2)如图②．已知矩形ABCD纸片中．AB＝9，AD＝6，点P是CD边上一动点．点Q是BC的中点．将△ADP沿着AP折叠，在纸片上点D的对应点是，将△QCP沿着PQ折叠．在纸片上点C的对应点是．请问是否存在这样的点P．使得点P、、在同一条直线上？若存在，求出此时DP的长度．若不存在，请说明理由．
问题解决：
(3)某精密仪器厂接到生产一种特殊四边形金属部件的任务．部件要求：如图③，四边形ABCD中，AB＝4厘米，点C到AB的距离为5厘米，BC⊥CD．且BC＝CD．在满足要求和保证质量的前提下，仪器厂希望造价最低，已知这种金属材料每平方厘米造价50元．请问这种四边形金属部件每个的造价最低是多少元？(≈1.73)
【变式训练2】如图，矩形ABCD中，AB＝1，BC＝3，点E是边BC上一个动点(不与点B、C重合)，AE的垂线AF交CD的延长线于点F，点G在线段EF上，满足FG∶GE＝1∶2，设BE＝x．
(1)求证：；
(2)当点G在△ADF的内部时，用x的代数式表示∠ADG的余切；
(3)当∠FGD＝∠AFE时，求线段BE的长．
【变式训练3】如图1和图2，在平面直角坐标系中，点C的坐标为(0，4)，A是x轴上的一个动点，M是线段AC的中点．把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB．过B作x轴的垂线、过点C作y轴的垂线，两直线交于点D，直线DB交x轴于点E．设A点的横坐标为m．
(1)求证：△AOC∽△BEA；
(2)若m=3，则点B的坐标为 ；若m=﹣3，则点B的坐标为 ；
(3)若m＞0，△BCD的面积为S，则m为何值时，S=6？
(4)是否存在m，使得以B、C、D为顶点的三角形与△AOC相似？若存在，求此时m的值；若不存在，请说明理由．