山东省滨州市邹平市第一中学2022-2023学年高三上学期期中考试数学试题(含答案)

这是一份山东省滨州市邹平市第一中学2022-2023学年高三上学期期中考试数学试题(含答案)，共21页。试卷主要包含了选择题，多项选择题，填空题，双空题，解答题等内容，欢迎下载使用。


一、选择题
1、已知集合，，则( )
A.B.C.D.
2、已知点O是平面内任意一点，则“存在，使得”是“A，B，C三点共线”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
3、已知等比数列，，则( )
A.1B.2C.4D.8
4、三角形的三边分别为a，b，c，秦九韶公式和海伦公式是等价的，都是用来求三角形的面积.印度数学家婆罗摩笈多在公元7世纪的一部论及天文的著作中，给出若四边形的四边分别为a，b，c，d，则（为一组对角和的一半）.已知四边形四条边长分别为3，4，5，6，则四边形最大面积为( )
A.21B.C.D.
5、已知为第三象限角，，则( )
A.B.C.D.
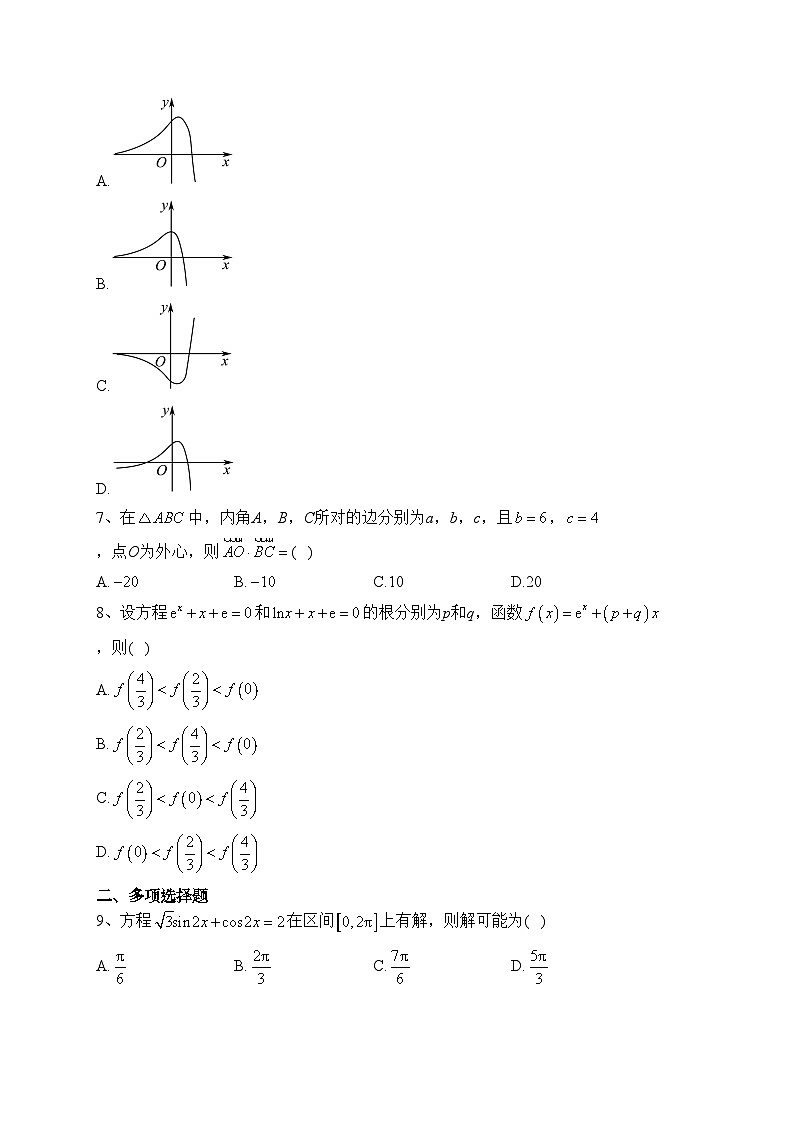
6、函数的图象大致为( )
A.
B.
C.
D.
7、在中，内角A，B，C所对的边分别为a，b，c，且，，点O为外心，则( )
A.B.C.10D.20
8、设方程和的根分别为p和q，函数，则( )
A.
B.
C.
D.
二、多项选择题
9、方程在区间上有解，则解可能为( )
A.B.C.D.
10、已知等差数列，前n项和为，，则下列结论正确的是( )
A.
B.的最大值为
C.的最小值为
D.
11、已知，，则下列不等式一定成立的是( )
A.
B.
C.
D.
12、在中，内角A，B，C所对的边分别为a，b，c，且，则下列结论正确的是( )
A.
B.若，则为直角三角形
C.若面积为1，则三条高乘积平方的最大值为
D.若D为边上一点，且，，则的最小值为
三、填空题
13、已知，，则与夹角的余弦值为_________.
14、已知函数在R上单调递增，则a的取值范围为_________.
15、已知是定义域为R的奇函数，为奇函数，则_________.
四、双空题
16、若数列满足，则称数列为牛顿数列.如果，数列为牛顿数列，设，且，则_________；数列的前n项和为，则_________.
五、解答题
17、已知函数.
(1)求的最小正周期；
(2)将的图象先向右平移个单位，再将图象上所有点的横坐标缩短为原来的倍（纵坐标不变），得到函数的图象，求的对称轴.
18、已知数列是等差数列，数列是各项均为正数的等比数列，其前n项和为，且有，，.
(1)求数列，的通项公式；
(2)令，数列的前11项和.
19、在中，内角A，B，C所对的边分别为a，b，c，且.
(1)证明：；
(2)若，求B.
20、已知三次函数.
(1)当时，求曲线在点处的切线方程，
(2)讨论的单调性.
21、设正项数列满足，且.
(1)证明：数列是等差数列，并求数列的通项公式；
(2)设，求证：数列的前项和.
22、已知函数.
(1)若，恒成立，求a的取值范围；
(2)证明：对任意，；
(3)讨论函数零点的个数.
参考答案
1、答案：A
解析：得：，
所以，
所以.
故选：A.
2、答案：C
解析：充分性：由得，
故，则，故A，B，C三点共线，所以充分性成立，
必要性：若A，B，C三点共线，由共线向量定理可知，
从而，所以，
所以，所以必要性成立.
综上所述：”是“A，B，C三点共线”的充要条件.
故选：C.
3、答案：B
解析：因为是等比数列，
所以，
故，得.
故选：B.
4、答案：D
解析：且四边形四条边长分别为3，4，5，6，
，
，
当，即时，
故选：D.
5、答案：B
解析：由，且，
解得：或，
又因为为第三象限角，所以，，
所以.
所以.
故选：B.
6、答案：A
解析：因为，所以，
令，得；令，得；
所以在上单调递增，在上单调递减，
故的极大值点为，且，
令，则，得，且，
即在R上有唯一大于0的零点.
对于B，其图象的极大值点为，矛盾，故B错误；
对于C，其图象先减后增，矛盾，故C错误；
对于D，其图象有两个零点，矛盾，故D错误；
对于A，其图象满足上述结论，又排除了BCD，故A正确.
故选：A.
7、答案：C
解析：记的中点为D，连结，，如图，
因为点O为的外心，D为的中点，所以，则，
所以
.
故选：C.
8、答案：B
解析：方法一：由得，由得，
因为方程的根为p，
所以函数与的图象交点P的横坐标为p，
同理：函数与的图象交点Q的横坐标为q，
因为与互为反函数，所以两函数图象关于对称，
易知直线与直线互相垂直，所以P，Q两点关于直线对称，
即P，Q的中点M一定落在，亦即点M为与的交点，
联立，解得，即，
所以，
故，则，
令，得；令，得；
所以在上单调递减，在上单调递增，所以，
而，，，
则，，
令，则，
所以在上单调递增，
所以，即，
故，令，则，
令，得，所以在上单调递增，
所以
，
则，故，
综上：.
故选：B.
方法二：前面部分同方法一得，，
则，令，得；令，得；
所以在上单调递减，在上单调递增，所以，
而，，，
因为，当且仅当时取等号，所以，
当时，，
所以，
即，下面比较，的大小关系，
设，，
所以，
故在上递增，，即有，
亦即，综上：.
故选：B.
9、答案：AC
解析：因为，
所以，即，
对于A，当时，，故A正确；
对于B，当时，，故B错误；
对于C，当时，，故C正确；
对于D，当时，，故D错误.
故选：AC.
10、答案：ACD
解析：对于A，数列为等差数列，，，
数列为递减的等差数列，，，故A正确，
对于B，数列为递减的等差数列，，，
的最大值为，故B错，对于C，，，
由得，，
，的最小值为，即，故C正确，
对于D，，故D正确.
故选：ACD.
11、答案：BCD
解析：由，，，得：
对A，，
当且仅当，时取等，故A错误；
对B，，时取等，
两边平方可得，故B正确；
对C，由柯西不等式可得：
，
取等，故C正确；
对D，由，时取等，
所以成立，故D正确.
故选：BCD.
12、答案：BCD
解析：对于A，因为，
所以，
则由正弦定理得
，
则，
因为，所以，故，
又，所以，故A错误；
对于B，由余弦定理得，
因为，即，代入上式得：
，
整理得，解得或（舍去），则，
所以，故B正确；
对于C，设，，边上的高分别是，，，
则由三角形面积公式易得，，，
则，
此时，得，所以，
又，当且仅当时等号成立，
所以，故C正确；
对于D，因为，所以
，
可得，
整理得，故，
所以，
当且仅当且，即时，等号成立，
所以，即的最小值为，故D正确.
故选：BCD.
13、答案：或
解析：因为，，所以，则，
又因为，，
由平面向量的数量积公式可知：，
所以与夹角的余弦值为.
故答案为：.
14、答案：
解析：因为在R上单调递增，
所以当时，在上单调递增，
故，且，
当时，在上单调递增，故，且，
所以，解得或，
由于上述条件要同时成立，所以或，
故a的取值范围为.
故答案为：.
15、答案：68
解析：而是定义域为R的奇函数，故有，且，
因为为奇函数，所以，
而，
所以，
用替换x得：，
令，则有，
即；
令，则，
则，即；
令，则有；
所以.
；
；
；
所以
.
故答案为：68.
16、答案：；
解析：①因为，所以，
，
则，，
则有，
则，
所以是以为首项，公比为2的等比数列，
所以，所以，
解得：.
②，所以.
故答案为：；.
17、答案：(1)π
(2)，
解析：（1），
故的最小正周期.
（2）的图象先向右平移个单位得到：
的图象；
再将图象上所有点的横坐标缩短为原来的倍（纵坐标不变）得到：
的图象；
令，，解得，，
故的对称轴为，.
18、答案：(1)，
(2)748
解析：（1）设等差数列的公差为d，
各项均为正数的等比数列的公比为，
由得：，
，，
解得：，，
（2）由（1）知，
.
19、答案：(1)证明见详解
(2)
解析：（1）证明：因为，
所以，又，
，
即，
又，且A，B为三角形内角，，
则，即.
（2）由（1）知，，
由正弦定理可得，.
根据余弦定理可知，，，
联立可得，.
又，则，所以，则，
则，
又，则.
20、答案：(1)
(2)见解析
解析：（1）当时，，
，
所以曲线在点处的切线斜率为，
又，，
整理可得曲线在点处的切线方程为.
（2），
若，由可得，
当时，，为增函数，
当时，，为减函数，
当时，，
可得或，
所以在，为增函数，在上为减函数，
当时，若，
在，为减函数，在上为增函数，
若，，在R上为减函数，
若，在,为减函数，在上为增函数，
综上可得：若，
在上为增函数，在上为减函数，
当时，在，为增函数，在上为减函数，
当时，若，
在，为减函数，在上为增函数，
若，，在R上为减函数，
若，在，为减函数，在上为增函数.
21、答案：(1)证明见解析；
(2)证明见解析
解析：（1）因为，
所以，又，故，
所以是首项为1，公差为1的等差数列，
故，则，
因为数列是正项数列，所以.
（2）由（1）得，
当时，；
当时，，
所以.
综上：.
22、答案：(1)
(2)见详解
(3)时，有一个零点，时，有三个零点
解析：（1）求导可得：，
若，对任意的，，为减函数，
所以，符合题意；
若，考查函数，
当，即时，，此时在上为减函数，
有，符合题意；
当，即时，令可得：
，，
所以，当时，，为增函数，
所以，不符题意，
综上可得：a的取值范围为.
（2）由（1）知当时，成立，
即时，恒有，
即当时，成立.
取（），有，
即，1，2，3，…，n，
所以，，，…，
，
将上述不等式相加可得：，
整理可得，
即，成立.
（3）由（），
当时，，为减函数，
又，，
此时在内有一个零点；
当时，令，可得或（舍），
此时有一个零点，
当时，考查函数，
若，即时，，
所以为减函数，由，
，此时有一个零点在内；
若，时，有两解，
，，，
此时在，上为减函数，在上为增函数，
由可知，所以极小值，极大值，
由，取，，
令，，
令，则，
由所以，所以为减函数，
所以，所以为减函数，
所以，所以，
可得，此时有三个零点，
综上可得：时，有一个零点，时，有三个零点.