人教版九年级下册28.1 锐角三角函数学案

这是一份人教版九年级下册28.1 锐角三角函数学案，共6页。学案主要包含了旧知回顾，新知梳理，试一试，拓展延伸等内容，欢迎下载使用。
班级： 姓名： 组号：
正弦
一、旧知回顾
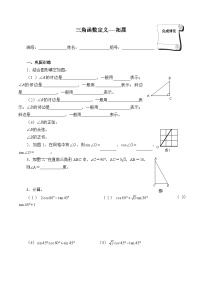
1．如图1在RT△ABC中，斜边是 ，∠A的对边 。
2．如图1，在Rt△ABC中，∠C=90°，∠A=30°，AB=4，则BC= 。根据什么？ 。
3．如图2Rt△ABC与Rt△A'B'C'，∠C=∠C'=90º，∠A=∠A'，求证：。

图2
认真阅读课本61-63页内容并完成下列问题！
二、新知梳理
4．（1）问题为了绿化荒山，市绿化办打算从位于山脚下的机井房沿着山坡铺设水管，对坡面的绿地进行喷灌。现测得斜坡与水平面所成角的度数是30°，为使出水口的高度为25m，那么需要准备多长的水管？
（2）在上面的问题中，如果使出水口的高度为40m，那么需要准备多长的水管？
（3）根据以上的两个问题你发现了什么？
5．如图3，任意画一个Rt△ABC，使∠C＝90°，∠A＝45°，计算∠A的对边与斜边的比(即) ，你能得出什么结论？
图3
6．如图4，任意画Rt△ABC和Rt△A'B'C'，使得∠C＝∠C'＝90.∠A＝∠A'＝α，那么与有什么关系。你能解释一下吗？
图4
归纳：正弦的概念及表示(结合图5)
图5
三、试一试
认真阅读课本P63的例1完成下列题目（注意解题格式）
7．在Rt中，。
= 1 \* GB3 ①图6（1）求值。
= 2 \* GB3 ②图6（2）求的值。
图6

一、课堂活动、记录
1．结合图形理解正弦的定义。
2．怎样求一个锐角的正弦值。
3．求正弦的前提条件是什么？
二、精练反馈
A组
1．在Rt△ABC中，∠C=90°，a=1，c=4，则sinA的值是（ ）。
2．在Rt中，，，，则sinA=
B组
图7
3．如图7，已知∠D=90°，，，，，求。
4．课后思考：类比正弦，当锐角A的大小确定时，∠A的邻边与斜边的比，∠A的对边与邻边的比也是确定的吗？
三、课堂小结
1．什么是一个角的正弦？如何表示？
2．怎样求一个角的正弦？
3．你的其他收获。
图8
四、拓展延伸（选做题）
1．如图8，已知点P的坐标是（a，b），则sinα等于（ ）
A． B． C．
2．如图9，在RT△ABC中，∠ACB=90°，CD⊥AB，点D为垂直，已知AC=8，BC=6。
（1）求sinA的值；（2）求CD的长；（3）求sin∠BCD的值。

图9
【答案】
【学前准备】
旧知回顾
1．AB；BC
2．2；30°角所对的直角边等于斜边的一半
3．解：Rt△ABC与Rt△A'B'C'中
∠C=∠C'=90º，∠A=∠A'
△ABC∽△A'B'C'
新知梳理
4．（1）答：50m
（2）答：80m
（3）发现：在直角三角形中，30°角的对边与斜边的比值不变
5．结论：在直角三角形中，45°角的对边与斜边的比值不变，都是
6．答：=
在Rt△ABC与Rt△A'B'C'中
∠C=∠C'=90º，∠A=∠A’
△ABC∽△A'B'C'
归纳：答：在Rt△ABC中，∠C=90°，我们把锐角A的对边与斜边的比叫做∠A的正弦，
记作sinA，即sinA= =
7．①解：在Rt△ABC中，，BC=6，AC=8，
AB=10，sinA===
②解：在Rt△ABC中，，，BC=1，AB=2；
AC=，sinB ==
【课堂探究】
课堂活动、记录
略
精练反馈
1．A
2．
3．解：在Rt△BCD中
BC=
又
，即是直角三角形
sinB=
4．略
课堂小结
略
拓展延伸
1．D
2．解：（1）因为∠ACB=90°由勾股定理得 AB²=AC²+BC²=8²+6²
AB=10
（2）CD⊥AB于点D 所以S△ABC=1/2*AC*BC=1/2*AB*CD
所以
CD=AC*BC/AB=8×6÷10=4.8
（3）