中职数学高教版（中职）基础模块上册(2021)2.3 一元二次不等式背景图课件ppt

这是一份中职数学高教版（中职）基础模块上册(2021)2.3 一元二次不等式背景图课件ppt，文件包含23一元二次不等式课件pptx、23一元二次不等式教案pdf等2份课件配套教学资源，其中PPT共28页， 欢迎下载使用。

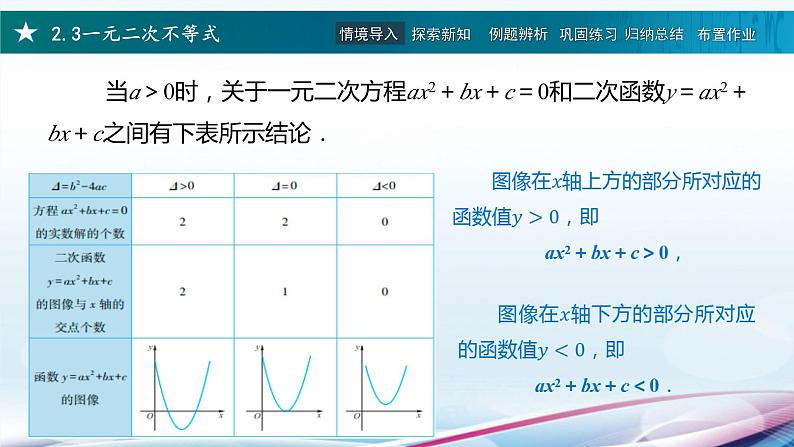
当a＞0时，关于一元二次方程ax2＋bx＋c＝0和二次函数y＝ax2＋bx＋c之间有下表所示结论．
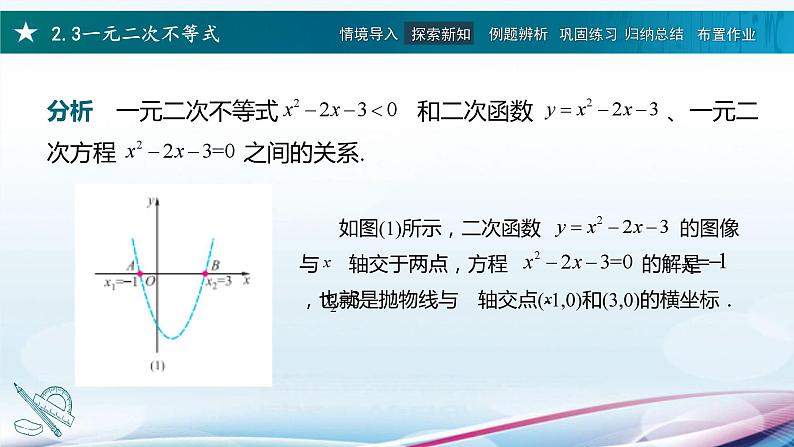
一元二次不等式与一元二次方程、二次函数形式上很接近，关系很密切，我们是能否借助它们之间的关系求解形如 ax2＋bx＋c＜0或ax2＋bx＋c＞0这样的一元二次不等式呢？
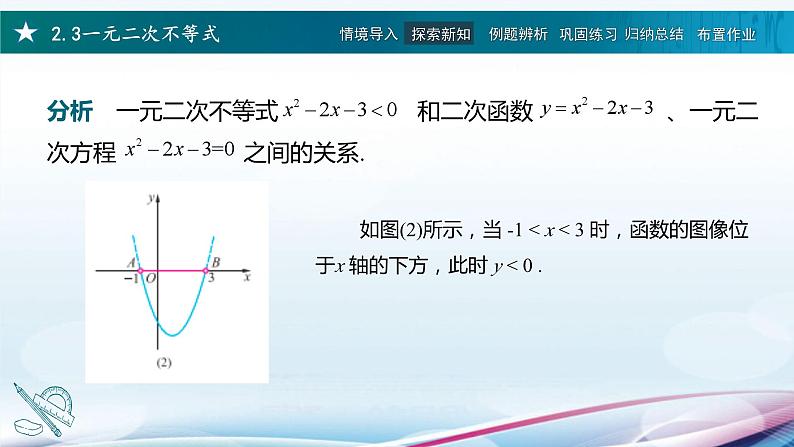
如图(2)所示，当 -1 < x < 3 时，函数的图像位于x 轴的下方，此时 y < 0 .
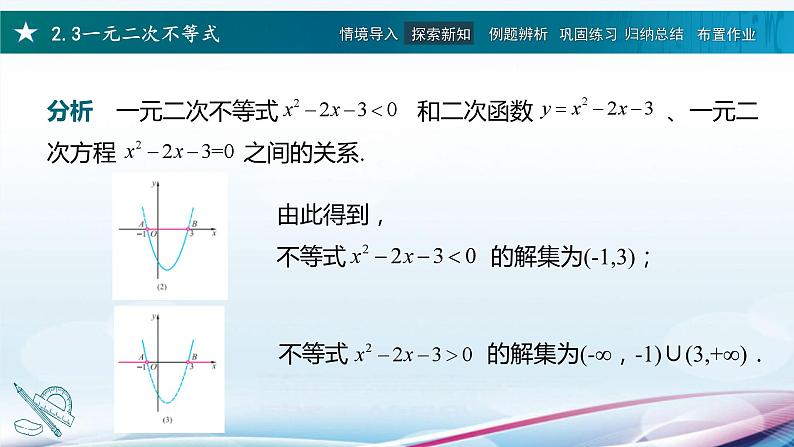
如图(3)所示，当 x<-1 或 x>3 时，函数的图像位于 x 轴的上方，此时 y>0 .
先求出一元二次方程的根，再根据二次函数图象与x轴的相关位置确定一元二次不等式的解集．
按照上面的分析，可以得到一般的一元二次不等式ax2＋bx＋c＞0 ( a>0 )和 ax2＋bx＋c<0 ( a>0 )的求解方法：
例1 求下列一元二次不等式的解集：
当二次项系数a＜0时，由不等式的性质，不等式两边同乘−1，不等号方向改变，就可以将a＜0的情形转化为a＞0的情形，得到与原不等式同解的不等式，然后求解即可．
1.书面作业：完成课后习题和学习与训练；2.查漏补缺：根据个人情况对课题学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.