数学基础模块 下册单元小结评优课课件ppt

这是一份数学基础模块 下册单元小结评优课课件ppt，文件包含中职数学北师大版基础模块下册第六章《直线与圆》单元小结课件pptx、中职数学北师大版基础模块下册第六章《直线与圆的方程》单元小结教学设计docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

第六单元 直线与圆的方程 单元小结
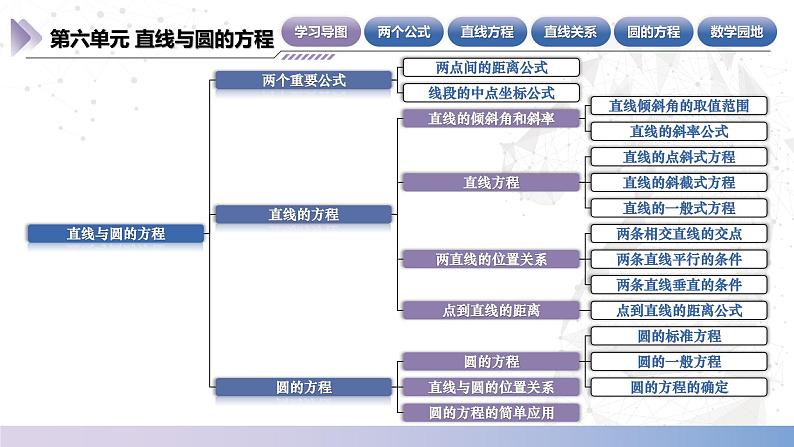
第六章 直线与圆的方程
第六单元 直线与圆的方程
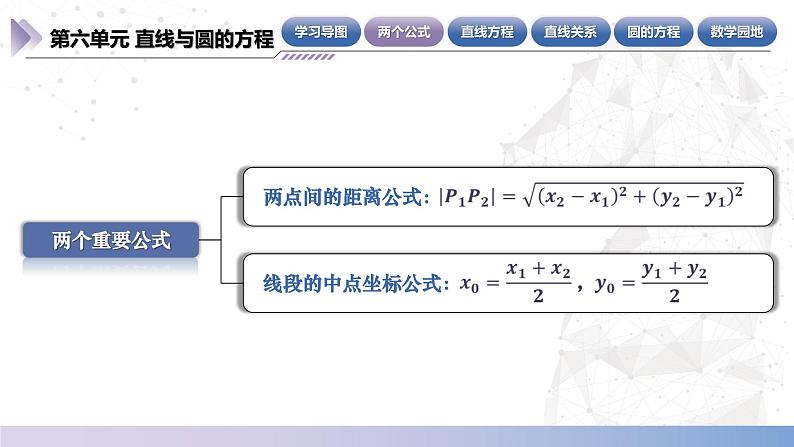
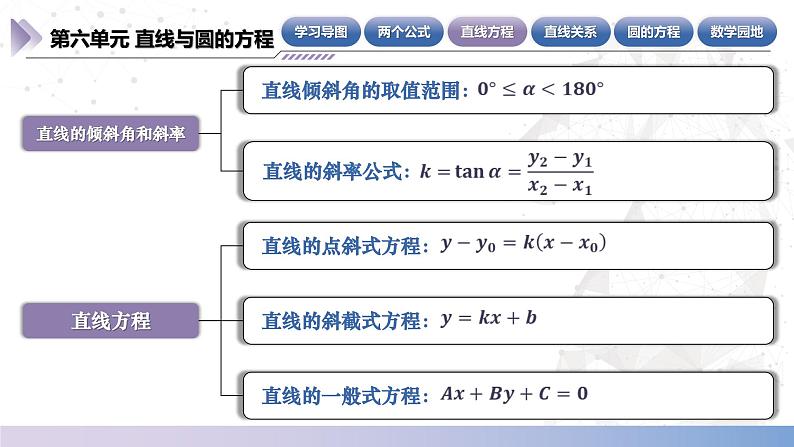
1.直线的倾斜角和斜率
4.关于点到直线的距离
6.关于直线与圆的位置关系
“数缺形时少直观，形缺数时难入微。”正是解析几何将数与形联系在了一起，在“代数”和“几何”两大学科之间架起了桥梁。这座桥梁的设计师就是笛卡尔（Descartes，1596-1650）。
笛卡尔1596年出生于法国，从小学习数学、物理、哲学，成绩优异，笛卡尔22岁时轻易解决了当时的有奖数学难题，这使他对数学产生了兴趣，并坚定了投身于数学研究的信心。在之后的研究中，他不断地思考数学、哲学上的新方法——怎样把代数应用到几何中，并致力于研究数学中这一崭新的领域，这一领域后来被牛顿称为解析几何。
解析几何产生之前，几何就是单纯的研究图形的学问，而代数是用来研究方程的。二者没有任何联系，传统的几何过于抽象，过多地依赖于图形，以至于“它只能使人在想象力大大疲乏的情况下，去练习理解力”，而传统的代数也存在过多地依赖法则和公式的问题，以至于“成为一种充满混杂与晦暗、故意用来阻碍思想的艺术，而不像一门改进思想的科学”。笛卡尔主张采取代数和几何中一切最好的东西，互相以长补短。
笛卡尔的思想方法的精髓是引进坐标，用代数方程表示曲线，然后通过对方程的讨论研究曲线的性质。这样巧妙地把“数”和“形”统一起来，使几何中的点与代数中的有序实数对之间建立了对应关系，这对于数学研究来说具有划时代的意义。
正如笛卡尔所说的：“一切问题都可以转化为数学问题，一切数学问题都可以转化为代数问题，而一切代数问题都可转化为方程，因此，一旦解决了方程问题，一切问题都将迎刃而解。”