第1章 全等三角形（单元测试·培优卷）-2023-2024学年八年级数学上册专题讲与练（苏科版）

这是一份第1章 全等三角形（单元测试·培优卷）-2023-2024学年八年级数学上册专题讲与练（苏科版），共27页。试卷主要包含了单选题，解答题等内容，欢迎下载使用。
1．下列图标中，不是由全等图形组合成的是（ ）
A． B． C． D．
2．已知与全等，A、B、C的对应点分别为D、E、F，且E点在AE上，B、F、C、D四点共线，如图所示若，，则下列叙述何者正确？（ ）
A．， B．，
C．， D．，
3．如图所示，，，欲证，则可增加的条件是（ ）

A． B． C． D．
4．小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到的水平距离、分别为和，．爸爸在C处接住小丽时，小丽距离地面的高度是（ ）

A． B． C． D．
5．如图，正方形的顶点在直线上，将直线向上平移线段的长得到直线，直线分别交，于点，．若求的周长，则只需知道( )
A．的长 B．的长 C．的长 D．DF的长
6．如图，在中，已知是边上的高线，平分，交于点，，，则的面积等于（ ）
A． B． C． D．
7．如图，已知，小明按如下步骤作图：
（1）以点O为圆心，适当长为半径画弧，交OA于D，交OB于点E
（2）分别以点D、E为圆心，大于的长为半径画弧，两弧在的内部相交于点C
（3）画射线OC
根据上述作图步骤，下列结论正确的有（ ）个
①射线OC是的平分线；②点O和点C关于直线DE对称；③射线OC垂直平分线段DE；④.
A．1 B．2 C．3 D．4
8．如图，， ，点在线段上，过点作，且与交于点，则为（ ）
A． B． C． D．
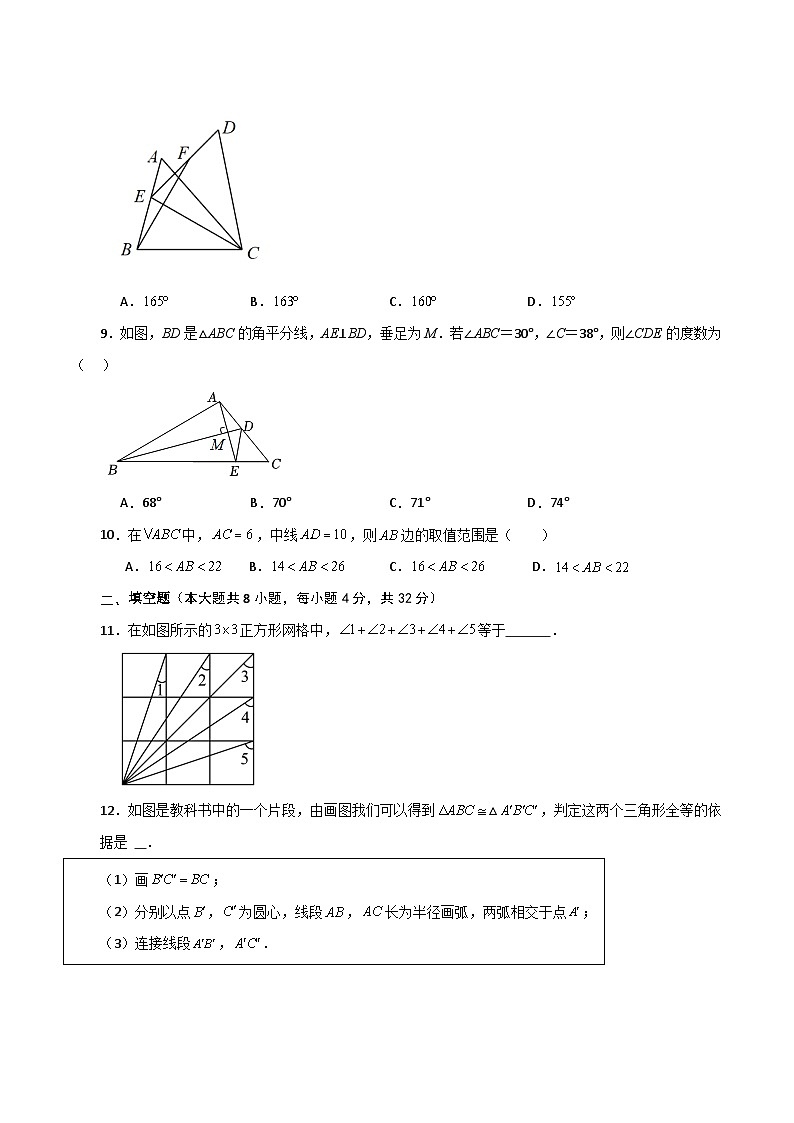
9．如图，BD是△ABC的角平分线，AE⊥BD，垂足为M．若∠ABC＝30°，∠C＝38°，则∠CDE的度数为（ ）
A．68° B．70° C．71° D．74°
10．在中，，中线，则边的取值范围是（ ）
A． B． C． D．
填空题（本大题共8小题，每小题4分，共32分）
11．在如图所示的正方形网格中，等于 ．

12．如图是教科书中的一个片段，由画图我们可以得到△，判定这两个三角形全等的依据是 ．
13．已知，如图，AD=AC，BD=BC，O为AB上一点，那么图中共有 对全等三角形．
14．如图，在中，已知， ，．若，则的度数为 ．
15．如图，在中，，，的平分线与相交于点，过点作交的延长线于点．分别延长 相交于点．判断的数量关系．____.

16．如图，，，为射线，，点P从点B出发沿向点C运动，速度为1个单位/秒，点Q从点C出发沿射线运动，速度为x个单位/秒；若在某时刻，能与全等，则 ．

17．如图，的角平分线、相交于点、若，交于、交于．直接写出、、的数量关系 ．
18．如图，在△ABC中，BD=CD，BE交AD于F，AE=EF，若BE=7CE，，则BF= ．
三、解答题（本大题共6小题，共58分）
19．（8分）已知：如图，，，，相交于点，过点作，垂足为．求证：
(1)．
(2)．
20．（8分）如图，在△ABC和△BDE中，，为锐角，，，连接AE、CD，AE与CD交于点M，AE与BC交于点N．
(1)△ABE与△CBD全等吗？为什么？
(2)AE与CD有何特殊的位置关系，并说明理由．
21．（10分）已知：如图，AC∥BD，AE、BE分别平分∠CAB和∠ABD，点E在CD上．用等式表示线段AB、AC、BD三者之间的数量关系，并证明．
22．（10分）如图，AD是△ABC的高，AD＝BD＝4，E是AD上一点，BE＝AC＝5，S△ABC＝14，BE的延长线交AC于点F．
(1)求证：△BDE≌△ADC；
(2)求证：BE⊥AC；
(3)求EF与AE的长．
23．（10分）如图，在等边三角形中，是边上的动点，以为一边向上作等边三角形，连接．
（1）求证：≌；
（2）求证：；
（3）当点运动到的中点时，与有什么位置关系？并说明理由．
24．（12分）已知：，，，．
（1）试猜想线段与的位置关系，并证明你的结论．
（2）若将沿方向平移至图2情形，其余条件不变，结论还成立吗？请说明理由．
（3）若将沿方向平移至图3情形，其余条件不变，结论还成立吗？请说明理由．
参考答案
1．C
【分析】根据全等图形的概念分析即可．
解：A、该图像是由三个全等的图形构成，故该选项不符合题意；
B、该图像是由五个全等的图形构成，故该选项不符合题意；
C、该图像不是由全等图形构成，故该选项符合题意；
D、该图像是由两个全等的图形构成，故该选项不符合题意；
故选：C．
【点拨】本题考查了全等图形，熟练掌握能够完全重合的两个图形是全等图形是解题的关键．
2．B
【分析】由与全等，A、B、C的对应点分别为D、E、F，可得，，，可得；，可得，由大角对大边可得；利用，可得，即，由上可得正确选项．
解：≌，
，，，
，
．
，，
．
．
，
，即．
．
，．
故选：B．
【点拨】本题主要考查了全等三角形的性质．利用全等三角形对应角相等，对应边相等是解题的关键．
3．D
【分析】根据全等三角形的判定逐一判断即可．
解：由图可知，故A选项不符合题意，
当时，根据不能判定两个三角形全等，故B选项不符合题意，
当时，根据不能判定两个三角形全等，故C选项不符合题意，
当时，
，
∴在和中，
，
，
故选：D．
【点拨】本题考查了全等三角形的判定的应用，注意：全等三角形的判定定理有，，，．
4．D
【分析】利用全等三角形判定，证得与全等，根据全等三角形性质可求出和的值，进而求出的值，最后根据，即可求出问题答案．
解：，
，
，，
，，
，，
又，
，
，，
．
故选：D．
【点拨】本题考查了利用三角形全等测距离的问题，理解题意及熟知三角形的性质与判定是解题关键．
5．A
【分析】过作于，连接，，然后利用已知条件可以证明)，)，接着利用全等三角形的性质即可解决问题．
解：过作于，连接，，
直线向上平移线段的长得到直线，
，
而，，
)，
，
同理)，
，
的周长为：．
求的周长，则只需知道的长．
故选：A．
【点拨】本题主要考查了平移的性质和全等三角形的性质和判定，同时也利用了三角形周长的定义，掌握平移的性质以及全等三角形的性质与判定是解题的关键．
6．A
【分析】作EF⊥BC于F，根据角平分线的性质求得EF=DE=2，然后根据三角形面积公式求得即可．
解：作EF⊥BC于F，
∵BE平分∠ABC，ED⊥AB，EF⊥BC，
∴EF=DE=2，
故选A
【点拨】本题考查了角的平分线的性质以及三角形的面积，作出辅助线求得三角形的高是解题的关键．
7．B
【分析】根据题意可知，，可通过证明三角形全等或线段垂直平分线的判定进行判断.
解：解:连接CD、CE，由作图步骤可知，又，，，射线OC是的平分线，①正确；
连接DE,因为不全等，所以点O和点C关于直线DE不对称，②④错误；
射线OC垂直平分线段DE，③正确.
所以正确的是①③，有2个.

故选B
【点拨】本题考查了角平分线的尺规作图，灵活应用作图步骤所提供的条件是解题的关键.
8．A
【分析】根据全等三角形的性质得出，根据垂直的定义，直角三角形的两锐角互余，得出，根据邻补角即可求解．
解：∵， ，
∴,
∵，
∴,
∴，
故选：A．
【点拨】本题考查了全等三角形的性质，垂直的定义，直角三角形的两锐角互余，邻补角，熟练掌握全等三角形的性质是解题的关键．
9．D
【分析】利用三角形内角和定理求出∠BAC=112°，利用全等三角形的性质证明∠BED=∠BAD即可解决问题．
解：∵∠ABC=30°，∠C=38°，
∴∠BAC=112°，
在△BMA和△BME中，
．
∴△BMA≌△BME（ASA），
∴BA=BE，
在△BDA和△BDE中，
，
∴△BDA≌△BDE（SAS），
∴∠BED=∠BAD=112°，
∴∠CED=68°，
∴∠CDE=180°-∠C-∠CED=74°，
故选：D．
【点拨】本题考查三角形内角和定理，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
10．B
【分析】延长至，使，然后利用“边角边”证明和全等，根据全等三角形对应边相等可得，再利用三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出的取值范围，即为的取值范围．
解：如图，延长至，使，
∵是的中线，
∴，
在和中，
，
∴，
∴，
∵，，
∴，
∴，
即
∴．
故选：B．
【点拨】本题考查全等三角形的判定与性质，三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边．“遇中线，加倍延”构造全等三角形是解题的关键．
11．/225度
【分析】根据图形和正方形的性质可知，，，再把它们相加可得的度数．
解：观察图形可知与所在的三角形全等，二角互余，与所在的三角形全等，二角互余，，
∴，，，
∴．
故答案为：．
【点拨】此题结合网格的特点考查了余角，注意本题中，，是解题的关键．
12．
【分析】根据全等三角形的判定方法解决问题即可．
解：在和△中，
，
，
故答案为：．
【点拨】本题考查了作图−复杂作图，全等三角形的判定等知识，解题的关键是理解题意，灵活应用所学知识解决问题．
13．3
【分析】由已知条件，结合图形可得△ADB≌△ACB，△ACO≌△ADO，△CBO≌△DBO共3对．找寻时要由易到难，逐个验证．
解：∵AD=AC，BD=BC，AB=AB，
∴△ADB≌△ACB；
∴∠CAO=∠DAO，∠CBO=∠DBO，
∵AD=AC，BD=BC，OA=OA，OB=OB
∴△ACO≌△ADO，△CBO≌△DBO．
∴图中共有3对全等三角形．
故答案为3．
14．70°
【分析】（1）证△BED≌△CDF；
（2）利用AB=AC得到∠B与∠C
（3）利用整体法求得∠EDF
解：∵AB=AC，∴∠B=∠C
∵BD=CF，BE=CD
∴△BED≌△CDE，∴∠EDC=∠BED
∵∠A=40°
∴∠B=∠C=70°
∴在△BED中，∠BED+∠BDE=110°
∴∠EDB+∠FDC=110°
∴∠EDF=70°
【点拨】求角度，常见的方法有：
（1）方程思想；
（2）整体思想；
（3）转化思想
本题就是利用全等，结合整体思想求解的角度
15．/0.5
【分析】由，，通过可证，可得，再证明，可得．
解：
在和中
∴；
∴，
∵平分，
∴，
在和中

，
∴；
故答案为：．
【点拨】本题主要考查三角形全等的判定，角平分线的性质，熟练掌握三角形判定定理是解决本题的关键．
16．或
【分析】设运动时间为秒，由题意可知，，，分两种情况讨论：①当时；②当时，利用全等三角形的性质，分别求出的值，即可得到答案．
解：设运动时间为秒，
由题意可知，，，
，
，
①当时，，，
，解得：，
②当时，，，
，解得：，
综上可知，的值为或，
故答案为：或．
【点拨】本题考查了全等三角形的性质，利用分类讨论的思想，熟练掌握全等三角形的性质是解题关键．
17．
【分析】由三角形定理得由角平分线定义得，，在上截取，连接，证明进一步得出，再证明得出，从而可得出结论
解：在中，
∵平分，平分
∴
∴
∴
∴
在上截取，连接
在和中，
∴
∴
在和中，
∴
∵
∴
【点拨】本题主要考查了全等三角形的判定与性质，线段的和与差，正确作出辅助线构造全等三角形是解答本题的关键
18．/
【分析】延长AD至G，使DG＝AD，连接BG，可证明，则BG＝AC，，根据AE＝EF，得到，可证出，即得出AC＝BF，从而得出BF的长．
解：如图，延长AD至G，使DG＝AD，连接BG，
在和中，
∴
∴BG＝AC，，
又∵AE＝EF，
∴，
又∵，
∴，
∴，
∴BG＝BF，
∴AC＝BF，
又∵BE＝7CE，AE＝，
∴BF＋EF＝，
即BF＋＝，
解得BF＝．
故答案为：
【点拨】本题考查了全等三角形的判定和性质，证明线段相等，一般转化为证明三角形全等，正确地作出辅助线构造全等三角形是解题的关键．
19．(1)见解析；(2)见解析
【分析】（1）利用证明；
（2）根据全等三角形的性质得出，则，根据等腰三角形的性质可得出结论．
解：（1）证明：在和中，
，
∴
（2）证明：∵
∴，
∴，
∵，
∴．
【点拨】此题考查了全等三角形的判定与性质，利用证明是解题的关键．
20．(1)全等，见解析；(2)AE与CD互相垂直，见解析
【分析】(1)利用“SAS”可判断△ABE≌△CBD；
(2)利用△ABE≌△CBD得到∠BAE=∠BCD，再根据三角形内角和得到∠NMC=∠ABN=90°，即可判断AE⊥CD
解：△ABE与△CBD全等；
理由如下：
，
，即，
在和△CBD中，

；
（2）解：AE与CD互相垂直；
理由如下：
，
，
，
，
．
【点拨】本题考查了三角形全等的性质与判定，三角形内角和定理，熟悉以上定理是解题的关键．
21．AC+BD=AB，理由见见解析
【分析】在BA上截取BF=BD，连接EF，先证得，可得到∠BFE=∠D，再由AC∥BD，可得∠AFE=∠C，从而证得，可得AF=AC，即可求解．
解：AC+BD=AB，证明如下：
在BA上截取BF=BD，连接EF，如图所示：
∵AE、BE分别平分∠CAB和∠ABD，
∴∠EAF=∠EAC，∠EBF=∠EBD，
在△BEF和△BED中，
，
∴（SAS），
∴∠BFE=∠D，
∵AC∥BD，
∴∠C+∠D=180°，
∵∠AFE+∠BFE=180°，
∴∠AFE+∠D=180°，
∴∠AFE=∠C，
在△AEF和△AEC中，
，
∴（AAS），
∴AF=AC，
∵AF+BF=AB，
∴AC+BD=AB．
【点拨】本题主要考查了全等三角形的判定和性质，熟练掌握全等三角形的判定和性质定理是解题的关键．
22．(1)证明见解析；(2)证明见解析；(3)EF＝，AE＝1．
【分析】（1）利用直角三角形的判定定理证明即可；
（2）利用全等三角形的性质证明∠EBD＝∠CAD，再利用对顶角相等证明∠BED＝∠AEF，进一步可证明∠AFE＝∠ADB＝90°，即BE⊥AC；
（3）利用三角形面积求出BC＝7，进一步求出CD＝3，利用，
证明ED＝CD＝3，进一步求出AE＝AD－ED＝4－3＝1，再利用三角形面积求出BF＝，即可求出EF＝BF－BE＝－5＝．
解：（1）证明：∵AD是△ABC的高，
∴∠ADB＝∠ADC＝90°，
在Rt△BDE和Rt△ADC中，
，
∴．
（2）证明：∵，
∴∠EBD＝∠CAD，
∵∠BED＝∠AEF，
∴∠AFE＝∠ADB＝90°，
∴BE⊥AC．
（3）解：∵S△ABC＝AD•BC＝14，AD＝4，
∴BC＝7，
∵BD＝4，
∴CD＝3，
∵，
∴ED＝CD＝3，
∴AE＝AD－ED＝4－3＝1，
∵S△ABC＝BF•AC＝14，BE＝AC＝5，
∴BF＝，
∴EF＝BF－BE＝－5＝．
【点拨】本题考查全等三角形的判定及性质，对顶角相等，垂直的定义，解题的关键是掌握全等三角形的判定及性质．
23．（1）见解析；（2）见解析；（3），见解析．
【分析】（1）根据和是等边三角形，得到边角关系，即，，，根据等式性质得到，最后利用证明全等即可；
（2）根据≌，可知对应角，又因为，等量代换可知，进而得到；
（3），由是等边三角形，点为的中点，根据三线合一可知，再根据≌，进而得到，最后可求得的度数．
解：（1）和是等边三角形；
，，，
，
即，
在与中
，
≌；
（2）≌，
；
，
，
；
（3），理由如下：
是等边三角形，点为的中点，
，，，
，
，
≌，
，
，
．
【点拨】本题考查了等边三角形的性质和全等三角形的判定和性质，等式的性质以及平行线的判定等知识点，准确的运用这些性质是解题的关键．
24．（1），见解析；（2）成立，理由见解析；（3）成立，理由见解析
【分析】（1）先用判断出，得出，进而判断出，即可得出结论；
（2）同（1）的方法，即可得出结论；
（3）同（1）的方法，即可得出结论．
解：（1）理由如下：
∵，，
∴
在和中
∴，
∴
∵，
∴，
∴，
∴；
（2）成立，理由如下：
∵，，
∴，
在和中，
∴，
∴，
∵，
∴，
∴，
在中，，
∴；
（3）成立，理由如下：
∵，，
∴
在和中，
∴，
∴，
∵，
∴，
在中，，
∴．
【点拨】此题是几何变换综合题，主要考查了全等三角形的判定和性质，直角三角形的性质，判断出是解本题的关键．（1）画；
（2）分别以点，为圆心，线段，长为半径画弧，两弧相交于点；
（3）连接线段，．