2023年初中数学8年级上册同步压轴题 专题02 全等三角形中的六种模型梳理（学生版+教师解析）

这是一份2023年初中数学8年级上册同步压轴题 专题02 全等三角形中的六种模型梳理（学生版+教师解析），文件包含2023年初中数学8年级上册同步压轴题专题02全等三角形中的六种模型梳理教师版含解析docx、2023年初中数学8年级上册同步压轴题专题02全等三角形中的六种模型梳理学生版docx等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。
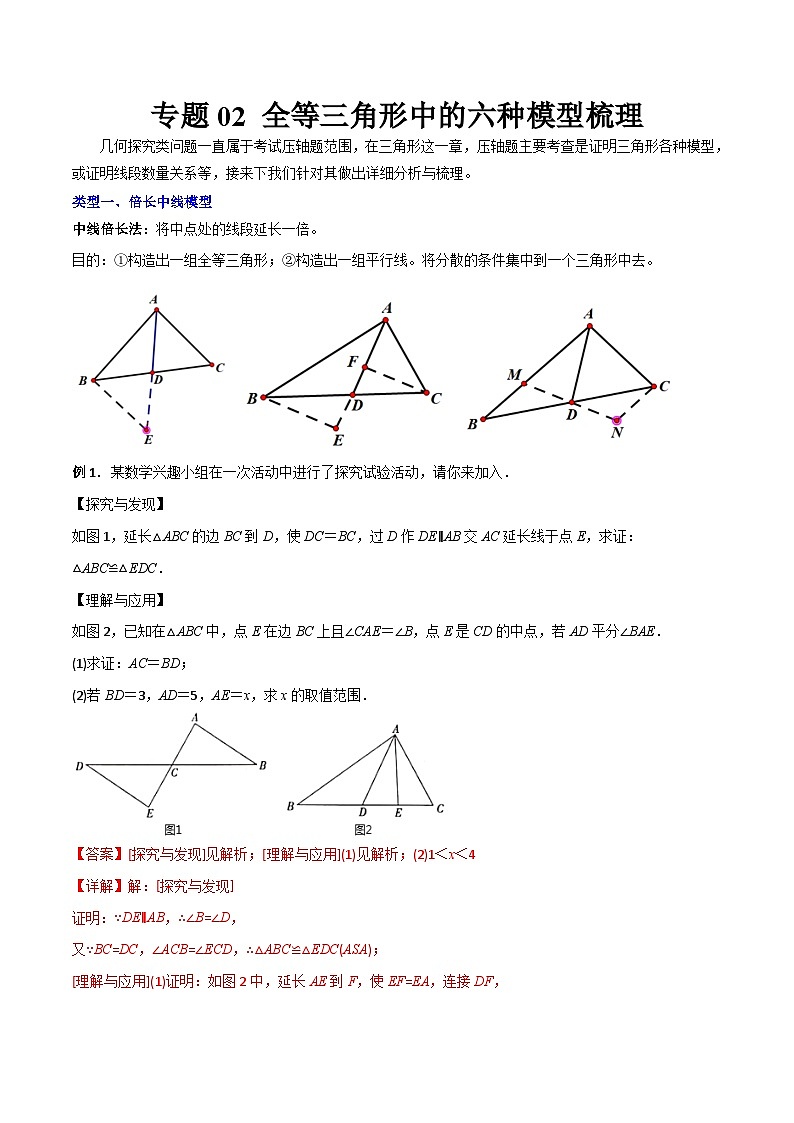
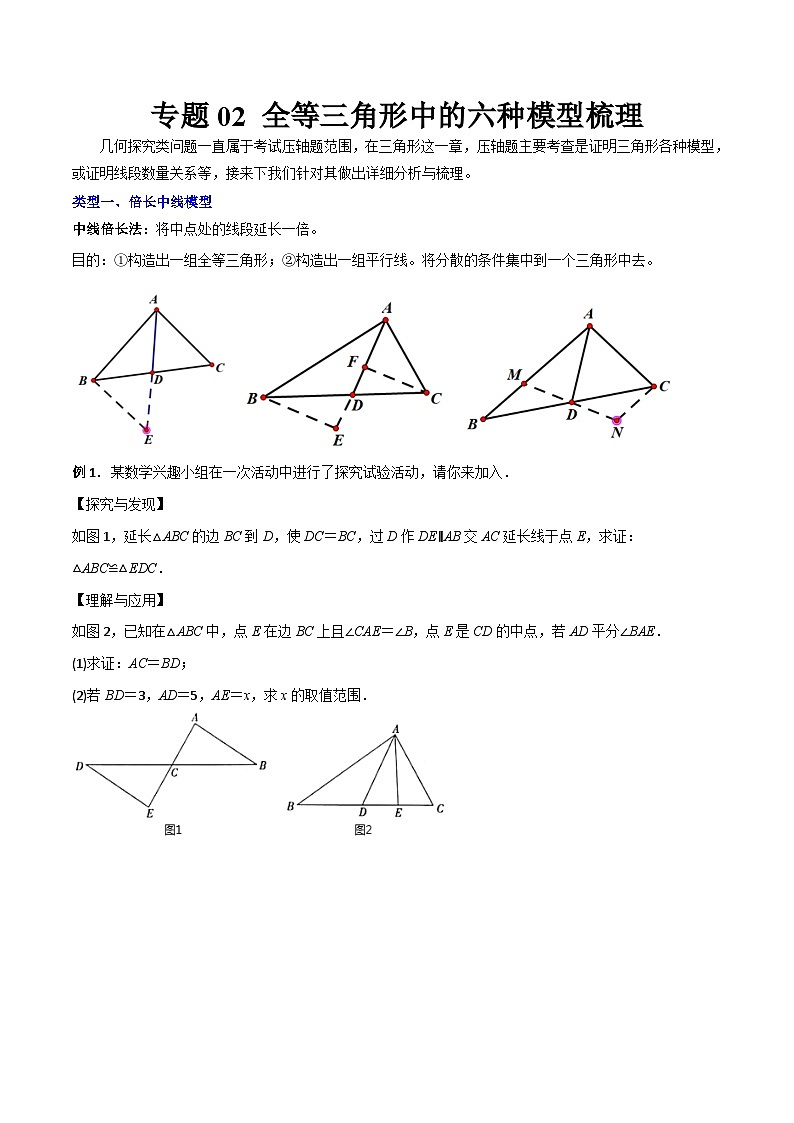
类型一、倍长中线模型
中线倍长法：将中点处的线段延长一倍。
目的： = 1 \* GB3 ①构造出一组全等三角形； = 2 \* GB3 ②构造出一组平行线。将分散的条件集中到一个三角形中去。
例1．某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．
【探究与发现】
如图1，延长△ABC的边BC到D，使DC＝BC，过D作DE∥AB交AC延长线于点E，求证：△ABC≌△EDC．
【理解与应用】
如图2，已知在△ABC中，点E在边BC上且∠CAE＝∠B，点E是CD的中点，若AD平分∠BAE．
(1)求证：AC＝BD；
(2)若BD＝3，AD＝5，AE＝x，求x的取值范围．
【变式训练1】如图1，在中，是边的中线，交延长线于点，．

(1)求证；
(2)如图2，平分交于点，交于点，若，，求的值．
【变式训练2】(1)如图1，已知中，AD是中线，求证：；
(2)如图2，在中，D，E是BC的三等分点，求证：；
(3)如图3，在中，D，E在边BC上，且．求证：．
【变式训练3】在中，点为边中点，直线绕顶点旋转，直线于点．直线于点，连接，．
(1)如图1，若点，在直线的异侧，延长交于点．求证：．
(2)若直线绕点旋转到图2的位置时，点，在直线的同侧，其它条件不变，此时，，，求的长度．
(3)若过点作直线于点．试探究线段、和的关系．
类型二、截长补短模型
截长补短法使用范围：线段和差的证明(往往需证2次全等)
例．在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N，P为△ABC外一点，且∠MPN＝60°，∠BPC＝120°，BP＝CP．探究：当点M、N分别在直线AB、AC上移动时，BM，NC，MN之间的数量关系．
(1)如图①，当点M、N在边AB、AC上，且PM＝PN时，试说明MN＝BM+CN．
(2)如图②，当点M、N在边AB、AC上，且PM≠PN时，MN＝BM+CN还成立吗？
答： ．(请在空格内填“一定成立”“不一定成立”或“一定不成立”)．
(3)如图③，当点M、N分别在边AB、CA的延长线上时，请直接写出BM，NC，MN之间的数量关系．
【变式训练1】如图，在四边形中，，点E、F分别在直线、上，且．
(1)当点E、F分别在边、上时(如图1)，请说明的理由．
(2)当点E、F分别在边、延长线上时(如图2)，(1)中的结论是否仍然成立？若成立，请说明理由；若不成立，请写出、、之间的数量关系，并说明理由．
【变式训练2】(1)阅读理解：问题：如图1，在四边形中，对角线平分，．求证：．
思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题．
方法1：在上截取，连接，得到全等三角形，进而解决问题；
方法2：延长到点，使得，连接，得到全等三角形，进而解决问题．
结合图1，在方法1和方法2中任选一种，添加辅助线并完成证明．
(2)问题解决：如图2，在(1)的条件下，连接，当时，探究线段，，之间的数量关系，并说明理由；
(3)问题拓展：如图3，在四边形中，，，过点D作，垂足为点E，请直接写出线段、、之间的数量关系．
【变式训练3】在中，BE，CD为的角平分线，BE，CD交于点F．
(1)求证：；
(2)已知．
①如图1，若，，求CE的长；
②如图2，若，求的大小．
类型三、做平行线证明全等
例1．如图所示：是等边三角形，、分别是及延长线上的一点，且，连接交于点．
求让：
【变式训练1】 P为等边△ABC的边AB上一点，Q为BC延长线上一点，且PA＝CQ，连PQ交AC边于D．
(1)证明：PD＝DQ．
(2)如图2，过P作PE⊥AC于E，若AB＝6，求DE的长．
【变式训练2】已知在等腰△ABC中，AB=AC，在射线CA上截取线段CE，在射线AB上截取线段BD，连接DE，DE所在直线交直线BC与点M．请探究：
(1)如图(1)，当点E在线段AC上，点D在AB延长线上时，若BD=CE，请判断线段MD和线段ME的数量关系，并证明你的结论．
(2)如图(2)，当点E在CA的延长线上，点D在AB的延长线上时，若BD=CE，则(1)中的结论还成立吗？如果成立，请证明；如果不成立，说明理由；
类型四、旋转模型
例．如图1，，，，、相交于点，连接．
(1)求证：，并用含的式子表示的度数；
(2)当时，取，的中点分别为点、，连接，，，如图2，判断的形状，并加以证明．
【变式训练1】四边形是由等边和顶角为的等腰排成，将一个角顶点放在处，将角绕点旋转，该交两边分别交直线、于、，交直线于、两点．
(1)当、都在线段上时(如图1)，请证明：；
(2)当点在边的延长线上时(如图2)，请你写出线段，和之间的数量关系，并证明你的结论；
(3)在(1)的条件下，若，，请直接写出的长为 ．
【变式训练2】(1)问题发现：
如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．则：
①∠AEB的度数为 °；
②线段AD、BE之间的数量关系是 ．
(2)拓展研究：
如图2，△ACB和△DCE均为等腰三角形，且∠ACB＝∠DCE＝90°，点 A、D、E在同一直线上，若AD＝a，AE＝b，AB＝c，求a、b、c之间的数量关系．
(3)探究发现：
图1中的△ACB和△DCE，在△DCE旋转过程中，当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．
【变式训练3】如图1，在中，，，点，分别在边，上，，连接，点，，分别为，，的中点．
(1)观察猜想：图1中，线段与的数量关系是______，位置关系是______．
(2)探究证明：把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由；
(3)拓展延伸：把绕点在平面内自由旋转，若，，请直接写出面积的最大值．
类型五、手拉手模型
例．在等边中，点D在AB上，点E在BC上，将线段DE绕点D逆时针旋转60°得到线段DF，连接CF．
(1)如图(1)，点D是AB的中点，点E与点C重合，连接AF．若，求AF的长；
(2)如图(2)，点G在AC上且，求证：；
(3)如图(3)，，，连接AF．过点F作AF的垂线交AC于点P，连接BP、DP．将沿着BP翻折得到，连接QC．当的周长最小时，直接写出的面积．
【变式训练1】△ACB和△DCE是共顶点C的两个大小不一样的等边三角形．
(1)问题发现：
如图1，若点A，D，E在同一直线上，连接AE，BE．
①求证：△ACD≌△BCE；②求∠AEB的度数．
(2)类比探究：如图2，点B、D、E在同一直线上，连接AE，AD，BE，CM为△DCE中DE边上的高，请求∠ADB的度数及线段DB，AD，DM之间的数量关系，并说明理由．
(3)拓展延伸：如图3，若设AD(或其延长线)与BE的所夹锐角为α，则你认为α为多少度，并证明．
【变式训练2】(1)如图1，锐角△ABC中，分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD＝90°，连接BD，CE，试猜想BD与CE的大小关系，不需要证明．
【深入探究】(2)如图2，四边形ABCD中，AB＝5，BC＝2，∠ABC＝∠ACD＝∠ADC＝45°，求BD2的值；甲同学受到第一问的启发构造了如图所示的一个和△ABD全等的三角形，将BD进行转化再计算，请你准确的叙述辅助线的作法，再计算；
【变式思考】(3)如图3，四边形ABCD中，AB＝BC，∠ABC＝60°，∠ADC＝30°，AD＝6，BD＝10，则CD＝ ．
【变式训练3】(1)问题发现：
如图1，和均为等腰直角三角形，，连接，，点、、在同一条直线上，则的度数为__________，线段、之间的数量关系__________；
(2)拓展探究：
如图2，和均为等腰直角三角形，，连接，，点、、不在一条直线上，请判断线段、之间的数量关系和位置关系，并说明理由．
(3)解决问题：
如图3，和均为等腰三角形，，则直线和的夹角为__________．(请用含的式子表示)
类型六、一线三角模型
例.在中，，，直线MN经过点C且于D，于E．
(1)当直线MN绕点C旋转到图1的位置时，求证：
①≌；
②；
(2)当直线MN烧点C旋转到图2的位置时，求证：；
(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
【变式训练1】【问题解决】
(1)已知△ABC中，AB=AC，D，A，E三点都在直线l上，且有∠BDA=∠AEC=∠BAC．如图①，当∠BAC=90°时，线段DE，BD，CE的数量关系为：______________；
【类比探究】
(2)如图②，在(1)的条件下，当0°