中职数学高教版（中职）基础模块上册(2021)1.3.1 交集评课ppt课件

这是一份中职数学高教版（中职）基础模块上册(2021)1.3.1 交集评课ppt课件，文件包含13集合的运算课件pptx、13集合的运算教案pdf、13集合的运算docx等3份课件配套教学资源，其中PPT共43页， 欢迎下载使用。

实数之间可以进行运算，如5+2=7,4-3=1, 3×7=21． 类比这些运算，集合之间是否也可以进行运算呢？
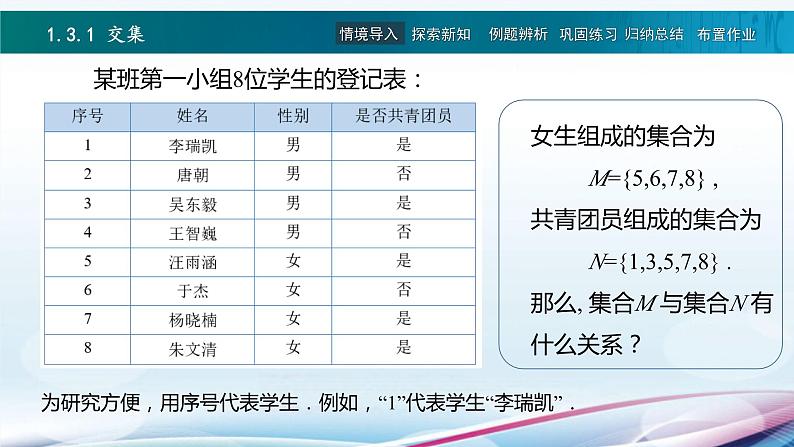
某班第一小组8位学生的登记表：
为研究方便，用序号代表学生．例如，“1”代表学生“李瑞凯”．
一般地,对于给定的集合A与集合B,由既属于集合A又属于集合B的所有元素组成的集合,称为集合A与集合B的交集,记作A∩B.读作“A交B”.即 A∩B={x|x∈A且x∈B}.
“情境与问题”中, 集合S={5,7,8}是集合M={5,6,7,8}与集合N ={1,3,5,7,8}的交集, 即M∩N=S.
两个集合的交集可以用Venn图中的阴影部分表示． 当两个集合没有公共元素时，这两个集合的交集为空集.
例1 设集合A ={2,4,6}, 集合B ={0,1,2}, 求A∩B．
分析 2是集合A与集合B的公共元素.
解 A∩B={2,4,6}∩{0,1,2}={2}．
例2 设集合A={(x,y)| x-y=1}, 集合B={(x,y)|x+y=5},求A∩B．
二元一次方程组的解集是一组有序实数对,可以用列举法表示,也可以用描述法表示.如例2中的解集{(3,2)}的用列举法表示的,也可以用描述法表示为{(x,y)|x =2,y=2}.
例3 设集合A={x| -2分析 将这两个集合在数轴上表示出来，图阴影部分即为两个集合的交集．
解 A∩B={x|-2 由交集的定义可以推知, 对于任何集合A、B, 有(1) A∩B= B∩A ；(2) A∩A=A ；(3) A∩∅=∅∩A=∅ ；(4) A∩B⊆A, A∩B⊆B.
1.设集合A={2,3,4}, 集合B={0,1,2}. 求A∩B．2.设集合A={(x,y)|x-2y=1}, 集合B={(x,y)|x+2y=3}, 求A∩B．3.设集合A ={x |x>-1}, 集合A ={x |x≤-2}, 求A∩B．
前面的同学登记表中,设集合T={1,3,5,6,7,8}.集合T表示的是哪些同学组成的集合呢？这个集合的元素与女生组成的集合M={5,6,7,8}和共青团员组成的集合N={1,3,5,7,8}有什么关系呢？
一般地,对于给定的集合A与集合B,由集合A与集合B的所有元素组成的集合称为集合A与集合B的并集,记作A∪B.读作“A并B”.即 A∪B={x|x∈A或x∈B}.
“情境与问题”中, 集合T={1,3,5,6,7,8}是集合M={5,6,7,8}与集合N ={1,3,5,7,8}的并集, 即M∪N=T.
两个集合的并集可以用Venn图中的阴影部分表示．
例4 设集合A ={1,3,5,7}, 集合B ={0,2,3,4,6}, 求A∪B．
解 A∪B={1,3,5,7}∪{0,2,3,4,6}={0,1,2,3,4,5,6,7}．
求集合的并集时,相同的元素不能重复出现. 例如,例4中集合A 和集合B中都有元素3,但是在A∪B中元素3只出现一次．
例5 设集合A={x|-1分析 将这两个集合在数轴上表示出来，图中阴影部分即为两个集合的并集．
解 A∪B={x |-1 由并集的定义可以推知, 对于任何集合A、B, 有(1) A∪B= B∪A ；(2) A∪A= A ；(3) A∪∅=∅∪A=A ；(4) A⊆A∪B, B⊆A∪B.
1.设集合A={2,3,4}, 集合B={0,1,4}. 求A∪B．2.设集合A ={x |x≥-1}, 集合A ={x |x≤2}，求A∪B．3.设集合A={奇数}, 集合B={偶数}. 求A∪B．4.试给出集合A与集合B, 使A∪B= B.
前面的同学登记表中, 设第一小组所有8名学生组成集合为U={1,2,3,4,5,6,7,8}.那么, 集合U分别与由共青团员组成的集合 {1,3,5,7,8}、由不是共青团员的学生组成的集合E={2,4,6}有什么关系？
研究某些集合时,如果这些集合是一个给定集合的子集,那么这个给定的集合称为全集,通常用字母U表示.在研究数集时，通常把实数集R作为全集．
“情境与问题”中, 第一小组8名同学组成的集合U={1,2,3,4,5,6,7,8}就是这个问题中给定的全集.
前面的同学登记表中,不是共青团员的学生组成的集合是E={2,4,6}.集合E的元素都属于全集U但不属于共青团员组成的集合N ={1,3,5,7,8}.
一般地，如果集合A是全集U的一个子集，则由集合U中不属于集合A的所有元素组成的集合称为集合A在全集U中的补集，记作∁UA．即 ∁UA={x|x∈U且x∉A}.
“情境与问题”中,不是共青团员的学生组成的集合 E={2,4,6} 就是共青团员组成的集合 N={1,3,5,7,8} 在全集U={1,2,3,4,5,6,7,8}中的补集，即∁UN= E．
集合A在全集U中的补集可以用Venn图中的阴影部分表示．
例6 设全集U={x∈N|x＜7}，集合A={1,2,4,6},求∁UA．
解 因为全集U={x∈N|x＜7}={0,1,2,3,4,5,6}，所以 集合A={1,2,4,6}的补集为 ∁UA={0,3,5}.
例7 设全集U= R，集合A={x|-2≤x＜1}．求∁A．
分析 将集合A在数轴上表示出来, 图中阴影部分即为集合A的补集．
解 ∁UA={x|x＜−2或x≥1}.
用数轴求补集的时候要特别注意端点的取舍.
由补集的定义可以推知, 对于任何集合A, 有(1) A∩∁UA=∅ ；(2) A∪∁UA =U ；(3) ∁U(∁UA)=A.
1. 设全集U={x∈N|x＜5}, 集合A={0}, 求∁UA．2. 设全集U=R, 集合A={x|x＞1} , 求∁ UA3. 设全集U=R, 求∁U Q． 4.已知全集U={三角形}, 集合A={直角三角形},求∁UA．
1.书面作业：完成课后习题和学习与训练；2.查漏补缺：根据个人情况对课题学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.