
数学6.7用相似三角形解决问题习题
展开一、单选题
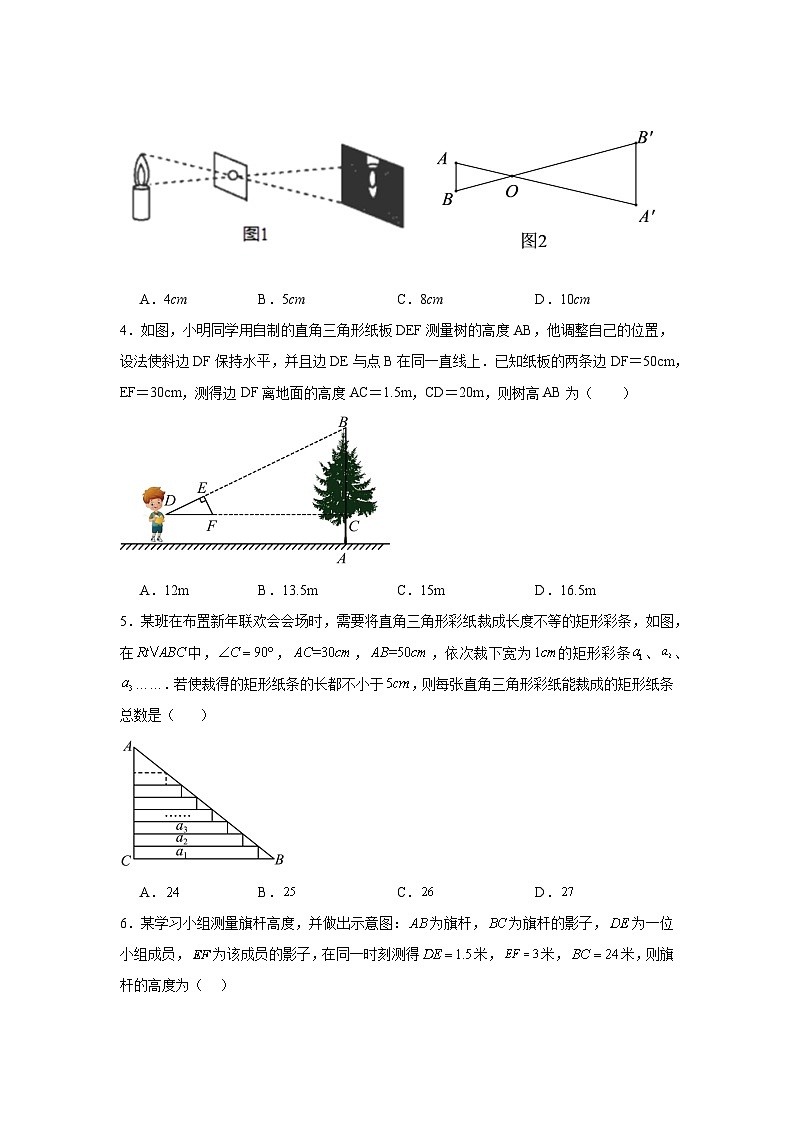
1.古代的“矩”是指包含直角的作图工具,如图1,用“矩”测量远处两点间距离的方法是:把矩按图2平放在地面上,人眼从矩的一端A望点B,使视线刚好通过点E,量出长,即可算得之间的距离.若,,,则( )
A.B.C.D.
2.如图,在中,,,,是斜边上的高,则的长度为( ).
A.B.C.D.
3.如图1,物理课上学习过利用小孔成像说明光的直线传播.现将图1抽象为图2,其中线段AB为蜡烛的火焰,线段A′B′为其倒立的像.如果蜡烛火焰AB的高度为2cm,倒立的像A′B′的高度为5cm,线段OA的长为4cm,那么线段OA′的长为( )
A.4cmB.5cmC.8cmD.10cm
4.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )
A.12mB.13.5mC.15mD.16.5m
5.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图,在中,,,,依次裁下宽为的矩形彩条、、…….若使裁得的矩形纸条的长都不小于,则每张直角三角形彩纸能裁成的矩形纸条总数是( )
A.B.C.D.
6.某学习小组测量旗杆高度,并做出示意图:为旗杆,为旗杆的影子,为一位小组成员,为该成员的影子,在同一时刻测得米,米,米,则旗杆的高度为( )
A.9米B.12米C.15米D.18米
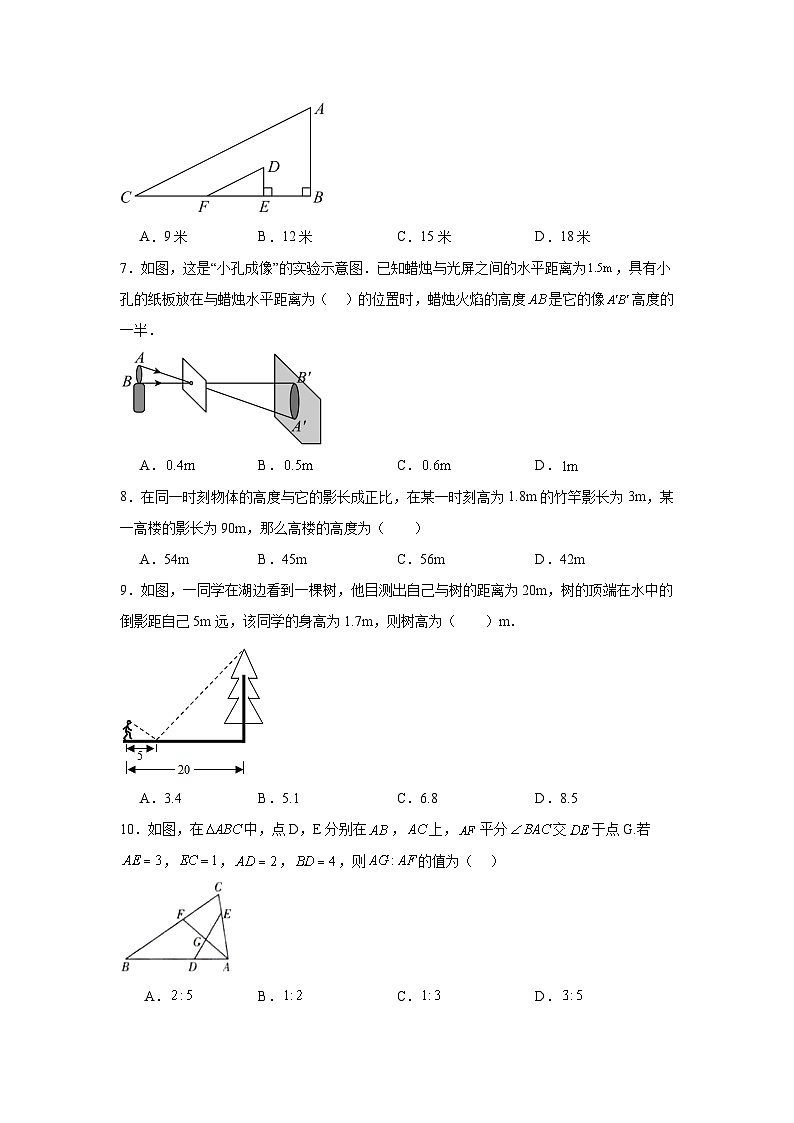
7.如图,这是“小孔成像”的实验示意图.已知蜡烛与光屏之间的水平距离为,具有小孔的纸板放在与蜡烛水平距离为( )的位置时,蜡烛火焰的高度是它的像高度的一半.
A.B.C.D.
8.在同一时刻物体的高度与它的影长成正比,在某一时刻高为1.8m的竹竿影长为3m,某一高楼的影长为90m,那么高楼的高度为( )
A.54mB.45mC.56mD.42m
9.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4B.5.1C.6.8D.8.5
10.如图,在中,点D,E分别在,上,平分交于点G.若,,,,则的值为( )
A.B.C.D.
二、填空题
11.小丽同学想利用树影测量校园内的树高,她在某一时刻测得小树高为1.5m时,其影长为1.2 m,此时她测量教学楼旁的一棵大树影长为5m,那么这棵大树高约 m.
12.如图所示,某校数学兴趣小组利用标杆BE测量某建筑物的高度,已知标杆BE高1.5米,测得AB=1.8米,AC=9米,则建筑物CD的高是 米.
13.如图,小明测得长的竹竿落在地面上的影长为.在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上.他测得这棵树落在地面上的影长为,落在墙面上的影长为,则这棵树的高度是 m.
14.从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的华丽分割线.如图,AC是的华丽分割线,且,若点C的坐标为(2,0),则点A的坐标为 .
15.D、E是△ABC的AB、AC边上的点,DE∥BC, AD=2,DB=3,DE=1,则BC= .
16.一天,小青想利用影子测量校园内一根旗杆的高度,在同一时刻内,小青的影长为米,旗杆的影长为米,若小青的身高为米,则旗杆的高度为 米.
17.两相似三角形的面积之比为9∶16,若小三角形的周长为6厘米,则大三角形的周长为 厘米.
18.在某一时刻测得一根高为1.8m的竹竿的影长为0.9m,如果同时同地测得一栋的影长为27m,那么这栋楼的高度为 m
19.如图,小明在打网球时,她的击球高度AB=2.4米,为使球恰好能过网(网高DC=0.8米),且落在对方区域距网5米的位置P处,则她应站在离网 米处.
20.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 .
三、解答题
21.小明把一个排球打在离他2米远的地上,排球反弹后碰到墙上,如果他跳起来击排球时的高度是1.8米,排球落地点离墙的距离是7米,假设排球一直沿直线运动,那么排球能碰到墙上离地多高的地方?
22.已知,在矩形中,连接对角线,将绕点顺时针旋转得到,并将它沿直线向左平移,直线与交于点,连接,.
(1)如图①,当,点平移到线段上时,线段有怎样的数量关系和位置关系?直接写出你的猜想;
(2)如图②,当,点平移到线段的延长线上时,(1)中的结论是否成立,请说明理由;
(3)如图③,当时,对矩形进行如已知同样的变换操作,线段有怎样的数量关系和位置关系?直接写出你的猜想.
图① 图② 图③
23.如图,小明想用太阳光的照射来测量一大楼的高度.大楼被太阳照射后,其影子投射到与大楼平行的墙面的影子为,小明从大楼向墙面移动,当小明移动到点时,恰好使自己的影子与大楼的影子重叠,且高度相同.此时,测得影子,,(点、、在同一直线上),已知小明身高,请你求出大楼的高度.
24.如图,一路灯AB与墙OP相距20米,当身高CD=1.6米的小亮在离墙17米的D处时,影长DG为1米;当小亮站在点F时,发现自己头顶的影子正好接触到墙的底部O处.
(1)求路灯AB的高度.
(2)请在图中画出小亮EF的位置;并求出此时的影长.
(3)如果小亮继续往前走,在距离墙2米的N处停下,那么小亮MN在墙上的影子有多高?
参考答案:
1.B
2.A
3.D
4.D
5.C
6.B
7.B
8.A
9.B
10.B
11.6.25
12.7.5
13.8
14.或
15.2.5
16.16
17.8
18.54
19.10
20.3
21.
22.(1)AH=CG,AH⊥CG;
AH=CG,AH⊥CG,
AH=nCG,AH⊥CG.
23..
24.(1)6.4米;(2)5米;(3)米
数学苏科版第6章 图形的相似6.7用相似三角形解决问题精品练习题: 这是一份数学苏科版第6章 图形的相似6.7用相似三角形解决问题精品练习题,共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学6.7用相似三角形解决问题巩固练习: 这是一份初中数学6.7用相似三角形解决问题巩固练习,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学苏科版九年级下册6.7用相似三角形解决问题习题: 这是一份初中数学苏科版九年级下册6.7用相似三角形解决问题习题,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













