河南省漯河市召陵区2023-2024学年八年级上学期期中数学试题（含解析）

这是一份河南省漯河市召陵区2023-2024学年八年级上学期期中数学试题（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

（满分120分，时间：100分钟）
一、选择题（每小题3分，共30分）
1．2023年全国民航工作会议介绍了2023年民航业发展目标：民航业将按照安全第一、市场主导、保障先行的原则，在做好运行保障能力评估的基础上，把握好行业恢复发展的节奏．下列航空图标，其文字上方的图案是轴对称图形的是（ ）
A．春秋航空B．东方航空
C．深圳航空D．海南航空
2．一个三角形三个内角的度数之比为5：4：9，这个三角形一定是（ ）
A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形
3．小芳有两根长度为和的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为（ ）的木条.
A．B．C．D．
4．平面直角坐标系中，与点关于x轴对称的点的坐标为（ ）
A．B．C．D．
5．如图，在Rt△ABC中，∠ABC＝90°，∠A＝65°，将其折叠，使点A落在边CB上A′处，折痕为BD，则∠A′DC＝（ ）
A．40°B．30°C．25°D．20°
6．如图，，现添加以下哪个条件不能判定的是（ ）
A．B．C．D．
7．如图，已知，，过点A，且，，垂足分别为点D，E，，，则的长为（ ）
A．10B．8C．4D．2
8．课本中给出了用直尺和圆规作的平分线的方法．
该作图依据是（ ）
A．B． C．D．
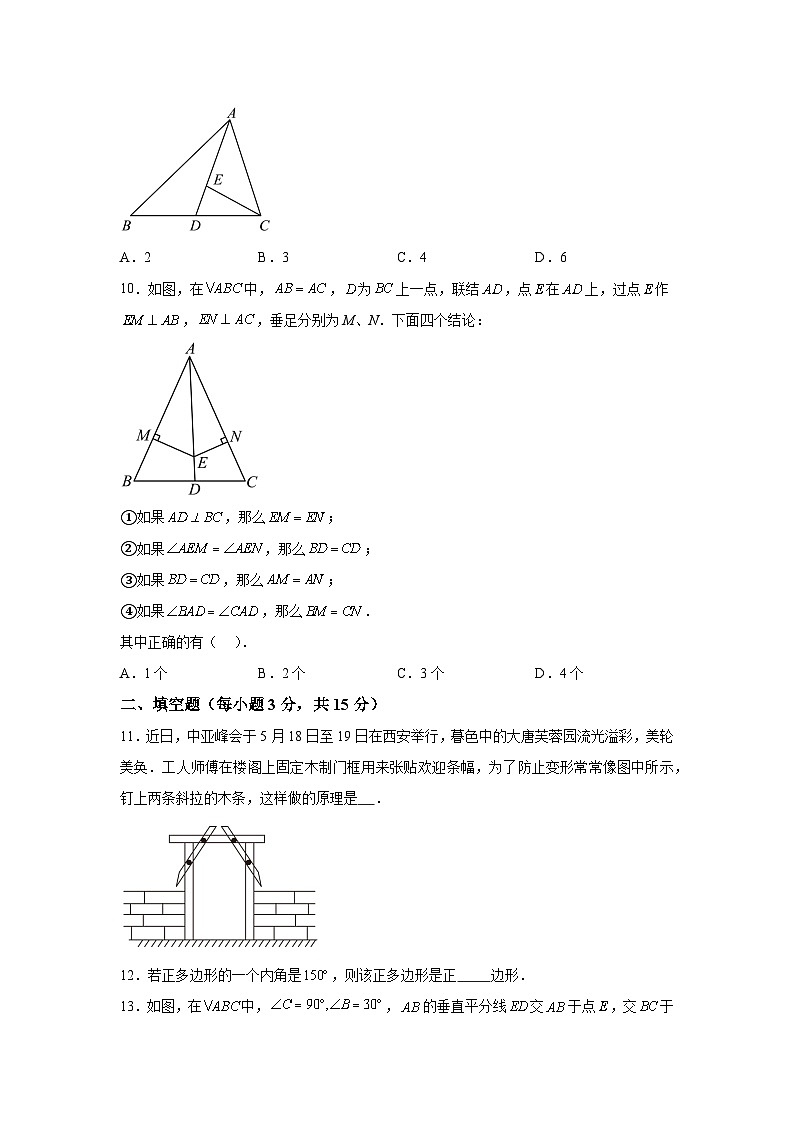
9．如图，AD是△ABC的中线，点E在线段AD上，且．若△DEC的面积是1，则△ABD的面积是（ ）
A．2B．3C．4D．6
10．如图，在中，，为上一点，联结，点在上，过点作，，垂足分别为M、N．下面四个结论：

①如果，那么；
②如果，那么；
③如果，那么；
④如果，那么．
其中正确的有（ ）．
A．1个B．2个C．3个D．4个
二、填空题（每小题3分，共15分）
11．近日，中亚峰会于5月18日至19日在西安举行，暮色中的大唐芙蓉园流光溢彩，美轮美奂．工人师傅在楼阁上固定木制门框用来张贴欢迎条幅，为了防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是 ．

12．若正多边形的一个内角是，则该正多边形是正 边形．
13．如图，在中，，的垂直平分线交于点，交于点．若，则的长为 ．

14．如图，在等腰中，，，作于点，，点为边上的中点，点为上一动点，则的最小值为 ．
15．如图，ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，直线l经过点C且与边AB相交．动点P从点A出发沿A→C→B路径向终点B运动；动点Q从点B出发沿B→C→A路径向终点A运动．点P和点Q的速度分别为2cm/s和3cm/s，两点同时出发并开始计时，当点P到达终点B时计时结束．在某时刻分别过点P和点Q作PE⊥l于点E，QF⊥l于点F，设运动时间为t秒，则当t＝ 秒时，PEC与QFC全等．
三、解答题（本大题共8个小题，共75分）
16．如图，是边上的高，平分交于点，若，，求和的度数．
17．如图，已知A（3，4），B（1，2），C（5，1）是平面直角坐标系中的三点．
（1）请画出△ABC关于y轴对称的△A1B1C1；
（2）分别写出点A1，B1，C1的坐标；
（3）连接AA1，BB1，求四边形AA1B1B的面积．
18．如图，线段与交于点，点为上一点，连接、、，已知，．

(1)请添加一个条件________使，并说明理由．
(2)在（1）的条件下请探究与的数量关系，并说明理由．
19．如图，在中，，，在线段BC上找一点D（与B，C不重合），使得和均为等腰三角形．
(1)一同学的解法是，如图1，以B为圆心，以的长为半径画弧与交于点D，请根据这种作法说明和均为等腰三角形；
(2)尺规作图：请在图2中用另外一种方法找出点D（保留作图痕迹，不写作法）．
20．如图，点A、B、C在同一直线上，△ABD，△BCE都是等边三角形．
（1）求证：AE=CD；
（2）若M，N分别是AE，CD的中点，试判断△BMN的形状，并证明你的结论．
21．如图，在中，垂直平分平分．

(1)若，求的度数；
(2)若，与的周长之差为，且的面积为，求的面积．
22．如图，是边长是的等边三角形，动点同时从A，B两点出发，分别沿方向 匀速运动，其中点P运动的速度是，点Q运动的速度是，当点Q到达点C时，两点都停止运动，设运动时间为t（s），解答下列问题：
(1)当点Q到达点C时，与的位置关系如何？请说明理由．
(2)在点P与点Q的运动过程中，是否能成为等边三角形？若能，请求出t，若不能，请说明理由．
(3)当t为何值时，是直角三角形？
23．在Rt△ABC中，，，点D是直线AB上的一点，连接CD，将线段CD绕点C逆时针旋转90°，得到线段CE，连接EB．
(1)操作发现
如图1，当点D在线段AB上时，请你直接写出AB与BE的位置关系为______；线段BD、AB、EB的数量关系为______；
(2)猜想论证
当点D在直线AB上运动时，如图2，是点D在射线AB上，如图3，是点D在射线BA上，请你写出这两种情况下，线段BD、AB、EB的数量关系，并对图2的结论进行证明；
(3)拓展延伸
若，，请你直接写出△ADE的面积．
答案与解析
1．D
【分析】本题考查了轴对称图形，熟记“轴对称图形沿一条直线对折后直线两旁的图像能完全重合”是解题关键．
【详解】解：A选项沿一条直线对折后直线两旁的图像不能完全重合，故不符合题意；
B选项沿一条直线对折后直线两旁的图像不能完全重合，故不符合题意；
C选项沿一条直线对折后直线两旁的图像不能完全重合，故不符合题意；
D选项沿一条直线对折后直线两旁的图像能完全重合，故符合题意．
故选：D．
2．B
【分析】本题考查了三角形的内角和，三角形的判定，能通过角度对三角形进行分类是解题关键．
【详解】解：设三角形内角分别为，
三角形内角和为，
，
解得：，
故三角形三个内角的度数分别为，，．
故三角形为直角三角形．
3．C
【分析】设木条的长度为xcm，再由三角形的三边关系即可得出结论．
【详解】设木条的长度为，则，即，
故她应该选择长度为的木条.
故选
【点睛】本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边之差小于第三边是解答此题的关键．
4．D
【分析】本题考查了平面直角坐标系，熟记“关于x轴对称的点横坐标不变，纵坐标变为原来的相反数”是解题关键．
【详解】解：由关于x轴对称的点横坐标不变，纵坐标变为原来的相反数，
得：点关于x轴对称的点的坐标为．
故选：D．
5．A
【分析】根据折叠的性质得到∠BA′D＝∠A＝65°，根据三角形的外角的性质计算即可．
【详解】解：由折叠的性质可知，∠BA′D＝∠A＝65°，
∵∠ABC＝90°，∠A＝65°，
∴∠C＝25°，
∴∠A′DC＝∠BA′D﹣∠C＝40°，
故选：A．
【点睛】本题主要考查折叠问题及三角形外角的性质，根据折叠得出∠BA′D＝∠A＝65°是解题的关键.
6．C
【分析】一般全等三角形的判定方法有SAS，ASA，AAS，SSS，根据定理逐个判断即可．
【详解】解：A、∠A=∠C，，BD=BD，符合AAS，即能推出，故本选项错误；
B、，，BD=BD，符合ASA，即能推出，故本选项错误；
C、,，BD=BD，不符合全等三角形的判定定理，即不能推出，故本选项正确；
D、AD=CD，，BD=BD，，符合SAS，即能推出，故本选项错误.
故选：C．
【点睛】本题考查了全等三角形的性质和判定，能正确根据全等三角形的判定定理进行推理是解此题的关键，注意：一般全等三角形的判定方法有SAS，ASA，AAS，SSS．
7．B
【分析】利用同角的余角相等证出，由证明，得出，即可得出结论．
【详解】证明：∵，，，
∴，
∴，，
∴，
在和中，
，
∴（），
∴，
∵，
∴，
故选：B．
【点睛】本题考查全等三角形的判定与性质，证明全等三角形得出对应边相等是解题的关键．
8．D
【分析】首先利用基本作图得到，，则根据可证得，再根据全等三角形的性质，即可证得结论
【详解】解：如图：连接，，
由作法得，，
又，
，
，
即射线就是的平分线．
故选：D．
【点睛】本题考查了作图−基本作图，全等三角形的判定与性质，熟练掌握5种基本作图是解决问题的关键．
9．B
【分析】根据可得，根据AD是△ABC的中线，可得，即可求解．
【详解】解：∵，
∴，
△DEC的面积是1，
，
AD是△ABC的中线，
．
故选B．
【点睛】本题考查了三角形中线的性质，掌握三角形中线的性质是解题的关键．
10．D
【分析】①，，根据等腰三角形的性质，可证得是的角平分线，又由，，根据角平分线的性质，即可证得；
②根据证明，利用全等三角形的性质和等腰三角形的性质得出；
③根据等腰三角形的性质和全等三角形的判定和性质得出；
④根据全等三角形的判定和性质以及等腰三角形的性质得出．
【详解】解：①∵，，
∴，
∵，，
∴，故①正确；
②∵，，
∴，
∵，
∴；故②正确；
③∵，，
∴，
∵，，
∴，
∴，
∴；故③正确；
④∵，，
∵，，
∴，
∴，
∴，
∴．故④正确；
故选：D．
【点睛】此题考查了角平分线的性质、等腰三角形的性质以及全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
11．三角形具有稳定性
【分析】根据三角形具有稳定性解答即可．
【详解】解：根据题意，为了防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是三角形具有稳定性，
故答案为：三角形具有稳定性．
【点睛】本题考查三角形的稳定性，能够运用数学知识解释生活中的现象是解答的关键．
12．十二
【分析】本题考查了正多边形的外角和，正多边形的判断，掌握正多边形的外角和为是解题关键．
【详解】解：设正多边形有n边，
由正多边形的一个内角是，得
正多边形的一个外角是，
正多边形的外角和为，
，
故答案为：十二．
13．
【分析】连接，根据线段垂直平分线的性质可得，，可得，从而可得，为的角平分线，由角平分线的性质得，再根据直角三角形角所对的直角边等于斜边的一半可得，即可求得结果．
【详解】解：连接，

∵的垂直平分线交于点，交于点，
∴，，
∴，
∵，
∴，
∴，
∴为的角平分线，
∵，，
∴，
∵，，
∴，
故答案为：．
【点睛】本题主要考查了垂直平分线的性质，角平分线的性质定理，含角的直角三角形．理解角平分线上的点到角的两边距离相等，直角三角形角所对的直角边等于斜边的一半是解题的关键．
14．4
【分析】先作出点A关于BC的对称点A'：延长AD至A'，使AD=A'D，连接A'E，交BC于P，此时PA+PE的值最小，就是A'E的长，证明CD=A'E=4即可．
【详解】解：∵AB=AC，BC=8，AD⊥BC，
∴BD=CD=4，
∵AD=AB
∴∠B=30°，
∴∠BAD=∠CAD=60°，
延长AD至A'，使AD=A'D，连接A'E，交BC于P，此时PA+PE的值最小，就是A'E的长，
∵AD=AB，AA′=2AD，
∴AA'=AB=AC，∠CAA'=60°，
∴△AA'C是等边三角形，
∵E是AC的中点，
∴A'E⊥AC，
∴A'E=CD=4，即PA+PE的最小值是4，
故答案为：4．
【点睛】本题考查了轴对称，最短路径问题和直角三角形的性质，根据轴对称的性质作出对称点是解题的关键，掌握线段垂直平分线的性质和等边三角形的性质与判定的灵活运用．
15．2或或6
【分析】分点Q在BC上和点Q在AC上，根据全等三角形的性质列式计算．
【详解】解：由题意得，AP＝2t，BQ＝3t，
∵AC＝6cm，BC＝8cm，
∴CP＝6﹣2t，CQ＝8﹣3t，
①如图1，当△PEC≌△CFQ时，
则PC＝CQ，
即6﹣2t＝8﹣3t，
解得：t＝2，
②如图2，当点Q与P重合时，△PEC≌△QFC全等，
则PC＝CQ，
∴6﹣2t＝3t﹣8．
解得：t＝，
③如图3，当点Q与A重合时，△PEC≌△CFQ，
则PC=CQ，
即2t-6=6，
解得：t=6，
综上所述：当t＝2秒或秒或6秒时，△PEC与△QFC全等，
故答案为：2或或6．
【点睛】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等是解题的关键．
16．，
【分析】根据三角形高的定理得出，根据三角形内角和定理得到，根据三角形角平分线的定义得出，根据三角形的内角和定理即可求解．
【详解】解：是边上的高，
，
，
，
，
平分，
；
，
，
．
【点睛】本题考查了三角形内角和定理，三角形高的定义，三角形角平分线的定义，熟练掌握三角形内角和定理是解题的关键．
17．（1）△A1B1C1即为所求；见解析；（2）点A1，B1，C1的坐标分别为：（﹣3，4）、（﹣1，2）、（﹣5，1）；（3）四边形AA1B1B的面积为8．
【分析】（1）根据轴对称图形的性质作图即可；
（2）根据（1）所作的图，写出坐标即可；
（3）根据梯形的面积公式求解即可．
【详解】如图，
（1）△A1B1C1即为所求；
（2）点A1，B1，C1的坐标分别为：（﹣3，4）、（﹣1，2）、（﹣5，1）；
（3）连接AA1，BB1，
∴四边形AA1B1B的面积为：（2+6）×2＝8．
【点睛】本题考查了方格作图的问题，掌握轴对称图形的性质、梯形面积公式是解题的关键．
18．(1)，理由见解析；
(2)，理由见解析．
【分析】（1）利用判定定理，添加即可判断；
（2）利用全等三角形的判定与性质，再结合等角对等边即可判断．
【详解】（1）解：添加条件：，理由如下：
∵，，，
∴；
（2）解：，理由如下：
∵，
∴，
∵，
∴，
∴，
∴．
【点睛】本题考查了全等三角形的判定与性质以及等角对等边，掌握全等三角形的判定定理是解题的关键．
19．(1)见解析
(2)见解析
【分析】本题考查了等腰三角形的判定及性质，尺规作图，
（1）根据三角形内角和定理及等腰三角形的判定即可得出结果；
（2）利用垂直平分线的性质作图即可；
熟记等腰三角形的两腰相等，两底角相等，作已知直线的中垂线是解题关键．
【详解】（1）解：连接，如图
，，
．
由作图得：，
，
，
，
，
和均为等腰三角形；
（2）如图2，点D即为所求．
20．（1）证明见解析；（2）△MBN是等边三角形．
【分析】(1)利用SAS证明△AOC≌△BOD，则有AE＝CD；
(2)由△ABE≌△DBC，可证△ABM≌△DBN，从而得BM＝BN，∠MBN＝60°.
【详解】(1)证明：∵△ABD、△BCE都是等边三角形，
∴AB＝BD，BC＝BE，∠ABD＝∠CBE＝60°，
∴∠ABD＋∠DBE＝∠DBE＋∠CBE即∠ABE＝∠DBC，
∴在△ABE和△DBC中，
△ABE≌△DBC(SAS)．
∴AE＝CD．
(2)解：△MBN是等边三角形，理由如下：
∵△ABE≌△DBC，
∴∠BAE＝∠BDC．
∵AE＝CD，M、N分别是AE、CD的中点，
∴AM＝DN；
又∵AB＝DB．
∴△ABM≌△DBN．
∴BM＝BN，∠ABM＝∠DBN．
∴∠DBM＋∠DBN＝∠DBM＋∠ABM＝∠ABD＝60°．
∴△MBN是等边三角形．
21．(1)
(2)
【分析】（1）由线段垂直平分线的性质结合三角形外角的性质易求出，再根据角平分线的定义即得出，最后根据三角形内角和定理求解即可；
（2）由线段垂直平分线的性质结合与的周长之差为，即可求出．过点D作于H．由的面积为，，可求出，结合角平分线的性质定理可得出，即可计算．
【详解】（1）解：∵垂直平分，
∴，
∴．
∵，
∴．
∵平分，
∴，
∴；
（2）解：∵垂直平分，
∴，，，
∵，，，
∴，
∴，
∴，即．
过点D作于H．

∵的面积为，且，，
∴，
∴．
∵平分，
∴．
∴．
【点睛】本题考查线段垂直平分线的性质，三角形外角的性质，三角形内角和定理，角平分线的定义及其性质．熟练掌握上述知识是解题关键．在解（2）时正确作出辅助线也是解题关键．
22．(1)当点Q到达点C时，，见解析
(2)能，
(3)或
【分析】本题考查了直角三角形的判定，等边三角形的性质和判定，几何动点问题，熟练掌握含的直角三角形的性质是解题关键．
（1）先求出的长，可得P是中点，由等边三角形的性质即可求解．
（2）由等边三角形的性质列方程即可求解．
（3）分情况讨论，由直角三角形的性质列方程即可求解．
【详解】（1）解：当点Q到达点C时，，理由如下：
，当点Q到达点C时，则，
，
点P为的中点，
；
（2）能，
∵为等边三角形，
．
时，为等边三角形，
，
解得；
（3）根据题意得，，
，
当时，
，
，
，
即，
解得；
当时，同理可得，解得．
综上所述：当或时，是直角三角形．
23．(1)AB⊥BE，AB=BD+BE；
(2)见解析；
(3)72或8．
【分析】（1）证明△ACD≌△BCE（SAS）利用全等三角形的性质可得结论；（2）分两种情形，在图2和图3中，利用全等三角形的性质证明即可；（3）分两种情形，在图2和图3中，利用全等三角形的性质以及三角形的面积解决问题即可．
【详解】（1）如图1中，
∵∠ACB=∠DCE=90°，∴∠ACD=∠BCE，∵CA=CB，CD=CE，∴△ACD≌△BCE（SAS），∴AD=BE，∠CBE=∠A，∵CA=CB，∠ACB=90°，∴∠A=∠CBA=45°，∴∠CBE=∠A=45°，∴∠ABE=90°，∴AB⊥BE，∵AB=AD+BD，AD=BE，∴AB=BD+BE，故答案为AB⊥BE，AB=BD+BE．
（2）①如图2中，结论：BE=AB+BD．
理由：连接AE，DE，
∵∠ACB=∠DCE=90°，∴∠ACD=∠BCE，∵CA=CB，CD=CE，∴△ACD≌△BCE（SAS），∴AD=BE，∵AD=AB+BD，AD=BE，∴BE=AB+BD．②如图3中，结论：BD=AB+BE．
理由：连接AE，DE，
∵∠ACB=∠DCE=90°，∴∠ACD=∠BCE，∵CA=CB，CD=CE，∴△ACD≌△BCE（SAS）∴AD=BE，∵BD=AB+AD，AD=BE，∴BD=AB+BE．
（3）如图2中，∵AB=4，BD=8，∴BE=AD=BD+AB=8+4=12，∵BE⊥AD，∴S△ADE=•AD•EB=×12×12=72．如图3中，∵AB=4，BD=8，∴BE=AD=BD-AB=8-4=4，∵BE⊥AD，∴S△ADE=•AD•EB=×4×4=8．
【点睛】本题属于几何变换—旋转综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题．
作法
图形
1.以点O为圆心，任意长为半径作弧，分别交射线、于点C、D．
2.分别以点C、D为圆心，大于的长为半径作弧，两弧在的内部交于点M．
3.作射线．
就是的平分线．