浙江省杭州市2023年八年级上学期期末学业水平测试数学试题附答案

这是一份浙江省杭州市2023年八年级上学期期末学业水平测试数学试题附答案，共10页。试卷主要包含了单选题，解答题等内容，欢迎下载使用。
1．下列说法正确的是（ ）
A．每个定理都有逆定理B．每个命题都有逆命题
C．假命题没有逆命题D．真命题的逆命题是真命题
2．已知一次函数，若随的增大而减小，则它的图象经过（ ）
A．第一、二、三象限B．第一、二、四象限
C．第二、三、四象限D．第一、三、四象限
3．若，则下列式子中正确的是（ ）
A．B．
C．D．
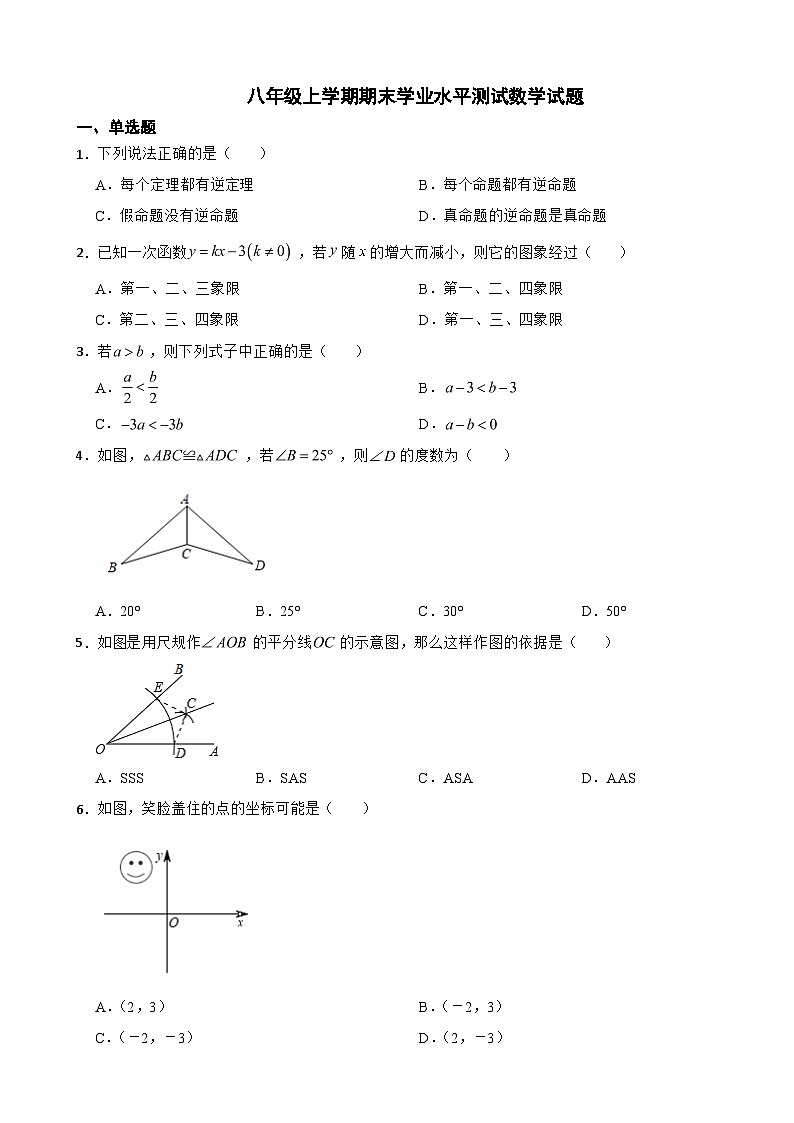
4．如图，，若，则的度数为（ ）
A．20°B．25°C．30°D．50°
5．如图是用尺规作的平分线的示意图，那么这样作图的依据是（ ）
A．SSSB．SASC．ASAD．AAS
6．如图，笑脸盖住的点的坐标可能是（ ）
A．（2，3）B．（－2，3）
C．（－2，－3）D．（2，－3）
7．小聪用100元钱去购买笔记本和钢笔共30件.已知每本笔记本2元，每支钢笔5元，小聪最多可以购买钢笔多少支？设小聪最多能买x支钢笔.可列出不等式（ ）
A．B．
C．D．
8．如图，在△ABC中，AB＝AC，AD平分∠BAC，DE⊥AB于E点，DF⊥AC于点F，则下列四个结论：①AD上任意一点到AB，AC两边的距离相等； ②AD⊥BC且BD＝CD；③∠BDE＝∠CDF；④AE＝AF.其中正确的有（ ）
A．②③B．①③C．①②④D．①②③④
9．如图，木杆斜靠在墙壁上，是的中点，当木杆的上端沿墙壁竖直下滑时，木杆的底端也随之沿着射线方向滑动，则下滑过程中的长度变化情况是（ ）
A．逐渐变大B．不断变小
C．不变D．先变大再变小
10．如图， 在中，，，与相交于点，于.则下列数量关系正确的为（ ）
A．B．
C．D．
二、填空题
11．定理“直角三角形的两个锐角互余”的逆定理是 ．
12．已知函数是一次函数，则的值为 .
13．不等式组的整数解有 个.
14．如图是一个滑梯示意图，左边是楼梯，右边是滑道，已知滑道与的长度相等，滑梯的高度，.则滑道的长度为 m.
15．如图， 一次函数与的图像相交于点，则方程组的解为 ，关于x的不等式的解为 .
16．如图，等边中，，O为垂足且，E是线段上的一个动点，连接，线段与线段关于直线对称，连接，在点E运动的过程中，当的长取得最小值时，的长为 .
三、解答题
17．已知：如图，点在同一条直线上，.求证：.
18．解下列不等式（组）
（1）；
（2）
19．如图
（1）在平面直角坐标系中，画，使其三个顶点为，，；
（2）是直角三角形吗？请证明你的判断.
20．已知y关于x的一次函数，当时，；当时，.
（1）求k、b的值；
（2）若，是该一次函数图象上的两点，求证：.
21．如图，已知都是等腰直角三角形，连接.
（1）求证：；
（2）若延长交于点F，试判断与的位置关系，并说明理由.
22．甲、乙两地相距3000千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段表示货车离甲地距离千米与时间小时之间的函数关系；线段表示轿车离甲地距离千米与时间小时之间的函数关系.点在线段上，请根据图象解答下列问题：
（1）试求点的坐标；
（2）当轿车与货车相遇时，求此时的值；
（3）在整个过程中，问在什么范围时，轿车与货车之间的距离小于30千米.
23．如图，点A在直线l上，在直线l右侧做等腰三角形，，，点D与点B关于直线l轴对称，连接交直线l于点E，连接.
（1）求证：；
（2）求证：；
（3）当时，求证：.
1．B
2．C
3．C
4．B
5．A
6．B
7．B
8．D
9．C
10．B
11．有两个角互余的三角形是直角三角形
12．2
13．5
14．10
15．；x＞1
16．
17．证明：∵，
∴，即，
在与中，
，
∴，
∴.
18．（1）解：
（2）解：令
解①得
解②得
∴ 不等式组的解是：
19．（1）解：如图所示：
（2）解：是直角三角形.
理由如下：
由勾股定理可知，，，
∵，
∴，
∴是直角三角形.
20．（1）解：把，；，代入，得
，解得
（2）证明：由（1）可知：函数解析式为，
把，代入解析式得：
，，
∴
21．（1）证明：∵都是等腰直角三角形，
∴，
∴，即，
在和中，
∵，
∴
（2）解：， 理由如下：
如图，设与交于点G，
∵，
∴，
∵
∴，
∴.
22．（1）解：设的函数解析式为.
，在其图象上，得
，
解得： ，，
，
令，解得
故
（2）解：的函数解析式：，；
∵，设的解析式为，
则，解得：
的函数解析式：，
，
解得，
当时，轿车与货车相遇；
（3）解：当时，，轿车还未行驶，两车相距30千米，故时，轿车与货车之间的距离小于30千米.
当时，，两车相距千米，故时，轿车与货车之间的距离小于30千米
当两车都在行驶时，由题意可得：
，
解得：.
故，，时两车相距小于30千米，
答：在整个过程中当轿车与货车相距小于30千米时，的取值范围为或或.
23．（1）证明：∵点D与点B关于直线l轴对称
∴，
∵，
∴，
∴
（2）证明：如图，设与交于点
∵点D与点B关于直线l轴对称
∴，，，
∴，
∴，
∵；
∴，
∵ （对顶角相等）；
∴；
（3）证明：当时，在中，由勾股定理可知：.
∵
∴.
∴.
在中，由勾股定理可知：.
又∵，
故，
∴.