浙江省湖州市2023年八年级上学期期末检测数学试题附答案

这是一份浙江省湖州市2023年八年级上学期期末检测数学试题附答案，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列图形中，不是轴对称图形的是（ ）
A．B．
C．D．
2．在平面直角坐标系中，点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
3．三角形的两边长分别为和，此三角形第三边长可能是（ ）
A．B．C．D．
4．如图所示，在数轴上表示不等式正确的是（ ）
A．B．C．D．
5．对于命题“如果，那么”，下面四组关于a，b的值中，能说明这个命题是假命题的是（ ）
A．，B．，
C．，D．，
6．已知点和点在直线上，且，则a的值可能是（ ）
A．-3B．-2C．1D．3
7．如图，在中，，点D是边的中点，若，则的度数为（ ）
A．B．C．D．
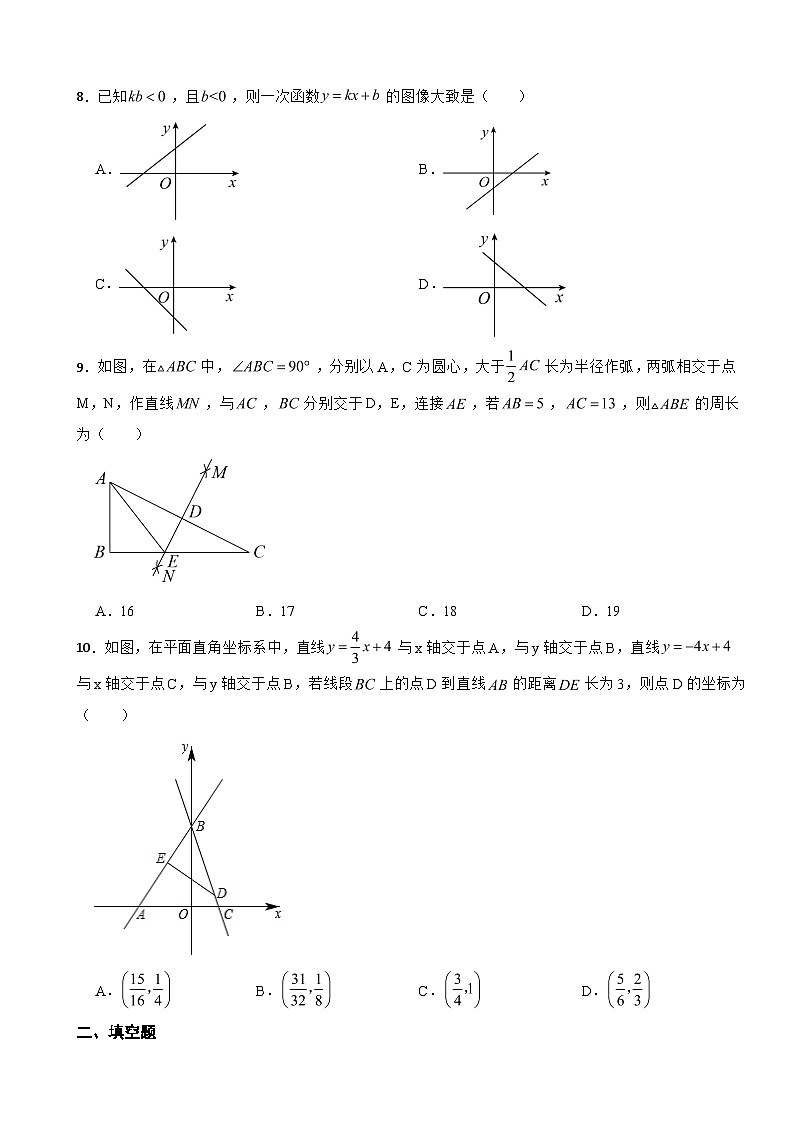
8．已知，且，则一次函数的图像大致是（ ）
A．B．
C．D．
9．如图，在中，，分别以A，C为圆心，大于长为半径作弧，两弧相交于点M，N，作直线，与，分别交于D，E，连接，若，，则的周长为（ ）
A．16B．17C．18D．19
10．如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B，直线与x轴交于点C，与y轴交于点B，若线段上的点D到直线的距离长为3，则点D的坐标为（ ）
A．B．C．D．
二、填空题
11．若点与点关于y轴对称，则a的值为 .
12．如果a＜b，那么﹣3a ﹣3b（用“＞”或“＜”填空）．
13．如图，已知，要使，还需添加一个条件，这个条件可以是 .（写出一个即可）
14．已知，如图直线与直线交于点，则不等式的解集为 .
15．如图，是直角三角形，，分别以、为边向两侧作正方形.若图中两个正方形的面积和，则 .
16．如图，在中，，，分别以，为边向外作正和正，连接，，当的边变化过程中，取最长时，则的长为 .
三、解答题
17．解下列不等式（组）：
（1）；
（2）.
18．已知y是x的一次函数，且当时，；当时，.
（1）求这个一次函数的表达式；
（2）当时，求出对应y的值.
19．如图，，，，点E在线段上.
（1）求证：；
（2）求的度数.
20．如图，在平面直角坐标系中，的三个顶点的坐标分别为，，.
（1）在图中作出关于原点的对称图形；
（2）请直接写出，，的坐标： ； ； .
21．如图，在中，，平分交于点D，作于点E.
（1）若，求的度数；
（2）若，，求的面积.
22．为提升学生的文学素养，培养学生的阅读兴趣，某校准备购进A，B两种图书.经调查，购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示，B种图书每本20元.
（1）当和时，求y与x之间的函数关系式；
（2）现学校准备购进300本图书，其中购进A种图书x本，设购进两种图书的总费用为w元.
①当时，求出w与x间的函数表达式；
②若购进A种图书不少于60本，且不超过B种图书本数的2倍，那么应该怎样分配购买A，B两种图书才能使总费用最少？最少总费用多少元？
23．【问题背景】
（1）如图1，点P是线段，的中点，求证：；
（2）【变式迁移】
如图2，在等腰中，是底边上的高线，点E为内一点，连接，延长到点F，使，连接，若，若，，求的长；
（3）【拓展创新】
如图3，在等腰中，，，点D为中点，点E在线段上（点E不与点B，点D重合），连接，过点A作，连接，若，，请直接写出的长.
24．如图1，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B，并与直线相交于点C.
（1）求点C的坐标；
（2）如图2，点D在点C右侧的x轴上，过点D作x轴的垂线与直线交于点E，与直线交于点F，且.
①求点E的坐标；
②若点M是射线上的动点，连接，并在左侧作等腰直角，当顶点P恰好落在直线上时，求出对应的点M的坐标.
1．C
2．B
3．C
4．A
5．D
6．D
7．B
8．B
9．B
10．A
11．5
12．＞
13．AC=AD（答案不唯一）
14．x＜1
15．6
16．
17．（1）解：，
移项得：，
合并同类项得：，
未知数系数化为1得：
（2）解：，
解不等式①得：，
解不等式②得：，
∴不等式组的解集为：
18．（1）解：设一次函数解析式为，把，；，代入得：
，
解得：，
∴一次函数的表达式为
（2）解：把代入得：
.
19．（1）证明：∵，
∴，即.
∴在和中，
∴.
（2）解：∵，
∴，
∵，
∴
20．（1）解：如图：即为所求：
（2）（0，-3）；（4，-4）；（2，-1）
21．（1）解：平分，
，
，
，
，
，
，
；
（2）解：平分，，，
，
，
，
，，
，，，
，
设，
，
，
，
解得，
，
的面积为：
.
22．（1）解：当时，设，
将代入解析式，得，
解得，
，
当时，设，
将、分别代入解析式，
得
解得，
，
综上，
（2）解：①当时，
；
②，，
，
此时，
，
随x的增大而减小，
当时，w最小，最小值为：，
故购买A种200本，B种100本时总费用最少，最少总费用为5800元.
23．（1）证明：点P是线段，的中点，
，，
在和中，
，
，
；
（2）解：如图：连接，
在等腰中，是底边上的高线，
，
在和中，
，
，，
，
，
，
，，
，
；
（3）解：
24．（1）解：联立，
解得：，
∴点C的坐标为
（2）解：①设点E的坐标为，则点F的坐标为，
∵，
∴，
解得：，
∴点E的坐标为；
②当时，
把代入得：，
∴，
∵，
∴，
∴为等腰直角三角形，
∴点P与点O重合，点B与点M重合，
∴点M坐标为；
当时，过点M作于点G，过点P作于点H，如图所示：
设点M的坐标为，则，
∵点D的横坐标为4，
∴，
∵，，
∴，
∵，
∴，，
∴，
∵，
∴，
∴，
，
∴点P的横坐标为：，纵坐标为：，
即，
把代入得：
，
解得：，
∵，
∴不符合题意舍去；
当时，过点M作直线轴，交直线于点K，过点P作直线轴，交直线l于点Q，如图所示：
则四边形是矩形，
同理可证，
∴，，
∵，，
∴，，
∴，
∴点P的纵坐标为，横坐标为，
即，
把点代入得：
，
解得：，
符合题意，
∴，
∴点M的坐标为：；
综上所述，点M的坐标为或.