高考数学一轮复习第3章第5课时利用导数解决恒(能)成立问题学案

这是一份高考数学一轮复习第3章第5课时利用导数解决恒(能)成立问题学案，共22页。
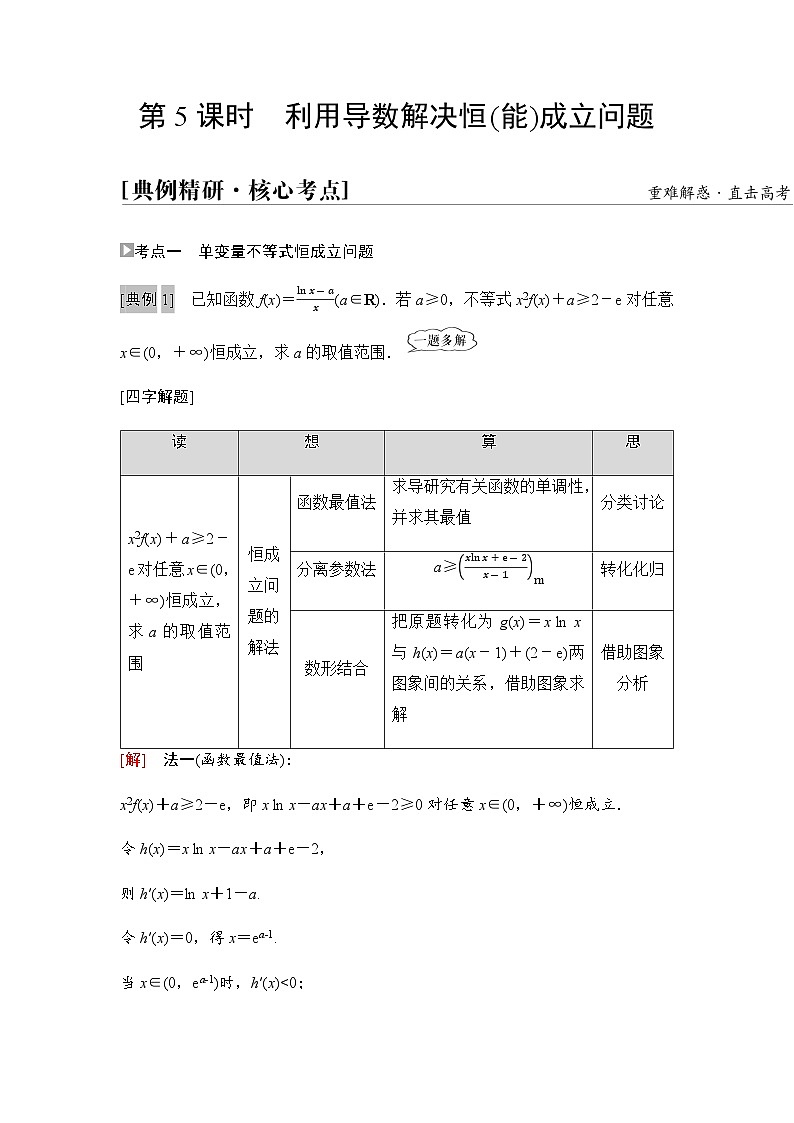
[典例1] 已知函数f(x)＝lnx-ax(a∈R)．若a≥0，不等式x2f(x)＋a≥2－e对任意x∈(0，＋∞)恒成立，求a的取值范围．
[四字解题]
[解] 法一(函数最值法)：
x2f(x)＋a≥2－e，即x ln x－ax＋a＋e－2≥0对任意x∈(0，＋∞)恒成立．
令h(x)＝x ln x－ax＋a＋e－2，
则h′(x)＝ln x＋1－a.
令h′(x)＝0，得x＝ea-1.
当x∈(0，ea-1)时，h′(x)0.
所以h(x)的最小值是h(ea-1)＝a＋e－2－ea-1.
令t(a)＝a＋e－2－ea-1，则t′(a)＝1－ea-1.
令t′(a)＝0得a＝1.
当a∈[0，1)时，t′(a)>0，t(a)在[0，1)上单调递增；
当a∈(1，＋∞)时，t′(a)0；
当a∈(1，＋∞)时，h(x)的最小值为t(a)≥t(2)＝0.
故a∈[0，2].
法二(分离参数法)：
原式可变为x ln x＋e－2≥a(x－1)(*)对任意x∈(0，＋∞)恒成立．
当x∈(0，1)时，分离变量可得a≥xlnx+e-2x-1.
令g(x)＝x ln x，
先求出函数g(x)＝x ln x的最小值．
求得g′(x)＝ln x＋1.
当x∈(0，e-1)时，g′(x)0，g(x)单调递增．
所以g(x)min＝g(e-1)＝－e-1.
因为此时(x ln x)min＝－e-1，
所以x ln x＋e－2≥－e-1＋e－2>0.
又因为x∈(0，1)，所以xlnx+e-2x-10，
所以h(x)单调递增．
即x＝e是t′(x)＝x-lnx-e-1x-12的唯一零点．
当x∈(1，e)时，t′(x)0，t(x)单调递增．
所以a≤t(x)min＝t(e)＝2，故a∈[0，2].
法三(数形结合)：
通过变形原不等式等价于证明：x ln x≥a(x－1)＋(2－e)，x∈(0，＋∞)．
若令g(x)＝x ln x和h(x)＝a(x－1)＋(2－e)．
则只需证明函数g(x)的图象在直线h(x)的上方．
首先分析g(x)＝x ln x的图象．
由法二可知：当x∈(0，e-1)时，g(x)单调递减；
当x∈(e-1，＋∞)时，g(x)单调递增，
且g(x)min＝g(e-1)＝－e-1.
其次分析h(x)＝a(x－1)＋(2－e)的图象．
因为a≥0，所以h(x)表示过定点(1，2－e)的非减函数，
且g(x)min＝－e-1>2－e.
两个函数的图象大致如图1所示：

图1 图2
所以如果能说明当g(x)和h(x)相切时二者只有一个切点，如图2，就能求出a的最大值．
设g(x)和h(x)相切于点P(x0，y0)，则可得ax0-1+2-e=x0lnx0①，a=g'x0=lnx0+1②.
消去ln x0得2－e＝a－ea-1③.
易得a＝2为③式的解．
令t(a)＝a－ea-1＋e－2，t′(a)＝1－ea-1.
当t′(a)＝0时，a＝1.
当a∈[0，1)时，t′(a)＞0，t(a)单调递增；
当a∈(1，＋∞)时，t′(a)0且t(1)＝e－2>0，
所以函数t(a)在区间[0，1]上无零点，
又t(2)＝0，所以函数t(a)在区间(1，＋∞)上有且仅有一个零点，a＝2.
综上所述，a∈[0，2].
【教师备选题】
(2022·重庆三模)已知函数fx＝a cs x＋x sin x＋b在点π2，fπ2处的切线方程为y＝π2＋1.
(1)求函数fx在-π，π上的单调区间；
(2)当x∈0，5π4时，是否存在实数m使得fx≤mx-π恒成立，若存在，求实数m的取值集合，若不存在，说明理由．
(附：2π2+4≈19.6，5π＋4≈19.7)
[解] (1)由题意知fπ2＝π2＋1，即π2＋b＝π2＋1，得b＝1，
因为f′x＝－a sin x＋sin x＋x cs x，
所以f′π2＝－a＋1＝0，得a＝1，所以f′x＝x cs x，
当0