河南省漯河市郾城区2023-2024学年九年级上学期期中数学试卷

这是一份河南省漯河市郾城区2023-2024学年九年级上学期期中数学试卷，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下面图形中，不是中心对称图形的是（ ）
A．B．
C．D．
2．（3分）把方程x2+x＝3（x﹣2）化成ax2+bx+c＝0的形式，则a，b，c的值分别为（ ）
A．1，﹣2，2B．1，﹣3，6C．1，﹣2，6D．1，4，6
3．（3分）关于二次函数y＝﹣（x﹣2）2的图象，下列说法正确的是（ ）
A．开口向上
B．最高点是（2，0）
C．对称轴是直线x＝﹣2
D．当x＞0时，y随x的增大而减小
4．（3分）用配方法解方程x2+2x﹣5＝0时，下列配方结果正确的是（ ）
A．（x﹣1）2＝5B．（x+1）2＝6C．（x+1）2＝7D．（x﹣1）2＝6
5．（3分）下面语句中，不正确的是（ ）
A．相等的圆心角所对的弦相等
B．不在同一条直线上的三个点确定一个圆
C．圆内接平行四边形是矩形
D．圆的直径所对应的两条弧是等弧
6．（3分）要组织一次篮球联赛，赛制为单循环形式（每两队之间都只赛一场），计划安排15场比赛．如果设邀请x个球队参加比赛，那么根据题意可以列方程为（ ）
A．2x＝15B．x（x+1）＝15
C．x（x﹣1）＝15D．
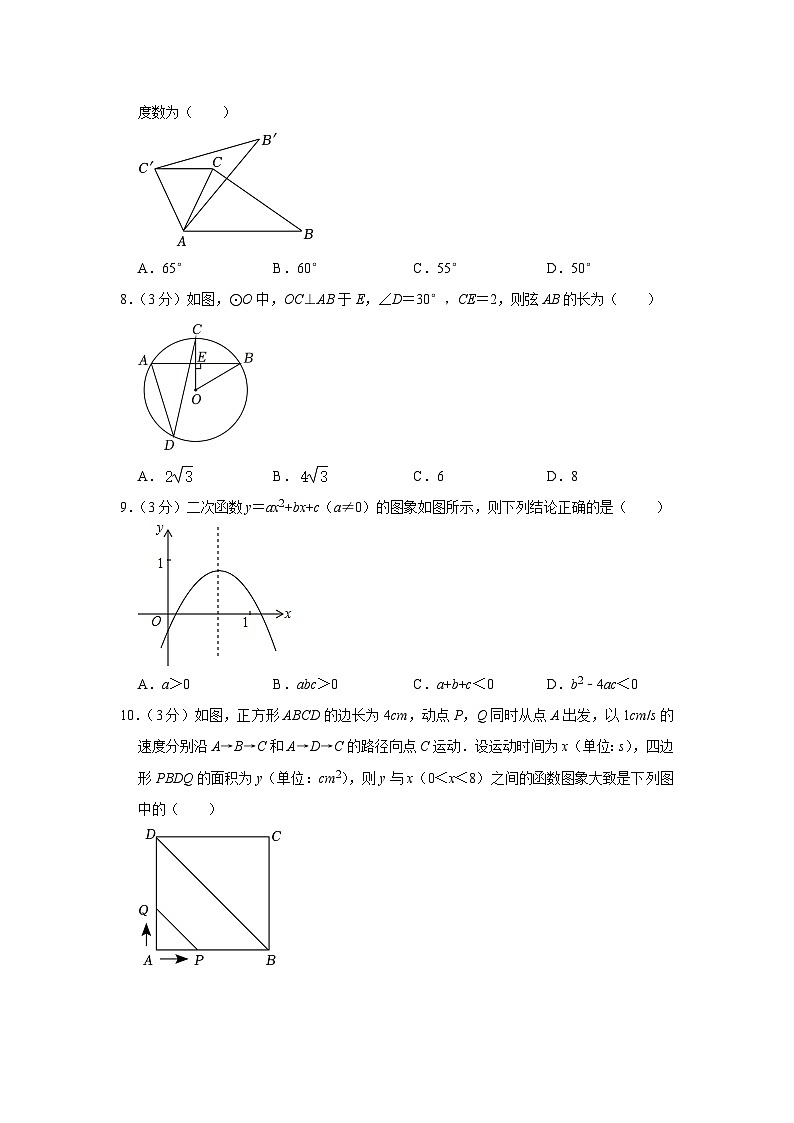
7．（3分）如图，将△ABC在平面内绕点A旋转到△AB'C'的位置，∠BAB'＝50°，则∠ACC'度数为（ ）
A．65°B．60°C．55°D．50°
8．（3分）如图，⊙O中，OC⊥AB于E，∠D＝30°，CE＝2，则弦AB的长为（ ）
A．B．C．6D．8
9．（3分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的是（ ）
A．a＞0B．abc＞0C．a+b+c＜0D．b2﹣4ac＜0
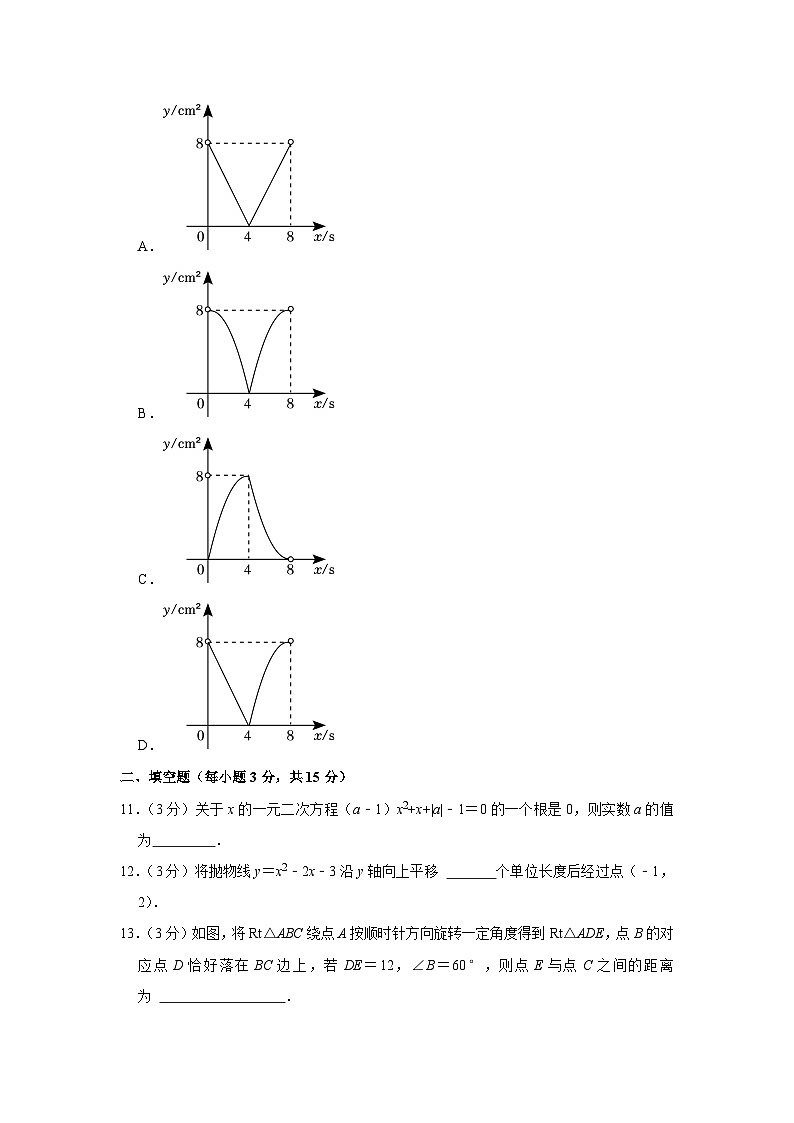
10．（3分）如图，正方形ABCD的边长为4cm，动点P，Q同时从点A出发，以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动．设运动时间为x（单位：s），四边形PBDQ的面积为y（单位：cm2），则y与x（0＜x＜8）之间的函数图象大致是下列图中的（ ）
A．
B．
C．
D．
二、填空题（每小题3分，共15分）
11．（3分）关于x的一元二次方程（a﹣1）x2+x+|a|﹣1＝0的一个根是0，则实数a的值为 ．
12．（3分）将抛物线y＝x2﹣2x﹣3沿y轴向上平移 个单位长度后经过点（﹣1，2）．
13．（3分）如图，将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若DE＝12，∠B＝60°，则点E与点C之间的距离为 ．
14．（3分）如图，PA，PB分别与⊙O相切于点A，B，AC为⊙O的直径，若∠C＝60°，则△PAB的形状是 ．
15．（3分）如图，在▱ABFE中，AB＝4，AE＝2，点E在⊙A上，O是▱ABFE的对称中心，O'是正方形ABCD的对称中心，若OO'＝d，则d的取值范围 ．
三、解答题（本大题共8个小题，共75分）
16．（10分）解方程：
（1）x2+2x﹣1＝0；
（2）（2x﹣1）2＝4x﹣2．
17．（9分）在平面直角坐标系中，△ABC的三个顶点都在边长均为1个单位长度的正方形网格的格点上．
（1）画出△ABC关于原点对称的图形△A1B1C1，并写出点C1的坐标；
（2）画出△ABC绕点O逆时针旋转90°后的图形△A2B2C2，并写出点B2的坐标；
（3）写出△A1B1C1经过怎样的旋转可直接得到△A2B2C2．
18．（9分）已知关于x的一元二次方程x2+（2m+1）x+m﹣2＝0．
（1）求证：无论m取何值，此方程总有两个不相等的实数根；
（2）当该方程的判别式的值最小时，写出m的值，并求出此时方程的解．
19．（9分）已知，如图，在△ABC中，∠ACB＝90°，请根据下列要求解决问题：
（1）利用尺规作出△ABC的内切圆⊙O；（不写作法，保留作图痕迹）
（2）若S△ABC＝6，内切圆⊙O的半径为1，求△ABC的周长．
20．（9分）某商品的进价为每件30元，现在的售价为每件40元，每星期可卖出150件．市场调查反映：如果每件的售价每涨1元（售价每件不能高于45元），那么每星期少卖10件．设每件涨价x元（x为非负整数），每星期的销量为y件．
（1）求y与x的函数关系式及自变量x的取值范围；
（2）如何定价才能使每星期的利润最大且每星期的销量较大？每星期的最大利润是多少？
21．（9分）已知，如图，在△ADC中，∠ADC＝90°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，∠BED＝2∠C．
（1）求证：BF是⊙O的切线；
（2）若BF＝FC，，求⊙O的半径．
22．（10分）在平面直角坐标系中，已知二次函数y＝﹣x2+bx+c的图象经过点（1，0）和（﹣3，0）．
（1）求二次函数的解析式，并写出此图象的顶点坐标；
（2）若点A（﹣2，y1），B（x2，y2）都在其图象上，且y1＞y2，则x2的取值范围是 ；
（3）已知点P（m，m）与点Q均在该函数图象上（其中m＞0），且这两点关于该函数图象的对称轴对称，求m的值及点Q到x轴的距离．
23．（10分）如图①，在△ABC中，∠A＝90°，AB＝AC＝3，点D，E分别在边AB，AC上，，连接DE．将△ADE绕点A顺时针方向旋转，旋转角为α（0°＜α＜360°）．
（1）如图②，当α＝90°时，连接CE，BD，填空：CE与BD的数量关系为： ；CE与BD的位置关系为： ；
（2）当0°＜α＜180°时，CE与BD交于点F，（1）中的结论还成立吗？若成立，请结合图③写出证明过程；若不成立，请说明理由；
（3）当△ADE旋转到ED⊥AC时，请直接写出BD的长．
2023-2024学年河南省漯河市郾城区九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（每小题3分，共30分）
1．（3分）下面图形中，不是中心对称图形的是（ ）
A．B．
C．D．
【解答】解：选项A、C、D中的图形都能找到一个点，使图形绕某一点旋转180°后与原来的图形重合，所以是中心对称图形．
选项B中的图形不能找到一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形．
故选：B．
2．（3分）把方程x2+x＝3（x﹣2）化成ax2+bx+c＝0的形式，则a，b，c的值分别为（ ）
A．1，﹣2，2B．1，﹣3，6C．1，﹣2，6D．1，4，6
【解答】解：x2+x＝3（x﹣2），
x2+x＝3x﹣6，
x2+x﹣3x+6＝0，
x2﹣2x+6＝0，
这里a＝1，b＝﹣2，c＝6，
故选：C．
3．（3分）关于二次函数y＝﹣（x﹣2）2的图象，下列说法正确的是（ ）
A．开口向上
B．最高点是（2，0）
C．对称轴是直线x＝﹣2
D．当x＞0时，y随x的增大而减小
【解答】解：∵二次函数y＝﹣（x﹣2）2的图象开口向下，
∴对称轴是直线x＝2，顶点坐标是（2，0），
∴函数有最高点（2，0），当x＞2时，y随x的增大而减小．
说法正确的是B，
故选：B．
4．（3分）用配方法解方程x2+2x﹣5＝0时，下列配方结果正确的是（ ）
A．（x﹣1）2＝5B．（x+1）2＝6C．（x+1）2＝7D．（x﹣1）2＝6
【解答】解：移项，得
x2+2x＝5，
配方，得
x2+2x+1＝5+1，
即（x+1）2＝6，
故选：B．
5．（3分）下面语句中，不正确的是（ ）
A．相等的圆心角所对的弦相等
B．不在同一条直线上的三个点确定一个圆
C．圆内接平行四边形是矩形
D．圆的直径所对应的两条弧是等弧
【解答】解：A、在同圆或等圆中，相等的圆心角所对的弦相等，原说法错误，符合题意；
B、不在同一条直线上的三个点确定一个圆，正确，不符合题意；
C、圆内接平行四边形是矩形，正确，不符合题意；
D、圆的直径所对应的两条弧是等弧，正确，不符合题意．
故选：A．
6．（3分）要组织一次篮球联赛，赛制为单循环形式（每两队之间都只赛一场），计划安排15场比赛．如果设邀请x个球队参加比赛，那么根据题意可以列方程为（ ）
A．2x＝15B．x（x+1）＝15
C．x（x﹣1）＝15D．
【解答】解：设邀请x个队，每个队都要赛（x﹣1）场，但两队之间只有一场比赛，
由题意得，＝15，
故选：D．
7．（3分）如图，将△ABC在平面内绕点A旋转到△AB'C'的位置，∠BAB'＝50°，则∠ACC'度数为（ ）
A．65°B．60°C．55°D．50°
【解答】解：∵将△ABC在平面内绕点A旋转到△AB'C'的位置，
∴∠C'AC＝∠BAB'＝50°，AC＝AC'，
∴∠ACC'＝∠AC'C＝＝65°，
故选：A．
8．（3分）如图，⊙O中，OC⊥AB于E，∠D＝30°，CE＝2，则弦AB的长为（ ）
A．B．C．6D．8
【解答】解：∵OC⊥AB于E，
∴＝，AE＝BE＝AB，
∴∠BOC＝2∠D＝60°，
∴∠BOE＝30°，
∴OB＝2OE，
∵OE＝OC﹣CE＝OB﹣CE，CE＝2，
∴OE＝OB﹣2，
∴OB＝OB﹣2，
∴OB＝4，
∴OE＝2，
∴BE＝＝2，
∴AB＝4，
故选：B．
9．（3分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的是（ ）
A．a＞0B．abc＞0C．a+b+c＜0D．b2﹣4ac＜0
【解答】解：由抛物线的开口向下可得a＜0，
由抛物线的对称轴在y轴的右侧可得x＝﹣＞0，则b＞0，
由抛物线与y的交点在y轴的负半轴可得c＜0，
则有abc＞0，
结合图象可得，当x＝1时y＝a+b+c＞0，
由抛物线与x轴有两个交点可得b2﹣4ac＞0．
故选：B．
10．（3分）如图，正方形ABCD的边长为4cm，动点P，Q同时从点A出发，以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动．设运动时间为x（单位：s），四边形PBDQ的面积为y（单位：cm2），则y与x（0＜x＜8）之间的函数图象大致是下列图中的（ ）
A．
B．
C．
D．
【解答】解：①0＜x≤4时，
∵正方形的边长为4cm，
∴y＝S△ABD﹣S△APQ，
＝×4×4﹣•x•x，
＝﹣x2+8，
②4≤x＜8时，
y＝S△BCD﹣S△CPQ，
＝×4×4﹣•（8﹣x）•（8﹣x），
＝﹣（8﹣x）2+8，
所以，y与x之间的函数关系可以用两段二次函数图象表示，纵观各选项，只有B选项图象符合．
故选：B．
二、填空题（每小题3分，共15分）
11．（3分）关于x的一元二次方程（a﹣1）x2+x+|a|﹣1＝0的一个根是0，则实数a的值为 ﹣1 ．
【解答】解：∵关于x的一元二次方程（a﹣1）x2+x+|a|﹣1＝0的一个根是0，
∴|a|﹣1＝0，
即a＝±1，
∵a﹣1≠0
∴a＝﹣1，
故答案为：﹣1．
12．（3分）将抛物线y＝x2﹣2x﹣3沿y轴向上平移 2 个单位长度后经过点（﹣1，2）．
【解答】解：设将抛物线y＝x2﹣2x﹣3沿y轴向上平移k个单位长度后经过点（﹣1，2）．
平移后的表达式为：y＝（x﹣1）2﹣4+k，
∵经过点（﹣1，2），代入得：2＝（﹣1﹣1）2﹣4+k，
∴k＝2．
故答案为：2．
13．（3分）如图，将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若DE＝12，∠B＝60°，则点E与点C之间的距离为 6 ．
【解答】解：如图，连接EC，
∵将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE，
∴DE＝BC＝12，AD＝AB，AC＝AE，∠DAB＝∠EAC，
∵∠B＝60°，
∴∠ACB＝30°，
∴AB＝BC＝6，AC＝AB＝6，
∵AD＝AB，∠B＝60°，
∴△ABD是等边三角形，
∴∠DAB＝60°＝∠EAC，
∴△ACE是等边三角形，
∴AC＝AE＝EC＝6，
故答案为：6．
14．（3分）如图，PA，PB分别与⊙O相切于点A，B，AC为⊙O的直径，若∠C＝60°，则△PAB的形状是 等边三角形 ．
【解答】解：如图，连接OB，
∵AC为⊙O的直径，
∴∠ABC＝90°，
由圆周角定理得：∠AOB＝2∠C＝120°，
∵PA，PB分别与⊙O相切于点A，B，
∴OA⊥PA，OB⊥PB，PA＝PB，
∴∠P＝360°﹣∠AOB﹣∠OAP﹣∠OBP＝360°﹣120°﹣90°﹣90°＝60°，
∴△PAB为等边三角形．
故答案为：等边三角形．
15．（3分）如图，在▱ABFE中，AB＝4，AE＝2，点E在⊙A上，O是▱ABFE的对称中心，O'是正方形ABCD的对称中心，若OO'＝d，则d的取值范围 1＜d＜3 ．
【解答】解：连接BE、DE、BD，
∵O是▱ABFE的对称中心，O'是正方形ABCD的对称中心，
∴O点在BE的中点处，O′在BD的中点处，
∴OO′是△BDE的中位线，
∴OO′＝DE，
在△AED中，由三角形三边关系得：AD﹣AE＜DE＜AD+AE，
∵AE＝2，AB＝AD＝4，
∴2＜DE＜6，
∴1＜OO′＜3．
故答案为：1＜d＜3．
三、解答题（本大题共8个小题，共75分）
16．（10分）解方程：
（1）x2+2x﹣1＝0；
（2）（2x﹣1）2＝4x﹣2．
【解答】解：（1）x2+2x﹣1＝0，
x2+2x+1＝2，
（x+1）2＝2，
x+1＝±，
x1＝﹣1﹣，x2＝﹣1+；
（2）（2x﹣1）2＝4x﹣2，
（2x﹣1）2﹣2（2x﹣1）＝0，
（2x﹣1）（2x﹣1﹣2）＝0，
（2x﹣1）（2x﹣3）＝0，
2x﹣1＝0或2x﹣3＝0，
x1＝，x2＝．
17．（9分）在平面直角坐标系中，△ABC的三个顶点都在边长均为1个单位长度的正方形网格的格点上．
（1）画出△ABC关于原点对称的图形△A1B1C1，并写出点C1的坐标；
（2）画出△ABC绕点O逆时针旋转90°后的图形△A2B2C2，并写出点B2的坐标；
（3）写出△A1B1C1经过怎样的旋转可直接得到△A2B2C2．
【解答】解：（1）如图，△A1B1C1即为所求；点C1的坐标（4，1）；
（2）如图，△A2B2C2即为所求；点B2的坐标（﹣3，﹣3）；
（3）△A1B1C1绕点O顺时针旋转90°后得到△A2B2C2．
18．（9分）已知关于x的一元二次方程x2+（2m+1）x+m﹣2＝0．
（1）求证：无论m取何值，此方程总有两个不相等的实数根；
（2）当该方程的判别式的值最小时，写出m的值，并求出此时方程的解．
【解答】（1）证明：∵Δ＝（2m+1）2﹣4×1×（m﹣2）
＝4m2+4m+1﹣4m+8
＝4m2+9＞0，
∴无论m取何值，此方程总有两个不相等的实数根；
（2）解：m＝0时，判别式的值最小，
把m＝0代入方程，
x2+x﹣2＝0，
（x+2）（x﹣1）＝0，
∴x＝﹣2或x＝1．
19．（9分）已知，如图，在△ABC中，∠ACB＝90°，请根据下列要求解决问题：
（1）利用尺规作出△ABC的内切圆⊙O；（不写作法，保留作图痕迹）
（2）若S△ABC＝6，内切圆⊙O的半径为1，求△ABC的周长．
【解答】解：（1）如图，分别作∠ACB和∠BAC的平分线，交于点O，
再过点O作AB的垂线，交AB于点D，
以点O为圆心，OD的长为半径画圆，
则⊙O即为所求．
（2）设⊙O与BC交于点E，与AC交于点F，连接OE，OF，OB，
∴OE⊥BC，OF⊥AC，
∵内切圆⊙O的半径为1，
∴OD＝OE＝OF＝1，
∴S△ABC＝S△AOB+S△BOC+S△AOC
＝
＝
＝
＝6，
∴AB+BC+AC＝12，
即△ABC的周长为12．
20．（9分）某商品的进价为每件30元，现在的售价为每件40元，每星期可卖出150件．市场调查反映：如果每件的售价每涨1元（售价每件不能高于45元），那么每星期少卖10件．设每件涨价x元（x为非负整数），每星期的销量为y件．
（1）求y与x的函数关系式及自变量x的取值范围；
（2）如何定价才能使每星期的利润最大且每星期的销量较大？每星期的最大利润是多少？
【解答】解：（1）由题意，y＝150﹣10x，0≤x≤5且x为非负整数；
（2）设每星期的利润为w元，
则w＝（40+x﹣30）y
＝（x+10）（150﹣10x）
＝﹣10（x﹣2.5）2+1562.5
∵x为非负整数，
∴当x＝2或3时，利润最大为1560元，
又∵销量较大，
∴x＝2，即当售价为42元时，每周的利润最大且销量较大，最大利润为1560元．
答：当售价为42元时，每星期的利润最大且每星期销量较大，每星期的最大利润为1560元．
21．（9分）已知，如图，在△ADC中，∠ADC＝90°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，∠BED＝2∠C．
（1）求证：BF是⊙O的切线；
（2）若BF＝FC，，求⊙O的半径．
【解答】（1）证明：连接OF．
∵∠OFB＝180°﹣∠B﹣∠BOF＝180°﹣∠B﹣2∠C＝180°﹣∠B﹣∠BED＝90°，
∴OF⊥BF，
∴BF是⊙O的切线；
（2）解：∵BF＝FC，
∴∠B＝∠FCB，
∵∠BED＝2∠C，
∴∠BDE+∠B＝3∠C＝90°，
∴∠B＝∠C＝30°，
∴∠AFE＝60°，∠BED＝60°，
∴△AEF是等边三角形，
则EF＝AE＝．
∴AD＝2．
又∵∠C＝30°，
∴CD＝6，
∴⊙O的半径是3．
22．（10分）在平面直角坐标系中，已知二次函数y＝﹣x2+bx+c的图象经过点（1，0）和（﹣3，0）．
（1）求二次函数的解析式，并写出此图象的顶点坐标；
（2）若点A（﹣2，y1），B（x2，y2）都在其图象上，且y1＞y2，则x2的取值范围是 x2＞0或x2＜﹣2 ；
（3）已知点P（m，m）与点Q均在该函数图象上（其中m＞0），且这两点关于该函数图象的对称轴对称，求m的值及点Q到x轴的距离．
【解答】解：（1）∵二次函数y＝﹣x2+bx+c的图象经过点（1，0）和（﹣3，0），
∴，解得，
∴抛物线解析式为：y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴顶点坐标为（﹣1，4）；
（2）抛物线的图象如图所示：
∵点A（﹣2，y1），B（x2，y2）都在其图象上，且y1＞y2，
∴x2＞0或x2＜﹣2；
故答案为：x2＞0或x2＜﹣2；
（3）∵点P（m，m）在该二次函数图象上，
∴m＝﹣m2﹣2m+3，
解得m＝，（m＞0，舍去负值），
∵P、Q两点关于抛物线对称轴对称，
∴点Q到x轴的距离为：．
23．（10分）如图①，在△ABC中，∠A＝90°，AB＝AC＝3，点D，E分别在边AB，AC上，，连接DE．将△ADE绕点A顺时针方向旋转，旋转角为α（0°＜α＜360°）．
（1）如图②，当α＝90°时，连接CE，BD，填空：CE与BD的数量关系为： CE＝BD ；CE与BD的位置关系为： CE⊥BD ；
（2）当0°＜α＜180°时，CE与BD交于点F，（1）中的结论还成立吗？若成立，请结合图③写出证明过程；若不成立，请说明理由；
（3）当△ADE旋转到ED⊥AC时，请直接写出BD的长．
【解答】解：（1）CE与BD的数量关系为：CE＝BD；CE与BD的位置关系为：CE⊥BD；
证明：∵AC＝AB，∠CAE＝∠BAD＝90°，AE＝AD，
∴△CAE≌△BAD（SAS），
∴∠ACE＝∠ABD，CE＝BD，
延长CE交BD于N，
∵∠AEC＝∠BEN，∠AEC＝∠BEN，∠ACE+∠AEC＝90°，
∴∠ABD+∠BEN＝90°，
∴∠BNE＝90°，
∴CE⊥BD；
故答案为：CE＝BD；CE⊥BD；
（2）（1）中的结论还成立，
证明：∵AC＝AB，∠CAE＝∠BAD＝90°，AE＝AD，
∴△CAE≌△BAD（SAS），
∴∠ACE＝∠ABD，CE＝BD，
∵AC＝AB，∠CAB＝90°，
∴∠ACB＝∠ABC，
∴∠ACB+∠ABC＝90°，
∴∠BCF+∠ABC+∠ABF＝90°，
∴∠BCF+∠CBF＝90°，
∴∠BFC＝90°，
∴CE⊥BD；
（3）如图4，延长CA交DE于H，
∵DE∥AB，
∴∠CAB＝∠AHE＝90°，
∴AH⊥DE，
∴AH＝HE＝DE，
∵DE＝AD＝2，
∴AH＝HE＝1，
∴CH＝3+1＝4，
∴BD＝CE＝＝；
如图5，过D作DH⊥AB于H，
∵DE∥AB，
∴∠BAD＝∠ADE＝45°，
∴AH＝DH＝AD＝1，
∴BH＝2，
∴BD＝＝，
综上所述，BD的长为或．