





初中北师大版第一章 三角形的证明1 等腰三角形教课内容ppt课件
展开1.了解等腰三角形中线、高线、角平分线的性质
2.掌握等边三角形的性质
2.用等腰、等边三角形的性质解决实际问题
上节课我们学习了等腰三角形,你能说出等腰三角形的性质吗?
等腰三角形的性质: (1)等腰三角形的两底角相等(等边对等角). (2)等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
试猜想等腰三角形的两底角的平分线、两腰上的高、两腰上的中线有什么关系呢?
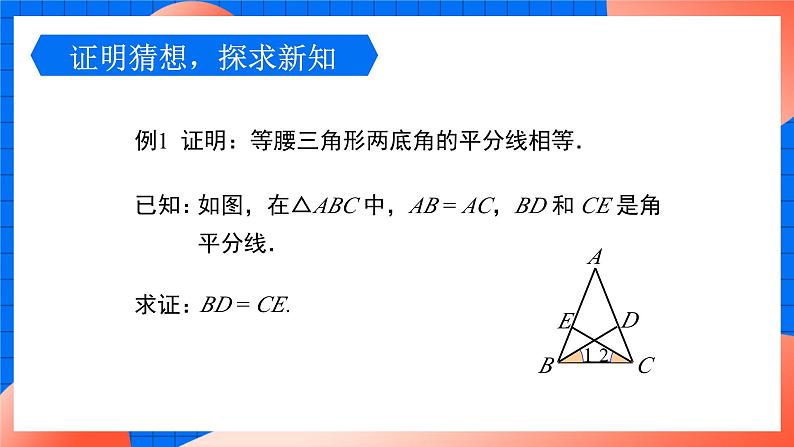
如图,在△ABC 中,AB = AC,BD 和 CE 是角平分线.
例1 证明:等腰三角形两底角的平分线相等.
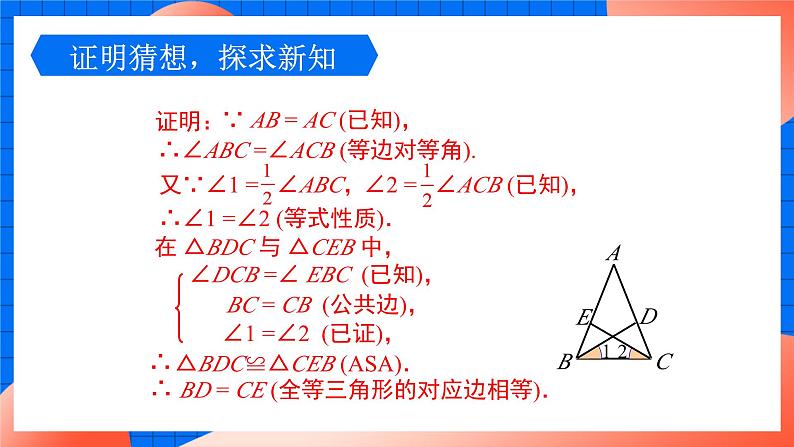
∵ AB = AC (已知),∴∠ABC =∠ACB (等边对等角).
∴∠1 =∠2 (等式性质).
在 △BDC 与 △CEB 中,
∠DCB =∠ EBC (已知),
BC = CB (公共边),
∠1 =∠2 (已证),
△BDC≌△CEB (ASA).
BD = CE (全等三角形的对应边相等).
例2 证明:等腰三角形两腰上的中线相等.
已知:如图,在△ABC 中, AB= AC,BD和CE是△ABC 的两腰上的中线. 求证:BD=CE.
证明: ∵ AB=AC, ∴ ∠ABC= ∠ACB(等边对等角).∵ BD和CE是△ABC两腰上的中线,∴CD= AC,BE= AB,∴CD= BE.在△BDC 和△CEB 中,∠ACB= ∠ABC, BC=CB,CD= BE ,∴ △BDC≌△CEB(SAS).∴ BD=CE(全等三角形的对应边相等).
例3 证明: 等腰三角形两腰上的高相等.
已知:如图,在 △ABC 中,AB = AC,BP,CQ 是 △ABC 两腰上的高.
∵ AB = AC (已知),∴∠QBC =∠PCB.
在△BQC 与△CPB 中,
∵∠BQC =∠CPB,∠QBC =∠PCB,BC = CB,
∴△BQC≌△CPB (AAS).
如果把等腰三角形两底角的平分线(二等分线)换成三等分线、四等分线,你能得到一个什么结论?如图.
2. 已知:如图,在△ABC 中,AB = AC.(1) 如果 AD = AC,AE = AB, 那么 BD = CE 吗? 为什么?
(2) 如果 AD = AC,AE = AB, 那么 BD = CE 吗? 为什么?
分别将等腰三角形底边两端点与腰上某一点相连,如果两条连线与底边所夹的角相等,那么这两条连线段相等.
两腰上和顶点等距的两点到对角顶点的距离相等.
等边三角形的三个内角都相等,并且每个角都等于60°.
想一想:等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?
已知:如图,在△ABC 中,AB = AC = BC.求证:∠A =∠B =∠C = 60°.
证明:在△ABC 中,∵ AB = AC (已知),∴∠B =∠C (等边对等角).同理∠A =∠B.又∵∠A +∠B +∠C = 180° (三角形的内角和等于180°),∴∠A =∠B =∠C = 60°.
定理: 等边三角形的三个内角都相等,并且每个角都等于 60°.
1.如图,△ABC 和△ADE 都是等边三角形,若△ABC 的周长为 18 cm,EC = 2 cm,则△ADE 的周长是 cm.
求等边三角形两条中线相交所成锐角的度数.
解:∵ BC= AC, CF是AB上的中线,∴∠BCF= ∠ABC(等腰三角形三线合一).在等边三角形ABC 中, ∠ABC =60°, ∴∠BCF=30°.同理, ∠CBE=30°.∴ ∠BOF=∠BCF+ ∠CBE=30°+30°= 60°.
已知: 如图,在等边三角形ABC 中,两条边上的中线BE,CF相交于点O.求:∠BOF的度数.
3.如图,在△ABC中,D,E是BC的三等分点,且△ADE是等边三角形,求∠BAC的度数.
解:∵ △ADE是等边三角形,∴ AD=DE=AE, ∠ADE= ∠DEA= ∠DAE =60°.∵ D,E是BC的三等分点,∴ BD=DE=EC,∴BD=AD,∴ ∠ABD= ∠BAD= 30°(三角形的外角性质).同理, ∠ ACE= ∠CAE= 30°.∴ ∠BAC= ∠BAD+ ∠DAE+ ∠BAD = 30°+ 60°+ 30° =120°.
等腰三角形两底角上的角平分线、两腰上的高、两腰上的中线的相关性质:底角的两条平分线相等;两条腰上的中线相等;两条腰上的高线相等.
教材第7页习题1.2第1,2,3题.
数学八年级下册1 等腰三角形精品课件ppt: 这是一份数学八年级下册1 等腰三角形精品课件ppt,文件包含112等边三角形的性质课件pptx、112等边三角形的性质教案doc等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
初中数学北师大版八年级下册1 等腰三角形教学演示课件ppt: 这是一份初中数学北师大版八年级下册1 等腰三角形教学演示课件ppt,共30页。PPT课件主要包含了创设情景激发兴趣,回顾定义引出新知,在等腰三角形中,底边另一边,顶角两腰的夹角,数学实验室,实践探索感受特征,实践探索感受交流,重合的角,重合的线段等内容,欢迎下载使用。
北师大版八年级下册1 等腰三角形图文ppt课件: 这是一份北师大版八年级下册1 等腰三角形图文ppt课件,共20页。PPT课件主要包含了探究新知,练习证明1,练习证明2,知识扩展,探究1,等边三角形,选一选,填一填,中考链接等内容,欢迎下载使用。














