第2章 直线与圆的位置关系小结 浙教版九年级数学下册课件

这是一份第2章 直线与圆的位置关系小结 浙教版九年级数学下册课件，共14页。
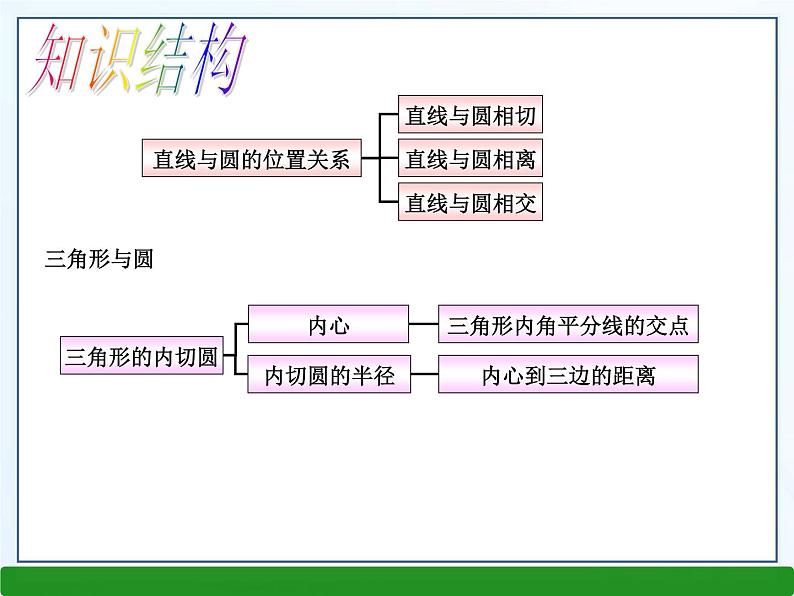
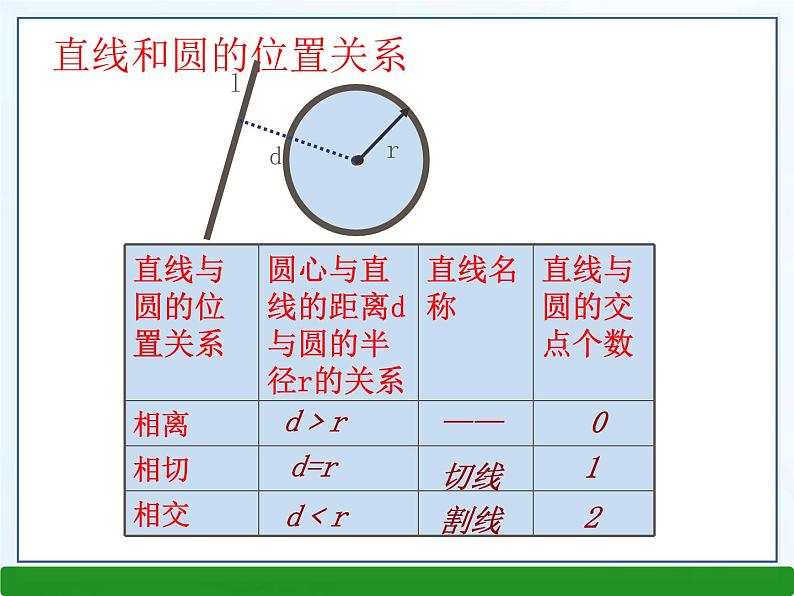
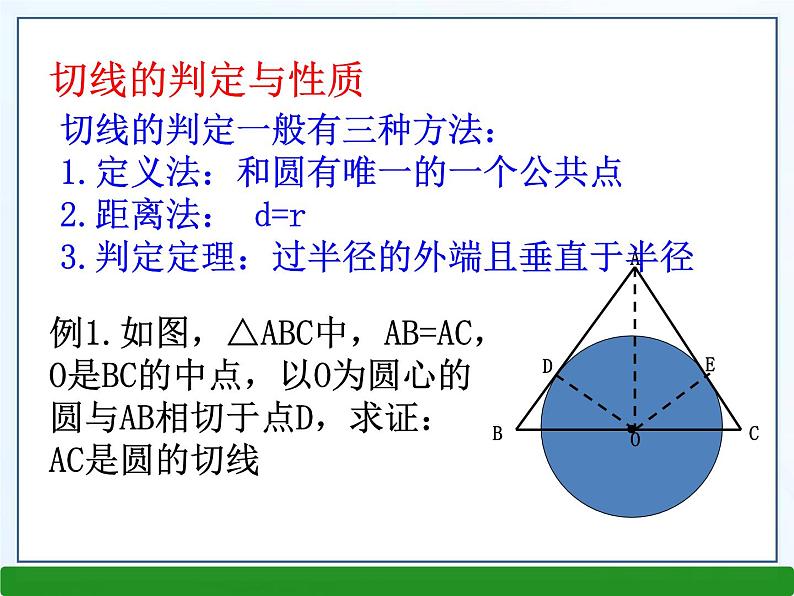
第二章 直线与圆的位置关系小 结直线与圆的位置关系直线与圆相切直线与圆相离直线与圆相交知识结构三角形的内切圆内心内切圆的半径三角形内角平分线的交点内心到三边的距离三角形与圆直线和圆的位置关系●ldrd﹥r——0d=r切线1d﹤r割线2切线的判定与性质例1.如图，△ABC中，AB=AC，O是BC的中点，以O为圆心的圆与AB相切于点D，求证：AC是圆的切线切线的判定一般有三种方法：1.定义法：和圆有唯一的一个公共点2.距离法： d=r3.判定定理：过半径的外端且垂直于半径切线长定理： 从圆外一点可以引圆的两条切线，它们的切线长相等。这一点和圆心的连线平分这两条切线的夹角。 从圆外一点引圆的切线，这个点与切点间的线段的长称为切线长。切线长：切线长及切线长定理三角形的内切圆1. Rt△ ABC三边的长为a、b、c，则内切圆的半径是r=______________2.外心到___________________的距离相等，是________________________的交点； 内心到______________________的距离相等,是_______________________的交点；3. 边长分别为3,4,5的三角形的内切圆半径与外接圆 半径的比为( ) A.1∶5 B.2∶5 C.3∶5 D.4∶5经典例题[解析] 连接BD，则在Rt△BCD中，BE＝DE，利用角的互余证明∠C＝∠EDC.例2：如图，已知Rt△ABC，∠ABC＝90°，以直角边AB为直径作⊙O，交斜边AC于点D，连接BD.(1)若AD＝3，BD＝4，求边BC的长；(2)取BC的中点E，连接ED，试证明ED与⊙O相切．[解析] 先由勾股定理求出AB，再利用相似求出BC.只要证明OD⊥DE就能说明ED与⊙O相切，利用直角三角形斜边上的中线等于斜边的一半得到等边转化为等角，进而算出∠ODE是直角．