浙教版八年级上册3.4 一元一次不等式组多媒体教学ppt课件

这是一份浙教版八年级上册3.4 一元一次不等式组多媒体教学ppt课件，共26页。PPT课件主要包含了教学目标，x+70×2，x＜7560，观察并思考，含有同一个未知数，是一元一次不等式，－1＜x≤2，x＞－1，x≤－2，同大取大等内容，欢迎下载使用。

1.理解一元一次不等式组的概念及不等式组的解的概念；2.会解由两个一元一次不等式组成的不等式组，并会用数轴确定解.
感受“化难为易”、化未知为已知的数学思想.
培养学生进行数学类比的能力.
1.不等式-x＞-2的解是( )A.x＞2 B.x＞-2 C.x＜2 D.x＜-2
2.不等式( )的解在数轴表示,如图所示:A.x＞-1 B.x＜-1 C.x≤-1 D.x≥-1
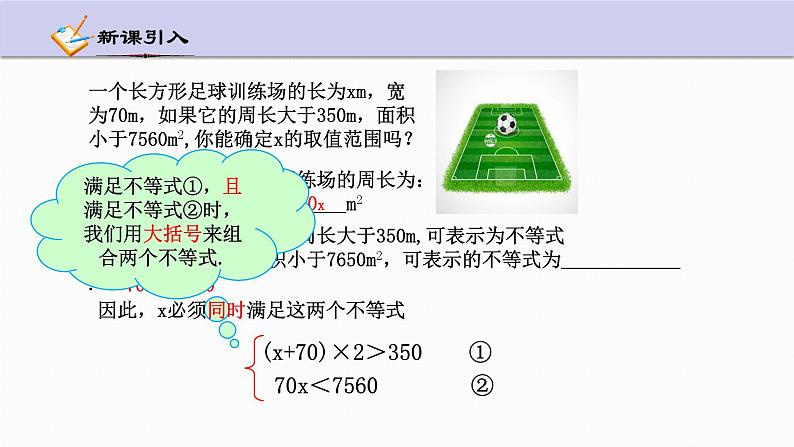
一个长方形足球训练场的长为xm，宽为70m，如果它的周长大于350m，面积小于7560m2,你能确定x的取值范围吗？
（1）这个长方形足球训练场的周长为： m,面积为 m2
（2）根据题中长方形的周长大于350m,可表示为不等式 ,面积小于7650m2，可表示的不等式为 .
(x+70)×2＞350
(x+70)×2＞350 ①
70x＜7560 ②
满足不等式①，且满足不等式②时，我们用大括号来组合两个不等式.
因此，x必须同时满足这两个不等式
不等式①和不等式②具有什么共同点？
一般地，有几个含同一未知数的一元一次不等式所组成的一组不等式，叫做一元一次不等式组.
1.下列式子中，哪些是一元一次不等式组？
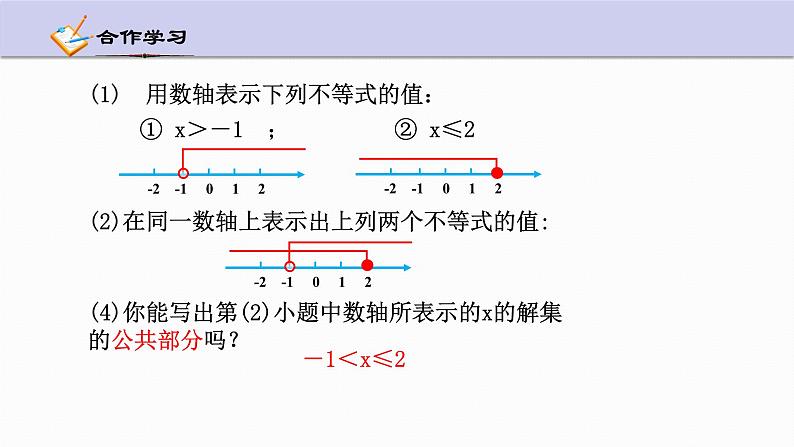
① x＞－1 ；　 ② x≤2
(1) 用数轴表示下列不等式的值：
(2)在同一数轴上表示出上列两个不等式的值:
(3)你能求出同时满足上述两个不等式的数解吗？
(4)你能写出第(2)小题中数轴所表示的x的解集的公共部分吗？
(5)请你写出下列数轴所表示的x的解集的公共部分.
没有公共部分，即无解.
通过以上练习，你发现了什么？
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
注: 当它们没有公共部分时,　则称这个不等式组无解.
利用数轴求下列不等式组的解集.
不等式组的解集是 x＞2
不等式组的解集是 x＜-2
不等式组的解集是 -1＜x＜2
解不等式①,得x＞-1
把①, ②两不等式的解表示在数轴上(如图)
所以原不等式组的解是 -1＜x≤6
根据一元一次不等式组解的意义, 只要求出各不等式的解的公共部分即可.
解一元一次不等式组的步骤:
（1）分别求出各不等式的解；
（2）将它们的解表示在同一数轴上；
（3）求原不等式组的解(即为它们解的公共部分).
把① ,②两个不等式的解表示在数轴上
1.解下列各一元一次不等式组：
2.若不等式组　 　的解为 x≥－b,　则下列各式正确的是　( ) A.a＞b B.a＜b C.b ≤a D.ab＞0
3.已知一元一次不等式x＞2和不等式组的解,求关于a的取值范围
4.解不等式组: 2－x＜x≤6－2x，并求出它的整数解.
6.已知关于x的不等式2(x-3)-a＜1的正整数解是1,2,3,求a的取值范围.
1.一元一次不等式组的概念
2.一元一次不等式组的解的概念
有几个含同一未知数的一元一次不等式所组成的一组不等式，叫做一元一次不等式组.
3.解一元一次不等式组的步骤
4.一元一次不等式组解集的规律