江西省赣州市2023年八年级上学期期末数学试题附答案

这是一份江西省赣州市2023年八年级上学期期末数学试题附答案，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．下列图形是轴对称图形的是（ ）
A．B．
C．D．
2．一种细菌的半径约为米，这个数用科学记数法表示为（ ）
A．B．C．D．
3．下列运算：①；②；③；④，其中结果正确的个数为（ ）
A．1B．2C．3D．4
4．一个多边形截去一个角后，得到的多边形的内角和为 ，那么原来的多边形的边数为（ ）．
A．12或13取14B．13或14C．12或13D．13或14或15
5．随着市场对新冠疫苗需求越来越大，为满足市场需求，某大型疫苗生产企业更新技术后，加快了生产速度，现在平均每天比更新技术前多生产10万份疫苗，现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间少用5天，设现在每天生产x万份，据题意可列方程（ ）
A．B．
C．D．
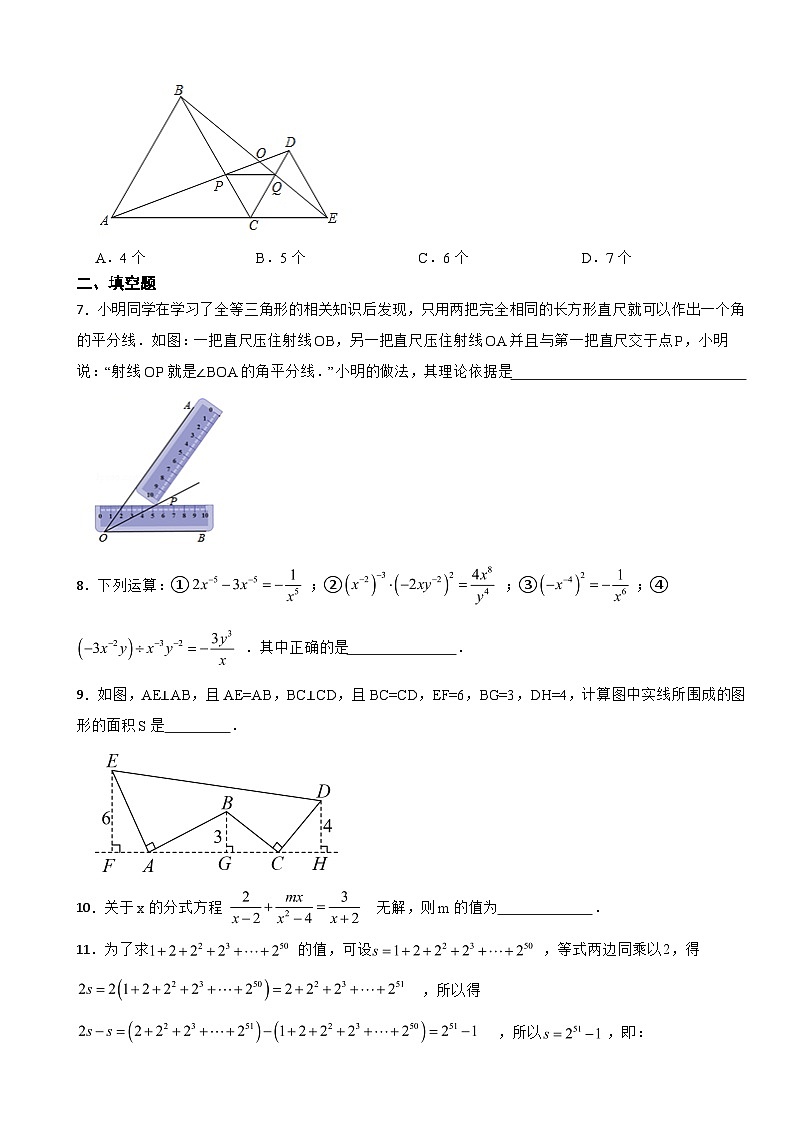
6．如图1，为线段上一动点（不与点、重合），在同侧分别作等边三角形和等边三角形，与交于点，与交于点，与交于点，连接．下列结论：①；②；③；④；⑤；⑥连接，平分；⑦为等边三角形．其中正确的有（ ）
A．4个B．5个C．6个D．7个
二、填空题
7．小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”小明的做法，其理论依据是
8．下列运算：①；②；③；④．其中正确的是 ．
9．如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，EF=6，BG=3，DH=4，计算图中实线所围成的图形的面积S是 ．
10．关于x的分式方程 无解，则m的值为 ．
11．为了求的值，可设，等式两边同乘以2，得，所以得，所以，即：．仿照以上方法求的值为 ．
12．在中，，．将一块足够大的直角三角尺（，）按如图所示放置，顶点在线段上滑动，三角尺的直角边始终经过点．并且与的夹角，斜边交于点．在点的滑动过程中，若是等腰三角形，则夹角的大小是 ．
三、解答题
13．如图，在中，点是延长线上一点，，，，求证：．
14．计算：
（1）
（2）（用简便方法计算）
15．先化简，再求值：，在，0，2这三个数中选一个你喜欢的代入求值．
16．如图，在平面直角坐标系中，的三个顶点的坐标分别为，，．
（1）作出关于轴对称的；
（2）直接写出的面积为 ；
（3）在轴上找一点，使最小．
17．如图，在中，，将沿着直线折叠，点落在点的位置，求的度数．
18．动点型问题是数学学习中的常见问题，解决这类问题的关键是动中求静，运用分类讨论及数形结合的思想灵活运用有关数学知识解决问题．如图，在直角三角形ABC中，∠ACB=90°，BC=4cm，AC=10cm，点D在射线CA上从点C出发向点A方向运动（点D不与点A重合），且点D运动的速度为2cm/s，设运动时间为x秒时，对应的△ABD的面积为ycm2．
（1）填写下表：
（2）在点D的运动过程中，出现△ABD为等腰三角形的次数有 ▲ 次，请用尺规作图，画出BD（保留作图痕迹，不写画法）；
（3）求当x为何值时，△ABD的面积是△ABC的面积的．
19．阅读理解：
例：已知：，求：和的值．
解：∵，
∴，
∴，
∴，，
∴，．
解决问题：
（1）若，求、的值；
（2）已知，，是的三边长且满足，
①直接写出 ， ．
②若是中最短边的边长（即；），且为整数，直接写出的值可能是 ．
20．班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动，基地离学校有90公里，队伍8：00从学校出发．苏老师因有事情，8：30从学校自驾小车以大巴1.5倍的速度追赶，追上大巴后继续前行，结果比队伍提前15分钟到达基地．问：
（1）大巴与小车的平均速度各是多少？
（2）苏老师追上大巴的地点到基地的路程有多远？
21．有足够多的长方形和正方形卡片，分别记为1号，2号，3号卡片，如图1所示．
（1）如果选取4张3号卡片，拼成如图2所示的一个正方形，请你用2种不同的方法表示阴影部分的面积．
①方法1： 方法2：
②请写出代数式，，这三个代数式之间的等量关系： ．
（2）解决问题：若，求的值．
（3）如果选取1张1号，2张2号，3张3号卡片，可拼成一个长方形（不重叠无缝隙），请画出这个拼出的长方形，根据图形的面积关系得到的等式是： ▲ ．
22．在中，与的角平分线交于点．
（1）①若，，则 ；
②若，，则 ．
（2）作的，的外角平分线，交于点，延长、交于点，请画出图形．
①若，，则 ▲ ，的形状为 ▲ ．
②若在中，存在一个内角等于另一个内角的2倍，请直接写出的度数．
23．已知点，，，且、满足．
（1）直接判断的形状；
（2）如图1，过点作射线（射线与边有交点），过点作于点，过点作于点，过点作的垂线交轴于点．
①求证：；②求点的坐标；
（3）如图2，点，为轴正半轴上的两点（在的上方），点在的延长线上，且满足，的延长线交轴于点，的角平分线交线段于点，若，请探究和的数量关系，并证明你的结论．
1．D
2．A
3．B
4．A
5．B
6．C
7．在角的内部，到角两边距离相等的点在角的平分线上
8．①②或②①
9．50
10．1或6或-4
11．
12．45°或90°或0°
13．解：，
，
在与中，
，
（SAS），
14．（1）解：
（2）解：
15．解：
，
∵，，
∴，，
代入，原式．
16．（1）解：如图，即为所求作的三角形，
（2）4
（3）解：如图，作点B关于x轴的对称点，连接交x轴于点，即为所求作的点，
由作图可得：
由两点之间线段最短可得此时最短.
17．解：如图，
由折叠的性质得：∠D=∠C=46°，
根据外角性质得：∠1=∠3+∠C，∠3=∠2+∠D，
则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+92°，
则∠1-∠2=92°．
故答案为：92°．
18．（1）解：∵CD=2x，AC=10，
∴AD=|10-2x|，
∴△ABD的面积为y=•AD•BC==．
当x=4时，y=|20-4×4|=cm2，
当x=6时，y=|20-4×6|=cm2；
（2）解：若△ABD为等腰三角形，只需AD=BD，AD=AB，或者AB=BD．
∵点D从C点出发，故当BD=AB时，AB、BD重合，不为三角形，
∴出现△ABD为等腰三角形的次数有2次；
作图如下：
（3）解：∵△ABC的面积为20，△ABD的面积是△ABC的面积的．
∴
解得：或x=．
19．（1）解：
解得：
（2）5；6；2，3，4
20．（1）解：设大巴的平均速度为x公里/时，则小车的平均速度为1.5x公里/时，根据题意，得： = + + 解得：x=40． 经检验：x=40是原方程的解，∴1.5x=60公里/时． 答：大巴的平均速度为40公里/时，则小车的平均速度为60公里/时
（2）解：设苏老师赶上大巴的地点到基地的路程有y公里，根据题意，得： + = 解得：y=30． 答：苏老师追上大巴的地点到基地的路程有30公里．
21．（1）；；
（2）解：

（3）解：选取1张1号，2张2号，3张3号卡片，可拼成一个长方形（不重叠无缝隙），
则长方形的面积为：
而
所以该长方形的边长为 如图所示：
该图形反映的面积恒等式为：
故答案为：
22．（1）；
（2）解：如图
①在△ABC中，，，则∠CBA=，
∴∠MAB=，∠NBA=；
∵AE平分∠MAB，BE平分∠NBA，
∴∠EAB=∠MAE，∠EBA=∠NBE，
∴∠EAB＋∠EBA=，
∴∠AEB=；
∠EBF=∠ABF＋∠ABE=，
∴△EBF为等腰直角三角形．
②由①可知，∠EBF==∠DAE，
当中，存在一个内角等于另一个内角的2倍时，△BEF为等腰直角三角形，
∴∠ABE=，
∴由四边形ADBE内角和，可得∠ADB=，
∴由（1）可得∠C=．
故答案为：．
23．（1）解：∵|a+4|+（a+b）2＝0．
∴a＝﹣4，b＝4，
∴点A（﹣4，0），B（0，4），
又∵点C（4，0），
∴OA＝OB＝OC＝4，AC＝OA+OC＝8，
∴∠OAB＝∠OBA＝∠OBC＝∠OCB＝45°，
∴AB＝BC，∠ABC＝90°，
∴△ABC是等腰直角三角形；
（2）解：①∵AD⊥l，CE⊥l，
∴∠ADB＝∠BEC＝90°＝∠ABC，
∴∠ABD+∠CBE＝90°，∠ABD+∠BAD＝90°，
∴∠BAD＝∠CBE，
又∵AB＝BC，∠ADB＝∠BEC，
∴△ABD≌△BCE（AAS），
∴AD＝BE；
②∵△ABD≌△BCE，
∴∠BAD＝∠CBE，
∴∠CAD＝∠FBE，
∵EF⊥CD，
∴∠EDC+∠DEF＝90°，
又∵∠DEF+∠CEF＝90°，
∴∠EDC＝∠CEF，
∴∠EDC+∠ADB＝∠CEF+∠BEC，
∴∠ADC＝∠BEF，
在△ADC和△BEF中，
，
∴△ADC≌△BEF（ASA），
∴BF＝AC＝8，则OF=4，
∴点F的坐标为（0，﹣4）；
（3）解：MN＝OH，
理由如下：如图2，在OP上截取PT＝PN，
∵MP平分∠APG，
∴∠APM＝∠GPM，
又∵PT＝PN，PM＝PM，
∴△MPT≌△MPN（SAS），
∴MN＝MT，∠ANP＝∠MTP，
∴∠GNH＝∠ATM，
∵GN＝GH，
∴∠GNH＝∠GHN，
∴∠GHN＝∠GNH＝∠MHK=∠ATM，
又∵∠MKH＝∠OKT，
∴∠KOT＝∠KMH＝90°，
∴∠AMT＝∠AOH＝90°，
又∵∠MAO＝∠MAO，AM＝AO，
∴△AMT≌△AOH（ASA），
∴MT＝OH，
∴MN＝OH．时间x秒
···
2
4
6
···
面积ycm2
···
12


···