初中数学人教版九年级下册27.2.1 相似三角形的判定备课课件ppt

这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定备课课件ppt，文件包含272教学课件相似三角形第4课时pptx、272教学设计相似三角形第4课时docx、272练习·基础巩固相似三角形第4课时docx、272练习·素能拓展相似三角形第4课时docx、272练习·能力提升相似三角形第4课时docx、272预习导学相似三角形第4课时docx等6份课件配套教学资源，其中PPT共19页， 欢迎下载使用。

　　三角形相似的判定方法有哪些？
　　（1）三个角分别相等，三条边成比例的两个三角形相似．
　　（2）平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似．
　　（3）三边成比例的两个三角形相似．
　　（4）两边成比例且夹角相等的两个三角形相似．
　　（5）两角分别相等的两个三角形相似．
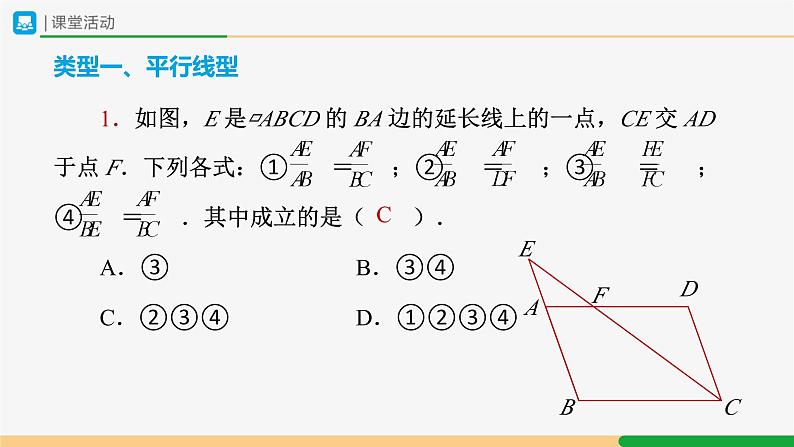
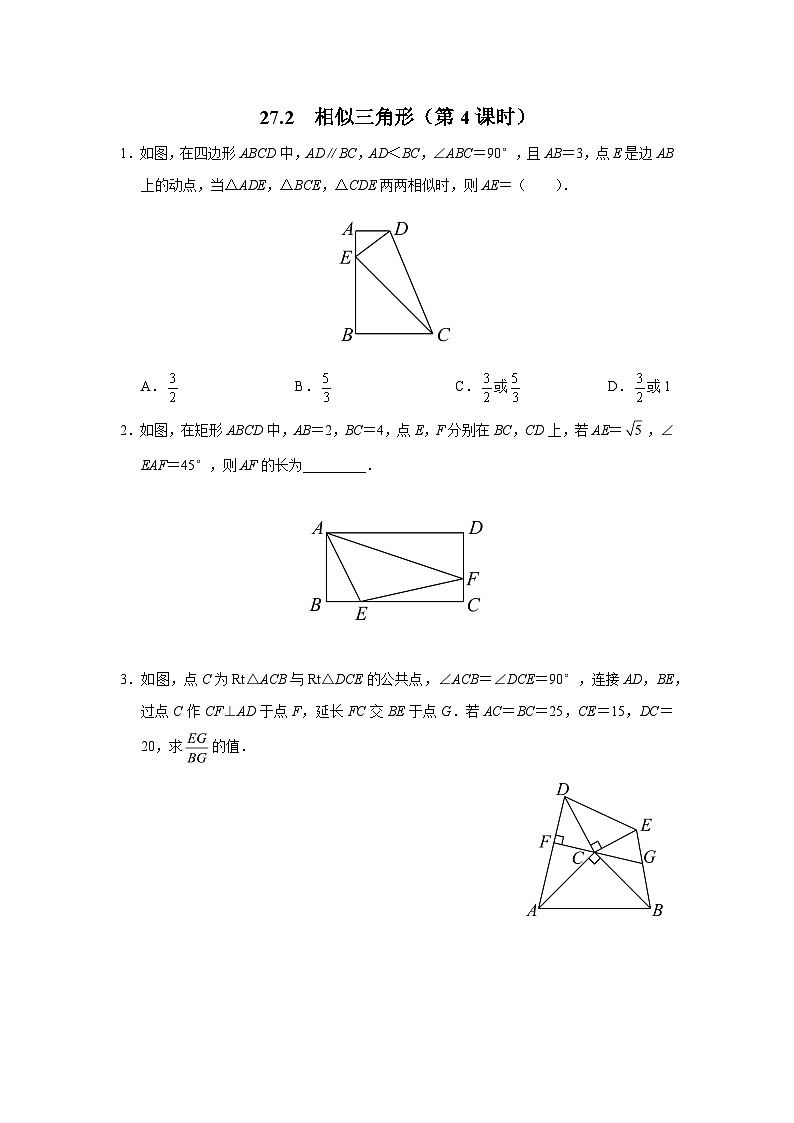
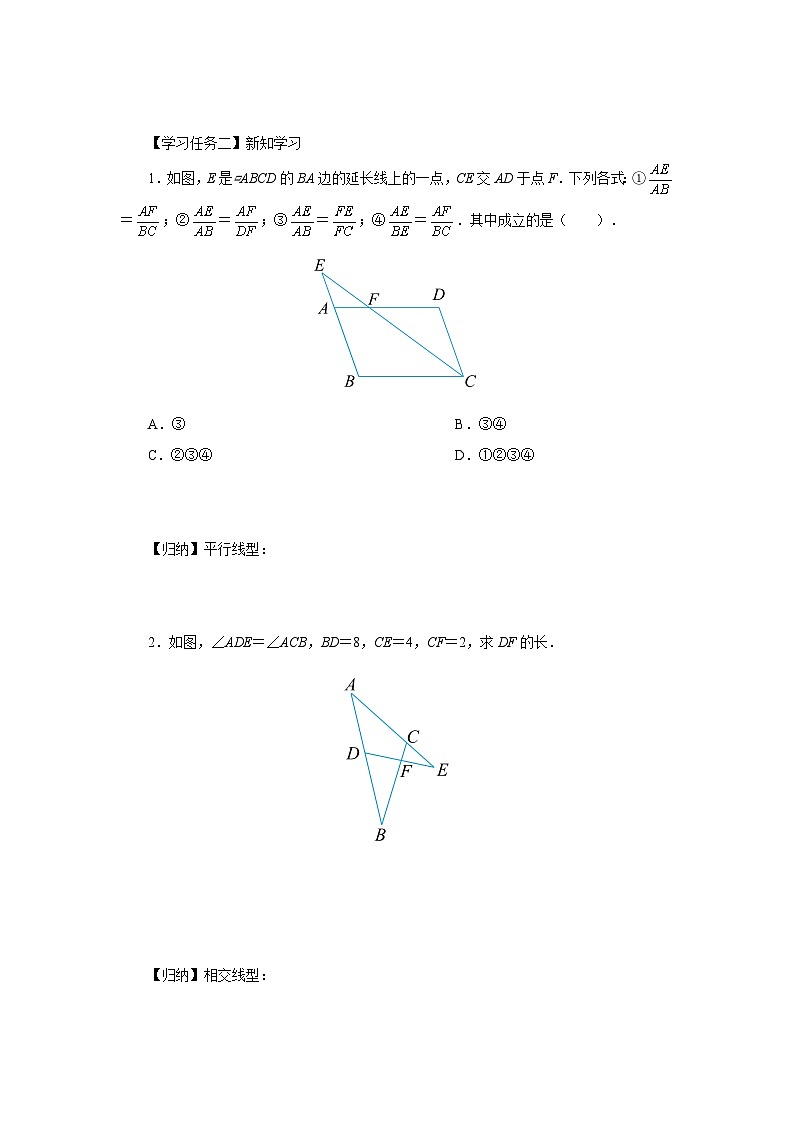
　　1．如图，E 是▱ABCD 的 BA 边的延长线上的一点，CE 交 AD于点 F．下列各式：① ＝ ；② ＝ ；③ ＝ ；④ ＝ ．其中成立的是（　　）．　　A．③B．③④　　C．②③④D．①②③④
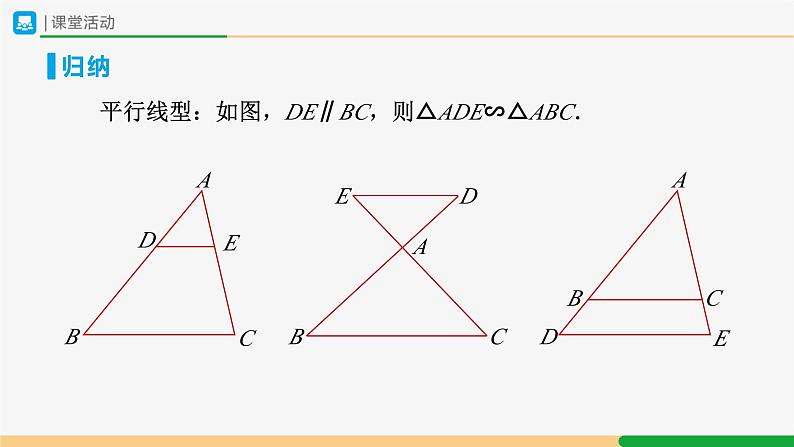
　　平行线型：如图，DE∥BC，则△ADE∽△ABC．
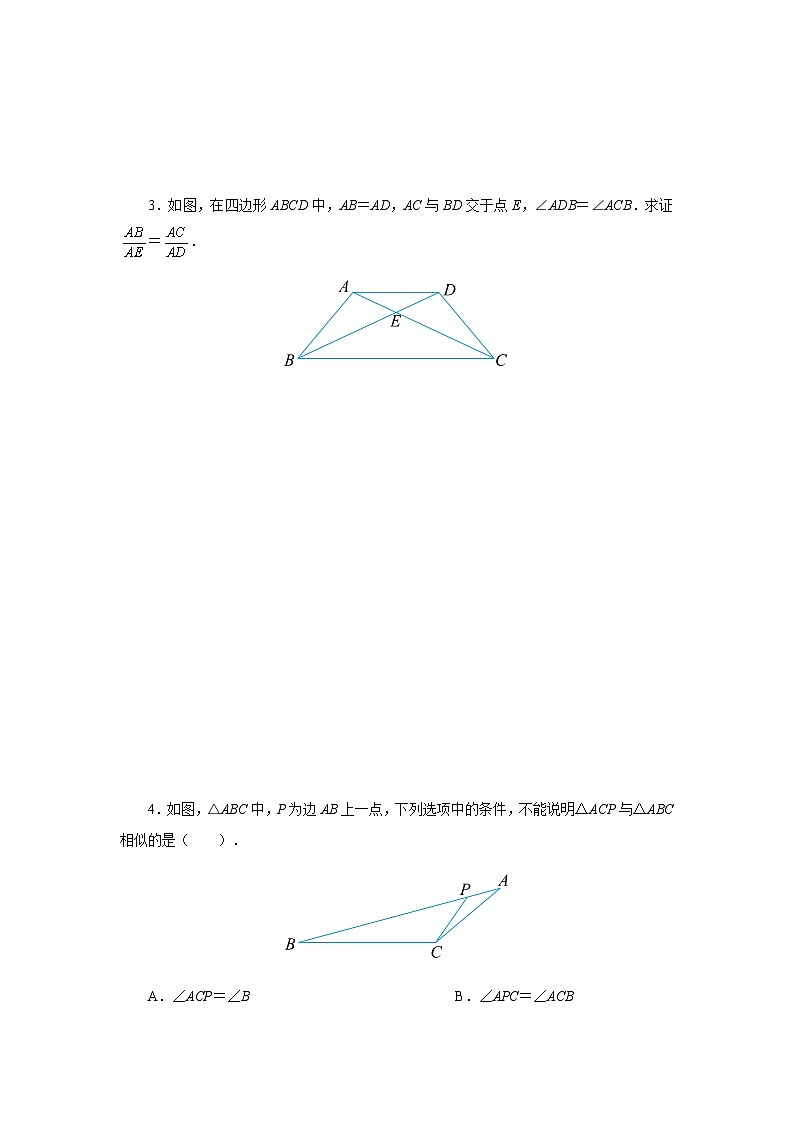
　　2．如图，∠ADE＝∠ACB，BD＝8，CE＝4，CF＝2，求 DF 的长．
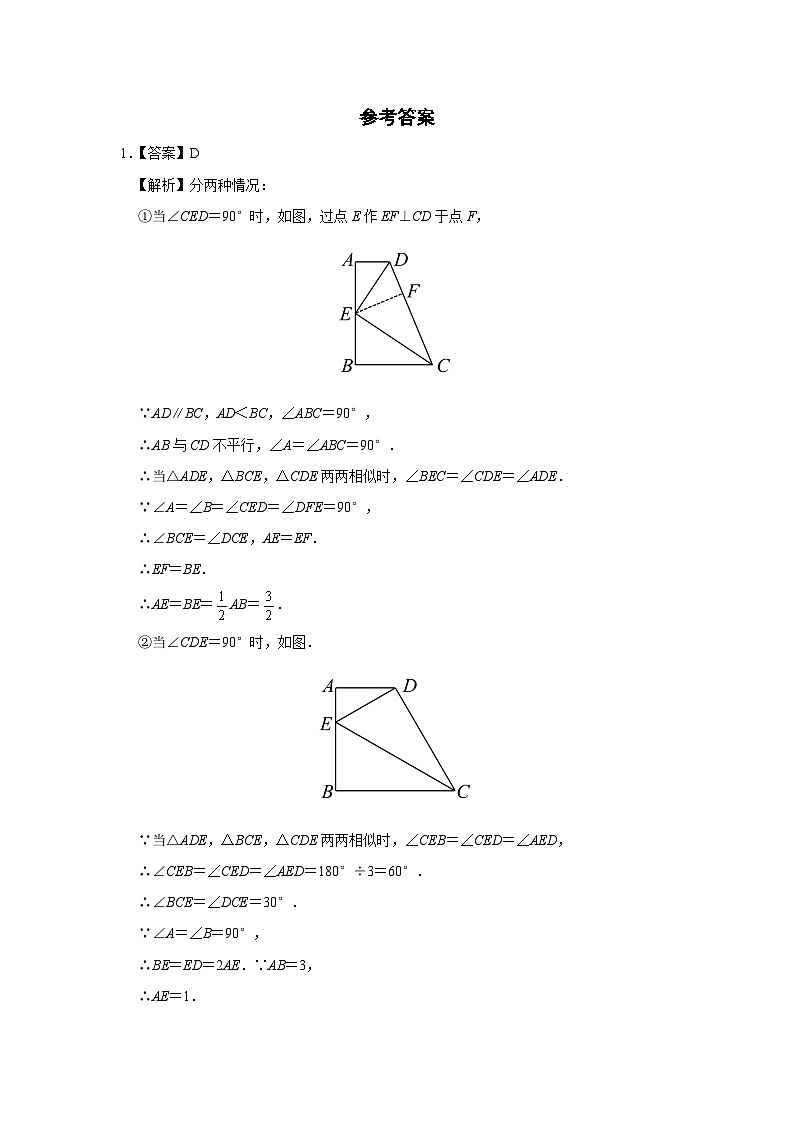
　　3．如图，在四边形 ABCD 中，AB＝AD，AC 与 BD 交于点 E，∠ADB＝∠ACB．求证 ＝ ．
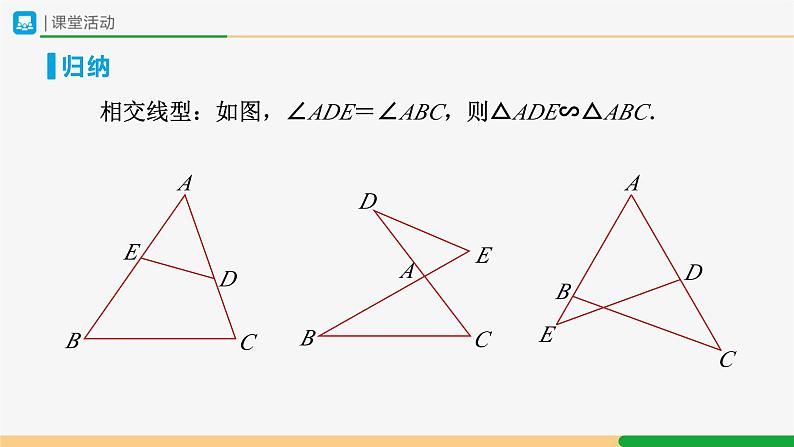
　　相交线型：如图，∠ADE＝∠ABC，则△ADE∽△ABC．
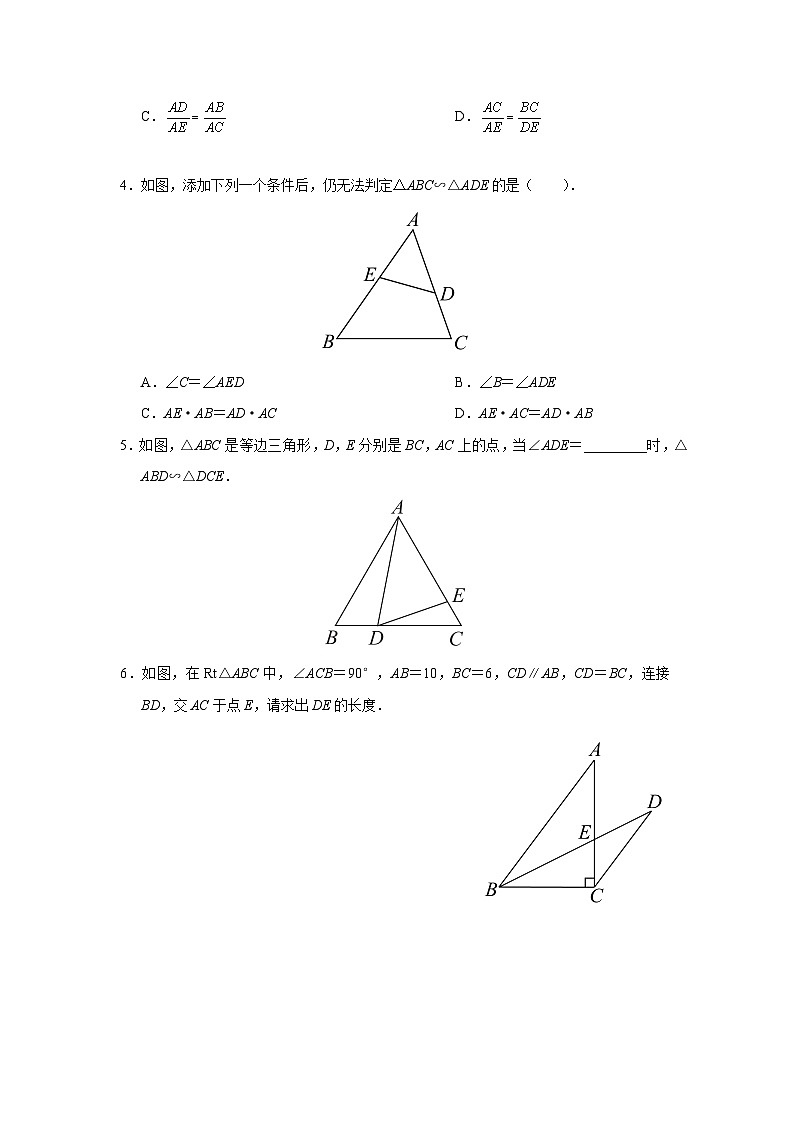
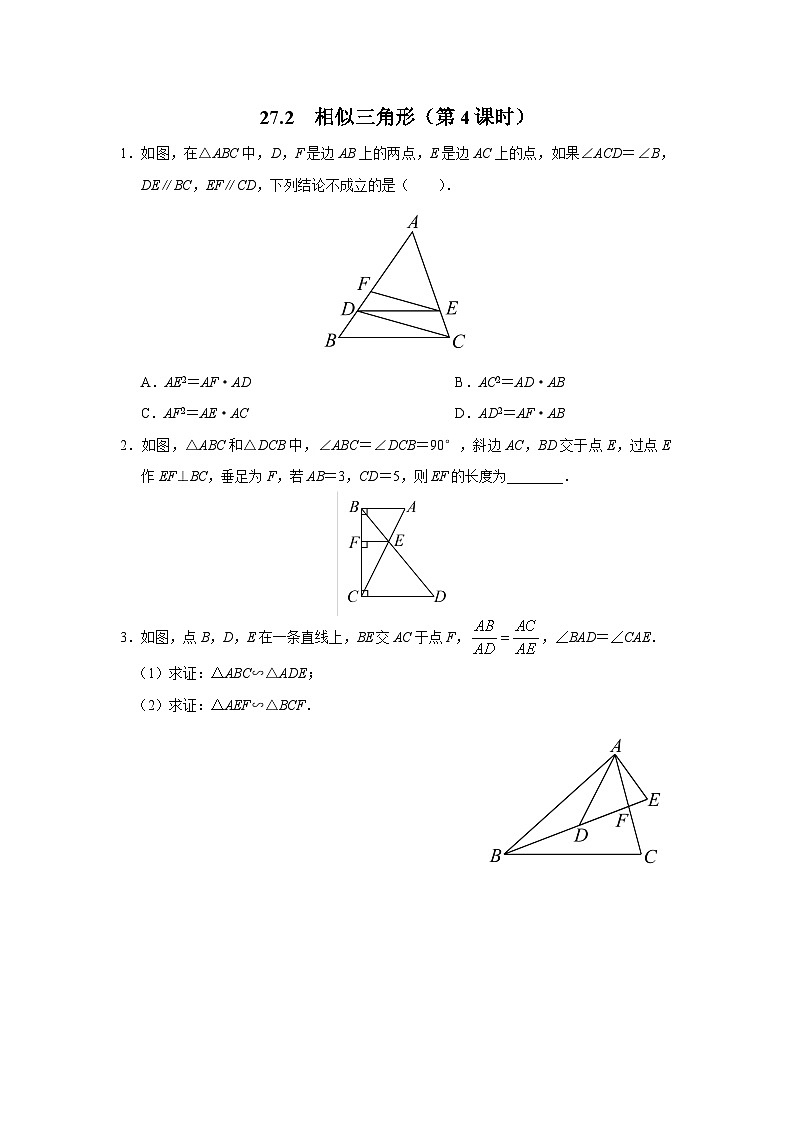
　　4．如图，△ABC 中，P 为边 AB 上一点，下列选项中的条件，不能说明△ACP 与△ABC 相似的是（　　）．　　A．∠ACP＝∠BB．∠APC＝∠ACB　　C．AC2＝AP·ABD．AB·CP＝AP·AC
　　5．如图，在△ABC 中，CD 是 AB 边上的高，且CD2＝AD·BD．　　（1）求∠ACB 的度数；
　　5．如图，在△ABC 中，CD 是 AB 边上的高，且CD2＝AD·BD．　　（2）若 AC＝4，AB＝10，求 AD 的长．
　　“子母”型：如图，∠ACD＝∠ABC，则△ACD∽△ABC．
　　6．如图，在△ABC 与△ADE 中， ＝ ，且∠EAC＝∠DAB．求证△ABC∽△ADE．
　　旋转型：如图，∠DAE＝∠BAC，∠ABC＝∠ADE，则△ADE∽△ABC．
　　如图，连接 BD，CE，则△ABD∽△ACE．
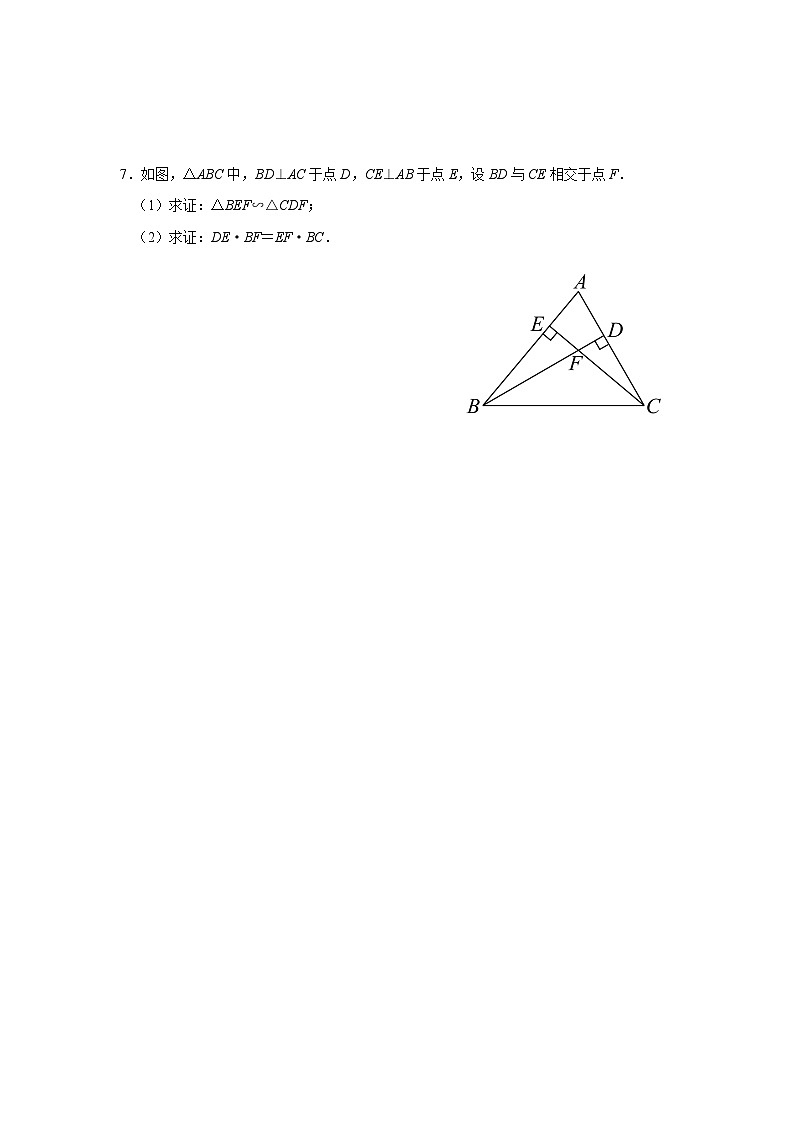
　　证明：如图，　　∵∠ADC＝∠1＋∠2＝∠B＋∠3，∠1＝∠B，　　∴∠2＝∠3．　　又AB＝AC，∴∠B＝∠C，　　∴△DCE∽△ABD．
　　7．如图，在△ABC 中，AB＝AC＝6，BC＝8，点 D 是 BC 边上的一个动点，点 E 在 AC 上，点 D 在运动过程中始终保持∠1＝∠B，求证△DCE∽△ABD．
　　一线三等角型：如图，在△ABC 和△CDE 中，B，C，D 三点共线，且∠B＝∠ACE＝∠D，则△ABC∽△CDE．
相似三角形判定的常见模型