第十九章 一次函数 单元复习课件 2023—2024学年人教版数学八年级下册

这是一份第十九章 一次函数 单元复习课件 2023—2024学年人教版数学八年级下册，共39页。

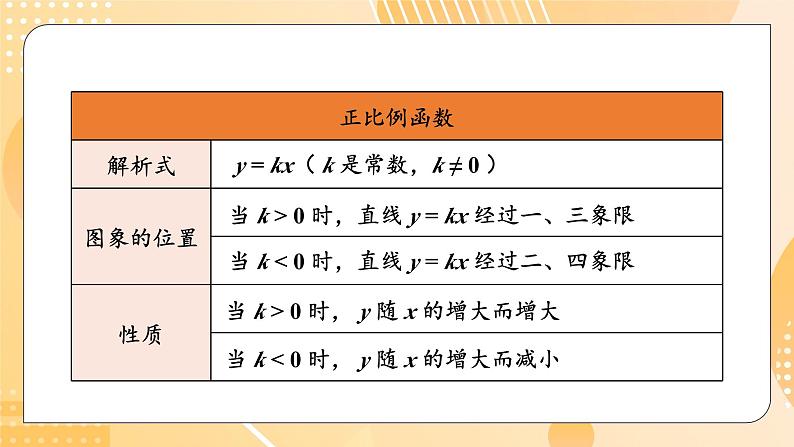
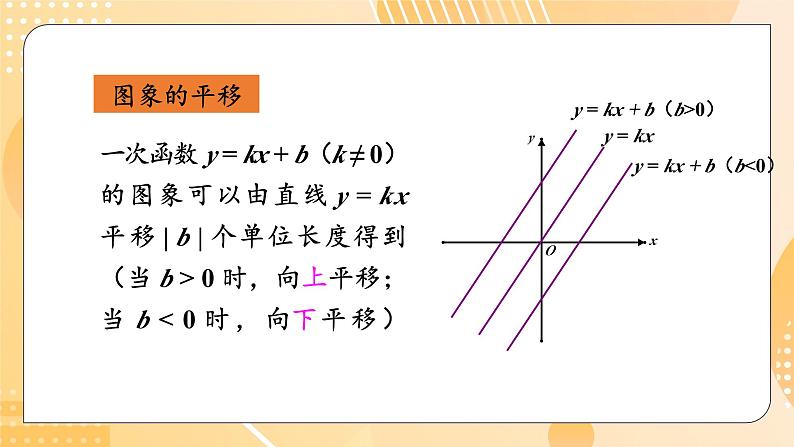
单元复习本章知识结构图变量函数常量、变量函数值、自变量函数的表示方法列表法图象法解析式法y = kx（ k 是常数，k ≠ 0 ）当 k > 0 时，直线 y = kx 经过一、三象限当 k < 0 时，直线 y = kx 经过二、四象限当 k > 0 时， y 随 x 的增大而增大当 k < 0 时， y 随 x 的增大而减小y = kx + b（ k，b 是常数，k ≠ 0 ）当 k > 0，b > 0 时，直线 y = kx 经过一、二、三象限当 k > 0，b < 0 时，直线 y = kx 经过一、三、四象限当 k < 0，b > 0 时，直线 y = kx 经过一、二、四象限当 k < 0，b < 0 时，直线 y = kx 经过二、三、四象限当 k > 0 时， y 随 x 的增大而增大当 k < 0 时， y 随 x 的增大而减小一次函数 y = kx + b（k ≠ 0）的图象可以由直线 y = kx 平移 | b | 个单位长度得到（当 b > 0 时，向上平移；当 b < 0 时，向下平移）y = kxy = kx + b（b>0）y = kx + b（b<0）图象的平移一次函数与方程、不等式实际应用一次函数与一元一次方程一次函数与一元一次不等式一次函数与二元一次方程（方程）简单应用、确定最值和最佳方案1. 小亮现已存款 100 元，他计划今后三年每月存款 10 元. 存款总金额 y（单位:元）将随时间x（单位:月）的变化而改变．指出其中的常量与变量，自变量与函数，并写出函数解析式.解: 函数解析式 y = 10x + 100（0 ≤ x ≤ 36，x为整数），其中常量是 10，100，变量是存款总数 y 与时间 x，自变量是时间 x，函数是存款总数 y.【选自教材P107 第1题】复习巩固2. 判断下列各点是否在直线 y = 2x + 6上. 这条直线 与坐标轴交于何处？解: 当 x = -5 时，y = 2×(-5) + 6 = -4.当 x = -7 时，y = 2×(-7) + 6 = -8 ≠ 20；【选自教材P107 第2题】这条直线与坐标轴交于点（0,6），（-3,0）.2. 判断下列各点是否在直线 y = 2x + 6上. 这条直线 与坐标轴交于何处？【选自教材P107 第2题】3. 填空：（1）直线 经过第_______________象限，y 随 x 的增大而_______；（2）直线 y = 3x - 2 经过第_______________象限，y 随 x 的增大而_______.一、二、四减小一、三、四增大【选自教材P107 第3题】4. 根据下列条件分别确定函数 y = kx + b 的解析式: （1）y 与 x 成正比例，当 x = 5 时，y = 6；【选自教材P107 第4题】5. 试根据函数 y = 3x-15 的性质或图象，确定 x 取何值时: （1）y > 0； （2）y < 0.解:在平面直角坐标系中画出函数 y = 3x -15 的图象:（1）由图象知，当 x > 5 时，直线在 x 轴的上方，即此时 y > 0，所以当 x > 5 时，y > 0；【选自教材P107 第5题】5. 试根据函数 y = 3x-15 的性质或图象，确定 x 取何值时: （1）y > 0； （2）y < 0.（2）由图象知，当 x < 5 时，直线在 x 轴的下方，即此时 y < 0，所以当 x < 5 时，y < 0.【选自教材P107 第5题】6. 在某火车站托运物品时，不超过 1 kg 的物品需付 2 元，以后每增加 1 kg（不足 l kg 按 1 kg 计）需增加托运费0.5元. 设托运 p kg（p 为整数）物品的费用为 c 元. 试写出 c 的计算公式.【选自教材P107 第6题】综合运用综合运用6. 在某火车站托运物品时，不超过 1 kg 的物品需付 2 元，以后每增加 1 kg（不足 l kg 按 1 kg 计）需增加托运费0.5元. 设托运 p kg（p 为整数）物品的费用为 c 元. 试写出 c 的计算公式.【选自教材P107 第6题】7. 某水果批发市场规定，批发苹果不少于 100 kg 时，批发价为 2.5元/kg. 小王携带现金 3 000 元到这市场采购苹果，并以批发价买进．设购买的苹果为 x kg，小王付款后还剩余现金 y 元. 试写出 y 关于 x 的函数解析式，并指出自变量 x的取值范围.求自变量的取值范围1. 批发苹果不少于 100 kg ，2. y ≥ 0.【选自教材P107 第7题】解: y 与 x 之间的函数解析式为 y = 3 000 - 2.5x ，因为剩余现金 y ≥ 0，所以 3 000-2.5x ≥ 0，所以 x ≤ 1 200，所以自变量 x 的取值范围是 100 ≤ x ≤ 1 200.7. 某水果批发市场规定，批发苹果不少于 100 kg 时，批发价为 2.5元/kg. 小王携带现金 3 000 元到这市场采购苹果，并以批发价买进．设购买的苹果为 x kg，小王付款后还剩余现金 y 元. 试写出 y 关于 x 的函数解析式，并指出自变量 x的取值范围.【选自教材P107 第7题】8. 匀速地向一个容器内注水，最后把容器注满．在注水过程中，水面高度 h 随时间 t 的变化规律如图所示（图中 OABC 为一折线）. 这个容器的形状是下图中哪一个？匀速地向另两个容器注水时，你能画出水面高度 h 随时间 t 变化的图象（草图）吗？【选自教材P108 第8题】解:从图象上看，在注水过程中，容器的中间部分的水面高度 h 随时间 t 的变化最缓慢，其次是容器的下面部分，变化最迅速的应该是容器的上面部分，因此可以断定这个容器的形状是图（3）.（1）向图（1）的容器注水时水面高度 h 随时间 t 变化的图象:（2）向图（2）的容器注水时水面高度 h 随时间 t 变化的图象:9. 已知等腰三角形周长为 20.（1）写出底边长 y 关于腰长 x 的函数解析式（x 为自变量）；（2）写出自变量取值范围；（3）在直角坐标系中，画出函数图象.解:（1）因为2x + y = 20，所以 y = 20 - 2x. 所以底边长 y 与腰长 x 之间的函数关系式为 y = 20 - 2x.【选自教材P108 第9题】9. 已知等腰三角形周长为 20.（1）写出底边长 y 关于腰长 x 的函数解析式（x 为自变量）；（2）写出自变量取值范围；（3）在直角坐标系中，画出函数图象.（2）因为三角形任意两边之和要大于第三边，解得 5 < x < 10，即自变量 x 的取值范围是 5 < x < 10.【选自教材P108 第9题】（3）图象如图所示.9. 已知等腰三角形周长为 20.（1）写出底边长 y 关于腰长 x 的函数解析式（x 为自变量）；（2）写出自变量取值范围；（3）在直角坐标系中，画出函数图象.【选自教材P108 第9题】10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （1）求 S 关于 x 的函数解析式； （2）求 x 的取值范围； （3）当 S = 12 时，求 P 点坐标； （4）画出函数 S 的图象.【选自教材P108 第10题】利用三角形的面积求一次函数的解析式，关键是要找到合适的底和高.解:（1）因为动点 P(x，y) 在第一象限，所以 x > 0，y > 0.因为 x + y = 10，所以 y = 10 - x ， 所以 ，即 S 关于 x 的函数解析式为 S = -4x + 40； 10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （1）求 S 关于 x 的函数解析式；【选自教材P108 第10题】10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （2）求 x 的取值范围； （3）当 S = 12 时，求 P 点坐标；（2）因为点 P 在第一象限内，所以 x 的取值范围是0 < x < 10；（3）当 S = 12 时，-4x + 40 = 12，x = 7，则 y = 10-x = 3，所以当 S = 12 时，P 点的坐标为（7，3）.【选自教材P108 第10题】10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （4）画出函数 S 的图象.（4）函数 S 的图象如图所示:【选自教材P108 第10题】11.（1）画出函数 y = | x -1 | 的图象. （2）设 P(x,0) 是 x 轴上的一个动点，它与 x 轴上表示-3 的点的距离为 y. 求 y 关于 x 的函数解析式，并画出 这个函数的图象.【选自教材P108 第11题】11.（1）画出函数 y = | x -1 | 的图象. （2）设 P(x,0) 是 x 轴上的一个动点，它与 x 轴上表示-3 的点的距离为 y. 求 y 关于 x 的函数解析式，并画出 这个函数的图象.（2） y = | x - ( -3) | = | x + 3 | = 这个函数的图象如图所示：x + 3（x ≥ -3），-x -3（x < -3），【选自教材P108 第11题】12. A，B 两地相距 25 km. 甲 8:00 由 A 地出发骑自行车去 B 地，速度为 10 km/h；乙 9:30 由 A 地出发乘汽车也去 B 地，速度为40 km/h. （1）分别写出两个人的行程关于时刻的函数解析式； （2）乙能否在途中超过甲？如果能超过，何时超过？【选自教材P108 第12题】这题是行程问题，由于是以平均速度考虑问题，因此两人的运动形式都按匀速运动考虑.解:（1）设甲、乙行驶中的时刻为 x 时，甲、乙行驶的路程分别为 y甲，y乙，则有 y甲 = 10(x-8) = 10x-80 (8 ≤ x ≤ 10.5)，y乙= 40(x - 9.5) = 40x - 380 (9.5≤ x ≤ 10.125)；（2）令 y甲< y乙，则10x-80 < 40x-380. 所以 x > 10，即 10 时以后乙超过甲.12. A，B 两地相距 25 km. 甲 8:00 由 A 地出发骑自行车去 B 地，速度为 10 km/h；乙 9:30 由 A 地出发乘汽车也去 B 地，速度为40 km/h. （1）分别写出两个人的行程关于时刻的函数解析式； （2）乙能否在途中超过甲？如果能超过，何时超过？【选自教材P108 第12题】一个有进水管与出水管的容器，从某时刻开始 4 min 内只进水不出水，在随后的 8 min 内既进水又出水，每分的进水量和出水量是两个常数.容器内的水量 y（单位:L）与时间 x（单位:min）之间的关系如图所示. （1）当 0 ≤ x ≤ 4 时，求 y 关于 x 的函数解析式.（2）当 4 < x ≤ 12 时，求 y 关于 x 的函数解析式.（3）每分进水、出水各多少升？【选自教材P108 第13题】拓广探索解:（1）设 y 关于 x 的函数解析式为 y = kx (0 ≤ x ≤ 4).由题意知 20 = 4k，解得 k = 5. 所以当 0 ≤ x ≤ 4 时，y 关于 x 的函数解析式为 y = 5x. （1）当 0 ≤ x ≤ 4 时，求 y 关于 x 的函数解析式.（2）当 4 < x ≤ 12 时，求 y 关于 x 的函数解析式.（2）设 y 关于 x 的函数解析式为 y = k'x + b' ( 4< x ≤ 12 ).（3）每分进水、出水各多少升？一次越野赛跑中，当小明跑了 1600 m 时，小刚跑了1 450 m. 此后两人分别以 a m/s 和 b m/s 匀速跑. 又过100 s 时小刚追上小明，200 s 时小刚到达终点，300 s 时小明到达终点．这次越野赛跑的全程为多少米？解: 根据题意得方程组:所以 1600 + 300×1.5 = 2050 (m)，即这次越野赛跑的全程为 2050 m.【选自教材P109 第14题】A 城有肥料 200 t，B 城有肥料 300 t. 现要把这些肥料全部运往 C，D 两乡.从 A 城往 C，D 两乡运肥料的费用分别为 20 元/t 和 25 元/t；从 B 城往 C，D 两乡运肥料的费用分别为 15 元/t 和 24 元/t. 现 C 乡需要肥料 240 t，D 乡需要肥料 260 t，怎样调运可使总运费最少？【选自教材P109 第15题】解:设 A 城运往 C 乡x t 肥料，总费用为 y 元，由题意列方程得 y = 20x + ( 200-x)×25 + (240-x )×15 + (300-240 + x )×24 (0 ≤ x ≤ 200)，整理得 y = 4x + 10040 ( 0 ≤ x ≤ 200 )，当 x = 0 时，y最小，y最小值 = 10 040.答:调运方案为 A 城运往 D 乡 200 t 肥料，B 城运往 D 乡60 t肥料，B 城运往 C乡 240 t 肥料，可使总费用最小.