资料中包含下列文件,点击文件名可预览资料内容




还剩33页未读,
继续阅读
所属成套资源:2023年浙教版数学八年级上册 全套同步能力测试卷
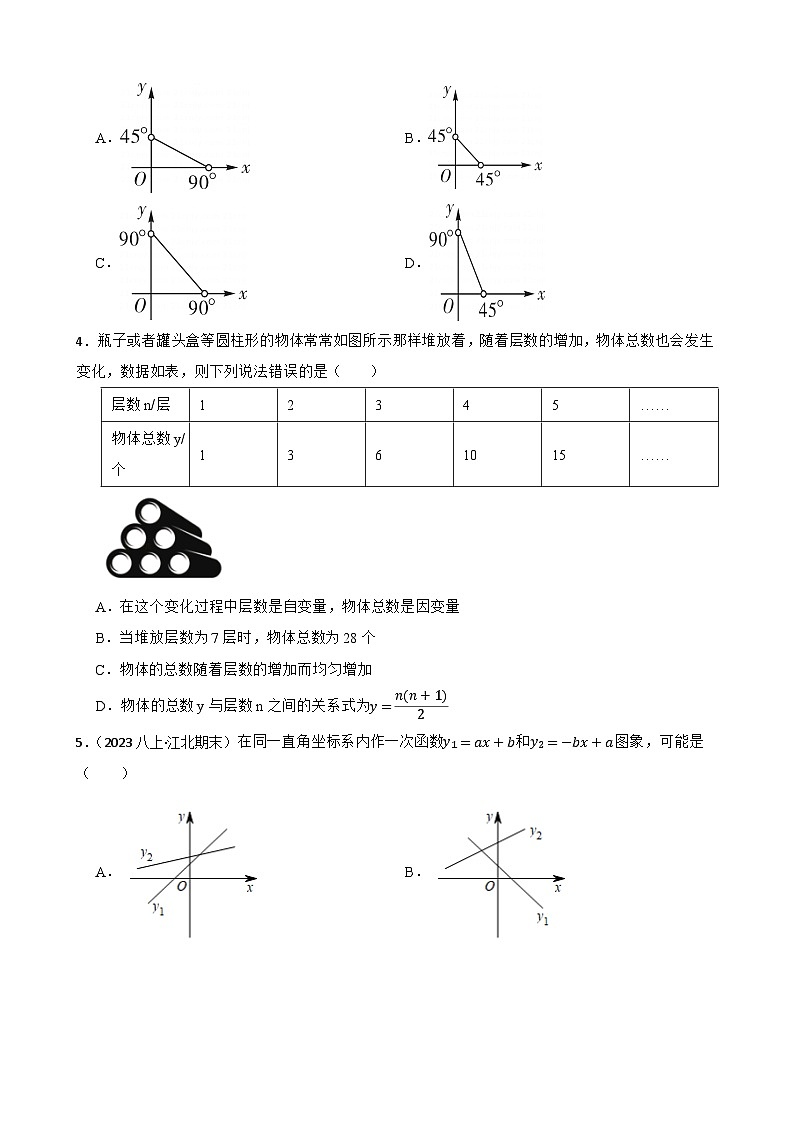
成套系列资料,整套一键下载
【精品解析】2023年浙教版数学八年级上册第五章 一次函数 单元测试(B卷)
展开
这是一份【精品解析】2023年浙教版数学八年级上册第五章 一次函数 单元测试(B卷),文件包含2023年浙教版数学八年级上册第五章一次函数单元测试B卷教师版docx、2023年浙教版数学八年级上册第五章一次函数单元测试B卷学生版docx等2份试卷配套教学资源,其中试卷共72页, 欢迎下载使用。
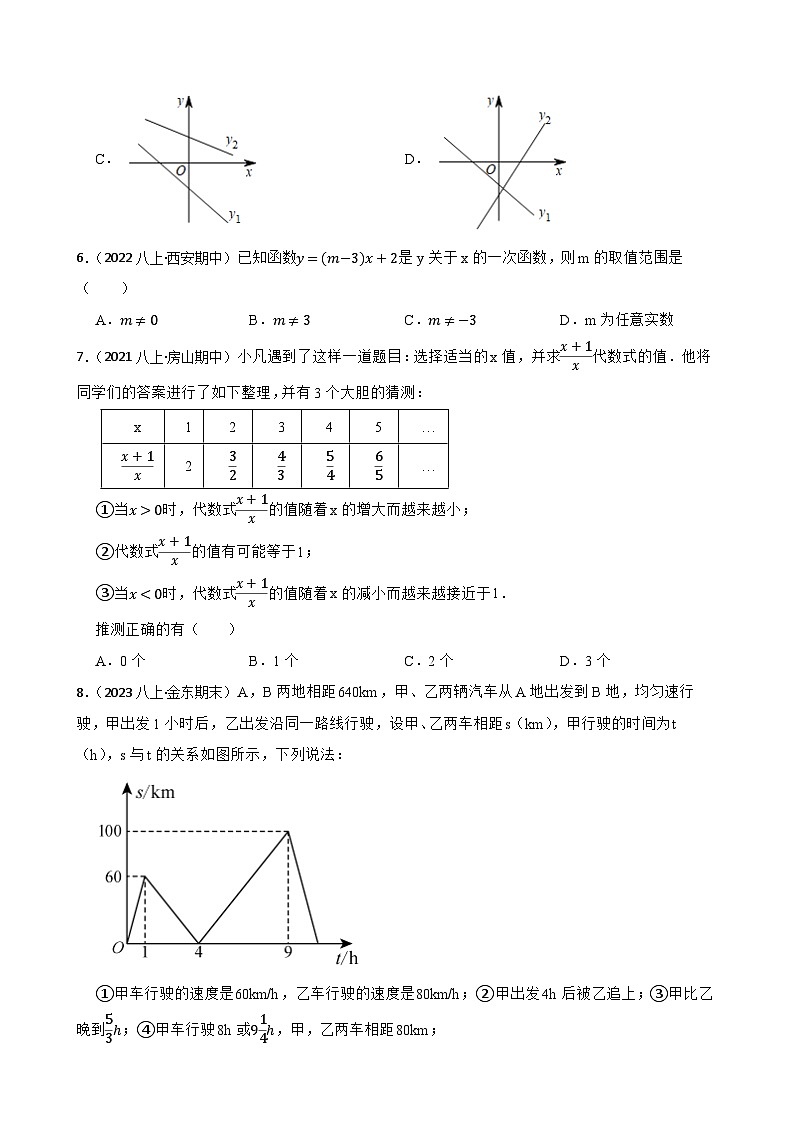
2023年浙教版数学八年级上册第五章 一次函数 单元测试(B卷)一、选择题(每题3分,共30分)1.弹簧挂重物会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)有下面的关系. 下列说法不正确的是( )A.x与y都是变量,x是自变量,y是因变量B.所挂物体为6kg,弹簧长度为11cmC.物体每增加1kg,弹簧长度就增加0.5cmD.挂30kg物体时一定比原长增加15cm【答案】D【知识点】常量、变量【解析】【解答】解:由表格可得到,x与y都是变量,x是自变量,y是因变量;物体每增加1kg,弹簧长度就增加0.5cm;所挂物体为6kg,弹簧长度为8+0.5×6=11cm;挂30kg物体时长为8+15>20,不符合已知条件。故选项D错误。 故答案为:D。 【分析】由表格可知:所挂物体每增加1kg,弹簧就伸长0.5cm,据此逐个判断即可。2.(2020八上·烈山期中)下列各列表中,不能表示y是x的函数的是( ) A. B.C. D.【答案】C【知识点】函数的概念【解析】【解答】解:A、B、D对于每个x,都有唯一的y值与之对应,故y是x的函数;C中x=2时,有2个不同的函数值,故y不是x的函数;故答案为:C.【分析】根据函数的定义对选项一一判断即可。3.(2023八上·宁波期末)在直角三角形ABC中,∠C=90∘,∠A=x,∠B=2y,则y与x之间的函数关系式是( )A. B.C. D.【答案】A【知识点】用图象表示变量间的关系【解析】【解答】解:∵在Rt△ABC中,∠C=90°,∠A=x,∠B=2y, ∴∠A+∠B=90°,即x+2y=90°, ∴y=-12x+45° 当x=0°时,y=45°, 当y=0时,x=90°, ∴函数y=-12x+45°与x轴和y轴的交点坐标分别为(90°,0),(0,45°). 故答案为:A. 【分析】根据直角三角形两锐角互余可得∠A+∠B=90°,即可表示出函数关系式为y=-12x+45°,进而求出其与x轴和y轴的交点坐标,即可判断得出结论.4.瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )A.在这个变化过程中层数是自变量,物体总数是因变量B.当堆放层数为7层时,物体总数为28个C.物体的总数随着层数的增加而均匀增加D.物体的总数y与层数n之间的关系式为y=n(n+1)2【答案】C【知识点】用表格表示变量间的关系;用关系式表示变量间的关系【解析】【解答】解:∵物体总个数随着层数的变化而变化,∴A选项说法正确,不符合题意,根据表中数字的变化规律可知y= n(n+1)2,当n=7时,y=28,∴B选项说法正确,不符合题意,根据表中数字的变化规律可知总数增加的越来越快,∴C选项说法错误,符合题意,根据表中数字的变化规律可知y= n(n+1)2,∴D选项说法正确,不符合题意.故答案为:C. 【分析】由表格可得:物体总个数随着层数的变化而变化,据此判断A;根据表格中的数据可得y与n的关系式,令n=7,求出y的值,据此判断B、D;根据表格中的数据变化可判断C.5.(2023八上·江北期末)在同一直角坐标系内作一次函数y1=ax+b和y2=−bx+a图象,可能是( )A. B.C. D.【答案】D【知识点】一次函数图象、性质与系数的关系【解析】【解答】解:A、y1反映a>0,b>0,y2反映a>0,−b>0,则b<0,故本选项错误; B、y1反映a<0,b>0,y2反映a>0,−b>0,则b<0,故本选项错误;C、y1反映a<0,b<0,y2反映a>0,−b<0,则b>0,故本选项错误;D、y1反映a<0,b<0,y2反映a<0,−b>0,则b<0,故本选项错误;故答案为:D. 【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限.6.(2022八上·西安期中)已知函数y=(m−3)x+2是y关于x的一次函数,则m的取值范围是( )A.m≠0 B.m≠3 C.m≠−3 D.m为任意实数【答案】B【知识点】一次函数的定义【解析】【解答】解:y=(m−3)x+2是y关于x的一次函数,∴m−3≠0,即m≠3;故答案为:B. 【分析】形如y=kx+b(k≠0)的函数叫做一次函数,据此解答即可.7.(2021八上·房山期中)小凡遇到了这样一道题目:选择适当的x值,并求x+1x代数式的值.他将同学们的答案进行了如下整理,并有3个大胆的猜测:①当x>0时,代数式x+1x的值随着x的增大而越来越小;②代数式x+1x的值有可能等于1;③当x<0时,代数式x+1x的值随着x的减小而越来越接近于1.推测正确的有( )A.0个 B.1个 C.2个 D.3个【答案】C【知识点】用表格表示变量间的关系【解析】【解答】解:①x+1x=1+1x,当x>0时,1x的值随着x的增大而越来越小,∴当x>0时,代数式x+1x的值随着x的增大而越来越小,故该项符合题意;②代数式x+1x的值随着x的增大越来越接近1,但不可能等于1,故该项不符合题意;③x+1x=1+1x,当x<0时,代数式x+1x的值随着x的减小而越来越接近于1,故该项符合题意;故答案为:C.【分析】结合表格中的数据逐项判断即可。8.(2023八上·金东期末)A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;②甲出发4h后被乙追上;③甲比乙晚到53h;④甲车行驶8h或914h,甲,乙两车相距80km;其中错误的( )A.序号① B.序号② C.序号③ D.序号④【答案】D【知识点】通过函数图象获取信息并解决问题;用图象表示变量间的关系【解析】【解答】解:①由图可得,甲车行驶的速度是60÷1=60km/h, 根据图象可知:甲先出发1h,甲出发4h后被乙追上,∴3(v乙−60)=60,∴v乙=80km/h,即乙车行驶的速度是80km/h,故①②正确;③由图可得,当乙到达B地时,甲乙相距100km,∴甲比乙晚到100÷60=53h,故③正确;④由图可得,当乙车在甲车前,且未到达B地时,则60t+80=80(t−1)解得t=8;当乙车到达B地后时,60t+80=80×(9−1),解得t=913,∴甲车行驶8h或913h,甲,乙两车相距80km,故④错误;故答案为:D. 【分析】由图象可得:甲1h行驶的路程为60km,根据路程÷时间=速度可得甲车的速度,然后根据3小时的路程差=60可求出乙车的速度,据此判断①②;由图可得:当乙到达B地时,甲乙相距100km,利用路程÷甲车的速度求出时间,据此判断③;由图可得:当乙车在甲车前,且未到达B地时,60t+80=80(t-1);当乙车到达B地后时,60t+80=80×(9-1),求出t的值,进而判断④.9.(2023八上·长兴期末)如图,在平面直角坐标系中,直线y=43x+4与x轴交于点A,与y轴交于点B,直线y=−4x+4与x轴交于点C,与y轴交于点B,若线段BC上的点D到直线AB的距离DE长为3,则点D的坐标为( )A.(1516,14) B.(3132,18) C.(34,1) D.(56,23)【答案】A【知识点】勾股定理;一次函数图象与坐标轴交点问题【解析】【解答】解:连接AD,把x=0代入y=43x+4得:y=4,∴点B的坐标为(0,4),把y=0代入y=43x+4得:0=43x+4,∴点A的坐标为(−3,0),把y=0代入y=−4x+4得:0=−4x+4,∴点C的坐标为(1,0),∴AB=OA2+OB2=5,AC=1−(−3)=4,∴S△ABC=12×4×4=8,设点D的坐标为(m,−4m+4),则:S△ABC=S△ABD+S△ADC=12×5×3+12×4×(−4m+4)=8,解得:m=1516,−4×1516+4=14,∴点D的坐标为(1516,14),故A正确.故答案为:A.【分析】连接AD,易得A、B、C的坐标,求出AB、AC的值,根据三角形的面积公式可得S△ABC,设D(m,-4m+4),根据S△ABC=S△ABD+S△ADC结合三角形的面积公式可求出m的值,进而可得点D的坐标.10.(2021八上·宝安期末)如图,直线y=−43x+4与x轴交于点B,与y轴交于点C,点E(1,0),D为线段BC的中点,P为y轴上的一个动点,连接PD、PE,当△PED的周长最小时,点P的坐标为( )A.(0,45) B.(0,1) C.(1,0) D.(0,32)【答案】A【知识点】轴对称的应用-最短距离问题;一次函数图象与坐标轴交点问题;一次函数-动态几何问题【解析】【解答】解:如图,作点E关于y轴的对称点F,连接DF,交y轴于点Q,则QE=QF,连接PF,∵△PED的周长=PD+PE+DE=PD+PF+DE≥DF+DE,点D,E是定点,则DE的长不变,∴当PQ重合时,△PED的周长最小,由y=−43x+4,令x=0,y=4,令y=0,则x=3∴B(3,0),C(0,4)∵D是BC的中点∴D(32,2)∵E(1,0),点F是E关于y轴对称的点∴F(−1,0)设直线DF的解析式为:y=kx+b,将D(32,2),F(−1,0)代入,0=−k+b2=32k+b解得k=45b=45∴直线DF的解析式为:y=45x+45令x=0,则y=45即P(0,45)故答案为:A 【分析】利用一次函数图象上点的坐标特征可求出点B、C的坐标,结合点D为线段BC的中点,可求出点D的坐标,作点E关于y轴的对称点F,连接DF,交y轴于点Q,则QE=QF,连接PF,点D,E是定点,则DE的长不变,利用待定系数法可求出直线DF的解析式,利用一次函数图象上点的坐标特征,即可求出点P的坐标。二、填空题(每题4分,共24分)11.(2022八上·黄浦期中)等腰三角形的周长是10厘米,腰长是x厘米,底边长是y厘米,请写出y关于x的函数关系式,并写出自变量x的取值范围 . 【答案】y=−2x+10(5210−2x10−2x>0 ,解得: 520,
∴1003≤x<100,
∴y关于x的函数关系式为y=50x+15000(1003≤x<100);
②依题意得:y=(200-a)x+150(100-x)=(50-a)x+15000(1003≤x≤50),
当100,y随x的增加而增加,
∴当x=34时,y有最小值,最小值为y=(50-a)×34+15000=16700-34a;
∴当正整数a=49时,最小值为y=16700-34×49=15304;
当a=50时,y的值为15000;
当500, 过点N作NM⊥OB于M, ∴∠NMB=∠AOB=90°, ∵∠1+∠3=90°, ∵BN⊥AB, ∴∠ABN=90°, ∴∠1+∠2=90°, ∴∠2=∠3, 又∵BN=BA,∠NMB=∠AOB=90°, ∴△BMN≌△AOB. ∴MN=OB=6, ∴S△OBN=12×OB⋅MN=12×6×6=18, ∴k变化时,△OBN的面积是定值,S△OBN=18;
(3)点Q的坐标为(103,−113)或(8,−6)
【知识点】三角形的面积;一次函数图象与坐标轴交点问题;一次函数-动态几何问题
【解析】【解答】解:(1)①若k=−34,则直线y=kx+6(k≠0)为直线y=−34x+6,
当x=0时,y=6,
∴B(0,6),
当y=0时,x=8,
∴A(8,0),
∴OA=8,OB=6,
故答案为:8,6;
②作ED⊥OB于D,
∴∠BDE=∠AOB=90°,
∴∠2+∠3=90°,
又∵△ABE是以B为直角顶点的等腰直角三角形,
∴AB=BE,∠ABE=90°,
∴∠1+∠2=90°,
∴∠1=∠3,
∴△BED≌△ABO,
∴DE=OB=6,BD=OA=8,
∴OD=OB+BD=14,
∴点E的坐标为(6,14);
(3)当n<10时,过点P作PS⊥x轴于S,过点Q作QT⊥PS于T,
∴∠CSP=∠PTQ=90°,
∵∠2+∠3=90°,
∵∠CPQ=90°,
∴∠1+∠2=90°,
∴∠1=∠3,
又∵PC=PQ,∠CAP=∠PTQ=90°,
∴△PCS≌△QPT.
∴QT=PS=4,PT=SC=10−n,
∴ST=14−n,
∴点Q的坐标为(4+n,n−14),
∵k=−32,
∴直线y=−32x+6,
将点Q的坐标代入y=−32x+6得,n−14=−32(4+n)+6,
解得: n=285,
∴4+n=485,n−14=−425
∴点Q的坐标为(485,−425);
当n>10时,过点P作PS⊥x轴于S,过点Q作QT⊥PS于T,
∴∠CSP=∠PTQ=90°,
∵∠1+∠3=90°,
∵∠CPQ=90°,
∴∠1+∠2=90°,
∴∠2=∠3,
又∵PC=PQ,∠CAP=∠PTQ=90°,
∴△PCS≌△QPT(AAS).
∴QT=PS=4,PT=SC=n−10,
∴ST=n−6,
∴点Q的坐标为(n−4,6−n),
∵k=−32,
∴直线y=−32x+6,
将点Q的坐标代入y=−32x+6得,6−n=−32(n−4)+6,
解得:n=12,
∴点Q的坐标为(8,−6).
综上,点Q的坐标为(103,−113)或(8,−6).
【分析】(1)①将x=0和y=0分别代入y=kx+6(k≠0)求出点A、B的坐标,即可得到OA和OB的长;
②作ED⊥OB于D,先证明△BED≌△ABO,可得DE=OB=6,BD=OA=8,利用线段的和差求出OD的长,即可得到点E的坐标;
(2) 过点N作NM⊥OB于M, 先证明△BMN≌△AOB,可得MN=OB=6,利用三角形的面积公式求出S△OBN=12×OB⋅MN=12×6×6=18,即可得到S△OBN=18;
(3)分类讨论:①当n<10时,过点P作PS⊥x轴于S,过点Q作QT⊥PS于T,②当n>10时,过点P作PS⊥x轴于S,过点Q作QT⊥PS于T,再利用全等三角形的判定方法和性质求解即可。
x01234…y88.599.510… x 1 2 3 4 5 y 6 7 8 9 1 x 1 2 3 4 5 y 8 8 8 8 10 x 1 2 2 4 5 y 6 3 2 1 5 x 1 2 3 4 5 y 2 4 6 8 10 层数n/层12345……物体总数y/个1361015……x12345…x+1x232435465…
2023年浙教版数学八年级上册第五章 一次函数 单元测试(B卷)一、选择题(每题3分,共30分)1.弹簧挂重物会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)有下面的关系. 下列说法不正确的是( )A.x与y都是变量,x是自变量,y是因变量B.所挂物体为6kg,弹簧长度为11cmC.物体每增加1kg,弹簧长度就增加0.5cmD.挂30kg物体时一定比原长增加15cm【答案】D【知识点】常量、变量【解析】【解答】解:由表格可得到,x与y都是变量,x是自变量,y是因变量;物体每增加1kg,弹簧长度就增加0.5cm;所挂物体为6kg,弹簧长度为8+0.5×6=11cm;挂30kg物体时长为8+15>20,不符合已知条件。故选项D错误。 故答案为:D。 【分析】由表格可知:所挂物体每增加1kg,弹簧就伸长0.5cm,据此逐个判断即可。2.(2020八上·烈山期中)下列各列表中,不能表示y是x的函数的是( ) A. B.C. D.【答案】C【知识点】函数的概念【解析】【解答】解:A、B、D对于每个x,都有唯一的y值与之对应,故y是x的函数;C中x=2时,有2个不同的函数值,故y不是x的函数;故答案为:C.【分析】根据函数的定义对选项一一判断即可。3.(2023八上·宁波期末)在直角三角形ABC中,∠C=90∘,∠A=x,∠B=2y,则y与x之间的函数关系式是( )A. B.C. D.【答案】A【知识点】用图象表示变量间的关系【解析】【解答】解:∵在Rt△ABC中,∠C=90°,∠A=x,∠B=2y, ∴∠A+∠B=90°,即x+2y=90°, ∴y=-12x+45° 当x=0°时,y=45°, 当y=0时,x=90°, ∴函数y=-12x+45°与x轴和y轴的交点坐标分别为(90°,0),(0,45°). 故答案为:A. 【分析】根据直角三角形两锐角互余可得∠A+∠B=90°,即可表示出函数关系式为y=-12x+45°,进而求出其与x轴和y轴的交点坐标,即可判断得出结论.4.瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )A.在这个变化过程中层数是自变量,物体总数是因变量B.当堆放层数为7层时,物体总数为28个C.物体的总数随着层数的增加而均匀增加D.物体的总数y与层数n之间的关系式为y=n(n+1)2【答案】C【知识点】用表格表示变量间的关系;用关系式表示变量间的关系【解析】【解答】解:∵物体总个数随着层数的变化而变化,∴A选项说法正确,不符合题意,根据表中数字的变化规律可知y= n(n+1)2,当n=7时,y=28,∴B选项说法正确,不符合题意,根据表中数字的变化规律可知总数增加的越来越快,∴C选项说法错误,符合题意,根据表中数字的变化规律可知y= n(n+1)2,∴D选项说法正确,不符合题意.故答案为:C. 【分析】由表格可得:物体总个数随着层数的变化而变化,据此判断A;根据表格中的数据可得y与n的关系式,令n=7,求出y的值,据此判断B、D;根据表格中的数据变化可判断C.5.(2023八上·江北期末)在同一直角坐标系内作一次函数y1=ax+b和y2=−bx+a图象,可能是( )A. B.C. D.【答案】D【知识点】一次函数图象、性质与系数的关系【解析】【解答】解:A、y1反映a>0,b>0,y2反映a>0,−b>0,则b<0,故本选项错误; B、y1反映a<0,b>0,y2反映a>0,−b>0,则b<0,故本选项错误;C、y1反映a<0,b<0,y2反映a>0,−b<0,则b>0,故本选项错误;D、y1反映a<0,b<0,y2反映a<0,−b>0,则b<0,故本选项错误;故答案为:D. 【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限.6.(2022八上·西安期中)已知函数y=(m−3)x+2是y关于x的一次函数,则m的取值范围是( )A.m≠0 B.m≠3 C.m≠−3 D.m为任意实数【答案】B【知识点】一次函数的定义【解析】【解答】解:y=(m−3)x+2是y关于x的一次函数,∴m−3≠0,即m≠3;故答案为:B. 【分析】形如y=kx+b(k≠0)的函数叫做一次函数,据此解答即可.7.(2021八上·房山期中)小凡遇到了这样一道题目:选择适当的x值,并求x+1x代数式的值.他将同学们的答案进行了如下整理,并有3个大胆的猜测:①当x>0时,代数式x+1x的值随着x的增大而越来越小;②代数式x+1x的值有可能等于1;③当x<0时,代数式x+1x的值随着x的减小而越来越接近于1.推测正确的有( )A.0个 B.1个 C.2个 D.3个【答案】C【知识点】用表格表示变量间的关系【解析】【解答】解:①x+1x=1+1x,当x>0时,1x的值随着x的增大而越来越小,∴当x>0时,代数式x+1x的值随着x的增大而越来越小,故该项符合题意;②代数式x+1x的值随着x的增大越来越接近1,但不可能等于1,故该项不符合题意;③x+1x=1+1x,当x<0时,代数式x+1x的值随着x的减小而越来越接近于1,故该项符合题意;故答案为:C.【分析】结合表格中的数据逐项判断即可。8.(2023八上·金东期末)A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;②甲出发4h后被乙追上;③甲比乙晚到53h;④甲车行驶8h或914h,甲,乙两车相距80km;其中错误的( )A.序号① B.序号② C.序号③ D.序号④【答案】D【知识点】通过函数图象获取信息并解决问题;用图象表示变量间的关系【解析】【解答】解:①由图可得,甲车行驶的速度是60÷1=60km/h, 根据图象可知:甲先出发1h,甲出发4h后被乙追上,∴3(v乙−60)=60,∴v乙=80km/h,即乙车行驶的速度是80km/h,故①②正确;③由图可得,当乙到达B地时,甲乙相距100km,∴甲比乙晚到100÷60=53h,故③正确;④由图可得,当乙车在甲车前,且未到达B地时,则60t+80=80(t−1)解得t=8;当乙车到达B地后时,60t+80=80×(9−1),解得t=913,∴甲车行驶8h或913h,甲,乙两车相距80km,故④错误;故答案为:D. 【分析】由图象可得:甲1h行驶的路程为60km,根据路程÷时间=速度可得甲车的速度,然后根据3小时的路程差=60可求出乙车的速度,据此判断①②;由图可得:当乙到达B地时,甲乙相距100km,利用路程÷甲车的速度求出时间,据此判断③;由图可得:当乙车在甲车前,且未到达B地时,60t+80=80(t-1);当乙车到达B地后时,60t+80=80×(9-1),求出t的值,进而判断④.9.(2023八上·长兴期末)如图,在平面直角坐标系中,直线y=43x+4与x轴交于点A,与y轴交于点B,直线y=−4x+4与x轴交于点C,与y轴交于点B,若线段BC上的点D到直线AB的距离DE长为3,则点D的坐标为( )A.(1516,14) B.(3132,18) C.(34,1) D.(56,23)【答案】A【知识点】勾股定理;一次函数图象与坐标轴交点问题【解析】【解答】解:连接AD,把x=0代入y=43x+4得:y=4,∴点B的坐标为(0,4),把y=0代入y=43x+4得:0=43x+4,∴点A的坐标为(−3,0),把y=0代入y=−4x+4得:0=−4x+4,∴点C的坐标为(1,0),∴AB=OA2+OB2=5,AC=1−(−3)=4,∴S△ABC=12×4×4=8,设点D的坐标为(m,−4m+4),则:S△ABC=S△ABD+S△ADC=12×5×3+12×4×(−4m+4)=8,解得:m=1516,−4×1516+4=14,∴点D的坐标为(1516,14),故A正确.故答案为:A.【分析】连接AD,易得A、B、C的坐标,求出AB、AC的值,根据三角形的面积公式可得S△ABC,设D(m,-4m+4),根据S△ABC=S△ABD+S△ADC结合三角形的面积公式可求出m的值,进而可得点D的坐标.10.(2021八上·宝安期末)如图,直线y=−43x+4与x轴交于点B,与y轴交于点C,点E(1,0),D为线段BC的中点,P为y轴上的一个动点,连接PD、PE,当△PED的周长最小时,点P的坐标为( )A.(0,45) B.(0,1) C.(1,0) D.(0,32)【答案】A【知识点】轴对称的应用-最短距离问题;一次函数图象与坐标轴交点问题;一次函数-动态几何问题【解析】【解答】解:如图,作点E关于y轴的对称点F,连接DF,交y轴于点Q,则QE=QF,连接PF,∵△PED的周长=PD+PE+DE=PD+PF+DE≥DF+DE,点D,E是定点,则DE的长不变,∴当PQ重合时,△PED的周长最小,由y=−43x+4,令x=0,y=4,令y=0,则x=3∴B(3,0),C(0,4)∵D是BC的中点∴D(32,2)∵E(1,0),点F是E关于y轴对称的点∴F(−1,0)设直线DF的解析式为:y=kx+b,将D(32,2),F(−1,0)代入,0=−k+b2=32k+b解得k=45b=45∴直线DF的解析式为:y=45x+45令x=0,则y=45即P(0,45)故答案为:A 【分析】利用一次函数图象上点的坐标特征可求出点B、C的坐标,结合点D为线段BC的中点,可求出点D的坐标,作点E关于y轴的对称点F,连接DF,交y轴于点Q,则QE=QF,连接PF,点D,E是定点,则DE的长不变,利用待定系数法可求出直线DF的解析式,利用一次函数图象上点的坐标特征,即可求出点P的坐标。二、填空题(每题4分,共24分)11.(2022八上·黄浦期中)等腰三角形的周长是10厘米,腰长是x厘米,底边长是y厘米,请写出y关于x的函数关系式,并写出自变量x的取值范围 . 【答案】y=−2x+10(52
相关资料
更多









