2023年广西贵港市港北区中考二模数学试题

这是一份2023年广西贵港市港北区中考二模数学试题，共20页。

A．﹣2023B．2023C．D．
2．（3分）下列图形中既是中心对称图形又是轴对称图形的是（ ）
A．B．C．D．
3．（3分）新华网，2023年4月14日，我国首颗太阳探测卫星“夸父一号”已获得原始太阳观测数据大约84000000兆字节．将数据84000000用科学记数法表示为（ ）
A．0.84×108B．8.4×108C．8.4×106D．8.4×107
4．（3分）下列计算正确的是（ ）
A．2a+3b＝5abB．2（2a﹣b）＝4a﹣b
C．（3a）2＝9aD．a6÷a4＝a2
5．（3分）已知点P（m2+1，﹣1）与点Q关于原点对称，则点Q一定在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
6．（3分）如图，将木条a，b与c钉在一起，∠1＝110°，∠2＝50°，要使木条a与b平行，木条a顺时针旋转的度数至少是（ ）
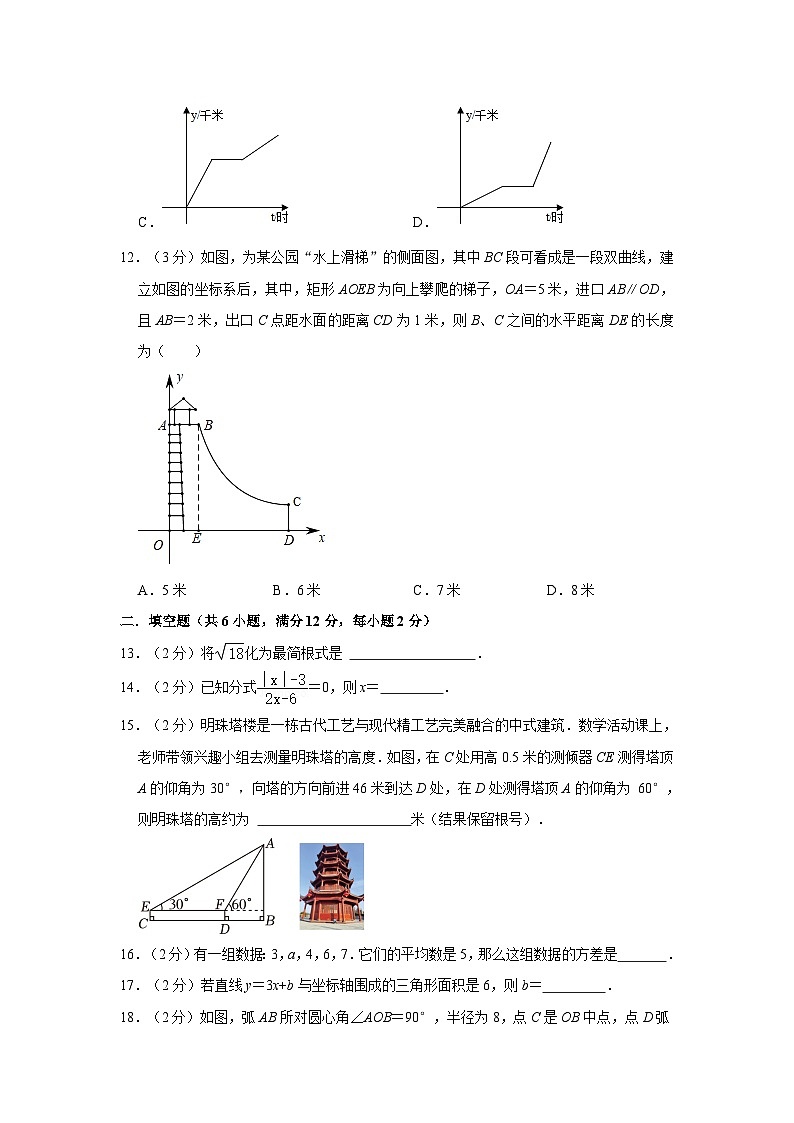
A．10°B．20°C．30°D．40°
7．（3分）若关于x的方程kx2﹣2x﹣1＝0有两个不相等的实数根，则k的取值范围是（ ）
A．k＞﹣1且k≠0B．k＞﹣1C．k＜﹣1D．k＜1且k≠0
8．（3分）下列事件是必然事件的是（ ）
A．三角形内角和等于180°
B．同旁内角互补
C．打开电视正在播新闻
D．乘坐公共汽车恰好有空座
9．（3分）《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：今有甲种袋子中装有黄金9枚（每枚黄金重量相同），乙种袋子中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲种袋子比乙种袋子轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，则可建立方程为（ ）
A．
B．
C．
D．
10．（3分）如图，△ABC是⊙O的内接三角形，AB＝2，∠ACB＝60°，连接OA，OB，则的长是（ ）
A．B．C．πD．
11．（3分）如图，小刚骑电动车到单位上班，最初以某一速度匀速行进，途中由于遇到火车挡道，停下等待放行，耽误了几分钟，为了按时到单位，小刚加快了速度，仍保持匀速行进，结果准时到单位．小刚行进的路程y（千米）与行进时间t（小时）的函数图象的示意图，你认为正确的是（ ）
A．B．
C．D．
12．（3分）如图，为某公园“水上滑梯”的侧面图，其中BC段可看成是一段双曲线，建立如图的坐标系后，其中，矩形AOEB为向上攀爬的梯子，OA＝5米，进口AB∥OD，且AB＝2米，出口C点距水面的距离CD为1米，则B、C之间的水平距离DE的长度为（ ）
A．5米B．6米C．7米D．8米
二．填空题（共6小题，满分12分，每小题2分）
13．（2分）将化为最简根式是 ．
14．（2分）已知分式＝0，则x＝ ．
15．（2分）明珠塔楼是一栋古代工艺与现代精工艺完美融合的中式建筑．数学活动课上，老师带领兴趣小组去测量明珠塔的高度．如图，在C处用高0.5米的测倾器CE测得塔顶A的仰角为30°，向塔的方向前进46米到达D处，在D处测得塔顶A的仰角为 60°，则明珠塔的高约为 米（结果保留根号）．
16．（2分）有一组数据：3，a，4，6，7．它们的平均数是5，那么这组数据的方差是 ．
17．（2分）若直线y＝3x+b与坐标轴围成的三角形面积是6，则b＝ ．
18．（2分）如图，弧AB所对圆心角∠AOB＝90°，半径为8，点C是OB中点，点D弧AB上一点，CD绕点C逆时针旋转90°得到CE，则AE的最小值是 ．
三．解答题（共8小题，满分72分）
19．（6分）计算：．
20．（6分）先化简，再求值：，其中x＝﹣2．
21．（10分）尺规作图（只保留作图痕迹，不要求写出作法）．
如图，已知∠α和线段a，求作等腰△ABC，使∠B＝∠α，底边BC＝a．
22．（10分）如图已知点A（4，a）、B（﹣10，﹣4）是一次函数y＝kx+b图象与反比例函数y＝图象的交点，且一次函数与x轴交于C点．
（1）求该反比例函数和一次函数的解析式；
（2）连接AO，求△AOB的面积；
（3）在y轴上有一点P，使得S△AOP＝S△AOC，求出点P的坐标．
23．（10分）2022年是我国航天事业辉煌的一年，神舟十四号和神舟十五号两个飞行乘组6位航天员在太空会师，在神州大地上掀起了航天热潮，某学校为了解本校学生对我国航天事业的了解情况，在全校范围内开展了航天知识竞赛，学校随机抽取了50名学生的成绩，整理并制成了如下不完整的频数分布表和频数分布直方图．
其中60≤x＜70这一组的数据如下：
61，62，62，63，64，64，64，64，64，64，64，64，64，64，66，67，67，69
根据以上提供的信息，解答下列问题：
（1）表格中a＝ ，b＝ ，m＝ ；
（2）60≤x＜70这一组数据的众数是 ，中位数是 ；
（3）若以组中值（每组正中间数值）为本组数据的平均数，全校共有1500名学生参与竞赛，试估计所有学生成绩的平均分．
24．（10分）为实现“乡村振兴”战略目标，某乡镇制定了“以产业带动发展”的策略，开发出了某新型农产品，计划租用A，B两种型号的货车将该农产品运往外地销售，已知用1辆A型车和2辆B型车载满该农产品一次可运11吨；用2辆A型车和1辆B型车载满该农产品一次可运10吨．现有该农产品31吨，计划一次运完，且每辆车都满载．
（1）1辆A型货车和1辆B型货车满载时一次分别运该农产品多少吨？
（2）若1辆A型货车需租金100元/次，1辆B型货车需租金120元/次，请问有几种租车方案？哪种最省钱？
25．（10分）综合与实践
【问题情境】数学活动课上，老师准备了若干张正方形纸片ABCD，组织同学们进行折纸探究活动．
【初步尝试】把正方形对折，折痕为EF，然后展开，沿过点A与点E所在的直线折叠，点B落在点B'处，连接 B'C，如图1，请直接写出∠AEB'与∠ECB'的数量关系．
【能力提升】把正方形对折，折痕为EF，然后展开，沿过点A与BE上的点G所在的直线折叠，使点B落在EF上的点P处，连接PD，如图2，猜想∠APD的度数，并说明理由．
【拓展延伸】在图2的条件下，作点A关于直线CP的对称点A'，连接PA′，BA′，AC，如图3，求∠PA′B的度数．
26．（10分）如图，在平面直角坐标系中，二次函数y＝﹣x2+bx﹣c的图象与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C．
（1）求这个二次函数的表达式．
（2）如图1，二次函数图象的对称轴与直线AC：y＝x+3交于点D，若点M是直线AC上方抛物线上的一个动点，求△MCD面积的最大值．
（3）如图2，点P是直线AC上的一个动点，过点P的直线l与BC平行，则在直线l上是否存在点Q，使点B与点P关于直线CQ对称？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
参考答案与试题解析
一．选择题（共12小题，满分36分，每小题3分）
1． 解：﹣（﹣2023）＝2023，
故选：B．
2． 解：A、是轴对称图形，不是中心对称图形，故本选项不合题意；
B、既是轴对称图形，又是中心对称图形，故本选项符合题意；
C、是轴对称图形，不是中心对称图形，故本选项不合题意；
D、是轴对称图形，不是中心对称图形，故本选项不合题意．
故选：B．
3． 解：84000000＝8.4×107．
故选：D．
4． 解：A.2a与3b不是同类项，所以不能合并，故本选项不合题意；
B.2（2a﹣b）＝4a﹣2b，故本选项不合题意；
C．（3a）2＝9a2，故本选项不合题意；
D．a6÷a4＝a2，故本选项符合题意．
故选：D．
5． 解：∵点P（m2+1，﹣1）与点Q关于原点对称，
∴Q（﹣m2﹣1，1），
∵﹣m2﹣1＜0，1＞0，
∴点Q一定在第二象限，
故选：B．
6． 解：当直线a顺时针旋转到a'位置时，直线a∥b，则a'∥b，
∵∠2＝50°，
∴∠3＝∠2＝50°，
∵∠1＝110°，
∴旋转的角度为180°﹣∠1﹣∠3＝180°﹣110°﹣50°＝20°，
故选：B．
7． 解：根据题意得k≠0且Δ＝（﹣2）2﹣4×k×（﹣1）＞0，
所以k＞﹣1且k≠0．
故选：A．
8． 解：A．三角形内角和等于180°是必然事件，此选项符合题意；
B．同旁内角互补是随机事件，此选项不符合题意；
C．打开电视正在播新闻是随机事件，此选项不符合题意；
D．乘坐公共汽车恰好有空座是随机事件，此选项不符合题意；
故选：A．
9． 解：设每枚黄金重x两，每枚白银重y两，
依题意，得：．
故选：C．
10． 解：过点O作OD⊥AB于D，
则AD＝DB＝AB＝，
由圆周角定理得：∠AOB＝2∠ACB＝120°，
∴∠AOD＝60°，
∴OA＝＝＝2，
∴的长＝＝，
故选：D．
11． 解：随着时间的增多，行进的路程也将增多，排除A；
由于途中由于遇到火车挡道，停下等待放行，耽误了几分钟，此时时间在增多，而路程没有变化，排除B；
后来加快了速度，仍保持匀速行进，所以后来的函数图象的走势应比前面匀速前进的走势要陡．
故选：D．
12． 解：∵四边形AOEB是矩形，
∴BE＝OA＝5，AB＝2，
∴B（2，5），
设双曲线BC的解析式为y＝，
∴k＝10，
∴y＝，
∵CD为1
∴当y＝1时，x＝10，
∴DE的长＝10﹣2＝8m，
故选：D．
二．填空题（共6小题，满分12分，每小题2分）
13． 解：＝＝3，
故答案为：3．
14． 解：由题意得：，
解①得：x＝±3，
解②得x≠3，
∴x＝﹣3，
故答案为﹣3．
15． 解：如图，
设AG＝x米，
在Rt△AFG中，∠AFG＝60°，tan∠AFG＝＝，
∴FG＝x，
在Rt△AEG中，∠AEG＝30°，tan∠AEG＝，
∴EG＝x，
∴x﹣x＝46，
解得：x＝23．
∴AG＝23米，
则AB＝（23+0.5）米．
答：明珠塔的高AB为（23+0.5）米．
故答案为：（23+0.5）．
16． 解：a＝5×5﹣3﹣4﹣6﹣7＝5，
s2＝[（3﹣5）2+（5﹣5）2+（4﹣5）2+（6﹣5）2+（7﹣5）2]＝2．
故答案为：2．
17． 解：∵直线y＝3x+b与坐标轴围成的三角形面积是6，
∴b≠0．
①当b＞0时，y＝3x+b的图象如图1．
当x＝0时，y＝3×0+b＝b，则B（0，b），此时OB＝b．
当y＝0时，3x+b＝0，故x＝，则A（，0），此时OA＝．
∴＝6．
∴b＝6或b＝﹣6（不合题意，故舍去）．
②当b＜0时，y＝3x+b的图象如图2．
当x＝0时，y＝3×0+b＝b，则B（0，b），此时OB＝﹣b．
当y＝0时，3x+b＝0，故x＝，则A（，0），此时OA＝﹣．
∴＝6．
∴b＝6（不合题意，故舍去）或b＝﹣6．
综上：b＝±6．
故答案为：±6．
18． 解：如图，连OD，以OC为边向下作正方形OCTH，连AT，ET．
∵OA＝OB＝8，OC＝CB＝CT＝OH＝HT＝4，
∴AH＝AO+OH＝12，
∴AT＝＝＝4，
∴∠OCT＝∠ECD＝90°，
∴∠OCD＝∠RCE，
在△OCD和△TCE中，
，
∴△OCD≌△TCE（SAS），
∴ET＝OD＝8，
∴AE≥AT﹣ET＝4﹣8，
∴AE的最小值为 4﹣8．
故答案为：4﹣8．
三．解答题（共8小题，满分72分）
19． 解：
＝﹣3+2+﹣1﹣4×
＝﹣2+﹣2
＝﹣2﹣．
20． 解：
＝
＝•
＝，
当时，
原式＝．
21． 解：如图，△ABC即为所求．
22． 解：（1）∵点A（4，a）、B（﹣10，﹣4）是一次函数y＝kx+b图象与反比例函数y＝图象的交点，
∴﹣4＝，
∴m＝40，
∴反比例函数为y＝，
把A（4，a）代入得，a＝＝10，
∴A（4，10），
把A（4，10），B（﹣10，﹣4）代入y＝kx+b得，
解得，
∴一次函数的解析式为y＝x+6；
（2）在y＝x+6中，令y＝0，求得x＝﹣6，
∴C（﹣6，0），
∴S△AOB＝S△AOC+S△BOC＝＝42；
（3）∵S△AOC＝＝30，S△AOP＝S△AOC，
∴OP•xA＝30，即OP×4＝30，
∴OP＝15，
∴P（0，15）或（0，﹣15）．
23． 解：（1）a＝50×0.1＝5，b＝50﹣（2+5+18+9+2）＝14，
∴m＝14÷50＝0.28，
故答案为：5，14，0.28；
（2）根据60≤x＜70这一组的数据：61，62，64，64，64，64，64，64，64，64，64，64，64，64，64，64，64，69，可知众数为64；
中位数是：＝64，
故答案为：64，64；
（3）×（45×2+55×5+65×18+75×9+85×14+95×2）＝71.8（分），
答：估计所有学生成绩的平均分约为71.8分．
24． 解：（1）设1辆A型货车载满该农产品一次可运送x吨，1辆B型货车载满该农产品一次可运送y吨，
由题意可得：，
解得：，
答：1辆A型货车载满该农产品一次可运送3吨，1辆B型货车载满该农产品一次可运送4吨；
（2）设租用A型货车α辆，B型货车b辆，
由题意可得：3a+4b＝31，
∴a＝，
又∵a，b均为非负整数，
∴或或，
∴该物流公司共有3种租车方案，
方案1：租用9辆A型车，1辆B型车；
方案2：租用5辆A型车，4辆B型车；
方案3：租用1辆A型车，7辆B型车，
∴方案1的费用：9×100+1×120＝1020元，
方案2的费用：5×100+4×120＝980元，
方案1的费用：1×100+7×120＝940元，
∵1020＞980＞940，
∴方案3最省钱．
25． 解：（1）∠AEB'＝∠ECB'．
连接BB'，
∵把正方形对折，
∴E为BC的中点，
∴BE＝CE，
∵沿过点A与点E所在的直线折叠，点B落在点B'处，
∴BE＝BE'，∠AEB＝∠AEB'，BB'⊥AE，
∴BE＝CE＝BE'
∴∠BB'C＝90°，
∴AE∥CB'，
∴∠AEB＝∠ECB'，
∴∠AEB'＝∠ECB'；
（2）猜想：∠APD＝60°．
理由：∵四边形ABCD是正方形，
∴AB＝BC＝CD＝DA，∠ADC＝90°，
由折叠性质可得：，EF⊥AD．
∴PA＝PD＝AD，
∴△APD是等边三角形，
∴∠APD＝60°；
（3）解：连接A'C、AA'，
由（2）得△APD是等边三角形，
∴∠PAD＝∠PDA＝∠APD＝60°，AP＝DP＝AD，
∵∠ADC＝90°，
∴∠PDC＝30°，
又∵PD＝AD＝DC，
∴∠DPC＝∠DCP＝，∠DAC＝∠DCA＝45°，
∴∠PAC＝∠PAD﹣∠DAC＝60°﹣45°＝15°，∠ACP＝∠DCP﹣∠DCA＝75°﹣45°＝30°．
由对称性质得：AC＝A'C，∠ACP＝∠A'CP＝30°，
∴∠ACA'＝60°，
∴△ACA'是等边三角形，
在△AA'B 与△CA'B中，
，
∴△AA'B≌△CA'B（SSS），
∴∠AA'B＝∠CA'B＝∠AA'C＝30°，
又∵∠CA'P＝∠CAP＝15°，
∴∠PA'B＝∠CA'B﹣∠CA'P＝15°．
26． 解：（1）由题意得，
y＝﹣（x+3）（x﹣1）＝﹣x2﹣2x+3；
（2）如图1，
作MQ⊥AC于Q，作ME⊥AB于F，交AC于E，
∵OA＝OC＝3，∠AOC＝90°，
∴∠CAO＝∠ACO＝45°，
∴∠MEQ＝∠AEF＝90°﹣∠CAO＝45°，
抛物线的对称轴是直线：x＝，
∴y＝x+3＝﹣1+3＝2，
∴D（1，2），
∵C（0，3），
∴CD＝，
故只需△MCD的边CD上的高最大时，△MCD的面积最大，
设过点M与AC平行的直线的解析式为：y＝x+m，
当直线y＝x+m与抛物线相切时，△MCD的面积最大，
由x+m＝﹣x2﹣2x+3得，
x2+3x+（m﹣3）＝0，
由Δ＝0得，
32﹣4（m﹣3）＝0得，
m﹣3＝，
∴x2+3x+＝0，
∴x1＝x2＝﹣，
∴y＝﹣（﹣）2﹣2×+3＝，
y＝x+3＝﹣+3＝，
∴ME＝，
∴MQ＝ME•sin∠MEQ＝ME•sin45°＝，
∴S△MCD最大＝＝；
（3）如图2，
当点P在线段AC上时，连接BP，交CQ于R，
∵点B和点Q关于CQ对称，
∴CP＝CB，
设P（t，t+3），
由CP2＝CB2得，
2t2＝10，
∴t1＝﹣，t2＝（舍去），
∴P（﹣，3﹣），
∵PQ∥BC，
∴，
∴CR＝QR，
∴四边形BCPQ是平行四边形，
∵1+（﹣）﹣0＝1﹣，0+（3﹣）﹣3＝﹣，
∴Q（1﹣，﹣）；
如图3，
当点P在AC的延长线上时，由上可知：P（，3+），
同理可得：Q（1+，），
综上所述：Q（1﹣，﹣）或（1+，）
组号
成绩
频数
频率
1
140≤x＜50
2
0.04
2
50≤x＜60
a
0.1
3
60≤x＜70
18
0.36
4
70≤x＜80
9
0.18
5
80≤x＜90
b
m
6
90≤x≤100
2
0.05
合计
50
1.000