2023-2024学年福建省龙岩市长汀县七年级（上）期中数学试卷（含解析）

这是一份2023-2024学年福建省龙岩市长汀县七年级（上）期中数学试卷（含解析），共17页。试卷主要包含了选择题，填空，解答题等内容，欢迎下载使用。

1．已知一个数的相反数为3，则这个数为（ ）
A．3B．C．﹣3D．﹣
2．某潜水艇停在海面下500米处，先下降200米，又上升130米，这时潜水艇停在海面下多少米处（ ）
A．430B．530C．570D．470
3．下列运算中，正确的是（ ）
A．3a+5b＝8abB．3y2﹣y2＝3
C．6a3+4a3＝10a6D．5m2n﹣3nm2＝2m2n
4．已知2022xny与2023x3ym是同类项，则（m﹣n）2的值为（ ）
A．8B．﹣8C．16D．4
5．化简|﹣2|，﹣（﹣2）2，﹣（﹣2），（﹣2）3这四个数中，负数的个数有（ ）
A．1个B．2个C．3个D．4个
6．某商品的价格m元，涨价10%后，9折优惠，该产品售价为（ ）
A．90%m元B．99%m元C．110%m元D．81%m元
7．小芳和小明在手工课上各自制作楼梯模型，他们用的材料如图，则（ ）
A．一样多B．小明多C．小芳多D．不能确定
8．对有理数a、b，定义运算*如下：a*b＝（a+b）﹣（a﹣b），如：2*5＝（2+5）﹣（2﹣5）＝7﹣（﹣3）＝7+3＝10．试求（﹣3）*4的值．（ ）
A．﹣8B．6C．﹣6D．8
9．代数式2x2+3x+7的值是12，那么代数式6x2+9x﹣7的值（ ）
A．8B．﹣8C．22D．﹣22
10．下列说法正确的是（ ）
A．如果a＞b，那么a2＞b2B．如果a2＞b2，那么a＞b
C．如果|a|＞|b|，那么a2＞b2D．如果a＞b，那么|a|＞|b|
二、填空。（本大题共6题，每题4分，共24分）
11．是 次单项式．
12．比较大小：﹣3.3 ﹣3.4（填“＞”或“＜”或“＝”）．
13．据国家统计局网站2023年6月14日发布消息，2023年福建省粮食总产量约为49950000吨，将49950000用科学记数法表示为 ．
14．珠穆朗玛峰海拔高度：8848米，吐鲁番盆地海拔高度：﹣155米，那么珠峰比吐鲁番盆地高 米．
15．有理数m，n在数轴上的位置如图所示，则下列关系式中正确的有 个．
①m+n＜0；
②n﹣m＞0；
③n＞0；
④m＞0．
16．点A1、A2、A3、…、An（n为正整数）都在数轴上．点A1在原点O的左边，且A1O＝1；点A2在点A1的右边，且A2A1＝2；点A3在点A2的左边，且A3A2＝3；点A4在点A3的右边，且A4A3＝4；…，依照上述规律：点A2023所表示的数是 ．
三、解答题。（本大题共9小题，共86分）
17．在数轴上表示下列五个数﹣3.5，3，，，﹣2，并按从小到大的顺序用“＜”把这些数连接起来．
18．计算．
（1）﹣20+（﹣14）﹣（﹣18）﹣13；
（2）．
19．已知a、b为相反数且不为零，c、d互为倒数，m的绝对值是2；求：的值．
20．小明做一道数学题：“已知两个多项式A，B，A＝……，B＝x2+3x﹣2，计算2A+B的值．”小明误把“2A+B”看成“A+2B”，求得的结果为5x2﹣2x+3，请求出2A+B的正确结果．
21．化简求值：4x2y﹣[6xy﹣2（2xy﹣2）﹣x2y]+1，其中，y＝1．
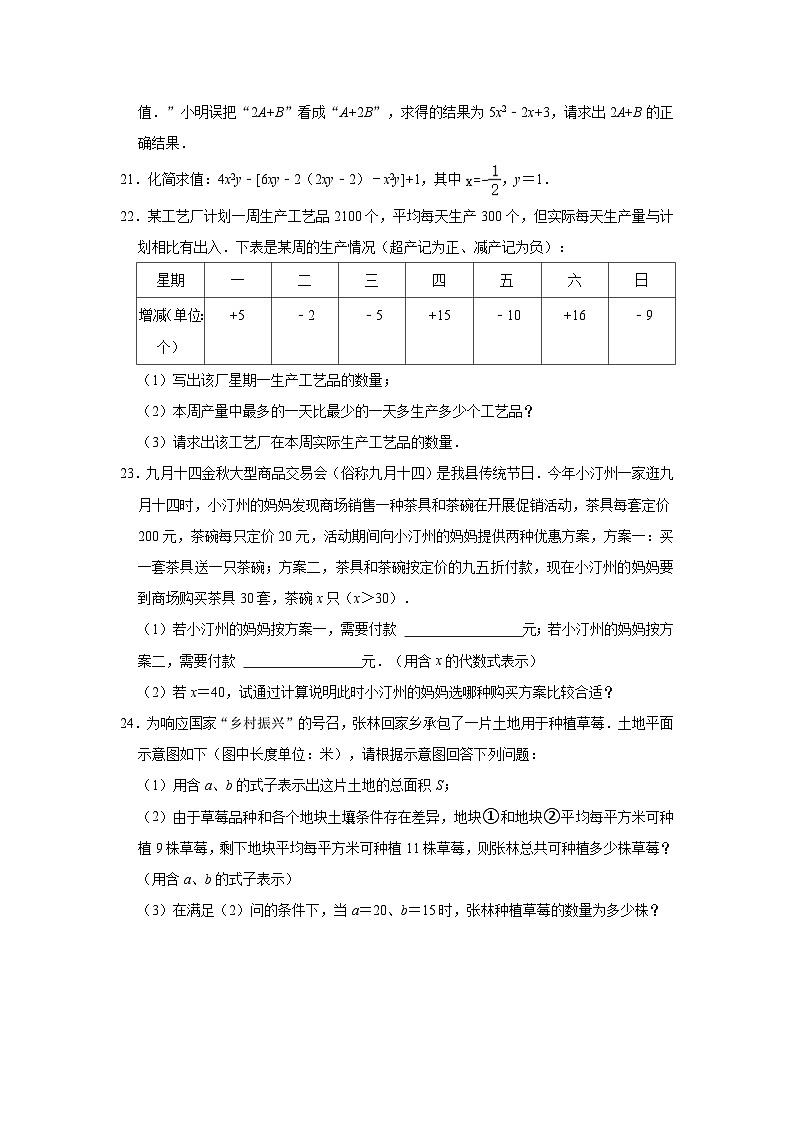
22．某工艺厂计划一周生产工艺品2100个，平均每天生产300个，但实际每天生产量与计划相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：
（1）写出该厂星期一生产工艺品的数量；
（2）本周产量中最多的一天比最少的一天多生产多少个工艺品？
（3）请求出该工艺厂在本周实际生产工艺品的数量．
23．九月十四金秋大型商品交易会（俗称九月十四）是我县传统节日．今年小汀州一家逛九月十四时，小汀州的妈妈发现商场销售一种茶具和茶碗在开展促销活动，茶具每套定价200元，茶碗每只定价20元，活动期间向小汀州的妈妈提供两种优惠方案，方案一：买一套茶具送一只茶碗；方案二，茶具和茶碗按定价的九五折付款，现在小汀州的妈妈要到商场购买茶具30套，茶碗x只（x＞30）．
（1）若小汀州的妈妈按方案一，需要付款 元；若小汀州的妈妈按方案二，需要付款 元．（用含x的代数式表示）
（2）若x＝40，试通过计算说明此时小汀州的妈妈选哪种购买方案比较合适？
24．为响应国家“乡村振兴”的号召，张林回家乡承包了一片土地用于种植草莓．土地平面示意图如下（图中长度单位：米），请根据示意图回答下列问题：
（1）用含a、b的式子表示出这片土地的总面积S；
（2）由于草莓品种和各个地块土壤条件存在差异，地块①和地块②平均每平方米可种植9株草莓，剩下地块平均每平方米可种植11株草莓，则张林总共可种植多少株草莓？（用含a、b的式子表示）
（3）在满足（2）问的条件下，当a＝20、b＝15时，张林种植草莓的数量为多少株？
25．已知|a+1|+（b﹣4）2＝0，c＝2a，且a，b，c分别是点A，B，C在数轴上对应的数．
（1）a，b，c的值分别为a＝ ，b＝ ，c＝ ，并在数轴上标出点A，B，C；
（2）定义：在数轴上，若点D到点E、F的距离之和为6，则点D叫做E和F的“幸福中心”．
①若点G是B和C的“幸福中心”，且点G表示的数是整数，求所有满足条件的点G表示的数之和；
②点Q表示7，点P从点Q出发，以每秒2个单位长度的速度向左运动，同时，点M，N分别从点A，B出发，以每秒1个单位长度的速度向右运动，经过多少秒时，点P是M和N的“幸福中心”？
参考答案
一、选择题。（每小题4分，共40分）
1．已知一个数的相反数为3，则这个数为（ ）
A．3B．C．﹣3D．﹣
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号，求解即可．
解：已知一个数的相反数为3，则这个数为﹣3，
故选：C．
【点评】本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“﹣”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．不要把相反数的意义与倒数的意义混淆．
2．某潜水艇停在海面下500米处，先下降200米，又上升130米，这时潜水艇停在海面下多少米处（ ）
A．430B．530C．570D．470
【分析】下降200米用﹣200米表示，上升130米用+130米表示，根据题意可以列式为：（﹣500）+（﹣200）+130．
解：（﹣500）+（﹣200）+130＝﹣500﹣200+130＝﹣570米，即这时潜水艇停在海面下570米．故选C．
【点评】本题是把实际问题转化为有理数的加减法计算题．
3．下列运算中，正确的是（ ）
A．3a+5b＝8abB．3y2﹣y2＝3
C．6a3+4a3＝10a6D．5m2n﹣3nm2＝2m2n
【分析】根据合并同类项的法则结合选项进行求解，然后选出正确选项．
解：A、3a和5b不是同类项，不能合并，故本选项错误；
B、3y2﹣y2＝2y2，计算错误，故本选项错误；
C、6a3+4a3＝10a3，计算错误，故本选项错误；
D、5m2n﹣3nm2＝2m2n，计算正确，故本选项正确．
故选：D．
【点评】本题考查了合并同类项的知识，解答本题的关键是掌握合并同类项的法则．
4．已知2022xny与2023x3ym是同类项，则（m﹣n）2的值为（ ）
A．8B．﹣8C．16D．4
【分析】根据同类项的概念可求m，n的值，从而求出代数式的值．
解：∵2022xny与2023x3ym是同类项，
∴m＝1，n＝3，
∴（m﹣n）2
＝（1﹣3）2
＝（﹣2）2
＝4，
故选：D．
【点评】此题考查了同类项的概念，解题的关键是掌握同类项定义中的两个“相同”：（1）所含字母相同；（2）相同字母的指数相同．
5．化简|﹣2|，﹣（﹣2）2，﹣（﹣2），（﹣2）3这四个数中，负数的个数有（ ）
A．1个B．2个C．3个D．4个
【分析】首先利用绝对值以及有理数乘方的性质化简各数，进而得出答案．
解：∵|﹣2|＝2，﹣（﹣2）2＝﹣4，﹣（﹣2）＝2，（﹣2）3＝﹣8，
∴这四个数中，负数的个数有2个．
故选：B．
【点评】此题主要考查了正数与负数，正确化简各数是解题关键．
6．某商品的价格m元，涨价10%后，9折优惠，该产品售价为（ ）
A．90%m元B．99%m元C．110%m元D．81%m元
【分析】先求出涨价10%后价格为m（1+10%），9折优惠表示为m（1+10%）×90%，所以该产品售价为99%m元．
解：m（1+10%）×90%＝0.99m．
解得：99%m元．故选B．
【点评】列代数式的关键是正确理解文字语言中的关键词，比如该题中的“涨价10%”、“9折优惠”等，从而明确其中的运算关系，正确地列出代数式．该题要注意的是9折优惠是在涨价10%后m（1+10%）的基础上优惠的．
7．小芳和小明在手工课上各自制作楼梯模型，他们用的材料如图，则（ ）
A．一样多B．小明多C．小芳多D．不能确定
【分析】首先根据已知图形中两个图形中共同含有的边，再判断形状不同的边的长度即可．
解：他们用的铁丝一样长．两个图形右侧边与左侧相等，上侧与下侧相等，
即两个图形都可以利用平移的方法变为长为8cm，宽为5cm的矩形，
所以两个图形的周长都为（8+5）×2＝26cm，
所以他们用的铁丝一样长．
故选：A．
【点评】此题主要考查了平移的应用，考生通过观察、分析识别图形的能力，解决此题的关键是通过观察图形确定右侧与上侧各边的长相等．
8．对有理数a、b，定义运算*如下：a*b＝（a+b）﹣（a﹣b），如：2*5＝（2+5）﹣（2﹣5）＝7﹣（﹣3）＝7+3＝10．试求（﹣3）*4的值．（ ）
A．﹣8B．6C．﹣6D．8
【分析】原式利用题中的新定义计算即可得到结果．
解：根据题中的新定义得：（﹣3）*4＝（﹣3+4）﹣（﹣3﹣4）＝1+7＝8，
故选：D．
【点评】此题考查了有理数的混合运算，弄清题中的新定义是解本题的关键．
9．代数式2x2+3x+7的值是12，那么代数式6x2+9x﹣7的值（ ）
A．8B．﹣8C．22D．﹣22
【分析】根据2x2+3x+7的值为12，可求出2x2+3x＝5，再将6x2+9x﹣7变形为3（2x2+3x）﹣7后整体代入求值即可．
解：∵2x2+3x+7的值是12，
∴2x2+3x+7＝12，
2x2+3x＝5，
∴6x2+9x﹣7
＝3（2x2+3x）﹣7
＝3×5﹣7
＝15﹣7
＝8，
故选：A．
【点评】本题考查代数式求值，正确进行计算是解题关键．
10．下列说法正确的是（ ）
A．如果a＞b，那么a2＞b2B．如果a2＞b2，那么a＞b
C．如果|a|＞|b|，那么a2＞b2D．如果a＞b，那么|a|＞|b|
【分析】比较大小，可以举例子，证明是否正确．
解：若a＝1，b＝﹣3，则a2＜b2，故A错；
若a＝﹣3，b＝1，则a＜b，故B错；
如果|a|＞|b|，那么a2＞b2故C对；
若a＝1，b＝﹣3，则|a|＜|b|，故D错．
故选：C．
【点评】主要考查了平方和绝对值的性质，作为判断正误的题可直接举反例，能举出反例的则不正确．
二、填空。（本大题共6题，每题4分，共24分）
11．是 3 次单项式．
【分析】根据单项式的次数的定义直接解答即可．
解：单项式的次数为：2+1＝3，
故答案为：3．
【点评】本题考查单项式的相关定义：单项式的次数是各字母的指数和．掌握其定义是解题的关键．
12．比较大小：﹣3.3 ＞ ﹣3.4（填“＞”或“＜”或“＝”）．
【分析】根据有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．
解：|﹣3.3|＝3.3，|﹣3.4|＝3.4，3.3＜3.4
∴﹣3.3＞﹣3.4，
故答案为：＞．
【点评】本题考查了有理数的大小比较，解题的关键是掌握有理数的大小比较方法．
13．据国家统计局网站2023年6月14日发布消息，2023年福建省粮食总产量约为49950000吨，将49950000用科学记数法表示为 4.995×107 ．
【分析】已知条件中49950000＞10，49950000整数位数为8，n＝8﹣1＝7，故用科学记数法表示为4.995×107．
解：将49950000用科学记数法表示为4.995×107，
故答案为：4.995×107．
【点评】本题考查了科学记数法表示一个数，一般形式为a×10n，其中1≤|a|＜10，n为整数．确定n的值时，当原数的绝对值≥10时，n为正整数，n等于原数的整数位数减1；当原数的绝对值＜1时，n为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．掌握这个方法是解答本题的关键．
14．珠穆朗玛峰海拔高度：8848米，吐鲁番盆地海拔高度：﹣155米，那么珠峰比吐鲁番盆地高 9003 米．
【分析】用珠峰的高度减去吐鲁番的高度，然后根据减去一个数等于加上这个数的相反数进行计算即可得解．
解：8848﹣（﹣155），
＝8848+155，
＝9003．
故答案为：9003．
【点评】本题考查了有理数的减法，熟记减去一个数等于加上这个数的相反数是解题的关键．
15．有理数m，n在数轴上的位置如图所示，则下列关系式中正确的有 ①④ 个．
①m+n＜0；
②n﹣m＞0；
③n＞0；
④m＞0．
【分析】利用数轴上点位置确定出m，n的符号和它们绝对值的大小，再利用有理数的加减法法则解答即可．
解：由题意得：m＞0，n＜0，|m|＜|n|，
∴m+n＜0，n﹣m＜0．
∴①④正确，②③错误，
∴正确的有①④，
故答案为：①④．
【点评】本题主要考查了有理数的加减法，绝对值的意义，数轴，利用数轴上点位置确定出m，n的符号和它们绝对值的大小是解题的关键．
16．点A1、A2、A3、…、An（n为正整数）都在数轴上．点A1在原点O的左边，且A1O＝1；点A2在点A1的右边，且A2A1＝2；点A3在点A2的左边，且A3A2＝3；点A4在点A3的右边，且A4A3＝4；…，依照上述规律：点A2023所表示的数是 ﹣1012 ．
【分析】分别计算A1，A2，A3，A4所表示的数，得到规律：当奇数个点时是负数，偶数个点时是正数，且奇数点与后面偶数点的数字相同，由A＝1012得到A＝﹣1012．
解：∵点A1在原点O的左边，且A1O＝1，∴点A1表示的数是﹣1，
∵点A2在点A1的右边，且A2A1＝2，∴点A2所表示的数是1，
∵点A3在点A2的左边，且A3A2＝3，∴点A3表示的数是﹣2，
∵点A4在点A3的右边，且A4A3＝4，∴点A4表示的数是2，
⋯，
∴当奇数个点时是负数，偶数个点时是正数，且奇数点与后面偶数点的数字相同，
∴（n为偶数），
∵A＝1012，2023表示的是奇数，
∴A＝﹣1012
故答案为：﹣1012．
【点评】此题考查数字类规律探究，正确理解规律并解决问题是解题的关键．
三、解答题。（本大题共9小题，共86分）
17．在数轴上表示下列五个数﹣3.5，3，，，﹣2，并按从小到大的顺序用“＜”把这些数连接起来．
【分析】先把各数在数轴上表示出来，从左到右用“＜”号连接起来即可．
解：数轴如图所示：
．
【点评】此题考查将数表示在数轴上，利用数轴比较有理数的大小，正确理解数轴上左边的数小于右边的数是解题的关键．
18．计算．
（1）﹣20+（﹣14）﹣（﹣18）﹣13；
（2）．
【分析】（1）原式先去括号，再运用交换律进行负数与负数相加，最后进行加法运算即可；
（2）原式逆用乘法分配律进行计算即可．
解：（1）﹣20+（﹣14）﹣（﹣18）﹣13
＝﹣20﹣14+18﹣13
＝（﹣20﹣14﹣13）+18
＝﹣47+18
＝﹣29；
（2））
＝
＝
＝．
【点评】本题主要考查了有理数的混合运算，熟练掌握运算法则是关键．
19．已知a、b为相反数且不为零，c、d互为倒数，m的绝对值是2；求：的值．
【分析】根据各定义得到，代入计算即可．
解：∵a、b互为相反数，
∴，
∵c、d互为倒数，
∴cd＝1，
∵m的绝对值是2，
∴m＝±2，
当m＝2时，原式＝0+6+1＝7．
当m＝﹣2时，原式＝0﹣6+1＝﹣5．
【点评】此题考查相反数、倒数、绝对值的定义，已知式子的值求代数式的值，熟练掌握各定义得到是解题的关键．
20．小明做一道数学题：“已知两个多项式A，B，A＝……，B＝x2+3x﹣2，计算2A+B的值．”小明误把“2A+B”看成“A+2B”，求得的结果为5x2﹣2x+3，请求出2A+B的正确结果．
【分析】根据整式的运算法则即可求出答案．
解：由题意可知：A+2B＝5x2﹣2x+3，
∴A＝（5x2﹣2x+3）﹣2（x2+3x﹣2）
＝5x2﹣2x+3﹣2x2﹣6x+4
＝3x2﹣8x+7，
∴2A+B
＝2（3x2﹣8x+7）+（x2+3x﹣2）
＝6x2﹣16x+14+x2+3x﹣2
＝7x2﹣13x+12
【点评】本题考查整式的运算法则，解题的关键是熟练运用整式的运算法则，本题属于基础题型．
21．化简求值：4x2y﹣[6xy﹣2（2xy﹣2）﹣x2y]+1，其中，y＝1．
【分析】本题应对代数式进行去括号，合并同类项，将代数式化为最简式，然后把x，y的值代入即可．注意去括号时，如果括号前是负号，那么括号中的每一项都要变号；合并同类项时，只把系数相加减，字母与字母的指数不变．
解：原式＝4x2y﹣[6xy﹣4xy+4﹣x2y]+1
＝4x2y﹣2xy﹣4+x2y+1
＝5x2y﹣2xy﹣3；
当，y＝1时，
原式＝
＝
＝．
【点评】本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．
22．某工艺厂计划一周生产工艺品2100个，平均每天生产300个，但实际每天生产量与计划相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：
（1）写出该厂星期一生产工艺品的数量；
（2）本周产量中最多的一天比最少的一天多生产多少个工艺品？
（3）请求出该工艺厂在本周实际生产工艺品的数量．
【分析】（1）由表格可以求得该厂星期一生产工艺品的数量；
（2）由表格可以求得本周产量中最多的一天比最少的一天多生产多少个工艺品；
（3）由表格可以求得该工艺厂在本周实际生产工艺品的数量．
解：（1）由表格可得，周一生产的工艺品的数量是：300+5＝305（个）
即该厂星期一生产工艺品的数量305个；
（2）本周产量中最多的一天是星期六，最少的一天是星期五，16+300﹣[（﹣10）+300]＝26个，
即本周产量中最多的一天比最少的一天多生产26个；
（3）2100+[5+（﹣2）+（﹣5）+15+（﹣10）+16+（﹣9）]
＝2100+10
＝2110（个）．
即该工艺厂在本周实际生产工艺品的数量是2110个．
【点评】本题考查正数和负数，解题的关键是明确正数和负数在题目中的含义．
23．九月十四金秋大型商品交易会（俗称九月十四）是我县传统节日．今年小汀州一家逛九月十四时，小汀州的妈妈发现商场销售一种茶具和茶碗在开展促销活动，茶具每套定价200元，茶碗每只定价20元，活动期间向小汀州的妈妈提供两种优惠方案，方案一：买一套茶具送一只茶碗；方案二，茶具和茶碗按定价的九五折付款，现在小汀州的妈妈要到商场购买茶具30套，茶碗x只（x＞30）．
（1）若小汀州的妈妈按方案一，需要付款 （20x+5400） 元；若小汀州的妈妈按方案二，需要付款 （19x+5700） 元．（用含x的代数式表示）
（2）若x＝40，试通过计算说明此时小汀州的妈妈选哪种购买方案比较合适？
【分析】（1）由题意分别求出两种方案购买的费用即可；
（2）将x＝40分别代入（1）中所求的代数式，再比较哪个更优惠即可．
解：（1）若小汀州的妈妈按方案一，需要付款30×200+20（x﹣30）＝（20x+5400）元；
若小汀州的妈妈按方案二，需要付款30×200×0.95+20x×0.95＝（19x+5700）元；
故答案为：（20x+5400）；（19x+5700）；
（2）当x＝40时，
方案一：20x+5400＝800+5400＝6200元，
方案二：19x+5700＝760+5700＝6460元，
因为6200＜6460，
所以小汀州的妈妈选方案一更合适．
【点评】本题考查列代数式和代数式求值，解题的关键是理解题意，正确列出代数式．
24．为响应国家“乡村振兴”的号召，张林回家乡承包了一片土地用于种植草莓．土地平面示意图如下（图中长度单位：米），请根据示意图回答下列问题：
（1）用含a、b的式子表示出这片土地的总面积S；
（2）由于草莓品种和各个地块土壤条件存在差异，地块①和地块②平均每平方米可种植9株草莓，剩下地块平均每平方米可种植11株草莓，则张林总共可种植多少株草莓？（用含a、b的式子表示）
（3）在满足（2）问的条件下，当a＝20、b＝15时，张林种植草莓的数量为多少株？
【分析】（1）利用拼凑法，用大长方形的面积减去缺少的小长方形的面积，计算即可得出答案；
（2）首先计算出地块①和地块②的面积，进而得出地块①和地块②可种植的草莓数，然后再计算出除地块①和地块②剩下地块的面积，进而得出除地块①和地块②剩下地块可种植的草莓数，然后再把地块①和地块②可种植的草莓数加上除地块①和地块②剩下地块可种植的草莓数，即可得出答案；
（3）把a＝20、b＝15代入（2）的结论，计算即可得出答案．
解：（1）这片土地的总面积S＝40×（a+30）﹣b×（40﹣16﹣20）＝40a﹣4b+1200（平方米）；
（2）地块①的面积为40a平方米；
地块②的面积为：（30﹣b）×（40﹣20）＝600﹣20b（平方米），
∵地块①和地块②平均每平方米可种植9株草莓，
∴地块①和地块②可种植的草莓为：（40a+600﹣20b）×9＝360a﹣180b+5400（株），
∵除地块①和地块②剩下地块的面积为：40a﹣4b+1200﹣40a﹣600+20b＝600+16b（平方米），
又∵剩下地块平均每平方米可种植11株草莓，
∴除地块①和地块②剩下地块可种植的草莓为：（600+16b）×11＝6600+176b（株），
∴张林总共可种植的草莓为：360a﹣180b+5400+6600+176b＝360a﹣4b+12000（株）；
（3）当a＝20、b＝15时，
360a﹣4b+12000
＝360×20﹣4×15+12000
＝19140，
∴张林种植草莓的数量为19140株．
【点评】本题考查了整式的加减法的应用、求代数式的值，掌握整式的加减法法则，得出所求的面积是关键．
25．已知|a+1|+（b﹣4）2＝0，c＝2a，且a，b，c分别是点A，B，C在数轴上对应的数．
（1）a，b，c的值分别为a＝ ﹣1 ，b＝ 4 ，c＝ ﹣2 ，并在数轴上标出点A，B，C；
（2）定义：在数轴上，若点D到点E、F的距离之和为6，则点D叫做E和F的“幸福中心”．
①若点G是B和C的“幸福中心”，且点G表示的数是整数，求所有满足条件的点G表示的数之和；
②点Q表示7，点P从点Q出发，以每秒2个单位长度的速度向左运动，同时，点M，N分别从点A，B出发，以每秒1个单位长度的速度向右运动，经过多少秒时，点P是M和N的“幸福中心”？
【分析】（1）由|a+1|+（b﹣4）2＝0，根据非负数的性质可求得a＝﹣1，b＝4，由c＝2a，，得c＝﹣2，所以点A，B，C对应的数分别为﹣1，4，﹣2，在数轴上标出点A、B、C即可；
（2）①设点G表示的数是x，点G到点B、C的距离之和为m，先说明点G不能在点C的左侧和点B的右侧，而当点G在点B与点C之间时，m＝x+2+4﹣x＝6，此时﹣2≤x≤4，而x为整数，则x＝﹣2，﹣1，0，1，2，3，4，即可求得所有满足条件的点G表示的数之和是7；
②先说明点M和点N之间的距离保持不变，为4﹣（﹣1）＝5，则点P不能在点M与点N之间，再设运动的时间为t秒，则点P、M、N表示的数分别为7﹣2t、﹣1+t、4+t，当点P在点N的右侧时，则7﹣2t﹣（﹣1+t）+7﹣2t﹣（4+t）＝6；当点P在点M的左侧时，则﹣1+t﹣（7﹣2t）+4+t﹣（7﹣2t）＝6，解方程求出相应的t值即可．
解：（1）∵|a+1|≥0，（b﹣4）2≥0，且|a+1|+（b﹣4）2＝0，
∴|a+1|＝0，（b﹣4）2＝0，
解得a＝﹣1，b＝4；
∵c＝2a，
∴c＝﹣2，
在数轴上点A，B，C如图所示，
故答案为：﹣1，4，﹣2；
（2）①设点G表示的数是x，点G到点B、C的距离之和为m，
若点G在点C左侧，则x＜﹣2，
∴m＝﹣2﹣x+4﹣x＝2﹣2x＞6，不符合题意；
若点G在点B右侧，则x＞4，
∴m＝x+2+x﹣4＝2x﹣2＞6，不符合题意；
当点G在点B与点C之间，则m＝x+2+4﹣x＝6，
∵﹣2≤x≤4，且x为整数，
∴x＝﹣2，﹣1，0，1，2，3，4，
∴﹣2﹣1+0+1+2+3+4＝7，
∴所有满足条件的点G表示的数之和是7；
②∵点M和点N的速度相同，运动方向相同，
∴点M和点N之间的距离保持不变，为4﹣（﹣1）＝5，
若点P在点M与点N之间，由点P到点M、N的距离之和为5，不符合题意，
设运动的时间为t秒，则点P、M、N表示的数分别为7﹣2t、﹣1+t、4+t，
当点P在点N的右侧时，则7﹣2t﹣（﹣1+t）+7﹣2t﹣（4+t）＝6，
解得t＝；
当点P在点M的左侧时，则﹣1+t﹣（7﹣2t）+4+t﹣（7﹣2t）＝6，
解得t＝，
综上所述，经过秒或秒，点P是M和N的“幸福中心”．
【点评】此题重点考查一元一次方程的解法、列一元一次方程解应用题、非负数的性质、数轴上的动点问题的求解等知识与方法，正确地用代数式表示运动过程中点所对应的数是解题的关键．
星期
一
二
三
四
五
六
日
增减（单位：个）
+5
﹣2
﹣5
+15
﹣10
+16
﹣9
星期
一
二
三
四
五
六
日
增减（单位：个）
+5
﹣2
﹣5
+15
﹣10
+16
﹣9