2023-2024学年广西崇左市宁明县九年级（上）期中数学试卷（含解析）

这是一份2023-2024学年广西崇左市宁明县九年级（上）期中数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．在下列关于x的函数中，一定是二次函数的是（ ）
A．y＝x2B．y＝ax2+bx+c
C．y＝8xD．y＝x2（1+x）
2．下列各点在函数y＝﹣的图象上的是（ ）
A．（2，1）B．（﹣2，0）C．（2，0）D．（﹣2，1）
3．抛物线y＝2（x﹣1）2+3的对称轴为（ ）
A．直线x＝1B．直线y＝1C．直线y＝﹣1D．直线x＝﹣1
4．下列说法中，错误的是（ ）
A．等边三角形都相似
B．等腰直角三角形都相似
C．矩形都相似
D．正方形都相似
5．若，则等于（ ）
A．B．C．D．
6．函数y＝（2m﹣1）x是反比例函数，在第一象限内y随x的增大而减小，则m＝（ ）
A．﹣3B．﹣1C．1D．3
7．一枚炮弹射出x秒后的高度为y米，且y与x之间的关系为y＝ax2+bx+c（a≠0）若此炮弹在第3.2秒与第5.8秒时的高度相等，则在下列时间中炮弹所在高度最高的是（ ）
A．第3.3秒B．第4.5秒C．第5.2秒D．第4.3秒
8．在平面直角坐标系中，将抛物线y＝x2+4x+3平移后与抛物线y＝x2重合，则下列平移符合要求的是（ ）
A．向右平移2个单位，向下平移1个单位
B．向右平移2个单位，向上平移1个单位
C．向左平移2个单位，向下平移1个单位
D．向左平移2个单位，向上平移1个单位
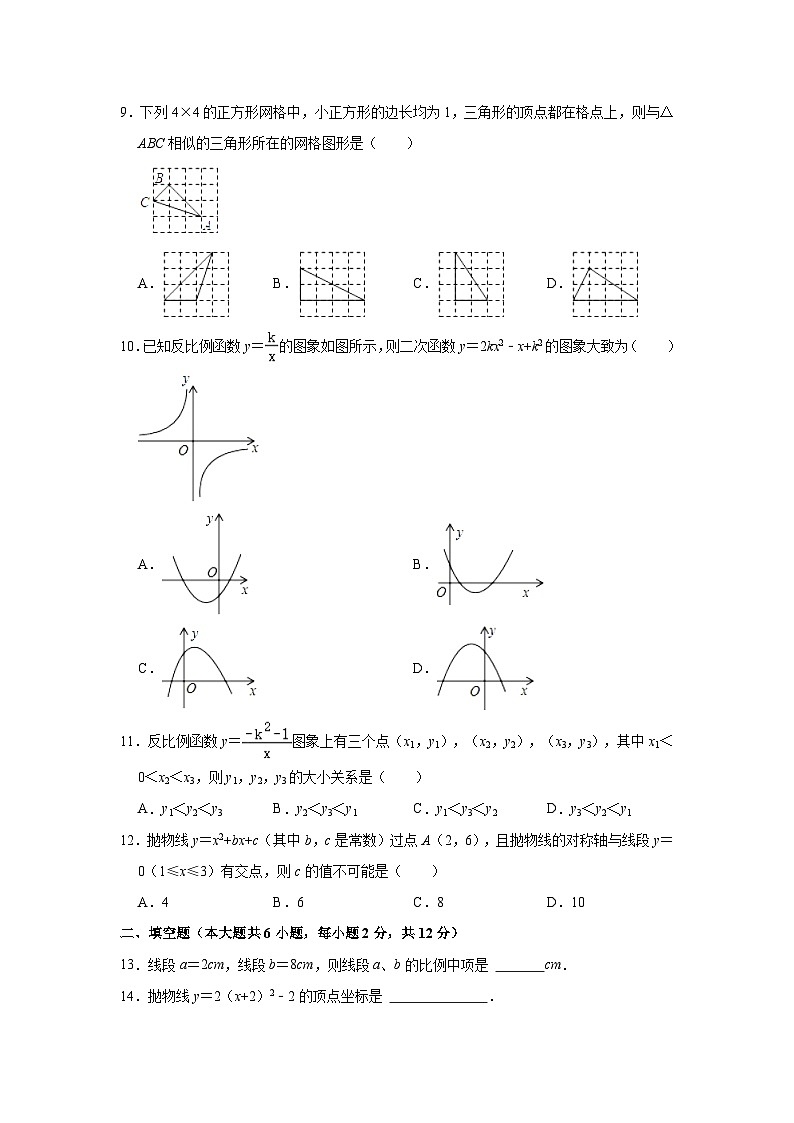
9．下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是（ ）
A．B．C．D．
10．已知反比例函数y＝的图象如图所示，则二次函数y＝2kx2﹣x+k2的图象大致为（ ）
A．B．
C．D．
11．反比例函数y＝图象上有三个点（x1，y1），（x2，y2），（x3，y3），其中x1＜0＜x2＜x3，则y1，y2，y3的大小关系是（ ）
A．y1＜y2＜y3B．y2＜y3＜y1C．y1＜y3＜y2D．y3＜y2＜y1
12．抛物线y＝x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y＝0（1≤x≤3）有交点，则c的值不可能是（ ）
A．4B．6C．8D．10
二、填空题（本大题共6小题，每小题2分，共12分）
13．线段a＝2cm，线段b＝8cm，则线段a、b的比例中项是 cm．
14．抛物线y＝2（x+2）2﹣2的顶点坐标是 ．
15．如图，已知∠A＝∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是 ．（只需写一个条件，不添加辅助线和字母）
16．如图是反比例函数y＝的图象上的一点，过A作AB⊥x轴，垂足为B．已知△AOB面积为3，则这个反比例函数的关系式为 ．
17．已知线段AB＝1cm，C是AB的黄金分割点，且AC＞BC，那么AC＝ cm．
18．在平面直角坐标系xOy中，若函数y＝kx2+2x+1的图象与x轴只有一个交点，则k＝ ．
三、解答题（本大题共8小题，满分72分.解答题应写出文字说明、证明过程或演算步骤.）
19．已知抛物线y＝ax2+bx﹣3（a≠0）经过点（﹣1，0），（3，0），求a，b的值．
20．若，且3x+2y﹣z＝14，求x，y，z的值．
21．如图，AB＝3AC，BD＝3AE，又BD∥AC，点B，A，E在同一条直线上．求证：△ABD∽△CAE．
22．已知二次函数y＝﹣x2+2x﹣m（m是常数）．
（1）若该二次函数的图象与x轴有两个不同的交点，求m的取值范围；
（2）若该二次函数的图象与x轴的其中一个交点坐标为（﹣1，0），求一元二次方程﹣x2+2x﹣m＝0的解．
23．如图，一次函数y＝2x﹣2的图象与反比例函数y＝的图象交于M，N两点．
（1）求反比例函数的表达式；
（2）求△OMN的面积；
（3）根据图象，直接写出使反比例函数值大于一次函数值时x的取值范围．
24．某商场销售一种商品，进价为每个20元，规定每个商品售价不低于进价，且不高于60元，经调查发现，每天的销售量y（个）与每个商品的售价x（元）满足一次函数关系，其部分数据如下所示：
（1）求y与x之间的函数表达式；
（2）设商场每天获得的总利润为w（元），求w与x之间的函数表达式；
（3）不考虑其他因素，当商品的售价为多少元时，商场每天获得的总利润最大，最大利润是多少？
25．如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F．试问：
（1）图中△APD与哪个三角形全等？并说明理由．
（2）求证：PC2＝PE•PF．
26．已知在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴相交于点A，B，与y轴相交于点C，直线y＝x+4经过A，C两点，
（1）求抛物线的表达式；
（2）如果点P，Q在抛物线上（P点在对称轴左边），且PQ∥AO，PQ＝2AO，求P，Q的坐标；
（3）动点M在直线y＝x+4上，且△ABC与△COM相似，求点M的坐标．
参考答案
一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑.）
1．在下列关于x的函数中，一定是二次函数的是（ ）
A．y＝x2B．y＝ax2+bx+c
C．y＝8xD．y＝x2（1+x）
【分析】根据二次函数的定义：y＝ax2+bx+c（a≠0且a是常数），可得答案．
解：A、y＝x2是二次函数，故A符合题意；
B、a＝0时是一次函数，故B不符合题意，
C、y＝8x是一次函数，故C不符合题意；
D、y＝x2（1+x）不是二次函数，故D不符合题意；
故选：A．
【点评】本题考查了二次函数的定义，利用二次函数的定义是解题关键，注意a是不等于零的常数．
2．下列各点在函数y＝﹣的图象上的是（ ）
A．（2，1）B．（﹣2，0）C．（2，0）D．（﹣2，1）
【分析】根据反比例函数图象上点的坐标特征即可求解．
解：∵函数解析式为y＝﹣，
把四个选项的坐标依次代入函数解析式，仅选项D的坐标（﹣2，1）在函数y＝﹣的图象上，
∴D选项符合题意，A、B、C选项不符合题意，
故选：D．
【点评】本题考查了反比例函数图象上点的坐标特征，解题的关键是把四个选项的坐标依次代入函数解析式即可得出正确答案．
3．抛物线y＝2（x﹣1）2+3的对称轴为（ ）
A．直线x＝1B．直线y＝1C．直线y＝﹣1D．直线x＝﹣1
【分析】根据函数的顶点式可以直接写出抛物线的对称轴，本题得以解决．
解：∵y＝2（x﹣1）2+3，
∴该抛物线的对称轴是直线x＝1，
故选：A．
【点评】本题考查二次函数的性质，解答本题的关键是明确题意，利用二次函数的性质解答．
4．下列说法中，错误的是（ ）
A．等边三角形都相似
B．等腰直角三角形都相似
C．矩形都相似
D．正方形都相似
【分析】根据相似三角形的判定及相似多边形的定义作答．
解：A、由于等边三角形的每个角都等于60°，根据有两角对应相等的两三角形相似，知等边三角形都相似正确，故选项错误；
B、由于任意一个等腰直角三角形的三个内角的度数是45°，45°，90°，根据有两角对应相等的两三角形相似，知等腰直角三角形都相似正确，故选项错误；
C、由于矩形对应边的比不一定相等，根据相似多边形的定义知矩形都相似，不正确，故选项正确；
D、由于正方形的每个角都相等，每条边也相等，根据相似多边形的定义知正方形都相似正确，故选项错误．
故选：C．
【点评】有两角对应相等的两三角形相似．如果两个多边形满足对应角相等，对应边的比相等，那么这两个多边形相似．
5．若，则等于（ ）
A．B．C．D．
【分析】根据比例的性质进行计算，即可解答．
解：∵，
∴＝1﹣＝1﹣＝，
故选：A．
【点评】本题考查了比例的性质，准确熟练地进行计算是解题的关键．
6．函数y＝（2m﹣1）x是反比例函数，在第一象限内y随x的增大而减小，则m＝（ ）
A．﹣3B．﹣1C．1D．3
【分析】根据反比例函数的定义列出方程求解，再根据它的性质决定解的取舍．
解：根据题意得：，
解得：m＝1．
故选：C．
【点评】本题考查了反比例函数的性质．对于反比例函数y＝，当k＞0时，在每一个象限内，函数值y随自变量x的增大而减小；当k＜0时，在每一个象限内，函数值y随自变量x增大而增大．
7．一枚炮弹射出x秒后的高度为y米，且y与x之间的关系为y＝ax2+bx+c（a≠0）若此炮弹在第3.2秒与第5.8秒时的高度相等，则在下列时间中炮弹所在高度最高的是（ ）
A．第3.3秒B．第4.5秒C．第5.2秒D．第4.3秒
【分析】由炮弹在第3.2秒与第5.8秒时的高度相等可知这两点关于对称轴对称，故此可求得求得抛物线的对称轴．
解：∵炮弹在第3.2秒与第5.8秒时的高度相等，
∴抛物线的对称轴为x＝4.5．
故选：B．
【点评】本题主要考查的是二次函数的应用，利用抛物线的对称性求得对称轴方程是解题的关键．
8．在平面直角坐标系中，将抛物线y＝x2+4x+3平移后与抛物线y＝x2重合，则下列平移符合要求的是（ ）
A．向右平移2个单位，向下平移1个单位
B．向右平移2个单位，向上平移1个单位
C．向左平移2个单位，向下平移1个单位
D．向左平移2个单位，向上平移1个单位
【分析】先确定抛物线y＝x2+4x+3的顶点坐标为（﹣2，﹣1），根据点平移的规律，点（﹣2，﹣1）向左平移2个单位，再向上平移1个单位得到对应点的坐标为（0，0），即将抛物线y＝x2+4x+3向左平移2个单位，向上平移1个单位与抛物线y＝x2重合，
解：∵y＝x2+4x+3＝（x+2）2﹣1，
∴抛物线y＝x2+4x+3的顶点为（﹣2，﹣1），抛物线y＝x2的顶点为（0，0），
∵点（﹣2，﹣1）向右平移2个单位，再向上平移1个单位得到对应点的坐标为（0，0），
∴将抛物线y＝x2+4x+3向左平移2个单位，向上平移1个单位得到将抛物线y＝x2．
故选：B．
【点评】本题考查了二次函数的图象与几何变换，熟练掌握平移的规律：左加右减，上加下减是解题的关键．
9．下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是（ ）
A．B．C．D．
【分析】根据勾股定理求出△ABC的三边，并求出三边之比，然后根据网格结构利用勾股定理求出三角形的三边之比，再根据三边对应成比例，两三角形相似选择答案．
解：根据勾股定理，AB＝＝2，
BC＝＝，
AC＝＝，
所以△ABC的三边之比为：2：＝1：2：，
A、三角形的三边分别为2，＝，＝3，三边之比为2：：3＝：：3，故A选项错误；
B、三角形的三边分别为2，4，＝2，三边之比为2：4：2＝1：2：，故B选项正确；
C、三角形的三边分别为2，3，＝，三边之比为2：3：，故C选项错误；
D、三角形的三边分别为＝，＝，4，三边之比为：：4，故D选项错误．
故选：B．
【点评】本题主要考查了相似三角形的判定与网格结构的知识，根据网格结构分别求出各三角形的三条边的长，并求出三边之比是解题的关键．
10．已知反比例函数y＝的图象如图所示，则二次函数y＝2kx2﹣x+k2的图象大致为（ ）
A．B．
C．D．
【分析】本题可先由反比例函数的图象得到字母系数的正负，再与二次函数的图象相比较看是否一致．
解：∵函数y＝的图象经过二、四象限，∴k＜0，
∴抛物线开口向下，对称轴x＝﹣＝＜0，
即对称轴在y轴的左边．
故选：D．
【点评】本题将二次函数与反比例函数综合在一起进行考查，增加了题目的研究性，也是中考中的热点题型．
11．反比例函数y＝图象上有三个点（x1，y1），（x2，y2），（x3，y3），其中x1＜0＜x2＜x3，则y1，y2，y3的大小关系是（ ）
A．y1＜y2＜y3B．y2＜y3＜y1C．y1＜y3＜y2D．y3＜y2＜y1
【分析】先根据反比例函数y＝的系数﹣k2﹣1＜0判断出函数图象在二、四象限，在每个象限内，y随x的增大而增大，再根据x1＜0＜x2＜x3，判断出y1、y2、y3的大小．
解：∵反比例函数y＝中，﹣k2﹣1＜0，
∴此函数的图象在二、四象限，在每一象限内y随x的增大而增大，
∵x1＜0＜x2＜x3，
∴y1＞0、y2＜y3＜0，
∴y2＜y3＜y1．
故选：B．
【点评】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数的图象与系数的关系及反比例函数的增减性是解答此题的关键．
12．抛物线y＝x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y＝0（1≤x≤3）有交点，则c的值不可能是（ ）
A．4B．6C．8D．10
【分析】根据抛物线y＝x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y＝0（1≤x≤3）有交点，可以得到c的取值范围，从而可以解答本题．
解：∵抛物线y＝x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y＝0（1≤x≤3）有交点，
∴
解得6≤c≤14，
故选：A．
【点评】本题考查二次函数的性质、解不等式，解题关键是明确题意，列出相应的关系式．
二、填空题（本大题共6小题，每小题2分，共12分）
13．线段a＝2cm，线段b＝8cm，则线段a、b的比例中项是 4 cm．
【分析】比例的基本性质：两外项之积等于两内项之积．
解：根据比例中项的概念结合比例的基本性质得：比例中项的平方等于两条线段的乘积．
设它们的比例中项是x cm，则
x2＝2×8，
解得x＝±4（线段是正数，负值舍去）．
故答案为：4．
【点评】本题考查了比例中项的概念，注意：求两条线段的比例中项的时候，应舍去负数．
14．抛物线y＝2（x+2）2﹣2的顶点坐标是 （﹣2，﹣2） ．
【分析】根据二次函数顶点式的特征解答即可．
解：∵二次函数顶点式y＝a（x﹣h）2+k的顶点坐标为：（h，k），
∴抛物线y＝2（x+2）2﹣2的顶点坐标是（﹣2，﹣2）．
故答案为：（﹣2，﹣2）．
【点评】本题考查了二次函数的顶点式，熟练掌握顶点式的特征是解答本题的关键．
15．如图，已知∠A＝∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是 AB∥DE ．（只需写一个条件，不添加辅助线和字母）
【分析】根据有两组角对应相等的两个三角形相似进行添加条件．
解：∵∠A＝∠D，
∴当∠B＝∠DEF时，△ABC∽△DEF，
∵AB∥DE时，∠B＝∠DEF，
∴添加AB∥DE时，使△ABC∽△DEF．
故答案为AB∥DE．
【点评】本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似．
16．如图是反比例函数y＝的图象上的一点，过A作AB⊥x轴，垂足为B．已知△AOB面积为3，则这个反比例函数的关系式为 y＝﹣ ．
【分析】根据反比例函数的比例系数k的几何意义得到 |k|＝3，然后去绝对值即可得到满足条件的k的值．
解：∵AB⊥x轴，
∴S△OAB＝|k|，
∵△OAB的面积为3，
∴|k|＝3，
∵k＜0，
∴k＝﹣6．
∴这个反比例函数的表达式为y＝﹣，
故答案为y＝﹣．
【点评】本题考查了待定系数法求反比例函数的解析式，反比例函数的比例系数k的几何意义：在反比例函数y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
17．已知线段AB＝1cm，C是AB的黄金分割点，且AC＞BC，那么AC＝ cm．
【分析】根据黄金分割点的定义，知AC为较长线段，则AC＝AB，即可求解．
解：∵线段AB＝1cm，C是AB的黄金分割点，且AC＞BC，
∴AC＝AB＝×1＝（cm），
故答案为：．
【点评】本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC＝AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中AC＝AB≈0.618AB，并且线段AB的黄金分割点有两个．
18．在平面直角坐标系xOy中，若函数y＝kx2+2x+1的图象与x轴只有一个交点，则k＝ 0或1 ．
【分析】依据题意，对于k进行分类讨论，①k＝0，符合题意；②k≠0，根据二次函数的图象与性质，由Δ＝0进行计算可以得解．
解：由题意，①当k＝0时，函数为y＝2x+1与x轴交于（﹣，0）一个交点，符合题意．
②k≠0，函数是二次函数，根据二次函数的图象与性质，
∴Δ＝4﹣4k＝0．
∴k＝1．
综上，k＝0或1．
故答案为：0或1．
【点评】本题主要考查了抛物线与x轴的交点，一次函数与x轴的交点坐标，把求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．
三、解答题（本大题共8小题，满分72分.解答题应写出文字说明、证明过程或演算步骤.）
19．已知抛物线y＝ax2+bx﹣3（a≠0）经过点（﹣1，0），（3，0），求a，b的值．
【分析】根据抛物线y＝ax2+bx﹣3（a≠0）经过点（﹣1，0），（3，0），可以求得a、b的值，本题得以解决．
解：∵抛物线y＝ax2+bx﹣3（a≠0）经过点（﹣1，0），（3，0），
∴，
解得，
，
即a的值是1，b的值是﹣2．
【点评】本题考查二次函数图象上点的坐标特征，解答本题的关键是明确题意，利用二次函数的性质解答．
20．若，且3x+2y﹣z＝14，求x，y，z的值．
【分析】首先设恒等式等于一个常数，然后得到x，y，z与这个常数的关系式，再代入3x+2y﹣z＝14中进行求解．
解：设＝k，
则x＝2k，y＝3k，z＝5k，
∴6k+6k﹣5k＝14，
∴k＝2，
∴x＝4，y＝6，z＝10．
答：x，y，z的值分别为4，6，10．
【点评】设恒等式等于一个常数，然后得到x，y，z与这个常数的关系式是解答本题的关键．
21．如图，AB＝3AC，BD＝3AE，又BD∥AC，点B，A，E在同一条直线上．求证：△ABD∽△CAE．
【分析】由平行线的性质可得∠EAC＝∠ABD，由线段关系可得，可得结论．
【解答】证明：∵BD∥AC，
∴∠EAC＝∠ABD，
∵AB＝3AC，BD＝3AE，
∴，
∴△ABD∽△CAE．
【点评】本题考查了相似三角形的判定，掌握相似三角形的判定方法是解题的关键．
22．已知二次函数y＝﹣x2+2x﹣m（m是常数）．
（1）若该二次函数的图象与x轴有两个不同的交点，求m的取值范围；
（2）若该二次函数的图象与x轴的其中一个交点坐标为（﹣1，0），求一元二次方程﹣x2+2x﹣m＝0的解．
【分析】（1）根据二次函数图象与x轴有两个不同的交点，得出Δ＞0，求出m的取值范围．
（2）代入（﹣1，0），求出m，再解方程即可．
解：（1）∵二次函数y＝﹣x2+2x﹣m的图象与x轴有两个不同的交点，
∴一元二次方程﹣x2+2x﹣m＝0有两个不相等的实数根，
∴Δ＞0，即22﹣4×（﹣1）×（﹣m）＞0，解得m＜1；
（2）二次函数y＝﹣x2+2x﹣m的图象与x轴的其中一个交点坐标为（﹣1，0），
∴﹣1﹣2﹣m＝0，解得m＝﹣3，
∴一元二次方程﹣x2+2x﹣m＝0为﹣x2+2x+3＝0，解得x＝﹣1或3．
【点评】本题考查了二次函数与x轴交点个数与△的关系，待定系数法求解析式．需注意计算细节．
23．如图，一次函数y＝2x﹣2的图象与反比例函数y＝的图象交于M，N两点．
（1）求反比例函数的表达式；
（2）求△OMN的面积；
（3）根据图象，直接写出使反比例函数值大于一次函数值时x的取值范围．
【分析】（1）先把N点坐标代入y＝，利用待定系数法即可求得反比例函数解析式；
（2）利用反比例函数解析式确定M点的坐标为（2，2），然后利用待定系数法求一次函数解析式，即可求出P点的坐标，再根据三角形的面积公式求出三角形POM和三角形PON的面积，相加即可得出答案；
（3）观察函数图象得到当0＜x＜2或x＜﹣1时，反比例函数图象都在一次函数图象下方，即反比例函数的值小于一次函数的值．
解：（1）把N（﹣1，﹣4）代入y＝，
得k＝﹣1×（﹣4）＝4，
所以反比例函数解析式为y＝；
（2）把M（2，m）代入y＝，
得2m＝4，解得m＝2，
则M点的坐标为（2，2）．
把M（2，2），N（﹣1，﹣4）代入y＝ax+b，得，
解得，
所以一次函数解析式为y＝2x﹣2，
设直线与x轴的交点为P，则P（1，0），即OP＝1，
∴S△MON＝S△MOP+S△NOP＝×1×2+×1×4＝3；
（3）由图象可知，当0＜x＜2或x＜﹣1时，反比例函数的值大于一次函数的值．
【点评】本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式，三角形的面积以及观察函数图象的能力．
24．某商场销售一种商品，进价为每个20元，规定每个商品售价不低于进价，且不高于60元，经调查发现，每天的销售量y（个）与每个商品的售价x（元）满足一次函数关系，其部分数据如下所示：
（1）求y与x之间的函数表达式；
（2）设商场每天获得的总利润为w（元），求w与x之间的函数表达式；
（3）不考虑其他因素，当商品的售价为多少元时，商场每天获得的总利润最大，最大利润是多少？
【分析】（1）待定系数法求解可得；
（2）根据“总利润＝每千克利润×销售量”可得函数解析式；
（3）将所得函数解析式配方成顶点式即可得最值情况．
解：（1）设y与x之间的函数解析式为y＝kx+b，
则，
解得，
即y与x之间的函数表达式是y＝﹣2x+160；
（2）由题意可得，w＝（x﹣20）（﹣2x+160）＝﹣2x2+200x﹣3200，
即w与x之间的函数表达式是w＝﹣2x2+200x﹣3200；
（3）∵w＝﹣2x2+200x﹣3200＝﹣2（x﹣50）2+1800，20≤x≤60，
∴当20≤x≤50时，w随x的增大而增大；
当50≤x≤60时，w随x的增大而减小；
当x＝50时，w取得最大值，此时w＝1800元
即当商品的售价为50元时，商场每天获得的总利润最大，最大利润是1800．
【点评】本题主要考查二次函数的应用，解题的关键是熟练掌握待定系数法求函数解析式及二次函数的性质．
25．如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F．试问：
（1）图中△APD与哪个三角形全等？并说明理由．
（2）求证：PC2＝PE•PF．
【分析】（1）由菱形的性质可知：∠CDP＝∠ADP，DC＝AD，又因为PD＝PD，所以△APD全等△CPD；
（2）首先证明∠DAP＝∠AFP，从而得到△EPA∽△APE，故PA2＝PE•PF，因为PC＝PA，所以PC2＝PE•PF．
解：（1）△APD≌△CPD．
理由：∵四边形ABCD为菱形，
∴∠CDP＝∠ADP，DC＝AD．
在△APD和△CPD中，，
∴△APD≌△CPD．
（2）∵△APD≌△CPD，
∴∠DCP＝∠DAP，PC＝PA．
∵DC∥AB，
∴∠DCP＝∠AFP．
∴∠DAP＝∠AFP．
又∵∠FPA＝∠APE，
∴△EPA∽△APE．
∴.，即PA2＝PE•PF．
∴PC2＝PE•PF．
【点评】本题主要考查的是全等三角形的性质和判定、相似三角形的性质和判定，证得∠DAP＝∠AFP是解题的关键．
26．已知在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴相交于点A，B，与y轴相交于点C，直线y＝x+4经过A，C两点，
（1）求抛物线的表达式；
（2）如果点P，Q在抛物线上（P点在对称轴左边），且PQ∥AO，PQ＝2AO，求P，Q的坐标；
（3）动点M在直线y＝x+4上，且△ABC与△COM相似，求点M的坐标．
【分析】（1）根据直线y＝x+4求点A、C的坐标，再利用待定系数法求二次函数的表达式；
（2）由PQ∥AO可知，P、Q关于对称轴x＝﹣1对称，由PQ＝2AO＝8，可得点P、Q两点的横坐标，代入抛物线的解析式中可得两点的坐标；
（3））因为∠MCO＝∠CAB＝45°，所以△ABC与△COM相似，分两种情况：
①当△MCO∽△CAB时，如图1，列比例式可求得CM的长，从而得出M的坐标；
②当△OCM∽△CAB时，如图2，列比例式可求得CM的长，从而得出M的坐标．
解：（1）当x＝0时，y＝4，即C（0，4），
当y＝0时，x＝﹣4，即A（﹣4，0），
将A、C两点的坐标代入抛物线y＝﹣x2+bx+c中得：
，解得：，
∴抛物线的表达式为：y＝﹣x2﹣x+4；
（2）由题意得：PQ＝2AO＝8，
又PQ∥AO，即P、Q关于对称轴x＝﹣1对称，
∴PQ＝8，﹣1﹣4＝﹣5，
当x＝﹣5时，y＝+4＝﹣，即P（﹣5，﹣），
﹣1+4＝3，即Q（3，﹣），
∴P的坐标为（﹣5，﹣），Q的坐标为（3，﹣）；
（3）∵A（﹣4，0），对称轴是：x＝﹣1，
∴B（2，0），
∴AB＝2+4＝6，
∵∠MCO＝∠CAB＝45°，
由勾股定理得：AC＝＝4，BC＝＝2，
①当△MCO∽△CAB时，如图1，
∴＝，即，
∴CM＝，
过M作MH⊥y轴于H，
∴MH＝CH＝＝，
当x＝﹣时，y＝﹣+4＝，
∴M（﹣，），
②当△OCM∽△CAB时，如图2，
，即＝，
∴CM＝3，
过M作MH⊥y轴于H，
MH＝CH＝＝3，
当x＝﹣3时，y＝﹣3+4＝1，
∴M（﹣3，1），
综上所述，点M的坐标是：（﹣，）或（﹣3，1）．
【点评】本题是二次函数的综合题，考查了利用待定系数法求二次函数的解析式、抛物线的轴对称性、三角形相似的性质和判定，难度适中，采用了分类讨论的思想，利用已知的相似列比例式，并与一次函数相结合，求出点M的坐标，使问题得以解决．
每个商品的售价x（元）
…
30
40
50
…
每天的销售量y（个）
…
100
80
60
…
每个商品的售价x（元）
…
30
40
50
…
每天的销售量y（个）
…
100
80
60
…