预测07 相似三角形（四种基本模型专练）-2023-2024学年九年级数学上学期期末考点预测（人教版）

这是一份预测07 相似三角形（四种基本模型专练）-2023-2024学年九年级数学上学期期末考点预测（人教版），文件包含猜想07相似三角形四种基本模型专练原卷版docx、猜想07相似三角形四种基本模型专练解析版docx等2份试卷配套教学资源，其中试卷共130页， 欢迎下载使用。
题型一：“8”字模型相似三角形
题型二：“A”字模型相似三角形
题型三：一线三等角构造相似模型
题型四：手拉手模型-旋转型相似
题型一：“8”字模型相似三角形
一．选择题（共6小题）
1．（2023春•荣成市期末）四分仪是一种十分古老的测量仪器．其出现可追溯到数学家托勒密的《天文学大成》．图1是古代测量员用四分仪测量一方井的深度，将四分仪置于方井上的边沿，通过窥衡杆测望井底点F、窥衡杆与四分仪的一边BC交于点H．图2中，四分仪为正方形ABCD．方井为矩形BEFG．若测量员从四分仪中读得AB为1，BH为0.5，实地测得BE为2.5．则井深BG为（ ）
A．4B．5C．6D．7
【分析】根据正方形的性质可得∠ABC＝90°，再根据矩形的性质可得BG＝EF，∠BEF＝90°，从而可得∠ABH＝∠FEH＝90°，然后证明8字模型相似三角形△ABH∽△FEH，从而利用相似三角形的性质进行计算即可解答．
【解答】解：∵四边形ABCD是正方形，
∴∠ABC＝90°，
∵BE＝2.5，BH＝0.5，
∴HE＝BE﹣BH＝2.5﹣0.5＝2，
∵四边形BEFG是矩形，
∴BG＝EF，∠BEF＝90°，
∴∠ABH＝∠FEH＝90°，
∵∠AHB＝∠EHF，
∴△ABH∽△FEH，
∴＝，
∴＝，
∴EF＝4，
∴BG＝EF＝4，
故选：A．
【点评】本题考查了相似三角形的应用，矩形的性质，正方形的性质，熟练掌握8字模型相似三角形是解题的关键．
2．（2023春•重庆期末）如图，l1∥l2∥l3，直线a，b相交于点G，与这三条平行线分别相交于点A、B、C和点D、E、F，下列比例式中错误的是（ ）
A．B．C．D．
【分析】由平行线分线段成比例定理，相似三角形的判定和性质即可判断．
【解答】解：A、由l1∥l2得到＝，故A正确；
B由l1∥l3得到＝，故B正确；
C、由l2∥l3得到△BGE∽△CGF推出＝，故C错误；
D、由l1∥l2得到△AGD∽△BGE，推出＝，故D正确．
故选：C．
【点评】本题考查平行线分线段成比例，相似三角形的判定和性质，关键是掌握相似三角形的性质，平行线分线段成比例定理．
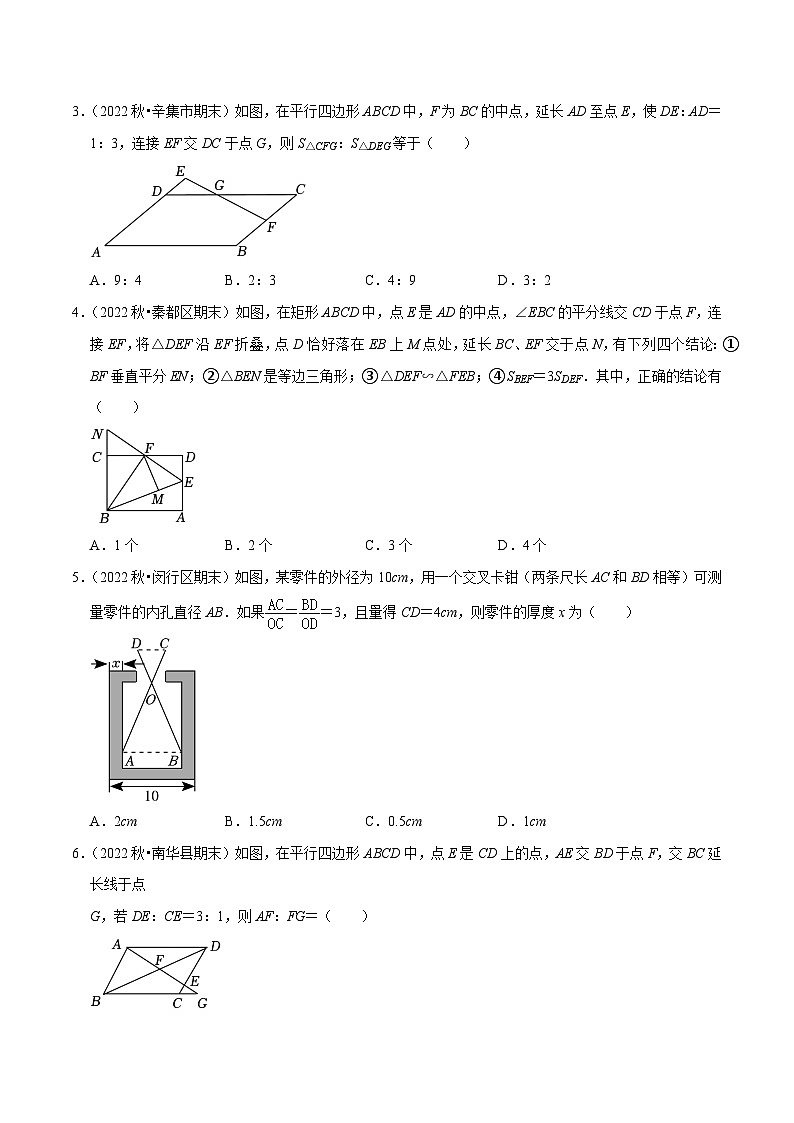
3．（2022秋•辛集市期末）如图，在平行四边形ABCD中，F为BC的中点，延长AD至点E，使DE：AD＝1：3，连接EF交DC于点G，则S△CFG：S△DEG等于（ ）
A．9：4B．2：3C．4：9D．3：2
【分析】利用平行四边形的性质可得AD∥BC，AD＝BC，再根据线段中点的定义可得CF＝BC＝AD，然后证明8字模型相似三角形△EDG∽△FCG，利用相似三角形的性质进行计算即可解答．
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵F为BC的中点，
∴CF＝BC，
∴CF＝AD，
∵AE∥CF，
∴∠E＝∠GFC，∠EDG＝∠C，
∴△EDG∽△FCG，
∵DE：AD＝1：3，
∴DE＝AD，
∴S△CFG：S△DEG＝（）2＝（）2＝（）2＝，
故选：A．
【点评】本题考查了相似三角形的判定与性质，平行四边形的性质，熟练掌握8字模型相似三角形是解题的关键．
4．（2022秋•秦都区期末）如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F，连接EF，将△DEF沿EF折叠，点D恰好落在EB上M点处，延长BC、EF交于点N，有下列四个结论：①BF垂直平分EN；②△BEN是等边三角形；③△DEF∽△FEB；④SBEF＝3SDEF．其中，正确的结论有（ ）
A．1个B．2个C．3个D．4个
【分析】由折叠的性质可得DE＝EM，∠DEF＝∠BEF，∠D＝∠FME＝90°，可证BN＝BE，由等腰三角形的性质可得BF垂直平分EN，故①正确；
若△BEN是等边三角形，由此推出BE＝EF，与题意不符合，所以△BEN不是等边三角形，故②错误；
由两组角对应相等的两个三角形相似，可求△DEF∽△FEB，故③正确；
由“AAS”可证△BFM≌△BFC，可得BE＝3EM，则S△BEF＝3S△EMF＝3S△DEF；故④正确，即可求解．
【解答】解：∵将△DEF沿EF折叠，点D恰好落在EB上M点处，
∴DE＝EM，∠DEF＝∠BEF，∠D＝∠FME＝90°，
∵AD∥BC，
∴∠DEF＝∠N，
∴∠DEF＝∠N＝∠BEN，
∴BN＝BE，
∵BF平分∠EBN，
∴BF垂直平分EN，故①正确；
若△BEN是等边三角形，
∴BE＝EN＝2EF，∠EBN＝∠N＝30°，
∴∠CFN＝∠DFE＝30°＝∠ABE，
∴EF＝2DE，BE＝2AE，
又∵点E是AD的中点，
∴AE＝DE，
∴BE＝EF，与题意不符合，
∴△BEN不是等边三角形，故②错误；
∵BF垂直平分EN，
∴∠BFE＝90°＝∠D，
又∵∠DEF＝∠BEF，
∴△DEF∽△FEB，故③正确；
在△BFM和△BFC中，
，
∴△BFM≌△BFC（AAS），
∴BM＝BC＝AD＝2DE＝2EM．
∴BE＝3EM．
∴S△BEF＝3S△EMF＝3S△DEF；故④正确．
故选：C．
【点评】本题考查了相似三角形的判定，折叠的性质，矩形的性质，角平分线的性质以及全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
5．（2022秋•闵行区期末）如图，某零件的外径为10cm，用一个交叉卡钳（两条尺长AC和BD相等）可测量零件的内孔直径AB．如果＝＝3，且量得CD＝4cm，则零件的厚度x为（ ）
A．2cmB．1.5cmC．0.5cmD．1cm
【分析】根据相似三角形的判定和性质，可以求得AB的长，再根据某零件的外径为10cm，即可求得x的值．
【解答】解：∵＝＝3，∠COD＝∠AOB，
∴△COD∽△AOB，
∴AB：CD＝2，
∵CD＝4cm．
∴AB＝8cm．
∵某零件的外径为10cm，
∴零件的厚度x为：（10﹣8）÷2＝1（cm），
故选：D．
【点评】本题考查相似三角形的应用，解答本题的关键是求出AB的值．
6．（2022秋•南华县期末）如图，在平行四边形ABCD中，点E是CD上的点，AE交BD于点F，交BC延长线于点
G，若DE：CE＝3：1，则AF：FG＝（ ）
A．3：4B．3：5C．9：16D．9：25
【分析】利用平行四边形的性质先说明△ADE∽△GCE，再利用相似三角形的性质用CG表示出AD、BG，再通过△ADF∽△BGF可得结论．
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC．
∴AD∥BG．
∴△ADE∽△GCE．
∴＝＝3．
∴AD＝BC＝3CG．
∴BG＝4CG．
∵AD∥BG，
∴△ADF∽△GBF．
∴＝＝＝．
故选：A．
【点评】本题主要考查了相似三角形，掌握相似三角形的判定和性质及平行四边形的性质是解决本题的关键．
二．填空题（共7小题）
7．（2022秋•香坊区期末）如图，AB∥CD，AC与BD相交于点E，AB＝1，CD＝2，△ABE的面积为1，则△CDE的面积为 4 ．
【分析】根据平行线的性质得∠A＝∠C，∠B＝∠D，则△ABE∽△CDE，根据相似三角形的面积比等于相似比的平方即可求解．
【解答】解：∵AB∥CD，
∴∠A＝∠C，∠B＝∠D，
∴△ABE∽△CDE，
∴，即S△CDE＝4S△ABE，
∵△ABE的面积为1，
∴S△CDE＝4．
故答案为：4．
【点评】本题主要考查平行线的性质、相似三角形的判定与性质，熟练掌握相似三角形的面积比等于相似比的平方是解题关键．
8．（2022秋•如皋市期末）《九章算术》中记载了一种测量古井水面以上部分深度的办法：如图所示，在井口A处立一垂直于井口的木杆AB，从木杆的顶端B观测井水水岸D，视线BD与井口的直径CA交于点E，若测得AB＝1米，AC＝1.6米，AE＝0.4米，则水面以上深度CD为 3米 ．
【分析】根据已知可得CE＝1.2米，再根据题意可得：∠BAC＝∠ACD＝90°，然后证明8字模型相似三角形△AEB∽△CED，从而利用相似三角形的性质，进行计算即可解答．
【解答】解：∵AC＝1.6米，AE＝0.4米，
∴CE＝AC﹣AE＝1.2（米），
由题意得：∠BAC＝∠ACD＝90°，
∵∠AEB＝∠CED，
∴△AEB∽△CED，
∴＝，
∴＝，
解得：CD＝3米，
故答案为：3米．
【点评】本题考查了相似三角形的应用，数学常识，熟练掌握8字模型相似三角形是解题的关键．
9．（2022秋•静安区期末）在矩形ABCD内作正方形AEFD（如图所示），矩形的对角线AC交正方形的边EF于点P．如果点F恰好是边CD的黄金分割点（DF＞FC），且PE＝2，那么PF＝ ﹣1 ．
【分析】先根据黄金分割的定义可得＝，再利用正方形的性质可得：DF∥AE，DF＝AE，从而可得＝，然后证明8字模型相似三角形△CFP∽△AEP，从而利用相似三角形的性质进行计算即可解答．
【解答】解：∵点F恰好是边CD的黄金分割点（DF＞FC），
∴＝＝，
∵四边形AEFD是正方形，
∴DF∥AE，DF＝AE，
∴＝，
∵DC∥AB，
∴∠FCP＝∠PAE，∠CFP＝∠AEP，
∴△CFP∽△AEP，
∴＝＝，
∵PE＝2，
∴PF＝﹣1，
故答案为：﹣1．
【点评】本题考查了相似三角形的判定与性质，矩形的性质，正方形的性质，黄金分割，熟练掌握8字模型相似三角形是解题的关键．
10．（2022秋•黄浦区期末）如图是一个零件的剖面图，已知零件的外径为10cm，为求出它的厚度x，现用一个交叉卡钳（AC和BD的长相等）去测量零件的内孔直径AB．如果＝＝，且量得CD的长是3cm，那么零件的厚度x是 0.5 cm．
【分析】根据相似三角形的判定和性质，可以求得AB的长，再根据某零件的外径为10cm，即可求得x的值．
【解答】解：∵＝＝，∠COD＝∠AOB，
∴△COD∽△AOB，
∴AB：CD＝3，
∵CD＝3cm．
∴AB＝9cm．
∵某零件的外径为10cm，
∴零件的厚度x为：（10﹣9）÷2＝0.5（cm），
故答案为：0.5．
【点评】本题考查相似三角形的应用，解答本题的关键是求出AB的值．
11．（2022秋•芦淞区期末）如图，直线y＝kx﹣2（k＞0）与双曲线在第一象限内的交点R，与x轴、y轴的交点分别为P、Q．过R作RM⊥x轴，M为垂足，若△OPQ与△PRM的面积相等，则k的值等于 2 ．
【分析】根据△OPQ与△PRM相似以及它们面积相等，可以得到两三角形全等，再根据一次函数求出点P、Q的坐标，进而得到OP、OQ的长度，再根据三角形全等表示出点R的坐标，代入反比例函数表达式，解方程即可求得k的值．
【解答】解：∵y＝kx﹣2，
∴当x＝0时，y＝﹣2，
当y＝0时，kx﹣2＝0，解得x＝，
所以点P（，0），点Q（0，﹣2），
所以OP＝，OQ＝2，
∵RM⊥x轴，
∴△OPQ∽△MPR，
∵△OPQ与△PRM的面积相等，
∴△OPQ与△PRM的相似比为1，即△OPQ≌△MPR，
∴OM＝2OP＝，RM＝OQ＝2，
所以点R（，2），
∵双曲线经过点R，
∴＝2，即k2＝8，
解得k1＝2，k2＝﹣2（舍去）．
故答案为：2．
【点评】本题综合考查了一次函数和反比例函数图象的性质，利用三角形面积相等得到两三角形全等是解本题的突破口，也是解题的关键．
12．（2022秋•丹东期末）如图，在正方形ABCD中，E为AD上的点，连接CE．以点E为圆心，以任意长为半径作弧分别交EC，ED于点N，M，再分别以M，N为圆心，以大于MN长为半径作弧，两弧在∠CED内交于点P，连接EP并延长交DC于点H，交BC的延长线于点G．若AB＝16，AE：AD＝1：4，则EH的长为 6 ．
【分析】根据题中作图判断EP是∠DEC的角平分线，利用线段比和勾股定理求出EC，再利用角平分线的性质和平行线的性质得到CG，利用相似三角形的判定和性质求出DH，最后利用勾股定理得结论．
【解答】解：∵以点E为圆心，以任意长为半径作弧分别交EC，ED于点N，M，
再分别以M，N为圆心，以大于MN长为半径作弧，两弧在∠CED内交于点P，连接EP，
∴EP是∠DEC的角平分线，
∴∠DEG＝∠CEG．
∵四边形ABCD是正方形，
∴AD＝DC＝AB＝16，∠D＝90°，AD∥BC．
∵AE：AD＝1：4，AE+ED＝16，
∴AE＝4，ED＝12．
在Rt△EDC中，
EC＝＝＝20．
∵AD∥BC，
∴∠G＝∠DEG＝∠CEG．
∴EC＝CG＝20．
∵AD∥BC，
∴△EDH∽△GCH．
∴＝＝＝．
∵DH+HC＝CD＝16，
∴DH＝6．
在Rt△EDH中，
EH＝＝＝＝6．
故答案为：6．
【点评】本题主要考查了勾股定理和相似三角形，掌握相似三角形的判定和性质、勾股定理、角平分线的作法、等腰三角形的判定等知识点是解决本题的关键．
13．（2022秋•庐阳区期末）正方形纸片ABCD中，E，F分别是AB、CB上的点，且AE＝CF，CE交AF于M．若E为AB中点，则＝ 2 ；若∠CMF＝60°，则＝ 2 ．
【分析】（1）连接BD，根据相似三角形计算即可；
（2）把60°的角放到直角三角形中，所以过C作CN⊥AM所在直线，利用角平分线的性质求解即可．
【解答】解：（1）连接BD，如图1，
∵四边形ABCD是正方形，
∴AB∥CD，且AB＝CD，
∴∠MEB＝∠MCD，∠MBE＝∠MDC，
∴△MCD∽△MEB，
∴，
∵E为AB中点，
∴；
（2）过点C作CN⊥AF，交AF的延长线于点N，如图2，
在Rt△CMN中，∠CMF＝60°，
∵sin60°＝，cs60°＝，
∴，，
即CM＝2MN，
∵AE＝CF，BA＝BC，
∴BA﹣AE＝BC﹣CF，
即BE＝BF，
∴Rt△ABF≌Rt△CBE（SAS），
∴∠FAB＝∠ECB，
∵∠AME＝∠CMF，AE＝CF，
∴△AME≌△CMF（AAS），
∴EM＝FM，
∵∠AFB＝∠CFN，∠B＝∠N＝90°
∴∠FAB＝∠FCN，
∴∠MCF＝∠NCF，
过点F作FG⊥CE于点G，
∴FG＝FN，∠FMG＝∠MCN，
∴cs∠FMG＝cs∠MCN＝，
∵，
∴，
∵＝，
MF＝EM，
∴
＝
＝2+2×
＝2+2×
＝2+．
故答案为：2；2+．
【点评】本题考查的是正方形的综合题，解题的关键是从题中找到作出正确的辅助线CN．
三．解答题（共11小题）
14．（2022秋•黄埔区期末）如图，已知AB⊥BC，EC⊥BC，垂足分别为B、C，AE交BC于点D，AB＝12，BD＝15，DC＝5，求EC的长．
【分析】根据AB⊥BC，EC⊥BC可得∠C＝∠B＝90°，由对顶角相等得∠CDE＝∠BDA，则△DCE∽△DBA，根据相似三角形的性质即可求解．
【解答】解：∵AB⊥BC，EC⊥BC，
∴∠C＝∠B＝90°，
∵∠CDE＝∠BDA，
∴△DCE∽△DBA，
∴，
∵AB＝12，BD＝15，DC＝5，
∴，
∴EC＝4．
【点评】本题主要考查相似三角形的判定与性质，熟知两个三角形相似，对应边的比相等是解题关键．
15．（2022秋•市南区期末）将一块长方体蛋糕平均分成3份，若按照如图1方式进行分割，每份的蛋糕胚一样多，但奶油不一样多（①和③奶油多，②奶油少），那么如何分割，才能使得3份的蛋糕胚和奶油一样多呢？如图2，首先我们可以将蛋糕抽象成矩形，用加粗线条表示有奶油的边，然后将矩形沿其对角线分割并拼成如图3的平行四边形ABCD，分别取边AB、CD的三等分点E、F和G、H，如图4，按EG、FH分割成3份（Ⅰ，Ⅱ，Ⅲ），此种分法能够保证每份的蛋糕坯一样多，奶油是否一样多，我们只需判断每份中加粗线条的长度和是否相等，请你给出判断并加以证明．
【分析】设BD与FH交于点M，与EG交于点N，过点N作NP∥AB交FH于点P，根据题意可得AB∥DC，BF＝CH＝EF＝GH＝AE＝DG，则Ⅰ，Ⅱ，Ⅲ区域均为平行四边形，易通过AAS证明△FBM≌△PNM，△PNM≌△GDN，得到BM＝NM＝DN，以此即可证明．
【解答】此种分法能够保证奶油一样多．
证明：设BD与FH交于点M，与EG交于点N，过点N作NP∥AB交FH于点P，如图，
∵四边形ABCD为平行四边形，E、F为AB边的三等分点，G、H为CD边三等分点，
∴AB∥DC，BF＝CH＝EF＝GH＝AE＝DG，
∴四边形FBCH、EFGH、AEGD均为平行四边形，
∵NP∥EF，EN∥FP，
∴四边形EFPN为平行四边形，∠FBM＝∠PNM，
∴NP＝EF＝BF＝DG，
在△FBM和△PNM，
，
∴△FBM≌△PNM（AAS），
∴BM＝NM，
同理可证明△PNM≌△GDN，
则NM＝DN，
∴BM＝NM＝DN，
∴AE+DG+DN＝EF+GH+NM＝BF+CH+BM，
即此种分法能够保证奶油一样多．
【点评】本题主要考查平行四边形的性质、全等三角形的判定与性质，理清题意，正确作出辅助线，熟练掌握全等三角形的判定定理是解题关键．
16．（2022秋•杭州期末）如图，在等腰三角形ABC中，AB＝AC，点D是BC的中点，点E，F分别在线段BD，AC上，连结AD，EF交于点G，∠CEF＝2∠CAD．
（1）求证：△ABC∽△EFC．
（2）若BE＝2DE，＝，求的值．
【分析】（1）根据等腰三角形的性质可得∠B＝∠C，∠CAB＝2∠CAD，根据题意不难证明△ABC∽△EFC；
（2）过点F作FH∥BC，交AD于点H，）根据等腰三角形的性质可得BD＝CD，则DE＝，易证明△AHF∽△ADC，则，易证明△HFG∽△DEG，则，将DE＝，代入即可求解．
【解答】（1）证明：∵△ABC为等腰三角形，AB＝AC，
∴∠B＝∠C，
∵点D是BC的中点，
∴∠CAB＝2∠CAD，
∵∠CEF＝2∠CAD，
∴∠CEF＝∠CAB，
在△ABC和△EFC中，
，
∴△ABC∽△EFC；
（2）过点F作FH∥BC，交AD于点H，
∵△ABC为等腰三角形，AB＝AC，点D是BC的中点，
∴BD＝CD，
∵BE＝2DE，
∴，即DE＝，
∵HF∥BC，
∴△AHF∽△ADC，
∴，
∵＝，
∴，
∴，
∵HF∥BC，
∴△HFG∽△DEG，
∴，
由上述知，DE＝，，
∴＝．
【点评】本题主要考查等腰三角形的性质、相似三角形的判定与性质，正确作出辅助线，根据相似三角形的对应边成比例答题时解题关键．
17．（2022秋•金山区校级期末）已知：如图，在△ABC中，点D在边BC上，AE∥BC，BE与AD、AC分别相交于点F、G，AF2＝FG•FE．
（1）求证：△CAD∽△CBG；
（2）联结DG，求证：DG•AE＝AB•AG．
【分析】（1）通过证明△FAG∽△FEA，可得∠FAG＝∠E，由平行线的性质可得∠E＝∠EBC＝∠FAG，且∠ACD＝∠BCG，可证△CAD∽△CBG；
（2）由相似三角形的性质可得 ＝，且∠DCG＝∠ACB，可证△CDG∽△CAB，可得 ＝，由平行线分线段成比例可得 ＝，可得结论．
【解答】证明：（1）∵AF2＝FG⋅FE．
∴＝，
∵∠AFG＝∠EFA，
∴△FAG∽△FEA，
∴∠FAG＝∠E，
∵AE∥BC，
∴∠E＝∠EBC，
∴∠EBC＝∠FAG，
∵∠ACD＝∠BCG，
∴△CAD∽△CBG；
（2）∵△CAD∽△CBG，
∴＝，
∵∠DCG＝∠ACB，
∴△CDG∽△CAB，
∴＝，
∵AE∥BC，
∴＝，
∴＝，
∴＝，
∴DG•AE＝AB•AG．
【点评】本题考查了相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．
18．（2022秋•文山市期末）如图，在四边形ABCD中，对角线AC、BD相交于点E，DB平分∠ADC，且AB2＝BE•BD．求证：△ABE∽△DCE．
【分析】根据相似三角形的判定可得△ABE∽△DBA；所以∠BAC＝∠BDC，由此可得出△ABE∽△DCE．
【解答】证明：∵AB2＝BE•BD，
∴AB：BE＝BD：AB，
∵∠ABE＝∠DBA，
∴△ABE∽△DBA，
∴∠BAC＝∠BDC，
∵BD平分∠ADC，
∴∠ADB＝∠BDC＝∠BAC，
∴△ABE∽△DCE．
【点评】本题主要考查相似三角形的判定，涉及A字型相似，8字型相似等相关内容，熟练掌握相关判定是解题关键．
19．（2022秋•阳谷县期末）如图，在四边形ABCD中，对角线AC与BD交于点E，DB平分∠ADC，且AB2＝BE•BD．
（1）求证：△ABE∽△DCE；
（2）AE•CD＝BC•ED．
【分析】（1）根据相似三角形的判定可得△ABE∽△DBA；所以∠BAC＝∠BDC，由此可得出△ABE∽△DCE；
（2）由（1）中的相似可得出AE：DE＝BE：CE，再由∠BEC＝∠AED可得△ADE∽△BCE，所以∠EAD＝∠EBC，∠ADE＝∠BDC＝∠BCE，可得△BCD∽△ADE，进而可得结论．
【解答】证明：（1）∵AB2＝BE•BD，
∴AB：BE＝BD：AB，
∵∠ABE＝∠DBA，
∴△ABE∽△DBA，
∴∠BAC＝∠BDC，
∵BD平分∠ADC，
∴∠ADB＝∠BDC＝∠BAC，
∴△ABE∽△DCE；
（2）由（1）中相似可得，AE：DE＝BE：CE，
∵∠BEC＝∠AED，
∴△ADE∽△BCE，
∴∠EAD＝∠EBC，∠ADE＝∠BDC＝∠BCE，
∴△BCD∽△AED，
∴BC：AE＝CD：ED，
AE•CD＝BC•ED．
【点评】本题主要考查相似三角形的性质与安定，涉及A字型相似，8字型相似等相关内容，熟练掌握相关判定是解题关键．
20．（2022秋•吉州区期末）如图，BD、AC相交于点P，连接BC、AD，且∠1＝∠2，若PB＝3，PC＝1，PD＝2，求PA的长度．
【分析】根据8字型模型证明两个三角形相似即可解答．
【解答】解：∵∠1＝∠2，∠APD＝∠BPC，
∴△DAP∽△CBP，
∴＝，
∴＝，
∴AP＝6．
【点评】本题考查了相似三角形的判定与性质，熟练掌握8字型模型相似三角形是解题的关键．
21．（2022秋•平谷区期末）如图，已知锐角∠ABC，以AB为直径画⊙O，交BC边于点M，BD平分∠ABC与⊙O交于点D，过点D作DE⊥BC于点E．
（1）求证：DE是⊙O的切线；
（2）连接OE交BD于点F，若∠ABC＝60°，AB＝4，求DF长．
【分析】（1）连接OD，根据OD＝OB得到∠ODB＝∠OBD，再根据角平分线的性质得∠OBD＝∠DBE，以此得到OD∥BE，从而即可证明；
（2）连接AD，OD，可得∠ADB＝90°，根据∠ABC＝60°得到AD＝2，再根据勾股定理即可以此求出BD＝，BE＝3，由（1）知，OD∥BE，则△DFO∽△BFE，根据相似三角形的性质得到，即，最后由即可求出DF的长．
【解答】（1）证明：如图，连接OD，
则OD＝OB，
∴∠ODB＝∠OBD，
∵BD平分∠ABC，
∴∠OBD＝∠DBE，
∴∠ODB＝∠DBE，
∴OD∥BE，
∵DE⊥BC，
∴∠DEB＝∠EDO＝90°，
∵OD为半径，
∴DE是⊙O的切线；
（2）解：如图，连接AD，OD，
∵AB为直径，
∴∠ADB＝90°，
∵∠ABC＝60°，AB＝4，
∴∠ABD＝∠DBE＝30°，OD＝OB＝2，
∴AD＝2，
在Rt△ADB中，＝，
∴DE＝，
在Rt△DEB中，＝3，
∵OD∥BE，
∴△DFO∽△BFE，
∴，即，
∵，
∴DF+，
解得：DF＝．
【点评】本题考查了切线的判定与性质，相似三角形的判定与性质，圆周角定理，勾股定理，角平分线的性质，解含30度角的直角三角形，熟练掌握相关知识是解题关键．
22．（2022秋•辛集市期末）以下各图均是由边长为1的小正方形组成的网格，A，B，C，D均在格点上．
（1）在图①中，的值为 1：3 ；
（2）利用网格和无刻度的直尺作图，保留痕迹，不写作法．
①如图②，在AB上找一点P，使AP＝3；
②如图③，在BD上找一点P，使△APB∽△CPD．
【分析】（1）如图①中，利用平行线的性质求解即可．
（2）①根据勾股定理得AB的长为5，再根据相似三角形的判定方法即可找到点P；
②作点A的对称点A′，连接A′C与BD的交点即为要找的点P，使△APB∽△CPD．
【解答】解：（1）如图①中，
∵AB∥CD，
∴△PCD∽△PBA．
∴＝＝，
故答案为：1：3；
（2）
①取格点E，F，连接EF交AB于点P，点P即为所求的点．
由勾股定理知：AB＝＝5．
∵AP＝3，
∴BP＝2．
∵BE∥FA，
∴△EPB∽△FPA．
∵AP：BP＝AF：BE＝3：2．
∴取格点E，F，连接EF交AB于点P，点P即为所求的点；
②如图③所示，作点A的对称点A′，
连接A′C，交BD于点P，
点P即为所要找的点，
∵AB∥CD，
∴△APB∽△CPD．
【点评】本题属于相似综合题，主要考查作图﹣应用与设计，相似三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
23．（2022秋•双流区期末）小明为了测量出一深坑的深度，采取如下方案：如图，在深坑左侧用观测仪AB从观测出发点A观测深坑底部P，且观测视线刚好经过深坑边缘点E，在深坑右侧用观测仪CD从测出发点C观测深坑底部P，且观测视线恰好经过深坑边缘点F，点B，E，F，D在同一水平线上．已知AB⊥EF，CD⊥EF，观测仪AB高2m，观测仪CD高1m，BE＝1.6m，FD＝0.8m，深坑宽度EF＝8.8m，请根据以上数据计算深坑深度多少米？
【分析】过点P作PH垂直EF，垂足为H，然后根据已知证明△ABM∽△PHM，△CDN∽△PHN，得出HP＝＝，设MH＝x m，则NH＝（8.8﹣x）m，解得MH＝4.4，再求HP即可．
【解答】解：过点P作PH垂直EF，垂足为H，如图：
∵AB⊥EF，PH⊥EF，CD⊥EF，
∴AB∥HP，CD∥HP，
∴△ABM∽△PHM，△CDN∽△PHN，
∴＝，＝，
∴HP＝，HP＝，
∴＝，
∵AB＝2m，BM＝1.6m，CD＝1m，DN＝0.8m，MN＝8.8m，
设MH＝x m，则NH＝（8.8﹣x）m，
∴＝，
∴x＝4.4，
∴HP＝＝＝5.5（m），
∴深坑深度5.5米．
【点评】本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
24．（2022秋•南开区校级期末）如图，在▱ABCD中，G是CD延长线上一点，连接BG交AC，AD于E，F．
（1）求证：△ABE∽△CGE；
（2）若AF＝2FD，求的值．
【分析】（1）根据平行四边形对边平行，得到∠ABE＝∠CGE，再利用对顶角相等，可得△ABE∽△CGE；
（2）利用平行四边形对边平行，证明△AEF∽△CEB，得到，再由（1）得，，从而求解．
【解答】（1）证明：∵四边形ABCD为平行四边形，
∴AB∥CD，
∴∠ABE＝∠CGE，
又∵∠AEB＝∠CGE，
∴△ABE∽△CGE．
（2）解：设FD＝m，则AF＝2m，
∴AD＝3m，
∵四边形ABCD为平行四边形，
∴AD∥BC，BC＝AD＝3m，
∴∠EAF＝∠ECB，∠AFE＝∠CBE，
∴△AEF∽△CEB
∴＝＝，
又∵△ABE∽△CGE，
∴＝＝．
即 的值为．
【点评】本题考查了相似三角形的性质与判定，熟练运用相似三角形的判定与性质是解题的关键．
题型二：“A”字模型相似三角形
一．选择题（共4小题）
1．（2023春•东平县期末）如图，P为△ABC的边AB上一点（AB＞AC），则下列条件不一定能保证△ABC∽△ACP的是（ ）
A．∠ACP＝∠BB．∠APC＝∠ACBC．D．
【分析】对于选项A，可考虑判定“两角对应相等，两三角形相似”；
对于选项B，可考虑判定“两角对应相等，两三角形相似”；
对于选项C，可考虑判定“两边对应成比例且夹角相等，两三角形相似”；
对于选项D，可考虑判定“两边对应成比例且夹角相等，两三角形相似”或“三边对应成比例，两三角形相似”．
【解答】解：对于选项A，∠ACP＝∠B，因为∠CAP＝∠BAC，所以△ABC∽△ACP（两角对应相等，两三角形相似），故A不符合题意；
对于选项B，∠APC＝∠ACB，因为∠CAP＝∠BAC，所以△ABC∽△ACP（两角对应相等，两三角形相似），故B不符合题意；
对于选项C，，因为∠CAP＝∠BAC，所以△ABC∽△ACP（两边对应成比例且夹角相等，两三角形相似），故C不符合题意；
对于选项D，，因为∠PCA不一定等于∠CBA，或不一定等于，所以不一定能保证△ABC∽△ACP，故D符合题意．
故选：D．
【点评】本题考查了三角形相似的两个判定：两角对应相等两三角形相似；两边对应成比例且夹角相等，两三角形相似．关键是找到对应角和边．
2．（2023春•海东市期末）如图，在边长为6的正方形ABCD中，E为CD上的点，F为BC的中点，连接AE，AF，点M，N分别是AE和AF的中点，若DE＝2，则MN的长为（ ）
A．B．2C．D．3
【分析】依据点M，N分别是AE和AF的中点，即可得到MN是△AEF的中位线，故MN的长即为EF的长的一半；在Rt△CEF中根据勾股定理求得EF的长，即可得出结论．
【解答】解：∵在边长为6的正方形ABCD中，DE＝2，F为BC的中点，
∴CF＝3，CE＝4，
∴Rt△CEF中，EF＝＝5．
∵点M，N分别是AE和AF的中点，
∴MN是△AEF的中位线，
∴MN＝EF＝＝，
故选：C．
【点评】本题主要考查了三角形中位线定理以及勾股定理的运用，关键是掌握：三角形的中位线平行于第三边，并且等于第三边的一半．
3．（2023春•芝罘区期末）操场上有一根竖直的旗杆AB，它的一部分影子（BC）落在水平地面上，另一部分影子（CD）落在操场的墙壁上，经测量，墙壁上的影高为1.2m，地面的影长为2.6m，同时测得一根高为2m的竹竿OM的影长是ON＝1.6m，请根据以上信息，则旗杆的高度是（ ）
A．3.25mB．4.25mC．4.45mD．4.75m
【分析】首先需先求出这棵树全落在地面上时的影子的长，即这棵树在底面上的影子长与墙壁上的影子落在地面上的投影长度之和；一根长为2m的竹竿的影长是1.6m；根据竹竿的高与其影长的比值和树高与其影长的比值相同，即可列方程求出这棵树的高度．
【解答】解：由题意可知，留在墙壁上的树影高为1.2m，
设这段影子在地面上的长为a，可得：
＝，
∴a＝0.96m．
∴这棵树全落在地面上时的影子的长为：2.6+0.96＝3.56（m）．
设树高为x m，再根据竹竿的高与其影长的比值和树高与其影长的比值相同可列比例式为：
＝，
∴x＝4.45．
∴树高是4.45m．
故选：C．
【点评】本题考查了相似三角形的应用，根据相似三角形对应边成比例列方程是解题的关键．
4．（2023春•环翠区期末）如图，在▱ABCD中，点E在对角线BD上，EM∥AD，交AB于点M，EN∥AB，交AD于点N，则下列式子一定正确的是（ ）
A．B．C．D．
【分析】利用平行线分线段成比例定理和相似三角形的性质逐个判断得结论．
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC．
A．∵EM∥AD，
∴＝．
∵EN∥AB，
∴△DNE∽△EMB．
∴＝．
∵DE不一定等于BM，
∴＝不一定成立，故选项A不一定正确；
B．∵EM∥AD，
∴＝．
∵EN∥AB，
∴
∵DE不一定等于BE，
∵不一定成立，故选项B不一定正确；
C．∵EM∥AD，
∴△BEM∽△BDA．
∴＝，故选项C一定正确；
D．由C可得，故选项D一定不正确．
故选：C．
【点评】本题主要考查了相似三角形的性质，掌握平行线分线段成比例定理、相似三角形的判定和性质是解决本题的关键．
二．填空题（共5小题）
5．（2023春•八步区期末）如图，在△ABC中，D，E分别为AB，AC的中点，F是AD的中点，FG∥DE，若BC+FG＝15，则DE的长为 6 ．
【分析】首先利用三角形中位线定理推出DE平行且等于BC，再根据“A”字模型证明三角形相似，进而得到FG＝BC，然后利用BC+FG＝15，求出BC的长，进而求解．
【解答】解：∵D，E分别为AB，AC的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE＝BC，
∵FG∥DE，
∴FG∥DE∥BC，
∴△AFG∽△ABC，
又∵F是AD的中点，D是AB的中点，
∴，
∴FG＝BC，
∵BC+FG＝15，
∴BC+BC＝15，
∴BC＝12，
∴DE＝×12＝6．
故答案为：6．
【点评】本题考查了相似三角形的性质和判定，三角形中位线定理，解题关键是根据相似三角形的性质求出FG与BC的数量关系．
6．（2023春•南关区校级期末）明珠绿星数学社团想利用标杆测量楼高，小明先在N处竖立一根高1.6m的标杆MN，发现点B、M、P在同一直线上．测得PN＝0.5m，AN＝4.5m，已知，点A、N、P在同一直线上，MN⊥AP于点N，AB⊥AP于点A．则楼高AB为 16 m．
【分析】根据垂直定义可得∠BAP＝∠MNP＝90°，然后证明△BAP∽△MNP，从而利用相似三角形的性质进行计算，即可解答．
【解答】解：∵MN⊥AP，AB⊥AP，
∴∠BAP＝∠MNP＝90°，
∵∠P＝∠P，
∴△BAP∽△MNP，
∴＝，
∴＝，
解得：AB＝16，
∴楼高AB为16m，
故答案为：16．
【点评】本题考查了相似三角形的应用，熟练掌握A字模型相似三角形是解题的关键．
7．（2023春•重庆期末）如图，小明站在两路灯AB、CD之间的点F处，两路灯底部的距离BD＝10m，两路灯的高度均为8m，小明身高EF＝1.6m，他在路灯AB下的影子FM＝1m，在路灯CD下的影子为FN，则FN＝ ．
【分析】根据题意可得：EF⊥BD，AB⊥BD，CD⊥BD，从而可得∠B＝∠EFM＝∠EFN＝∠D＝90°，然后先证明A字模型相似三角形△EFM∽△ABM，从而利用相似三角形的性质求出BM的长，进而求出DM的长，最后再证明A字模型相似三角形△NFE∽△NDC，从而利用相似三角形的性质进行计算，即可解答．
【解答】解：由题意得：EF⊥BD，AB⊥BD，CD⊥BD，
∴∠B＝∠EFM＝∠EFN＝∠D＝90°，
∵∠EMF＝∠AMB，
∴△EFM∽△ABM，
∴＝，
∴＝，
解得：BM＝5m，
∵BD＝10m，
∴DM＝BD﹣BM＝5（m），
∵∠ENF＝∠CND，
∴△NFE∽△NDC，
∴＝，
∴＝，
解得：NF＝m，
故答案为：．
【点评】本题考查了相似三角形的应用，中心投影，熟练掌握A字模型相似三角形是解题的关键．
8．（2023春•虹口区期末）如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，点D是AB的中点．将△ADC绕点A旋转得到△AD1C1（点D与点D1对应，点C与点C1对应），当点C1落在边AB上时，联结BD1，那么线段BD1的长是 3 ．
【分析】延长D1C1交BC于点E，在Rt△ABC中，利用勾股定理可得AB＝10，再利用直角三角形斜边上的中线性质可得AD＝CD＝5，从而可得∠DAC＝∠DCA，然后根据旋转的性质可得：D1C1＝CD＝5，AC＝AC1＝8，∠ACD＝∠AC1D1，从而可得BC1＝2，∠DAC＝∠D1C1A，进而可得DE∥AC，再利用平行线的性质可得∠BEC1＝∠BCA＝90°，∠BC1E＝∠BAC，从而可得△BC1E∽△BAC，最后利用相似三角形的性质可得C1E＝1.6，BE＝1.2，从而可得D1E＝6.6，再在Rt△D1EB中，利用勾股定理进行计算即可解答．
【解答】解：延长D1C1交BC于点E，
∵∠ACB＝90°，AC＝8，BC＝6，
∴AB＝＝＝10，
∵点D是AB的中点，
∴AD＝CD＝AB＝5，
∴∠DAC＝∠DCA，
由旋转得：D1C1＝CD＝5，AC＝AC1＝8，∠ACD＝∠AC1D1，
∴BC1＝AB﹣AC1＝10﹣8＝2，∠DAC＝∠D1C1A，
∴DE∥AC，
∴∠BEC1＝∠BCA＝90°，∠BC1E＝∠BAC，
∴△BC1E∽△BAC，
∴＝＝，
∴＝＝，
∴C1E＝1.6，BE＝1.2，
∴D1E＝D1C1+C1E＝5+1.6＝6.6，
在Rt△D1EB中，BD1＝＝＝3，
故答案为：3．
【点评】本题考查了旋转的性质，相似三角形的判定与性质，勾股定理，直角三角形斜边上的中线，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
9．（2022秋•阳曲县期末）已知：如图，在△ABC中，AC＝6，BC＝8，AB＝10，点D位于边AB上，过点D作边BC的平行线交边AC于点E，过点D作边AC的平行线交边BC于点F，设AE＝x，四边形CEDF的面积为y，则y关于x的函数关系式是 y＝﹣x2+8x ．（不必写定义域）
【分析】根据已知可证四边形DECF是平行四边形，然后利用勾股定理的逆定理证明△ABC是直角三角形，从而可得∠C＝90°，进而可得四边形DECF是矩形，再证明A字模型相似三角形△AED∽△ABC，从而利用相似三角形的性质可得DE＝x，最后根据矩形的面积公式进行计算即可解答．
【解答】解：∵DE∥BC，DF∥AC，
∴四边形DECF是平行四边形，
在△ABC中，AC＝6，BC＝8，AB＝10，
∵AC2+BC2＝62+82＝100，AB2＝102＝100，
∴AC2+BC2＝AB2，
∴△ABC是直角三角形，
∴∠C＝90°，
∴四边形DECF是矩形，
∵DE∥BC，
∴∠AED＝∠C＝90°，
∵∠A＝∠A，
∴△AED∽△ABC，
∴＝，
∴＝，
∴DE＝x，
∴矩形CEDF的面积＝DE•CE，
∴y＝x（6﹣x）＝﹣x2+8x，
故答案为：y＝﹣x2+8x．
【点评】本题考查了相似三角形的判定与性质，勾股定理的逆定理，函数关系式，熟练掌握A字模型相似三角形是解题的关键．
三．解答题（共7小题）
10．（2023春•龙口市期末）下表是小明填写的实践活动报告的部分内容，请你借助小明的测量数据，计算小河的宽度．
【分析】根据题意可得：CB⊥AB，ED⊥AD，从而可得∠CBA＝∠EDA＝90°，然后证明A字模型相似三角形△ABC∽△ADE，从而利用相似三角形的性质进行计算，即可解答．
【解答】解：由题意得：CB⊥AB，ED⊥AD，
∴∠CBA＝∠EDA＝90°，
∵∠CAB＝∠EAD，
∴△ABC∽△ADE，
∴，
∴，
解得：AB＝12，
∴小河的宽度为12m．
【点评】本题考查了相似三角形的应用，熟练掌握A字模型相似三角形是解题的关键．
11．（2023春•广州期末）如图，在△ABC中，AD⊥BC于点D，AD＝2，BD＝1，DC＝4，求∠BAC的度数．
【分析】此题类似于射影定理模型，想到三角形相似．
【解答】解：∵AD＝2，BD＝1，DC＝4，
∴，
∵∠BDA＝∠ADC＝90°，
∴△BDA∽△ADC，
∴∠BAD＝∠C，
∵∠C+∠DAC＝90°，
∴∠BAD+∠DAC＝90°，
∴∠BAC＝90°．
【点评】本题考查了相似三角形的判断：夹角相等，对应边成比例．从条件AD＝2，BD＝1，DC＝4上联想成比例．
12．（2022秋•峄城区期末）已知△ABC中，∠ACB＝90°，AC＝BC＝4cm，点P从点A出发，沿AB方向以每秒cm的速度向终点B运动，同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，设运动的时间为t秒．
（1）如图①，若PQ⊥BC，求t的值；
（2）如图②，将△PQC沿BC翻折至△P′QC，当t为何值时，四边形QPCP′为菱形？
【分析】（1）根据勾股定理求出AB，根据相似三角形的性质列出比例式，计算即可．
（2）作PD⊥BC于D，PE⊥AC于E，AP＝t cm，BQ＝t cm（0≤t＜4），由△ABC为等腰直角三角形，可得∠A＝∠B＝45°，则可判断△APE和△PBD为等腰直角三角形，得出PE＝AE＝AP＝t cm，BD＝PD，则CE＝AC﹣AE＝（4﹣t）cm，由矩形和菱形性质及勾股定理，即可求得答案．
【解答】解：（1）如图①，∵∠ACB＝90°，AC＝BC＝4cm，
∴AB＝＝＝4（cm），
由题意得，AP＝t cm，BQ＝t cm，
则BP＝（4﹣t）cm，
∵PQ⊥BC，
∴∠PQB＝90°，
∴∠PQB＝∠ACB，
∴PQ∥AC，
∴＝，
∴＝，
解得：t＝2，
∴当t＝2时，PQ⊥BC．
（2）作PD⊥BC于D，PE⊥AC于E，如图②，
AP＝t cm，BQ＝t cm（0≤t＜4），
∵∠C＝90°，AC＝BC＝4cm，
∴△ABC为等腰直角三角形，
∴∠A＝∠B＝45°，
∴△APE和△PBD为等腰直角三角形，
∴PE＝AE＝AP＝t cm，BD＝PD，
∴CE＝AC﹣AE＝（4﹣t）cm，
∵四边形PECD为矩形，
∴PD＝EC＝（4﹣t）cm，
∴BD＝（4﹣t）cm，
∴QD＝BD﹣BQ＝（4﹣2t）cm，
在Rt△PCE中，PC2＝PE2+CE2＝t2+（4﹣t）2，
在Rt△PDQ中，PQ2＝PD2+DQ2＝（4﹣t）2+（4﹣2t）2，
∵四边形QPCP′为菱形，
∴PQ＝PC，
∴t2+（4﹣t）2＝（4﹣t）2+（4﹣2t）2，
∴t1＝，t2＝4（舍去）．
∴当t的值为时，四边形QPCP′为菱形．
【点评】此题是相似形综合题，主要考查的是菱形的性质、等腰直角三角形的性质，线段垂直平分线的性质，用方程的思想解决问题是解本题的关键．
13．（2023春•牟平区期末）我国古代数学家赵爽利用影子对物体进行测量的方法，在至今仍有借鉴意义．如图所示，现将一高为2米的木杆CG放在灯杆AB前，测得其影长CH为1米，再将木杆沿着BC方向移动1.8米至DE的位置（CG＝DE），此时测得其影长DF为3米，求灯杆AB的高度．
【分析】根据题意可得：CD＝1.8米，AB⊥BF，GC⊥BF，ED⊥BF，从而可得∠B＝∠GCH＝∠EDF＝90°，然后证明A字模型相似三角形GCH∽△ABH，△EDF∽△ABF，从而利用相似三角形的性质进行计算，即可解答．
【解答】解：由题意得：CD＝1.8米，AB⊥BF，GC⊥BF，ED⊥BF，
∴∠B＝∠GCH＝∠EDF＝90°，
∵∠GHC＝∠AHB，
∴△GCH∽△ABH，
∴＝，
∴＝，
∵∠F＝∠F，
∴△EDF∽△ABF，
∴＝，
∴＝，
∴＝，
解得：BC＝0.9，
∴＝，
解得：AB＝3.8，
∴灯杆AB的高度为3.8米．
【点评】本题考查了相似三角形的应用，中心投影，平移的性质，数学常识，熟练掌握相似三角形的判定与性质是解题的关键．
14．（2023春•振兴区校级期末）综合与实践
问题情境：数学活动课上，王老师出示了一个问题：
如图1，AB＝BC，AD＝DE，∠ABC＝∠ADE＝α，连接BD、CE．当α＝60°时，通过测量，猜想出图中与BD相等的线段，并加以证明．
独立思考：（1）请解答王老师提出的问题．
实践探究：（2）王老师修改条件，并提出新问题，请你解答．
如图2，AB＝BC，AD＝DE，∠ABC＝∠ADE＝α，连接BD、CE．当α＝120°时，请用已学的知识求出的值．
【分析】（1）α＝60°时，三角形ABC和三角形ADE都是等边三角形，可得AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，进而证明三角形ABD全等于三角形ACE可得结论；
（2）根据AB＝BC，AD＝DE，∠ABC＝∠ADE＝α＝120°，可证明△ABD∽△ACE，又△ABC中∠BAC＝120°，AB＝AC，则AC＝AB，根据相似三角形的性质可得结论．
【解答】（1）证明：∵∠BAC＝∠DAE＝60°，
∴∠BAC+∠DAC＝∠DAE+∠DAC，
∴∠BAD＝∠CAE，
在△BAD与△CAE中，
，
∴△BAD≌△CAE（SAS），
∴BD＝CE；
（2）作BM⊥AC于M点，
∵AB＝BC，∠ABC＝120°，
∴AC＝2AM，∠BAC＝30°，
∴AB＝2BM，
在Rt△ABM中，由勾股定理得：
AB2＝BM2+AM2
∴4BM2＝BM2+AM2，
解得：AM＝BM，
∴，
∵DA＝AE，∠DAE＝120°，
∴∠DAE＝30°，
∵∠BAC＝∠DAE＝120°，
∴△BAD∽△CAE，
∴．
【点评】本题考查了全等三角形的判定和性质，以及相似三角形的判定和性质，等腰三角形的性质．
15．（2023春•德化县期末）如图，将线段AB平移得到CD，使A与D对应，B与C对应，连接AD，BC．
（1）求证：∠B＝∠ADC；
（2）点G在BC的延长线上，点C与C′关于直线DG对称，直线DC′交BC的延长线于点E．点F在线段CE上，且∠DFE＝∠EDF．
①设∠B＝α，求∠FDG的度数（用含α的代数式表示）；
②证明：．
【分析】（1）根据平移的性质可得AB∥CD，AB＝CD，从而可得四边形ABCD是平行四边形，然后利用平行四边形的性质即可解答；
（2）①利用平行线的性质可得∠B＝∠DCF＝α，再根据三角形的外角性质可得∠DFE＝∠DCF+∠CDF，从而利用角的和差关系可得∠CDE＝2∠CDF+∠DCF，然后根据轴对称的性质可得∠CDG＝∠C′DG＝∠CDE＝∠CDF+∠DCF，从而可得∠CDG﹣∠CDF＝∠DCF，进而可得∠FDG＝∠DCF＝α，即可解答；
②过点G作GH∥CD，交DE于点H，连接GC′，先证明A字模型相似三角形△CDE∽△GHE，从而可得＝，再根据轴对称的性质可得△CDG≌△C′DG，从而可得CG＝C′G，∠DCG＝∠DC′G，进而可得∠DC′G＝∠HGE，然后证明△HC′G∽△HGE，从而利用相似三角形的性质可得＝，即可解答．
【解答】（1）证明：由平移得：AB∥CD，AB＝CD，
∴四边形ABCD是平行四边形，
∴∠B＝∠ADC；
（2）①解：∵AB∥CD，
∴∠B＝∠DCF＝α，
∵∠DFE是△DCF的一个外角，
∴∠DFE＝∠DCF+∠CDF，
∵∠DFE＝∠EDF，
∴∠CDE＝∠CDF+∠EDF
＝∠CDF+∠DFE
＝∠CDF+∠DCF+∠CDF
＝2∠CDF+∠DCF，
∵点C与C′关于直线DG对称，
∴∠CDG＝∠C′DG＝∠CDE＝（2∠CDF+∠DCF）＝∠CDF+∠DCF，
∴∠CDG﹣∠CDF＝∠DCF，
∴∠FDG＝∠DCF＝α，
∴∠FDG的度数为α；
②过点G作GH∥CD，交DE于点H，连接GC′，
∴∠DCG＝∠HGE，∠CDH＝∠GHE，
∴△CDE∽△GHE，
∴＝，
∵点C与C′关于直线DG对称，
∴△CDG≌△C′DG，
∴CG＝C′G，∠DCG＝∠DC′G，
∴∠DC′G＝∠HGE，
∵∠GHE＝∠GHC′，
∴△HC′G∽△HGE，
∴＝，
∴＝，
∴＝．
【点评】本题考查了相似三角形的判定与性质，平行四边形的判定与性质，轴对称的性质，平移的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
16．（2022秋•大连期末）如图，在Rt△ABC中，∠ACB＝90°，AC＝8cm，BC＝6cm．D为AC中点，过D作DE⊥AC交AB于点E．动点P从点D出发，沿射线DE以1cm/s的速度运动．过D作DM∥AB，过P作PM⊥DM于点M．设点P的运动时间为t（s）．△PDM与△ABC重叠部分图形的面积为S（cm2）．
（1）当点M落在BC边上时，求t的值；
（2）当点M在△ABC内部时，求S关于t的函数解析式，并直接写出自变量t的取值范围．
【分析】（1）根据题意可得AB＝10cm，DM＝5cm，再根据DM∥AB，PM⊥DM可得∠PDM＝∠B，∠PMD＝∠ACB＝90°，从而可证△PDM∽△ABC，根据相似三角形的性质可得PD＝cm，以此即可求解；
（2）当点M在△ABC内部时，在（1）的情况下，达到了最大值，①当0＜t≤3时，S＝S△PDM，此时PD＝t，由△PDM∽△ABC可得PM＝，DM＝，以此即可算出S；②当3＜t≤时，过E作EQ⊥DM交DM于点Q，S＝S四边形EDMN＝S△EDQ+S四边形ENMQ，根据题意可得DE＝3，四边形ENMQ为矩形，再由△DQE∽△BCA得DQ＝，QE＝，，根据△PEN∽△EDQ得EN＝，以此即可算出S．
【解答】解：（1）如图，此时点M落在BC边上，
∵∠ACB＝90°，AC＝8cm，BC＝6cm，
∴cm，
∵D为AC中点，DM∥AB，
∴cm，
∵DE⊥AC，
∴∠PDC＝90°，
∵DM∥AB，
∴∠A＝∠MDC，
∵∠A+∠B＝90°，∠PDM+∠MDC＝90°，
∴∠PDM＝∠B，
∵PM⊥DM，
∴∠PMD＝∠ACB＝90°，
∴△PDM∽△ABC，
∴，即，
∴PD＝cm，
∴t＝（s），
∴当点M落在BC边上时，t的值为；
（2）由（1）可知，当点M在△ABC内部时，在（1）的情况下，达到了最大值，
当点P位于点D位置时，达到了最小值，
①当0＜t≤3时，S＝S△PDM，
此时PD＝t，
根据△PDM∽△ABC，可得，
即，
∴PM＝，DM＝，
∴，
∴；
②当3＜t≤时，如图，过E作EQ⊥DM交DM于点Q，
S＝S四边形EDMN＝S△EDQ+S四边形ENMQ，
∵D为AC中点，DE⊥AC，
∴DE∥BC，
∴，
∵EQ⊥DM，PM⊥DM，
∴EQ∥PM，四边形ENMQ为矩形，
∴△DQE∽△DMP，
∴△DQE∽△BCA，
∴，即，
∴DQ＝，QE＝，
∴，
此时，PD＝t，PE＝t﹣3，
∵DM∥AB，
∴△PEN∽△EDQ，
∴，即，
∴EN＝，
∴＝，
∴S＝S四边形EDMN＝S△EDQ+S四边形ENMQ＝，
综上，当0＜t≤3时，；当3＜t≤时，．
【点评】本题主要考查相似三角形的判定与性质，三角形的中位线，三角形的面积以及矩形的面积，熟练掌握相似三角形的性质，运用分类讨论思想是解题关键．
题型三：一线三等角构造相似模型
一．选择题（共3小题）
1．（2023春•荣昌区期末）如图，在矩形ABCD中，AB＝6，将点B折叠到CD边上点E处，折痕为AF，连接AE，EF，若点E是CD中点，则CF长为（ ）
A．B．1C．2D．3
【分析】依据矩形的性质以及折叠，即可得到AD，DE，CE的长；再根据△ADE∽△EFC，利用对应边成比例即可得CF的长．
【解答】解：∵矩形ABCD中，AB＝6，
∴CD＝6，
又∵E是CD的中点，
∴DE＝CE＝3，
Rt△ADE中，AD＝＝3，
由题可得，∠D＝∠C＝∠AEF＝90°，
∴∠AED+∠CEF＝90°＝∠EFC+∠CEF，
∴∠AED＝∠EFC，
∴△ADE∽△EFC，
∴＝，即＝，
解得CF＝，
故选：A．
【点评】本题主要考查了折叠问题、矩形的性质、相似三角形的性质以及勾股定理的运用，翻折变换（折叠问题）实质上就是轴对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
2．（2022秋•宁德期末）如图，在边长为4的等边△ABC中，点D是AB边上一个动点，沿过点D的直线折叠∠A，使点A落在BC边上的点F处，折痕交AC于点E，当BF＝1，AE＝时，则AD的长是（ ）
A．B．C．2D．
【分析】首先由翻折性质得到△ADE≌△DEF，所以AD＝DF，AE＝EF，再利用一线三等角证明出△BDF∽△CEF，最后根据相似三角形对应边的比相等计算出DF的长即可解答．
【解答】解：∵△ABC边长为4，AE＝，
∴CE＝4﹣＝，
∵由翻折性质得：△ADE≌△FDE，
∴AD＝DF，AE＝EF，
∵∠DFE＝∠A＝60°，
∴∠DFB+∠EFC＝120°，
∵∠C＝60°，
∴∠EFC+∠CEF＝120°，
∴∠CEF＝∠DFB，
∵∠B＝∠C＝60°，
∴△BDF∽△CFE，
∴BD：CF＝BF：CE＝DF：FE＝1：，
∴DF＝FE＝，
∴AD＝DF＝．
故选：B．
【点评】本题重点考查了折叠的两个图形全等、全等三角形的性质、相似三角形的判定与性质，解题关键是利用一线三等角证明三角形相似．
3．（2022秋•邹城市校级期末）如图，AB⊥BD于点B，ED⊥BD于点D．AB＝2，DE＝4，BD＝6．点C为BD上一点，连接AC、CE．当BC＝（ ）时，可使AC⊥CE．
A．3B．2或4C．D．2或3
【分析】根据垂直定义可得∠B＝∠D＝∠ACE＝90°，从而利用直角三角形的两个锐角互余可得∠A+∠ACB＝90°，再利用平角定义可得∠ACB+∠ECD＝90°，然后利用同角的余角相等可得∠ECD＝∠A，从而证明△ABC∽△CDE，最后利用相似三角形的性质进行计算即可解答．
【解答】解：∵AB⊥BD，ED⊥BD，
∴∠B＝∠D＝90°，
∴∠A+∠ACB＝90°，
∵AC⊥CE，
∴∠ACE＝90°，
∴∠ACB+∠ECD＝180°﹣∠ACE＝90°，
∴∠ECD＝∠A，
∴△ABC∽△CDE，
∴＝，
∴＝，
解得：BC＝2或BC＝4，
∴当BC＝2或4时，可使AC⊥CE，
故选：B．
【点评】本题考查了相似三角形的判定与性质，熟练掌握一线三等角构造相似模型是解题的关键．
二．填空题（共5小题）
4．（2023春•宁波期末）如图，在矩形ABCD中AB＝7cm、BC＝8cm，现将矩形沿EF折叠，点C翻折后交AB于点G，点D的对应点为点H，当BG＝4cm时，线段GI的长为 5 cm．
【分析】设BE＝x，则CE＝8﹣x＝GE，Rt△BGE中利用勾股定理即可得到BE的长，进而得出GE的长．再根据△AIG∽△BGE，利用对应边成比例即可得到GI的长．
【解答】解：设BE＝x，则CE＝8﹣x＝GE，
Rt△BGE中，BE2+BG2＝GE2，
∴x2+42＝（8﹣x）2，
解得x＝3，
∴BE＝3，GE＝5，
由题可得，∠A＝∠B＝∠EGI＝90°，AG＝7﹣4＝3，
∴∠AGI+∠BGE＝90°＝∠BEG+∠BGE，
∴∠AGI＝∠BEG，
∴△AIG∽△BGE，
∴＝，即＝，
解得GI＝5，
故答案为：5．
【点评】本题主要考查了矩形的性质、勾股定理以及相似三角形的判定与性质的运用，解决问题的关键是利用一线三等角构造相似模型．
5．（2022秋•武功县期末）如图，四边形ABCD是正方形，AB＝6，E是BC中点，连接DE，DE的垂直平分线分别交AB、DE、CD于M、O、N，连接EN，过E作EF⊥EN交AB于F，则AF＝ 2 ．
【分析】设CN＝x，则DN＝6﹣x，利用线段垂直平分线性质可得EN＝DN＝6﹣x，运用勾股定理建立方程求解即可求得CN＝，再证明△BFE∽△CEN，利用相似三角形性质即可求得答案．
【解答】解：∵四边形ABCD是正方形，AB＝6，
∴BC＝CD＝AB＝6，∠B＝∠C＝90°，
∵E是BC中点，
∴BE＝CE＝BC＝3，
设CN＝x，则DN＝6﹣x，
∵MN是线段DE的垂直平分线，
∴EN＝DN＝6﹣x，
在Rt△CEN中，CE2+CN2＝EN2，
∴32+x2＝（6﹣x）2，
解得：x＝，
∴CN＝，
∵EF⊥EN，
∴∠FEN＝90°，
∴∠BEF+∠CEN＝90°，
∵∠B＝∠C＝90°，
∴∠BEF+∠BFE＝90°，
∴∠BFE＝∠CEN，
∴△BFE∽△CEN，
∴＝，
∴BF＝＝＝4，
∴AF＝AB﹣BF＝6﹣4＝2．
故答案为：2．
【点评】本题考查了正方形的性质，线段垂直平分线的性质，勾股定理的应用，相似三角形的判定和性质等，熟练掌握相关性质定理是解题的关键．
6．（2022秋•大名县校级期末）如图，在等边三角形ABC中，点D、点E分别在BC、AC上，且∠ADE＝60°．
（1）写出和∠CDE相等的角： ∠BAD ；
（2）若AB＝3，BD＝1，则CE长为 ．
【分析】（1）利用等边三角形的性质可得∠B＝∠C＝60°，AB＝BC＝3，从而利用三角形的内角和定理可得∠BAD+∠ADB＝120°，再根据平角定义可得∠CDE+∠ADB＝120°，从而可得∠CDE＝∠BAD，即可解答；
（2）根据等边三角形的性质可得求出CD的长，再利用（1）的结论证明△ABD∽△DCE，然后利用相似三角形的性质进行计算即可解答．
【解答】解：（1）∵△ABC是等边三角形，
∴∠B＝∠C＝60°，AB＝BC＝3，
∴∠BAD+∠ADB＝180°﹣∠B＝120°，
∵∠ADE＝60°，
∴∠CDE+∠ADB＝180°﹣∠ADE＝120°，
∴∠CDE＝∠BAD，
∴和∠CDE相等的角：∠BAD，
故答案为：∠BAD；
（2）∵BC＝3，BD＝1，
∴CD＝BC﹣BD＝3﹣1＝2，
由（1）得：∠B＝∠C＝60°，∠CDE＝∠BAD，
∴△ABD∽△DCE，
∴＝，
∴＝，
∴CE＝，
故答案为：．
【点评】本题考查了等边三角形的性质，相似三角形的判定与性质，熟练掌握一线三等角模型相似是解题的关键．
7．（2022秋•盐湖区期末）如图，在△ABC中，AC＝3，BC＝4，∠C＝90°，过CB的中点D作DE⊥AD，交AB于点E，则EB的长为 ．
【分析】过点E作EM⊥BC，垂足为M，先证明一线三等角模型相似三角形△ACD∽△DME，从而利用相似三角形的性质可设EM＝2x，则DM＝3x，然后再证明A字模型相似三角形△BME∽△BCA，从而可得BM＝x，进而根据BD＝2列出关于x的方程，进行计算可求出EM，BM的长，最后在Rt△BME中，利用勾股定理进行计算即可解答．
【解答】解：过点E作EM⊥BC，垂足为M，
∴∠DME＝∠BME＝90°，
∴∠EDM+∠DEM＝90°，
∵DE⊥AD，
∴∠ADE＝90°，
∴∠CDA+∠EDM＝90°，
∴∠CDA＝∠DEM，
∵点D是BC的中点，
∴CD＝BD＝BC＝2，
∵∠C＝∠DME＝90°，
∴△ACD∽△DME，
∴＝＝，
∴设EM＝2x，则DM＝3x，
∵∠BME＝∠C＝90°，∠B＝∠B，
∴△BME∽△BCA，
∴＝，
∴＝，
∴BM＝x，
∵BD＝2，
∴DM+BM＝2，
∴3x+x＝2，
∴x＝，
∴EM＝，BM＝，
∴BE＝＝＝，
故答案为：．
【点评】本题考查了勾股定理，相似三角形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
8．（2022秋•武侯区校级期末）如图，E、F、G、H分别是矩形的边AB、BC、CD、AD上的点，AH＝CF，AE＝CG，∠EHF＝60°，∠GHF＝45°，∠EFB＝15°，若AH＝2，AD＝5+，则四边形EFGH的周长为 4（2+） ．
【分析】先构造15° 的直角三角形，求得15° 的余弦和正切值；作EK⊥FH，可求得EH：EF＝2：；作∠ARH＝∠BFT＝15°，分别交直线AB于R和T，构造“一线三等角”，先求得FT的长，进而根据相似三角形求得ER，进而求得AE，于是得出∠AEH＝30°，进一步求得结果．
【解答】解：如图1，
Rt△PMN中，∠P＝15°，NQ＝PQ，∠MQN＝30°，
设MN＝1，则PQ＝NQ＝2，MQ＝，PN＝+，
∴cs15°＝，tan15°＝2﹣，
如图2，
作EK⊥FH于K，作∠AHR＝∠BFT＝15°，分别交直线AB于R和T，
∵四边形ABCD是矩形，
∴∠BAD＝∠C，
在△AEH与△CGF中，
，
∴△AEH≌△CGF（SAS），
∴EH＝GF，
同理证得△EBF≌△GDH，则EF＝GH，
∴四边形EFGH是平行四边形，
设HK＝a，则EH＝2a，EK＝a，
∴EF＝EK＝a，
∵∠EAH＝∠EBF＝90°，
∴∠R＝∠T＝75°，
∵∠EHF＝60°，∠GHF＝45°，
∴∠EHG＝105°，
∵GH∥EF，
∴∠HEF＝75°，
∴∠R＝∠T＝∠HEF＝75°，
∵∠EFB＝15°，
∴∠EFT＝30°＝∠HER，
∴△FTE∽△ERH，
∵FT＝＝＝2，AR＝AH•tan15°＝4﹣2，
∴＝，
∴＝，
∴ER＝4，
∴AE＝ER﹣AR＝2，
∴tan∠AEH＝＝，
∴∠AEH＝30°，
∴HG＝2AH＝4，
∵∠BEF＝180°﹣∠AEH﹣∠HEF＝75°，
∴∠BEF＝∠T，
∴EF＝FT＝2，
∴EH+EF＝4+2＝2（2+），
∴2（EH+EF）＝4（2+），
∴四边形EFGH的周长为：4（2+），
故答案为：4（2+）．
【点评】本题属于四边形综合题，考查了矩形性质，全等三角形判定和性质，解直角三角形，构造15°特殊角的图形及其求15°的函数值，相似三角形的判定和性质等知识，解决问题的关键是作辅助线，构造“一线三等角”及构造15°直角三角形求其三角函数值．
三．解答题（共8小题）
9．（2023春•牟平区期末）如图，在△ABC中，D为BC上一点，BC＝AB＝3BD，求AD：AC的值．
【分析】由BC＝AB＝3BD，得，，易证△ABC∽△DBA，根据相似三角形的性质可得，即可求解．
【解答】解：∵BC＝AB＝3BD，
∴，，
∴，
又∵∠B＝∠B，
∴△ABC∽△DBA，
∴，
∴AD：AC＝1：．
【点评】本题考查了相似三角形的判定和性质，根据已知条件找到相似三角形是解题的关键．
10．（2022秋•德惠市期末）如图，在等边三角形ABC中，点D，E分别在BC，AB上，且∠ADE＝60°．
求证：△ADC∽△DEB．
【分析】依据△ABC是等边三角形，即可得到∠B＝∠C＝60°，再根据∠CAD＝∠BDE，即可判定△ADC∽△DEB．
【解答】证明：∵△ABC是等边三角形，
∴∠B＝∠C＝60°，
∴∠ADB＝∠CAD+∠C＝∠CAD+60°，
∵∠ADE＝60°，
∴∠ADB＝∠BDE+60°，
∴∠CAD＝∠BDE，
∴△ADC∽△DEB．
【点评】此题考查了相似三角形的判定与性质、等边三角形的性质等知识．解题时注意：有两组角对应相等的两个三角形相似．
11．（2022秋•武侯区期末）为了测量成都熊猫基地观光瞭望塔“竹笋”建筑物AB的高度，小军同学采取了如下方法：在地面上点C处平放一面镜子，并在镜子上做一个标记，然后人向后退，直至站在点D处恰好看到建筑物AB的顶端A在镜子中的像与镜子上的标记重合（如图所示）．其中B，C，D三点在同一条直线上．已知小军的眼睛距离地面的高度ED的长约为1.75m，BC和CD的长分别为40m和1m，求建筑物AB的高度．（说明：由物理知识，可知∠ECF＝∠ACF）
【分析】直接利用相似三角形的判定与性质得出＝，进而得出AB的长．
【解答】解：由题意可得：∠ABC＝∠EDC，∠ACB＝∠ECD，
故△ABC∽△EDC，
则＝，
∵小军的眼睛距离地面的高度ED的长约为1.75m，BC和CD的长分别为40m和1m，
∴＝，
解得：AB＝70，
答：这座建筑物的高度为70m．
【点评】本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
12．（2022秋•魏都区校级期末）如图，AB＝9，AC＝8，P为AB上一点，∠A＝∠CPD＝∠B，连接CD．
（1）若AP＝3，求BD的长；
（2）若CP平分∠ACD，求证：PD2＝CD•BD．
【分析】（1）利用一线三等角模型证明△ACP∽△BPD，即可解答；
（2）利用角平分线的性质可得∠PCD＝∠ACP，从而可得∠PCD＝∠DPB，然后证明△CPD∽△PBD，即可解答．
【解答】（1）解：∵AB＝9，AC＝3，
∴BP＝AB﹣AP＝9﹣3＝6，
∵∠A＝∠CPD，∠ACP+∠APC＝180°﹣∠A，∠APC+∠BPD＝180°﹣∠CPD，
∴∠ACP＝∠BPD，
∵∠A＝∠B，
∴△ACP∽△BPD，
∴＝，
∴＝，
∴BD＝，
∴BD的长为；
（2）证明：∵CP平分∠ACD，
∴∠PCD＝∠ACP，
∵∠ACP＝∠DPB，
∴∠PCD＝∠DPB，
∵∠CPD＝∠B，
∴△CPD∽△PBD，
∴＝，
∴PD2＝CD•BD．
【点评】本题考查了相似三角形的判定与性质，熟练掌握一线三等角模型是解题的关键．
13．（2023春•黄冈期末）同学们还记得吗？图①，图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形．受这两个图形的启发，数学兴趣小组提出了以下三个问题，请你回答：
【问题一】如图①，正方形ABCD的对角线相交于点O，点O又是正方形A1B1C1O的一个顶点，OA1交AB于点E，OC1交BC于点F，则AE与BF的数量关系为 AE＝BF ；
【问题二】受图①启发，兴趣小组画出了图③：直线m、n经过正方形ABCD的对称中心O，直线m分别与AD、BC交于点E、F，直线n分别与AB、CD交于点G、H，且m⊥n，若正方形ABCD边长为8，求四边形OEAG的面积；
【问题三】受图②启发，兴趣小组画出了图④：正方形CEFG的顶点G在正方形ABCD的边CD上，顶点E在BC的延长线上，且BC＝6，CE＝2．在直线BE上是否存在点P，使△APF为直角三角形？若存在，求出BP的长度；若不存在，说明理由．
【分析】【问题一】利用ASA判断出△AOE≌△BOF，即可得出答案；
（2）先求出S△AOB＝16，再利用ASA判断出△AOE≌△BOG，即可求出答案；
【问题三】分三种情况：利用三垂线构造出相似三角形，得出比例式求解，即可求出答案．
【解答】解：【问题一】∵正方形ABCD的对角线相交于点O，
∴OA＝OB，∠OAB＝∠OBA＝45°，∠AOB＝90°，
∵四边形A1B1C1O是正方形，
∴∠EOF＝90°，
∴∠AOE＝∠BOF，
∴△AOE≌△BOF（ASA），
∴AE＝BF，
故答案为：AE＝BF；
【问题二】如图③，
连接OA，OB，
∵点O是正方形ABCD的中心，
∴S△AOB＝S正方形ABCD＝×82＝16，
∵点O是正方形ABCD的中心，
∴∠OAE＝∠OBG＝45°，OA＝OB，∠AOB＝90°，
∵m⊥n，
∴∠EOG＝90°，
∴∠AOE＝∠BOG，
∴△AOE≌△BOG（ASA），
∴S△AOE＝S△BOG，
∴S四边形OEAG＝S△AOE+S△AOG＝S△BOG+S△AOG＝S△AOB＝16；
【问题三】在直线BE上存在点P，使△APF为直角三角形，
①当∠AFP＝90°时，如图④，延长EF，AD相交于点Q，
∵四边形ABCD和四边形CEFG是正方形，
∴EQ＝AB＝6，∠BAD＝∠B＝∠E＝90°，
∴四边形ABEQ是矩形，
∴AQ＝BE＝BC+CE＝8，EQ＝AB＝6，∠Q＝90°＝∠E，
∴∠EFP+∠EPF＝90，
∵∠AFP＝90°，
∴∠EFP+∠AFQ＝90°，
∴△EFP∽△QAF，
∴，
∵QF＝EQ﹣EF＝4，
∴，
∴EP＝1，
∴BP＝BE﹣EP＝7；
②当∠APF＝90°时，如图⑤，
同①的方法得，△ABP∽△PEF，
∴，
∵PE＝BE﹣BP＝8﹣BP，
∴，
∴BP＝2或BP＝6；
③当∠PAF＝90°时，如图⑥，
过点P作AB的平行线交DA的延长线于M，延长EF，AD相交于N，
同①的方法得，四边形ABPM是矩形，
∴PM＝AB＝6，AM＝BP，∠M＝90°，
同①的方法得，四边形ABEN是矩形，
∴AN＝BE＝8，EN＝AB＝6，
∴FN＝EN﹣EF＝4，
同①的方法得，△AMP∽△FNA，
∴，
∴，
∴AM＝3，
∴BP＝3，
即BP的长度为2或3或6或7．
【点评】此题是几何变换综合题，主要考查了正方形的性质，矩形的判定和性质，全等三角形的判定和性质，相似三角形的判定和性质，作出辅助线构造出相似三角形和全等三角形是解本题的关键．
14．（2022秋•郸城县期末）【感知】如图①，在正方形ABCD中，E为AB边上一点，连结DE，过点E作EF⊥DE交BC于点F．易证：△AED∽△BFE．（不需要证明）
【探究】如图②，在矩形ABCD中，E为AB边上一点，连结DE，过点E作EF⊥DE交BC于点F．
（1）求证：△AED∽△BFE．
（2）若AB＝10，AD＝6，E为AB的中点，求BF的长．
【应用】如图③，在△ABC中，∠ACB＝90°，AC＝BC，AB＝4．E为AB边上一点（点E不与点A、B重合），连结CE，过点E作∠CEF＝45°交BC于点F．当△CEF为等腰三角形时，BE的长为 2或2 ．
【分析】【探究】（1）利用同角的余角相等得∠ADE＝∠BEF，从而证明结论；
（2）由（1）知△AED∽△BFE，得，代入计算即可；
【应用】如果CE＝CF，则∠CEF＝∠CFE＝45°，∠ECF＝90°，则点E与点A重合，点F与点B重合，不符合题意；如果CE＝EF，利用AAS证明△AEC≌△BFE，得BE＝AC，可得答案；如果CF＝EF，则∠CEF＝∠ECF＝45°，则∠CFE＝90°，则CE⊥AB，从而解决问题．
【解答】【探究】（1）证明：∵四边形ABCD是矩形，
∴∠A＝∠B＝90°，
∴∠ADE+∠AED＝90°，
∵DE⊥EF，
∴∠DEF＝90°，
∴∠BEF+∠AED＝90°，
∴∠ADE＝∠BEF，
又∵∠A＝∠B，
∴△AED∽△BFE；
（2）解：∵E为AB的中点，
∴AE＝BE＝5，
由（1）知△AED∽△BFE，
∴，
即，
∴BF＝；
【应用】解：如果CE＝CF，则∠CEF＝∠CFE＝45°，∠ECF＝90°，则点E与点A重合，点F与点B重合，不符合题意，
②如果CE＝EF，则∠ECF＝∠EFC＝，
∵∠EFC为△BEF的外角，
∴∠EFC＝∠B+∠BEF，
∵∠ACB＝90°，AC＝BC，
∴∠A＝∠B＝45°，
∴∠BEF＝∠EFC﹣∠B＝67.5°﹣45°＝22.5°，
∠ACE＝90°﹣∠ECF＝90°﹣67.5°＝22.5°，
∴∠ACF＝∠BEF，
又∵∠A＝∠B，CE＝EF，
∴△AEC≌△BFE（AAS），
∴BE＝AC，
∵∠ACB＝90°，AC＝BC，AB＝4，
∴AC＝，
∴BE＝2；
如果CF＝EF，则∠CEF＝∠ECF＝45°，
∴∠CFE＝90°，
在△BEC中，∠B＝∠BCE＝45°，
∴∠BEC＝90°，
∴CE⊥AB，
又∵AC＝BC，
∴点E为AB的中点，
∴BE＝，
综上，BE的长为2或2，
故答案为：2或2．
【点评】本题是相似形综合题，主要考查了矩形的性质，全等三角形的判定与性质，相似三角形的判定与性质，等腰直角三角形的判定与性质，运用分类思想是解决【应用】的关键．
15．（2022秋•岚山区校级期末）【基础巩固】
（1）如图1，在△ABC中，∠ACB＝90°，直线l过点C，分别过A、B两点作AE⊥l，BD⊥l，垂足分别为E、D．求证：△BDC∽△CEA．
【尝试应用】
（2）如图2，在△ABC中，∠ACB＝90°，D是BC上一点，过D作AD的垂线交AB于点E．若BE＝DE，，AC＝20，求BD的长．
【拓展提高】
（3）如图3，在平行四边形ABCD中，在BC上取点E，使得∠AED＝90°，若AE＝AB，，CD＝，求平行四边形ABCD的面积．
【分析】（1）利用同角的余角相等可得∠BCD＝∠CAE．从而证明结论；
（2）过点E作EF⊥BC于点F．由（1）得△EDF∽△DAC．得．代入计算得DF＝16．从而得出BD的长；
（3）过点A作AM⊥BC于点M，过点D作DN⊥BC的延长线于点N．首先利用AAS证明△ABM≌△DCN，得BM＝CN，AM＝DN．设AM＝b，BE＝4a，EC＝3a．得BM＝ME＝CN＝2a，EN＝5a．再利用△AEM∽△EDN．得，从而解决问题．
【解答】（1）证明：∵∠ACB＝90°，
∴∠BCD+∠ACE＝90°，
∵AE⊥CE，
∴∠AEC＝90°，
∴ACE+∠CAE＝90°．
∴∠BCD＝∠CAE．
∵BD⊥DE，
∴∠BDC＝90°，
∴∠BDC＝∠AEC．
∴△BDC∽△CEA．
（2）解：过点E作EF⊥BC于点F．
由（1）得△EDF∽△DAC．
∴．
∵AD⊥DE，，AC＝20，
∴，
∴DF＝16．
∵BE＝DE，
∴BF＝DF．
∴BD＝2DF＝32．
（3）解：过点A作AM⊥BC于点M，过点D作DN⊥BC的延长线于点N．
∴∠AMB＝∠DNC＝90°．
∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝CD．
∴∠B＝∠DCN．
∴△ABM≌△DCN（AAS）．
∴BM＝CN，AM＝DN．
∵AB＝AE，AM⊥BC，
∴BM＝ME，
∵，
设AM＝b，BE＝4a，EC＝3a．
∴BM＝ME＝CN＝2a，EN＝5a．
∵∠AED＝90°，
由（1）得△AEM∽△EDN．
∴，
∴，
∴，
∵，
∴（2a）2+b2＝14，
∴a＝1，．
∴平行四边形ABCD的面积＝．
【点评】本题是相似形综合题，主要考查了平行四边形的性质，等腰三角形的性质，相似三角形的判定与性质，构造一线三等角相似是解题的关键．
16．（2022秋•黄浦区期末）已知，如图1，在四边形ABCD中，∠BAC＝∠ADC＝90°，CD＝4，cs∠ACD＝．
（1）当BC∥AD时（如图2），求AB的长；
（2）联结BD，交边AC于点E，
①设CE＝x，AB＝y，求y关于x的函数解析式并写出定义域；
②当△BDC是等腰三角形时，求AB的长．
【分析】（1）由锐角三角函数定义得AC＝5，再由勾股定理得AD＝3，然后证△ABC∽△DCA，即可解决问题；
（2）①过D作DN⊥AC于点N，由三角形面积得DN＝，再由勾股定理得CN＝，然后证△BAE∽△DNE，即可解决问题；
②分两种情况，a、当BC＝BD时，过B作BQ⊥CD于点Q，过A作AP⊥BQ于点P，则CQ＝DQ＝CD＝2，四边形APQD是矩形，再证△APB∽△ADC，即可求解；
b、当BD＝CD＝4时，过B作BM⊥直线AD于点M，证△BMA∽△ADC，得＝，设BM＝3k，则AM＝4k，然后由勾股定理得出方程，解方程，即可得出结论．
【解答】解：（1）∵∠ADC＝90°，
∴cs∠ACD＝＝，
∴AC＝CD＝×4＝5，
∴AD＝＝＝3，
∵BC∥AD，
∴∠ACB＝∠DAC，
∵∠BAC＝∠ADC＝90°，
∴△ABC∽△DCA，
∴＝，
即＝，
∴AB＝，
即AB的长为；
（2）①如图1，过D作DN⊥AC于点N，则∠DNE＝∠DNC＝90°，
∵∠ADC＝90°，
∴S△ACD＝AC•DN＝AD•CD，
∴DN＝＝＝，
∴CN＝＝＝，
∴AN＝AC﹣CN＝5﹣＝，
∵CE＝x，
∴AE＝AC﹣CE＝5﹣x，EN＝CE﹣CN＝x﹣，
∵AE＞0，EN＞0，
∴＜x＜5，
∵∠BAE＝∠DNE＝90°，∠AEB＝∠NED，
∴△BAE∽△DNE，
∴＝，
即＝，
∴y＝＝，
即y关于x的函数解析式为y＝（＜x＜5）；
②∵∠BAC＝90°，
∴BC＞AC，
∵AC＝5，CD＝4，
∴BC＞CD，
分两种情况：
a、当BC＝BD时，如图3，
过B作BQ⊥CD于点Q，过A作AP⊥BQ于点P，
则CQ＝DQ＝CD＝2，四边形APQD是矩形，
∴AP＝DQ＝2，∠PAD＝90°，
∵∠BAC＝90°，
∴∠PAD＝∠BAC，
∴∠BAP＝∠CAD，
∵∠APB＝∠ADC＝90°，
∴△APB∽△ADC，
∴＝，
即＝，
解得：AB＝；
b、当BD＝CD＝4时，如图4，
过B作BM⊥直线AD于点M，
则∠BMA＝∠BAC＝∠ADC＝90°，
∴∠ABM+∠BAM＝∠CAD+∠BAM＝90°，
∴∠ABM＝∠CAD，
∴△BMA∽△ADC，
∴＝＝，
设BM＝3k，则AM＝4k，
∴DM＝AD+AM＝3+4k，
在Rt△BDM中，由勾股定理得：BD2＝BM2+DM2，
即42＝（3k）2+（3+4k）2，
整理得：25k2+24k﹣7＝0，
解得：k1＝，k2＝（不符合题意舍去），
∴AB＝＝＝5k＝；
综上所述，当△BDC是等腰三角形时，AB的长为或．
【点评】本题是四边形综合题目，考查了矩形的判定与性质、梯形的性质、相似三角形的判定与性质、勾股定理、等腰三角形的性质、锐角三角函数定义以及分类讨论等知识，本题综合性强，熟练掌握矩形的判定与性质，证明三角形相似是解题的关键，属于中考常考题型．
题型四：手拉手模型-旋转型相似
一．填空题（共4小题）
1．（2022秋•鼓楼区校级期末）如图，在△ABC中，AB＝AC＝3，BC＝6，点P在边AC上运动（可与点A，C重合），将线段BP绕点P逆时针旋转120°，得到线段DP，连接BD，CD，则CD长的最小值为 ．
【分析】以BC为边构建出和△BPD相似的三角形，通过将CD边转化为其他边来求值．
【解答】解：如图所示，以BC为底边向上作等腰△BQC，使∠BQC＝120°，连接PQ．
由题意可得△BQC和△BPD均为顶角为120° 的等腰三角形，
可得，∠QBC＝∠PBD＝30°，
∴∠QBC﹣∠QBD＝∠PBD﹣∠QBD，
∴∠PBQ＝∠DBC，
∴△PBQ∽△DBC，
∴，
∴当PQ⊥AC时，有PQ最小，即此时CD最小，
如图所示，设OP′⊥AC，延长AQ与BC交K，此时QP'为QP的最小值，
可得AK⊥BC，
∵△BQC中，∠BQC＝120°，BC＝6，
∴BK＝3，∠QBK＝30°，
∴QK＝，
∵AB＝AC＝3，KC＝3，
∴AK＝＝6，
∴AQ＝AK﹣QK＝5，
∵∠AP'Q＝∠AKC＝90°，∠QAP'＝∠CAK，
∴△AQP'∽△ACK，
∴，
∴，
∴QP'＝，
∴CD＝P′＝．
【点评】本题考查的是瓜豆原理的知识点，重难点在于构造相似三角形的手拉手模型，属于难题．
2．（2022秋•建邺区期末）如图，在△ABC中，∠ACB＝90°，∠A＝32°，点D是线段AB上一动点，作△CDE∽△CAB，连接BE．若△BCE是等腰三角形，则∠CDB＝ 64°或106° ．
【分析】分三种情况讨论，由相似三角形的性质，等腰三角形的性质即可解决问题．
【解答】解：∵△CDE∽△CAB，
∴AC：CD＝BC：CE，∠ACB＝∠DCE，∠CED＝∠CBA，
∴∠ACD＝∠BCE，
∴△ACD∽△BCE，
∴∠ADC＝∠CEB，∠CBE＝∠A＝32°，
∵∠ACB＝90°，
∴∠CBA＝90°﹣32°＝58°，
∴∠CED＝58°，
当CE＝BE时，
∠ECB＝∠CBE＝32°，
∴∠BEC＝180°﹣∠ECB﹣∠CBE＝116°，
∴∠ADC＝∠BEC＝116°，
∴∠CDB＝180°﹣116°＝64°；
当BC＝CE时，
∠BCE＝∠BEC＝×（180°﹣32°）＝74°，
∴∠ADC＝∠BEC＝74°，
∴∠CDB＝180°﹣74°＝106°，
当BC＝CE时，
∵∠CEB＞∠CED＝CBA＝58°，∠CBE＝∠A＝32°，
∴∠CEB＞∠CBE，
∴BC≠CE，
∴∠CDB＝64°或106°．
故答案为：64°或106°．
【点评】本题考查相似三角形的判定和性质，等腰三角形的性质，关键是要分三种情况讨论．
3．（2022秋•黄浦区期末）如图，在矩形ABCD中，过点D作对角线AC的垂线，垂足为E，过点E作BE的垂线，交边AD于点F，如果AB＝3，BC＝5，那么DF的长是 ．
【分析】利用矩形的性质求出AC，利用三角形的面积、勾股定理求出DE、CE的长，再利用等角的余角相等说明∠BAE＝∠ADE、∠AEB＝∠DEF，得△DEF∽△BEA，最后利用相似三角形的性质得结论．
【解答】解：∵四边形ABCD是矩形，
∴∠ABC＝∠ADC＝90°，AB＝CD＝3，BC＝AD＝5，AB∥CD，
∴AC＝＝＝．
∵S△ADC＝AD•CD＝AC•DE，
∴DE＝．
∵DE⊥AC，
∴CE＝＝＝．
∴AE＝AC﹣CE＝．
∵AB∥CD，
∴∠BAE＝∠DCA．
∵∠DCA+∠CDE＝∠CDE+∠ADE＝90°，
∴∠BAE＝∠ADE．
∵BE⊥FE，DE⊥AC，
∴∠FEA+∠AEB＝∠DEF+∠FEA＝90°．
∴∠AEB＝∠DEF．
∴△DEF∽△BEA．
∴＝＝．
∴DF＝×3＝．
故答案为：．
【点评】本题主要考查了相似三角形，掌握相似三角形的性质与判定、三角形的内角和定理及勾股定理是解决本题的关键．
4．（2022秋•黔江区期末）如图，点A在线段BD上，在BD的同侧作等腰直角△ABC和等腰直角△ADE，CD与BE、AE分别交于点P，M．对于下列结论：①△BAE∽△CAD；②MP•MD＝MA•ME；③2CB2＝CP•CM；④sin∠CPB＝；其中正确的结论有 ①②③ ．（写出所有正确结论的序号）．
【分析】根据题意可得：CA＝AB，AD＝AE，利用两角成比例且夹角相等的两个三角形相似，证明①△BAE∽△CAD，从而得∠AEB＝∠ADC，然后利用两角相等的两个三角形相似证明△EMP∽△DMA，从而证明②MP•MD＝MA•ME，利用②的结论再证明△DEM∽△APM，从而得∠APM＝∠DEM＝90°，根据已知可知∠EAC＝90°，然后利用射影定理证明③2CB2＝CP•CM，求出∠CPB的度数即可判断．
【解答】解：∵△ABC和△ADE都是等腰直角三角形，
∴CA＝AB，AD＝AE，∠AED＝∠ABC＝90°，∠DAE＝∠CAB＝45°，
∴∠DAE+∠EAC＝∠CAB+∠EAC，
∴∠DAC＝∠EAB，
∵＝＝，
∴△BAE∽△CAD，
故①正确；
∵△BAE∽△CAD，
∴∠AEB＝∠ADC，
∵∠PME＝∠AMD，
∴△EMP∽△DMA，
∴＝，
∴MP•MD＝MA•ME，
故②正确；
∵MP•MD＝MA•ME，
∴＝，
∵∠AMP＝∠DME，
∴△DEM∽△APM，
∴∠APM＝∠DEM＝90°，
∵∠DAE＝∠CAB＝45°，
∴∠EAC＝180°﹣（∠DAE+∠CAB）＝90°，
∴∠EAC＝∠APC，
∵∠ACP＝∠ACM，
∴△CPA∽△CAM，
∴＝，
∴CA2＝CP•CM，
∴2CB2＝CP•CM，
故③正确；
设BE与AC相交于点F，
∵△BAE∽△CAD，
∴∠ACD＝∠ABE，
∵∠AFB＝∠PFC，
∴∠CPB＝∠CAB＝45°，
∴sin∠CPB＝，
故④错误，
所以，正确的结论有：①②③，
故答案为：①②③．
【点评】本题考查了解直角三角形，相似三角形的判定与性质，等腰直角三角形，熟练掌握手拉手模型的相似三角形是解题的关键．
二．解答题（共11小题）
5．（2023春•钢城区期末）如图，已知△ABC和△ADE，AB＝AC，AD＝AE，点D在BC边上，∠BAD＝∠CAE，边DE与AC相交于点F．
（1）求证：△ABC∽△ADE；
（2）如果AE∥BC，DA＝DC，连结CE．
求证：四边形ADCE是菱形．
【分析】（1）由等角加同角相等可得∠BAC＝∠DAE，由△ABC和△ADE的顶角相等，且都是等腰三角形，以此即可证明△ABC∽△ADE；
（2）根据平行线的性质得∠AEF＝∠CDF，∠EAF＝∠DCF，进而得到∠ADF＝∠CDF，由等腰三角形三线合一的性质可得AF＝CF，再通过AAS证明△AEF≌△CDF，得到AE＝CD，由对边平行且相等的四边形是平行四边形可证明四边形ADCE为平行四边形，最后根据一组邻边相等的平行四边形是菱形即可证明四边形ADCE是菱形．
【解答】（1）证明：∵∠BAD＝∠CAE，
∴∠BAD+∠CAD＝∠CAE+CAD，即∠BAC＝∠DAE，
∵AB＝AC，AD＝AE，
∴∠B＝∠ACB＝，∠ADE＝∠E＝，
∵∠BAC＝∠DAE，
∴∠B＝∠ACB＝∠ADE＝∠E，
∴△ABC∽△ADE；
（2）证明：如图，
∵AE∥BC，
∴∠AEF＝∠CDF，∠EAF＝∠DCF，
由（1）可知，∠DCF＝∠ADF＝∠AEF，
∴∠ADF＝∠CDF，
∵DA＝DC，
∴AF＝CF，
在△AEF和△CDF中，
，
∴△AEF≌△CDF（AAS），
∴AE＝CD，
∵AE∥CD，AE＝CD，
∴四边形ADCE为平行四边形，
∵DA＝DC，
∴平行四边形ADCE为菱形．
【点评】本题主要考查相似三角形的判定、等腰三角形的性质、平行线的性质、全等三角形的判定与性质，熟练菱形的判定方法是解题关键．菱形的判定：①菱形定义：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等＝菱形）．②四条边都相等的四边形是菱形．③对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．
6．（2023春•永城市期末）如图，点E在正方形ABCD的AD边上（不与点A，D重合），连接EC，将△DEC沿EC翻折，使点D落在点F处，作射线DF交CE于点M，交AB于点N，连接BF．
（1）求证：△ADN≌△DCE；
（2）过点A作AH∥BF交射线DN于点H．
①求∠AHF的度数；
②直接写出线段AH与FM之间的数量关系．
【分析】（1）在△ADN与△DCE中找对应的边和角相等；
（2）①猜想∠AHF＝45°，根据AH∥BF，只要说明∠BFN＝45°，再寻求角角关系；
②由∠BFN＝45°猜想△BHF是等腰直角三角形，正方形中也可构造等腰直角三角形，利用手拉手模型证明三角形相似．
【解答】（1）证明：∵△DEC沿EC翻折，点D落在点F处，
∴EF＝ED，CF＝CD，
∴CE垂直平分DF，
∴在Rt△EMD中，∠DEM+∠EDM＝90°，
∵四边形ABCD是正方形，
∴∠ADC＝∠DAB＝90°，AD＝DC，
∴在Rt△ECD中，∠DEC+∠ECD＝90°，
∴∠EDM＝∠ECD，
∴△ADN≌△DCE（ASA）．
（2）解：①由翻折知，CD＝CF．
∵四边形ABCD是正方形，
∴CD＝CB，∠DCB＝90°，
∴CD＝CF＝CB，
∴∠CDF＝∠CFD，∠CFB＝∠CBF，
∴∠DCF＝180°﹣（∠CDF+∠CFD）＝180°﹣2∠CFD，∠FCB＝180°﹣（∠CFB+∠CBF）＝180°﹣2∠CFB，
∵∠DCF+∠FCB＝∠DCB＝90°，
∴180°﹣2∠CFD+180°﹣2∠CFB＝90°，
∴∠CFD+∠CFB＝135°，
∴∠BFN＝180°﹣135°＝45°，
∵AH∥BF，
∴∠AHF＝∠BFN＝45°．
②连接HB，BD，
∵∠AHD＝∠ABD＝45°，
∴A、H、B、D四点共圆，
∴∠BHD＝∠BAD＝90°，
∴△BHF是等腰直角三角形，
∴∠HBF＝45°，
∵∠ABD＝45°，
∴∠HBF＝∠ABD，
∴∠HBA＝∠FBD，
∵＝＝，
∴△BHA∽△BFD，
∴＝，
∴＝，
∴．
【点评】本题考查了三角形全等的判断，平行线的性质，三角形相似等知识点，关键要善于联想，大胆猜测，向熟知的题型上靠．
7．（2022秋•东河区期末）如图，在△ABC和△ADE中，∠DAB＝∠EAC，∠C＝∠E．
（1）求证：AD•BC＝AB•DE；
（2）若S△ADE：S△ABC＝4：9，BC＝6，求DE的长．
【分析】（1）由∠DAB＝∠EAC，得到∠DAE＝∠CAB，又∠E＝∠C，推出△ADE∽△ABC，即可证明问题；
（2）由相似三角形面积的比等于相似比的平方即可求出DE的长．
【解答】（1）证明：∵∠DAB＝∠EAC，
∴∠DAB+BAE＝∠EAC+∠BAE，
∴∠DAE＝∠CAB，
∵∠E＝∠C，
∴△ADE∽△ABC，
∴AD：AB＝DE：BC，
∴AD•BC＝AB•DE；
（2）解；∵△ADE∽△ABC，
∴＝＝，
∴＝，
∴DE＝4．
∴DE的长是4．
【点评】本题考查相似三角形，关键是掌握相似三角形的性质．
8．（2022秋•建邺区期末）如图，点E在线段BC上，AB⊥BC，DC⊥BC，∠AED＝90°．求证AB•CD＝BE•EC．
【分析】先利用直角三角形的两个锐角互余和平角说明∠BAE＝∠DEC，再判断△ABE∽△ECD，最后利用相似三角形的性质得结论．
【解答】证明：∵AB⊥BC，DC⊥BC，
∴∠B＝90°，∠C＝90°．
∵∠AED＝90°，
∴∠AEB+∠DEC＝90°．
∵∠BAE+∠AEB＝90°，
∴∠BAE＝∠DEC．
又∵∠B＝∠C，
∴△ABE∽△ECD．
∴＝．
∴AB•CD＝BE•EC．
【点评】本题主要考查了相似三角形，掌握相似三角形的判定和性质是解决本题的关键．
9．（2022秋•大东区期末）如图，D为△ABC内的一点，E为△ABC外的一点，且∠ABC＝∠DBE，∠BAD＝∠BCE．
（1）求证：△ABD∽△CBE；
（2）若AB：DB＝5：2，AC＝6，直接写出线段DE的长度为 2.4 ．
【分析】（1）由∠ABC＝∠DBE得到∠ABD＝∠CBE，又∠BAD＝∠BCE，即可证明△ABD∽△CBE；
（2）由△ABD∽△CBE，得到AB：BD＝BC：BE，又∠ABC＝∠DBE，推出△ABC∽△DBE，得到AB：BD＝AC：DE，即可求出DE的长．
【解答】（1）证明：∵∠ABC＝∠DBE，
∴∠ABD+∠DBC＝∠CBE+∠DBC，
∴∠ABD＝∠CBE，
∵∠BAD＝∠BCE，
∴△ABD∽△CBE；
（2）解：∵△ABD∽△CBE，
∴AB：BD＝BC：BE，
∵∠ABC＝∠DBE，
∴△ABC∽△DBE，
∴AB：BD＝AC：DE，
∴6：DE＝5：2，
∴DE＝2.4，
∴DE的长是2.4．
故答案为：2.4．
【点评】本题考查相似三角形的判定和性质，关键是掌握相似三角形的判定方法．
10．（2022秋•松原期末）已知△ABC是等腰三角形，AB＝AC，将△ABC绕点B逆时针旋转得到△A'BC'，点A、点C的对应点分别是点A′、点C′．
感知：如图①，当BC'落在AB边上时，∠A'AB与∠C′CB之间的数量关系是 相等 （不需要证明）；
探究：如图②，当BC′不落在AB边上时，∠A′AB与∠C′CB是否相等？如果相等，请证明；如果不相等，请说明理由；
应用：如图③，若∠BAC＝90°，AA'、CC′交于点E，则∠A′EC＝ 135 度．
【分析】感知：由旋转知，△BCC'，BAA'是顶角相等的等腰三角形，从而得出答案；
探究：由旋转知，可证明△ABA'∽△CBC'，从而结论不变；
应用：设C'B与AE相交于点O，由C'B＝CB，得∠C'CB＝∠CC'B，则∠BA'A＝∠CC'B，再利用三角形内角和解决问题．
【解答】解：感知：∵将△ABC绕点B逆时针旋转得到△A'BC'，
∴∠A'BC'+∠C'BA＝∠ABC+∠C'BA，
即∠A'BA＝∠C'BC，
又∵A'B＝AB，C'B＝BC，
∴，
即∠A'AB＝∠C'CB，
故答案为：相等；
探究：∠A'AB＝∠C'CB，证明如下：
∵将△ABC绕点B逆时针旋转得到△A'BC'，
∴BC＝BC'，BA＝BA'，∠CBC'＝∠ABA'，
∴，
∴△ABA'∽△CBC'，
∴∠A'AB＝∠C'CB；
应用：∵C'B＝CB，
∴∠C'CB＝∠CC'B，
∴∠BA'A＝∠CC'B，
设C'B与AE相交于点O，
∵∠A'OB＝∠C'OE，
∴∠C'EO＝∠OBA'＝∠ACB，
∵AB＝AC，∠BAC＝90°，
∴∠ACB＝45°＝∠C'EO，
∴∠A'EC＝180°﹣∠C'EO＝135°．
【点评】本题是几何变换综合题，主要考查了等腰三角形的性质，旋转的性质，相似三角形的判定与性质等知识，证明△ABA'∽△CBC'是解题的关键．
11．（2022秋•靖江市期末）如图，已知△ABC中，∠ACB＝90°，AC＝BC，点D、E在边AB上，CE2＝BE•DE．
（1）求证：∠DCE＝45°；
（2）当AC＝3，AD＝2BD时，求DE的长．
【分析】（1）先利用等腰直角三角形的性质求出∠B，再利用“两边对应成比例，夹角相等”判断△CDE∽△BCE，最后利用相似三角形的性质得结论；
（2）先利用等腰直角三角形的性质及勾股定理求出AB、AD、BD的长，再判断△BEC∽△ACD，利用相似三角形的性质求出BE，最后利用线段的和差关系得结论．
【解答】（1）证明：∵∠ACB＝90°，AC＝BC，
∴∠B＝∠A＝45°．
∵CE2＝BE•DE，
∴＝．
又∵∠BEC＝∠BEC，
∴△CDE∽△BCE．
∴∠ECD＝∠B＝45°．
（2）解：∵∠ACB＝90°，AC＝BC＝3，
∴∠B＝∠A＝45°，AB＝＝3．
∵AD＝2BD，AD+BD＝AB，
∴3BD＝3．
∴BD＝，AD＝2．
∵∠BEC＝∠A+∠ACE，∠DCE+∠ACE＝∠ACD．
∠A＝∠DCE＝45°，
∴∠BEC＝∠ACD．
∵∠A＝∠B＝45°，
∴△BEC∽△ACD．
∴＝，即＝．
∴BE＝．
∵BD+DE＝BE，
∴DE＝BE﹣BD＝﹣＝．
【点评】本题主要考查了相似三角形，掌握等腰直角三角形的性质、勾股定理及相似三角形的性质和判定是解决本题的关键．
12．（2022秋•静安区期末）在等腰直角△ABC中，∠C＝90°，AC＝4，点D为射线CB上一动点（点D不与点B、C重合），以AD为腰且在AD的右侧作等腰直角△ADF，∠ADF＝90°，射线AB与射线FD交于点E，联结BF．
（1）如图所示，当点D在线段CB上时，
①求证：△ACD∽△ABF；
②设CD＝x，tan∠BFD＝y，求y关于x的函数解析式，并写出x的取值范围；
（2）当AB＝2BE时，求CD的长．
【分析】（1）①利用等腰直角三角形的性质和两边对应成比例且夹角相等的两个三角形相似解答即可；
②过点E作EH⊥BD于点H，设BH＝HE＝m，利用相似三角形的拍等于性质和直角三角形的边角关系定理解答即可；
（2）利用分类讨论的思想方法，画出图形，列出关于x的方程，解方程即可得出结论．
【解答】（1）①证明：∵△ABC和△ADF是等腰直角三角形，
∴AB＝AC，AF＝AD，∠CAB＝∠DAF＝45°．
∴，∠CAD＝∠BAF，
∴△ACD∽△ABF；
②解：过点E作EH⊥BD于点H，如图，
∵△ABC是等腰直角三角形，
∴∠ABC＝45°，
∵EH⊥BD，
∴BH＝HE．
设BH＝HE＝m，则BE＝m，
∴DH＝BC﹣CD﹣BH＝4﹣x﹣m．
∵∠ADF＝90°，
∴∠ADC+∠FDH＝90°，
∵∠CAD+∠ADC＝90°，
∴∠CAD＝∠FDH．
∵∠ACD＝∠DHE＝90°，
∴△ACD∽△DHE，
∴，
∴，
∴m＝，
∴BH＝HE＝．
由①知：△ACD∽△ABF，
∴∠ACD＝∠ABF＝90°．
∵∠ADF＝90°，
∴∠ADF＝∠ABF＝90°．
∵∠AED＝∠BEF，
∴∠BFD＝∠DAE．
∴tan∠BFD＝tan∠DAE＝．
∵△ACD∽△DHE，
∴，
∴y＝tan∠BFD＝＝，
∴y关于x的函数解析式y＝，x的取值范围：0＜x＜4；
（2）①解：当点D在线段CB上时，如图，
由（1）②知：BH＝HE＝．
∴BE＝BH＝•．
∵AB＝2BE，AB＝AC＝4，
∴4＝2ו，
∴8+2x＝4x﹣x2，
∴x2﹣2x+8＝0．
∵Δ＝（﹣2）2﹣4×1×8＝4﹣32＝﹣28＜0，
∴此方程没有实数根，
∴当点D在线段CB上时，不存在AB＝2BE；
②当点D在线段CB的延长线上时，如图，
过点E作EH⊥BD于点H，
∵△ABC和△ADF是等腰直角三角形，
∴AB＝AC，AF＝AD，∠CAB＝∠DAF＝45°．
∴，∠CAD＝∠BAF，
∴△ACD∽△ABF．
∴∠ACD＝∠ABF＝90°．
∵△ABC是等腰直角三角形，
∴∠ABC＝45°，
∴∠EBH＝∠ABC＝45°．
∵EH⊥BD，
∴BH＝HE．
设BH＝HE＝n，则BE＝n，
∴DH＝CD﹣BC﹣BH＝x﹣4﹣n．
∵∠ADF＝90°，
∴∠ADE＝90°，
∴∠ADC+∠EDH＝90°，
∵∠CAD+∠ADC＝90°，
∴∠CAD＝∠EDH．
∵∠ACD＝∠DHE＝90°，
∴△ACD∽△DHE，
∴，
∴，
∴n＝．
∴BH＝HE＝．
∴BE＝BH＝•．
∵AB＝2BE，AB＝4，
∴4＝2ו．
∴8+2x＝x2﹣4x，
∴x2﹣6x﹣8＝0，
解得：x＝＝3±，
∵x＞0，
∴x＝3+．
∴CD＝3+．
综上，当AB＝2BE时，CD的长为3+．
【点评】本题主要考查了等腰直角三角形的性质，直角三角形的性质，相似三角形的判定与性质，函数的解析式，一元二次方程的解法，本题是相似三角形的综合题，熟练掌握相似三角形的判定与性质是解题的关键．
13．（2022秋•驿城区期末）已知在Rt△ABC中，CD⊥AB于点D．
（1）在图1中，写出其中两对相似三角形．
（2）已知BD＝1，DC＝2，将△CBD绕着点D按顺时针方向进行旋转得到△C'BD，连接AC'，BC．
①如图2，判断AC'与BC之间的位置及数量关系，并证明；
②在旋转过程中，当点A，B，C'在同一直线时，求BC的长．
【分析】（1）利用两个角相等可得△ABC∽△ACD，△BCD∽△BAC；
（2）①利用两边成比例且夹角相等证明△DBC∽△DC'A，得，∠DC'A＝∠DBC，可得结论；
②分点C'在线段AB或AB的延长线两种情形，分别画出图形，利用勾股定理列方程可得答案．
【解答】解：（1）∵CD⊥AB，
∴∠ADC＝∠BDC＝∠ACB＝90°，
∴△ABC∽△ACD，△BCD∽△BAC；
（2）①，AC'⊥BC，理由如下：
由（1）知，在图1中，△ABC∽△CBD∽△ACD，
∴，
如图2，∵∠BDC'＝∠CDA＝90°，
∴∠BDC＝∠C'DA，
∴△DBC∽△DC'A，
∴，∠DC'A＝∠DBC，
∵∠DEB＝∠CEC'，
∴∠C'FE＝∠BDC'＝90°，
∴AC'⊥BC，
∴，AC'⊥BC；
②如图，当点A、B、C'在同一直线上时，
由①知，，AC'⊥BC，
设BC＝x，AC'＝2x，
在Rt△ACB中，由勾股定理得，x2+（2x﹣）2＝（2）2，
解得x＝（负值舍去），
如图，当A、C'、B在同一直线上时，
同理可得，x2+（2x+）2＝（2）2，
解得x＝（负值舍去），
综上：BC＝或．
【点评】本题是相似形综合题，主要考查了相似三角形的判定与性质，旋转的性质，勾股定理等知识，熟练掌握手拉手模型﹣旋转相似是解题的关键．
14．（2022秋•梅里斯区期末）在△ABC中，AB＝AC，点D为AB边上一动点，∠CDE＝∠BAC＝α，CD＝ED，连接BE，EC．
（1）问题发现：
如图①，若α＝60°，则∠EBA＝ 120° ，AD与EB的数量关系是 AD＝EB ；
（2）类比探究：
如图②，当α＝90°时，请写出∠EBA的度数及AD与EB的数量关系并说明理由；
（3）拓展应用：
如图③，点E为正方形ABCD的边AB上的三等分点，以DE为边在DE上方作正方形DEFG，点O为正方形DEFG的中心，若OA＝，请直接写出线段EF的长度．
【分析】（1）证明△ACD≌△BCE（SAS），得AD＝EB，∠CBE＝∠A＝60°，则∠EBA＝∠ABC+∠CBE＝120°；
（2）证△DEC∽△ABC，∠BCE＝∠ACD，得，再证△BCE∽△ACD，得∠EBC＝∠DAC＝90°，＝，则∠EBA＝∠EBC+∠ABC＝135°，进而得出结论；
（3）连接BD，①当AE＝AB时，证△AOD∽△BED，得，求出AB＝3＝AD，则AE＝1，在Rt△AED中，由勾股定理求出ED＝即可；
②当BE＝AB时，同①得：，求出AB＝6＝AD，则AE＝4，在Rt△AED中，由勾股定理得ED＝2即可．
【解答】解：（1）∵α＝60°，
∴∠ABC＝α＝60°，∠CDE＝α＝60°，
∵AB＝AC，CD＝ED，
∴△ABC和△CDE是等边三角形，
∴AC＝BC，CD＝CE，∠ABC＝∠ACB＝∠A＝∠DCE＝60°，
∴∠ACD＝∠BCE，
∴△ACD≌△BCE（SAS），
∴AD＝EB，∠CBE＝∠A＝60°，
∴∠EBA＝∠ABC+∠CBE＝120°，
故答案为：120°，AD＝EB；
（2）∠EBA＝135°，EB＝AD，
理由如下：
∵α＝90°，
∴∠CDE＝∠BAC＝90°，
∵CD＝ED，AB＝AC，
∴∠DEC＝∠DCE＝∠ABC＝∠ACB＝45°，
∴△DEC∽△ABC，∠BCE＝∠ACD，
∴，
∴，
∴△BCE∽△ACD，
∴∠EBC＝∠DAC＝90°，，
∴∠EBA＝∠EBC+∠ABC＝90°+45°＝135°，
∵，
∴，
∴EB＝AD；
（3）连接BD，分两种情况：
①当AE＝AB时，如图③所示：
∵四边形DEFG是正方形，
∴EF＝ED，对角线FD与EG互相垂直平分，
∴△DEO是等腰直角三角形，
∴＝sin45°＝，
在Rt△ABD中，＝sin45°＝，
∴，
∵∠ODA+∠ADE＝45°＝∠BDE+∠ADE，
∴∠ODA＝∠BDE，
∴△AOD∽△BED，
∴，
∴，
∵OA＝，
∴AB＝3＝AD，
∴AE＝AB＝1，
在Rt△AED中，由勾股定理得：ED＝＝＝，
∴EF＝ED＝；
②当BE＝AB时，如图④所示：
同①得：，
∴，
∵OA＝，
∴AB＝6＝AD，
∴AE＝AB＝4，
在Rt△AED中，由勾股定理得：ED＝＝＝2，
∴EF＝ED＝2；
综上所述，线段EF的长度为或2．
【点评】本题是四边形综合题目，考查了正方形的性质、等边三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理、锐角三角函数定义等知识；本题综合性强，熟练掌握正方形的性质、等边三角形的判定与性质，证明三角形全等和三角形相似是解题的关键．
15．（2023春•广饶县期末）某校数学活动小组在一次活动中，对一个数学问题作如下探究：
（1）问题发现：如图1，在等边△ABC中，点P是边BC上任意一点，连接AP，以AP为边作等边△APQ，连接CQ，∠ABC与∠ACQ的数量关系是 ∠ABC＝∠ACQ ；
（2）变式探究：如图2，在等腰△ABC中，AB＝BC，点P是边BC上任意一点，以AP为腰作等腰△APQ，使AP＝PQ，∠APQ＝∠ABC，连接CQ，判断∠ABC和∠ACQ的数量关系，并说明理由；
（3）解决问题：如图3，在正方形ADBC中，点P是边BC上一点，以AP为边作正方形APEF，Q是正方形APEF对角线的交点，连接CQ．若正方形APEF的边长为10，，求正方形ADBC的边长．
【分析】（1）利用SAS定理证明△BAP≌△CAQ，根据全等三角形的性质解答；
（2）先证明△BAC∽△PAQ，得到，再证明△BAP∽△CAQ，根据相似三角形的性质解答即可；
（3）根据相似三角形的性质求出BP，根据勾股定理列出方程，解方程得到答案．
【解答】解：（1）∵△ABC和△APQ都是等边三角形，
∴AB＝AC，AP＝AQ，∠BAC＝∠PAQ＝60°，
∴∠BAP＝∠CAQ，
在△BAP和△CAQ中，
，
∴△BAP≌△CAQ（SAS），
∴∠ABC＝∠ACQ，
故答案为：∠ABC＝∠ACQ；
（2）∠ABC＝∠ACQ，
理由如下：∵AB＝BC，
∴∠BAC＝，
∵AP＝PQ，
∴∠PAQ＝，
∵∠APQ＝∠ABC，
∴∠BAC＝∠PAQ，
∴△BAC∽△PAQ，
∴，
∵∠BAP+∠PAC＝∠PAC+∠CAQ，
∴∠BAP＝∠CAQ，
∴△BAP∽△CAQ，
∴∠ABC＝∠ACQ；
（3）如图3，连接AB，
∵四边形ADBC和四边形APEF都是正方形，
∴AB＝AC，AP＝AQ，∠BAC＝∠PAQ＝45°，
∴∠BAP＝∠CAQ，，
∴△BAP∽△CAQ，
∴，
∴BP＝CQ＝2，
∵AP2＝AC2+PC2，
∴100＝AC2+（AC﹣2）2，
∴AC＝8，AC＝﹣6（舍去），
∴正方形ADBC的边长为8．
【点评】本题是四边形综合题，考查了正方形的性质，等边三角形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理等知识，灵活运用这些性质解决问题是解题的关键．题目
测量小河的宽度（AB的长）
测量目标示意图

相关数据
BC＝1.5m，DE＝2m，BD＝4m．