辽宁省大连市瓦房店市2023-2024学年八年级上册期中数学试题（含解析）

这是一份辽宁省大连市瓦房店市2023-2024学年八年级上册期中数学试题（含解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（将唯一正确答案的代号填在答题卡中，每小题2分，共20分）
1．平面直角坐标系中,,则点关于y轴对称的点的坐标为（ ）
A．B．C．D．
2．已知一个三角形的两边长分别为8和2，则这个三角形的第三边长可能是（ ）
A．4B．6C．8D．10
3．下列四个图案中，不是轴对称图案的是（ ）
A． B．
C． D．
4．已知直角三角形中30°角所对的直角边为2cm，则斜边的长为（ ）
A．2cmB．4cmC．6cmD．8cm
5．下列条件中，能判定△ABC≌△DEF的是（ ）
A．∠A＝∠D，∠B＝∠E，∠C＝∠FB．AC＝DF，∠B＝∠E，BC＝EF
C．AB＝DE，∠B＝∠E，AC＝DFD．AB＝DE，∠B＝∠E，BC＝EF
6．若一个多边形的内角和等于 1440°，则这个多边形是（ ）
A．四边形B．六边形C．八边形D．十边形
7．如图，AE平分∠BAC，DE∥AB，若AD=5，则DE等于（ ）
A．2B．3C．4D．5
8．如图，在中，是的垂直平分线，且分别交、于点D和E，，，则为（ ）
A．B．C．D．
9．如图，是的中线，是的中线，，则（ ）
A．1B．2C．3D．4
10．如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E，若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（ ）
A．16cmB．19cmC．22cmD．25cm
二、填空题（本大题共6个小题，每小题3分，共18分）
11．为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条这样做的道理是 .
12．如图，在△ABC中，AB=AC，∠A=40°，则外角∠ACD= 度．
13．如图，等腰三角形中，，，于D，则等于 ．
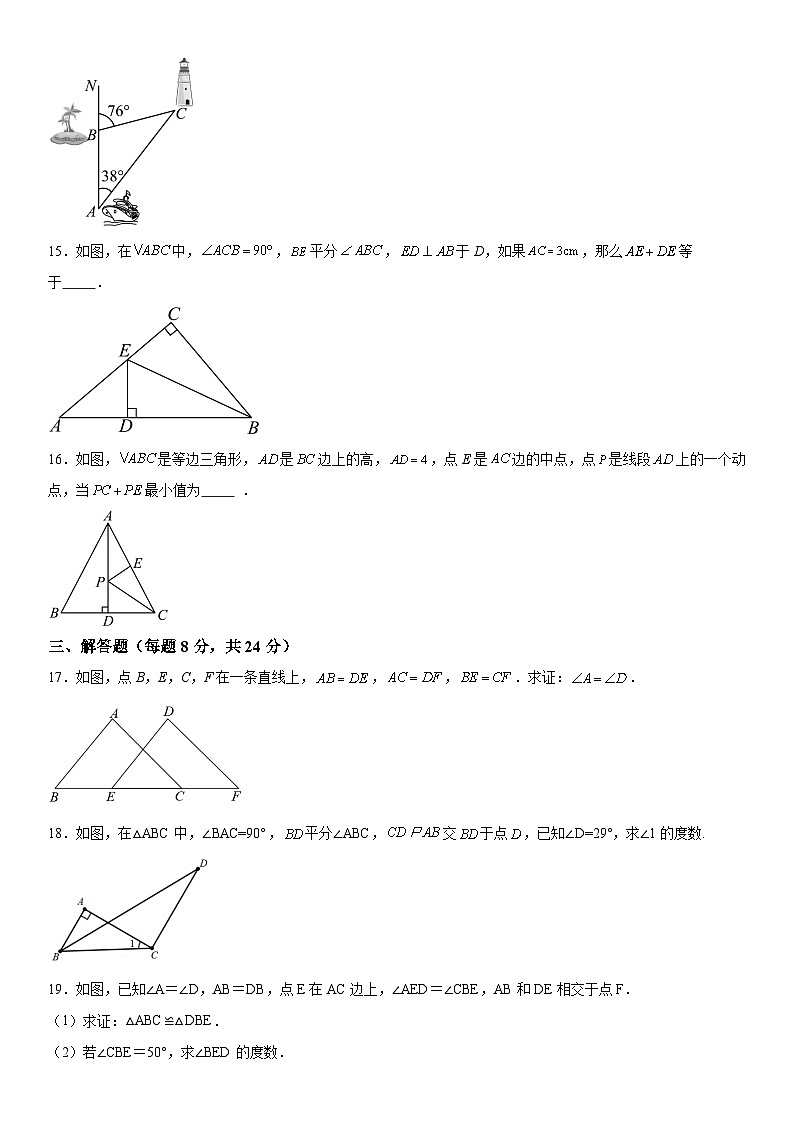
14．如图，上午8时，一条船从海岛A出发，以16nmile/h的速度向正北航行，10时到达海岛B处，从海岛A，B处望灯塔C，分别测得，，则海岛B与灯塔C之间的距离是 nmile．

15．如图，在中，，平分，于D，如果，那么等于 ．
16．如图，是等边三角形，是边上的高，，点E是边的中点，点是线段上的一个动点，当最小值为 ．

三、解答题（每题8分，共24分）
17．如图，点B，E，C，F在一条直线上，，，．求证：．
18．如图，在△ABC中，∠BAC=90°，平分∠ABC，交于点，已知∠D=29°，求∠1的度数.
19．如图，已知∠A＝∠D，AB＝DB，点E在AC边上，∠AED＝∠CBE，AB和DE相交于点F．
（1）求证：△ABC≌△DBE．
（2）若∠CBE＝50°，求∠BED的度数．
四、解答题（每题8分，共16分）
20．如图，的三个顶点在边长为1的正方形网格中，已知，，．
(1)画出及关于y轴对称的；
(2)写出点A的对应点的坐标是______，点B的对应点的坐标是______，点C的对应点的坐标是______．
(3)请直接写出以为边且与全等的三角形的第三个顶点（不与C重合）的坐标．
21．如图，是的边上的高，点E为上一点，且．
(1)试说明；
(2)若，求的面积．
五、解答题（本题8分）
22．如图，是边长为的等边三角形，，点Q为射线边上一点，当的长为多少时，是直角三角形.

六、解答题（本题10分）
23．如图，是等边三角形，是中线，延长至点E，使．
(1)求证：；
(2)过点D作垂直于，垂足为F，若，求的周长．
七、解答题（本题12分）
24．已知，与都是等腰直角三角形，，，，如图，连接、．

(1)如图1，求证：；
(2)如图2，点D在内，B、D、E三点在同一直线上．
①过点A作的高，证明：；
②如图3，若平分，交于点G，，求的长．
八、（本题12分）
25．综合与实践
（1）我们在第十二章《全等三角形》中学习了全等三角形的性所和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题.例如：我们在解决：“如下图，在中，，，线段DE经过点C，且于点D，于点E.求证：，”这个问题时，只要证明____________，即可得到解决：（填空，不需证明）

类比应用
（2）如下图，在平面直角坐标系中，点A、C分别在y轴和x轴上，点A坐标为，点，若是等腰直角三角形，，，求点B的坐标.

拓展提升
（3）如下图，平面直角坐标系中，若是等腰直角三角形，，；点D是第一象限上方一点，且，连接．

①求的度数；
②若长为4，求四边形的面积.
参考答案与解析
1．C
【分析】本题考查关于坐标轴对称的知识．根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变即可得到本题答案．
【详解】解:点关于y轴对称的点的坐标是．
故选:C．
2．C
【分析】根据在三角形中任意两边之和＞第三边，任意两边之差＜第三边；可求第三边长的范围，再选出答案．
【详解】设第三边长为xcm，
则8﹣2＜x＜2+8，
6＜x＜10，
故选C．
【点睛】本题考查了三角形三边关系，解题的关键是根据三角形三边关系定理列出不等式，然后解不等式即可．
3．C
【分析】根据轴对称的概念对各选项分析判断利用排除法求解．
【详解】解：A．此图案是轴对称图形，不符合题意；
B．此图案是轴对称图形，不符合题意；
C．此图案不是轴对称图形，符合题意；
D．此图案是轴对称图形，不符合题意；
故选：C．
【点睛】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
4．B
【分析】根据在直角三角形中，30°角所对的直角边等于斜边的一半即可求解．
【详解】解：由题意可知，在直角三角形中，30°角所对的直角边等于斜边的一半，
所以斜边=2×2=4cm
故选B．
【点睛】题目主要考查在直角三角形中，30°角所对的直角边等于斜边的一半，熟练掌握运用此定理是解题关键．
5．D
【分析】根据全等三角形的判定定理进行判断．
【详解】
A. 没有边的参与，不能判定△ABC≌△DEF，故本选项错误；
B. 根据SSA不能判定△ABC≌△DEF，故本选项错误；
C. 根据SSA不能判定△ABC≌△DEF，故本选项错误；
D. 由全等三角形的判定定理SAS可以证得△ABC≌△DEF.故本选项正确；
故答案选：D.
【点睛】本题考查了全等三角形的判定，解题的关键是熟练的掌握全等三角形的判定与性质.
6．D
【分析】根据多边形内角和公式(n-2) 180°,设多边形边数为n,再列方程(n-2) 180°=1440°,解方程即可.
【详解】解:设多边形边数为n,由题意得:
(n-2) 180°=1440°,
解得:n=10.
所以D选项是正确的.
【点睛】此题主要考查了多边形内角,关键是掌握多边形内角和定理:(n-2)·180°(n≥3，且n为整数).
7．D
【分析】由角平分线的定义和平行线的性质易得DE=5.
【详解】∵AE平分∠BAC，
∴∠EAC=∠EAB，
∵DE∥AB，
∴∠DEA=∠BAE，
∴∠DEA=∠DAE，
∴DE=AD=5.
故选D.
【点睛】本题考查的是平行线的性质、角平分线的性质以及等腰三角形的判定，用到的知识点为：两直线平行，内错角相等；等角对等边.
8．A
【分析】本题考查了三角形内角和定理，垂直平分线的性质，等腰三角形的性质．由三角形内角和等于180度，求得，再根据垂直平分线的性质，得到，进而得到，即可求出的度数．熟练掌握垂直平分线上的点到线段两端距离相等是解题关键．
【详解】解：，，
，
是的垂直平分线，
，
，
，
故选：A．
9．B
【分析】本题主要考查三角形的中线与面积的关系，解题的关键是熟练掌握三角形的中线把三角形的面积平均分成相等的两部分；由题意易得，，，然后问题可求解．
【详解】解：∵是的中线，
∴，
∵是的中线，
∴，，
∵，
∴；
故选B．
10．B
【分析】根据作法可知MN是AC的垂直平分线，利用垂直平分线的性质进行求解即可得答案．
【详解】解：根据作法可知MN是AC的垂直平分线，
∴DE垂直平分线段AC，
∴DA=DC，AE=EC=6cm，
∵AB+AD+BD=13cm，
∴AB+BD+DC=13cm，
∴△ABC的周长=AB+BD+BC+AC=13+6=19cm，
故选B．
【点睛】本题考查作图-基本作图，线段的垂直平分线的性质等知识，解题的关键是熟练掌握线段的垂直平分线的性质．
11．三角形的稳定性
【分析】根据三角形的稳定性分析，即可求解．
【详解】解：木工师傅在木门的背面加钉了一根木条这样做的道理是利用三角形的稳定性．
故答案为：三角形的稳定性．
【点睛】本题考查了三角形的稳定性，熟练掌握三角形的稳定性是解题的关键．
12．110
【分析】根据等腰三角形的性质得到∠B=∠ACB，根据三角形的内角和定理求出∠ACB，∠根据三角形的外角性质即可求出答案．
【详解】∵AB=AC，
∴∠B=∠ACB，
∵∠A=40°，
∴∠B=∠ACB=（180°-∠A）=70°，
∴∠BCD=∠A+∠B=40°+70°=110°，
故答案为110．
【点睛】本题主要考查对等腰三角形的性质，三角形的内角和定理，三角形的外角性质等知识点的理解和掌握，能求出∠B的度数是解此题的关键．
13．##23度
【分析】本题主要考查等腰三角形的性质及直角三角形的性质，熟练掌握等腰三角形的性质是解题的关键；由题意易得，然后问题可求解．
【详解】解：∵在等腰三角形中，，，
∴，
∵，
∴，
∴；
故答案为：．
14．32
【分析】根据路程=速度×时间即可求出AB，然后根据三角形外角的性质求出∠C，再利用等角对等边即可得出结论．
【详解】解：由题意可知：AB=16×（10－8）=32 nmile
∵，
∴∠C=∠NBC－∠BAC=38°
∴∠C =∠BAC
∴BC=AB=32 nmile
故答案为：32．
【点睛】此题考查的是三角形外角的性质和等腰三角形的判定，掌握三角形外角的性质和等角对等边是解题关键．
15．##3厘米
【分析】本题考查了角平分线的性质定理．根据角平分线上的点到角两边的距离相等，得到，即可求出答案．
【详解】解：平分，，，
，
，
故答案为：．
16．4
【分析】本题考查了最短路径问题及等边三角形的性质，理解“两点之间线段最短”是解题的关键．先根据“两点之间线段最短”找到最小值，再根据等边三角形的性质进行求解．
【详解】解：如图：

∵是等边三角形，是边上的高，
∴，
∴B、关于直线对称，
，
∵是等边三角形，为的中点，
，
故答案为：4．
17．见解析
【分析】根据得到，然后证明，即可得出结论．
【详解】证明：∵，
∴，
在和中，
，
∴．
∴．
【点睛】本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定定理以及性质定理是解本题的关键．
18．32°
【分析】先根据平行线的性质求出∠2的度数，再根据角平分线的性质得到∠ABC的度数，由三角形内角和为180度，得出∠1的度数.
【详解】解：∵CD∥AB,∠D=29°，
∴∠2=∠D =29°.
又∵平分∠ABC，
∴∠ABC=2∠2 =58°.
∵CD∥AB,∠BAC=90°
∴∠3=∠BAC=90°，∠ABC+∠BCD=180°
∴∠BCD=180°-∠ABC=122°
∴∠1=∠BCD-∠3=122°-90°=32°.
【点睛】考查了平行线的性质，解题关键是由平行线的性质求得∠ABD的度数，从而得出∠ABC的度数，再根据三角形内角和定理求解.
19．（1）见解析；（2）∠BEC=65°
【分析】（1）根据三角形的内角和得到∠ABD＝∠AED，求得∠ABC＝∠DBE，根据全等三角形的判定定理即可得到结论；
（2）根据全等三角形的性质得到BE＝BC，求得∠BEC＝∠C，根据三角形的内角和即可得到结论．
【详解】（1）证明：∵∠A＝∠D，∠AFE＝∠BFD，
∴∠ABD＝∠AED，
又∵∠AED＝∠CBE，

∴∠ABD+∠ABE＝∠CBE+∠ABE，
即∠ABC＝∠DBE，
在△ABC和△DBE中，
，
∴△ABC≌△DBE（ASA）；
（2）解：∵△ABC≌△DBE，
∴BE＝BC，
∴∠BEC＝∠C，
∵∠CBE＝50°，
∴∠BEC＝∠C＝65°．
【点睛】本题考查了全等三角形的判定和性质，灵活的根据题中已知条件选择合适的判定方法是解题的关键.
20．(1)图见详解
(2)，，
(3)第三个顶点的坐标为，或
【分析】本题主要考查了运用轴对称变换进行作图、全等三角形的性质以及坐标确定位置的运用，解决问题的关键是掌握画一个图形的轴对称图形的方法，画图时先从确定一些特殊的对称点开始．
（1）根据各点坐标画出三角形即可，再根据轴对称的性质，画出三角形即可；
（2）根据各顶点的位置写出其坐标即可；
（3）根据以为公共边且与全等的三角形的第三个顶点的位置，写出其坐标即可．
【详解】（1）解：所作和如图所示：

（2）解：由图可得，点的坐标是，点的坐标是，点的坐标是；
（3）解：为公共边，
与全等的三角形的第三个顶点的坐标为，或．
21．(1)见解析
(2)
【分析】（1）利用判断出，根据全等三角形的性质即可得出结论；
（2）由全等三角形的性质得出，求出和的长，则可求出答案．
【详解】（1）∵为边上的高．
∴，
∴，
在和中，
∴，
∴；
（2）∵，
∴，
∵，
∴，
∴，
∴的面积．
【点睛】此题主要考查了全等三角形的判定与性质、三角形的面积，掌握全等三角形的判定定理是解本题的关键．
22．或
【分析】本题考查了等边三角形的性质、含角的直角三角形等知识点，掌握分类讨论的数学思想是解题关键．
【详解】解：当时，如图1所示：
∵是边长为的等边三角形，
∴，
∵，
∴
∴；
当时，如图2所示：
则，
∴，
∴；
综上所述，当或时，是直角三角形
23．(1)证明见解析
(2)
【分析】（1）等边三角形三线合一，得到，等边对等角结合三角形的外角，推出，进而得到，即可；
（2）易得是含30度角的直角三角形，进而得到，中线得到，求出的长，即可．
【详解】（1）证明：∵是等边三角形，是中线，
∴，．
∵，
∴．
又∵，
∴．
∴．
∴．
（2）∵，
∴
∴在中，．
∴．
∵，
∴．
∴．
【点睛】本题考查等边三角形的性质，等腰三角形的判定和性质，三角形的外角，含30度角的直角三角形．熟练掌握三线合一，等边对等角，等角对等边，以及30度的角所对的直角边是斜边的一半，是解题的关键．
24．(1)证明见解析
(2)①证明见解析；②
【分析】（1）根据“”易证，即可证明结论；
（2）①由（1）知：，根据等腰三角形三线合一的性质可知，点是的中点，再根据直角三角形斜边中线等于斜边一半，得到，即可证明结论；
②延长A交于点K，利用等腰直角三角形的性质和角平分线的定义，易证，得到，再根据三角形外角的性质，得到，从而证明，得到，即可得到答案．
【详解】（1）证明：，
，
，
在和中，
，
，
；
（2）证明：①由（1）知：，
，，
点是的中点，
，
，即，
B，D，E三点在同一直线上，
；
②解：如图，延长A交于点K，
是等腰直角三角形，
，
，
，
，
是平分线，
，
在和中，
，
，
，
，
，
，
在和中，
，
．

【点睛】本题考查了全等三角形的判定和性质，等腰三角形的判定和性质，直角三角形的特征，三角形外角的性质等知道，作辅助线构造全等三角形，掌握全等三角形的判定和性质是解题关键．
25．（1），；（2）；（3）①；②8
【分析】（1）证明，可得结论；
（2）过点作轴垂线，垂足为，证明，由全等三角形的性质得出，，
（3）①过点作于点，，交的延长线于点，证明，由全等三角形的性质得出，得出；
②由全等三角形的性质及等腰直角三角形的性质可得出答案．
【详解】解：（1），，
又，
，
在和中，
，
∴，
，；
故答案为：，；
（2）过点作轴垂线，垂足为，
由题意知：，，，，
，，
，
在和中，
，
∴，
，，
，
故点坐标为；
（3）①过点作于点，，交的延长线于点，
，
，
，
，
，，
∴，
，
，，
平分，
；
②∵，
，
，
由①可知，，
和都是等腰直角三角形，
．
【点睛】本题是三角形综合题，考查全等三角形的判定与性质，坐标与图形的性质，角平分线的性质，直角三角形的性质，解题的关键是利用数形结合的思想，找出所求问题需要的关系，通过三角形的全等可以得到相关的角和边之间的关系．