广东省深圳市深圳外国语学校学校2023-2024学年上学期九年级第3次月考数学试卷（12月）

这是一份广东省深圳市深圳外国语学校学校2023-2024学年上学期九年级第3次月考数学试卷（12月），共22页。试卷主要包含了下列说法正确的是，已知二次函数y＝ax2﹣2x+等内容，欢迎下载使用。

一．选择题（每题3分，共30分）
1．一元二次方程x2+3x＝0的解是（ ）
A．x＝﹣3 B．x1＝0，x2＝3 C．x1＝0，x2＝﹣3 D．x＝3
2．下列函数中，y的值随x值的增大而减小的是（ ）
A．y＝x2+1B．y＝﹣x2+1C．y＝2x+1D．y＝﹣2x+1
3．下列说法正确的是（ ）
A．经过三点可以作一个圆
B．三角形的外心到这个三角形的三边距离相等
C．同圆或等圆中，等弧所对的圆心角相等
D．相等的圆心角所对的弧相等
4．在△ABC中，∠A，∠B都是锐角，且sinA＝，csB＝，则△ABC的形状是（ ）
A．直角三角形B．钝角三角形
C．锐角三角形D．不能确定
5．已知⊙O的半径为10cm，点P到圆心O的距离为11cm，则点P和⊙O的位置关系是（ ）
A．点P在圆内B．点P在圆上C．点P在圆外D．不能确定
6．在平面直角坐标系中，将抛物线y＝x2平移，可以得到抛物线y＝x2+2x+1，下列平移的叙述正确的是（ ）
A．向上平移1个单位长度
B．向下平移1个单位长度
C．向左平移1个单位长度
D．向右平移1个单位长度
7．如图，有一个半径为2的圆形时钟，其中每个相邻刻度间的弧长均相等，过9点和11点的位置作一条线段，则钟面中阴影部分的面积为（ ）
A．π﹣B．π﹣C．π﹣2D．π﹣
8．已知二次函数y＝ax2﹣2x+（a为常数，且a＞0），下列结论：①函数图象一定经过第一、二、四象限；②函数图象一定不经过第三象限；③当x＜0时，y随x的增大而减小；④当x＞0时，y随x的增大而增大．其中所有正确结论的序号是（ ）
A．①②B．②③C．②D．③④
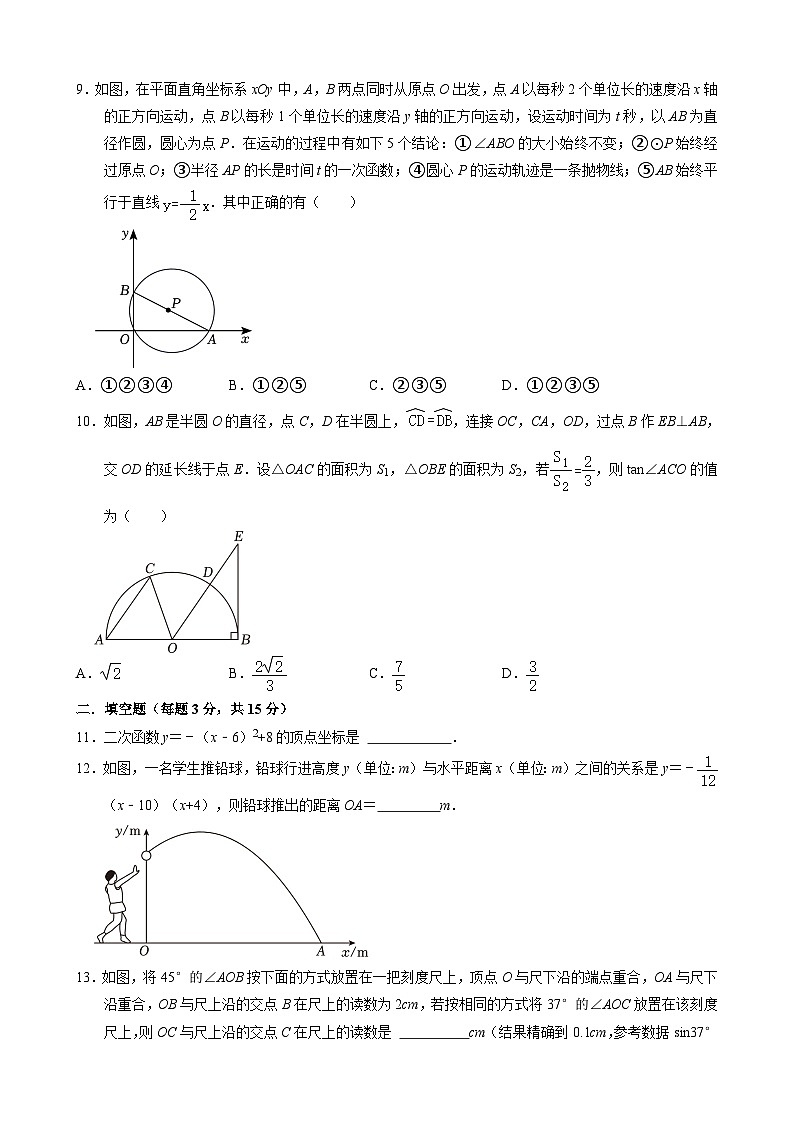
9．如图，在平面直角坐标系xOy中，A，B两点同时从原点O出发，点A以每秒2个单位长的速度沿x轴的正方向运动，点B以每秒1个单位长的速度沿y轴的正方向运动，设运动时间为t秒，以AB为直径作圆，圆心为点P．在运动的过程中有如下5个结论：①∠ABO的大小始终不变；②⊙P始终经过原点O；③半径AP的长是时间t的一次函数；④圆心P的运动轨迹是一条抛物线；⑤AB始终平行于直线．其中正确的有（ ）
A．①②③④B．①②⑤C．②③⑤D．①②③⑤
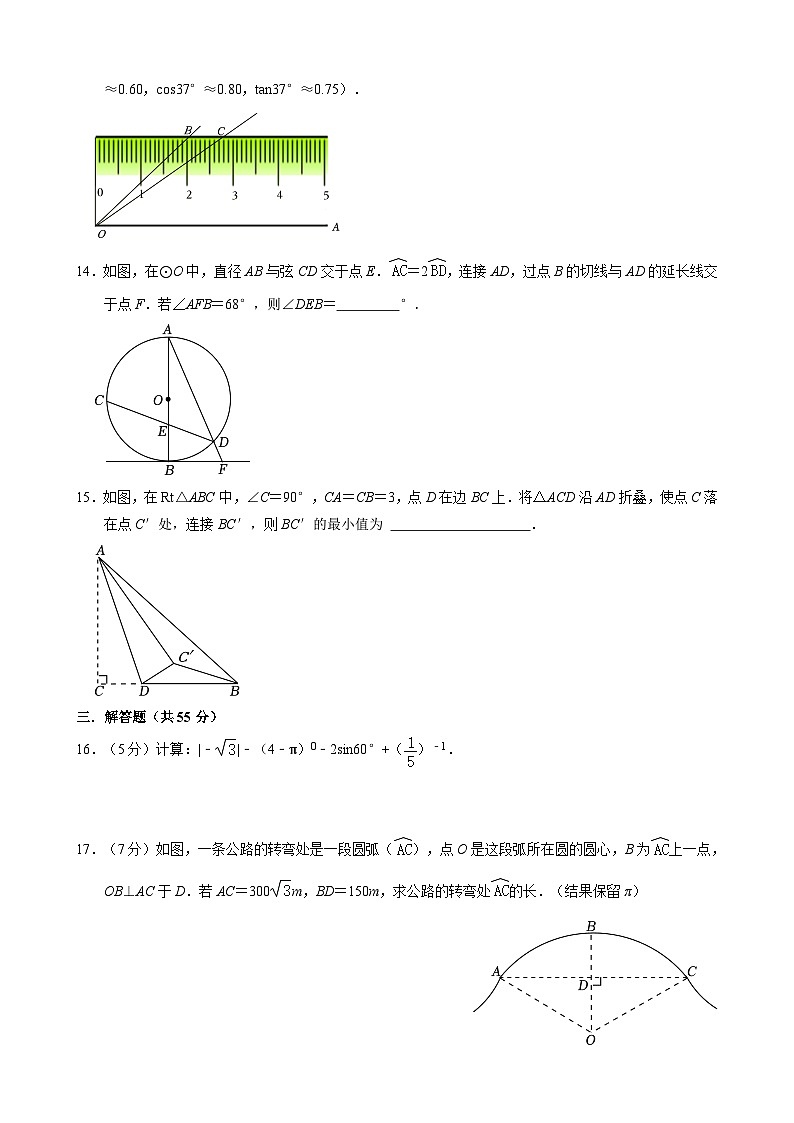
10．如图，AB是半圆O的直径，点C，D在半圆上，，连接OC，CA，OD，过点B作EB⊥AB，交OD的延长线于点E．设△OAC的面积为S1，△OBE的面积为S2，若，则tan∠ACO的值为（ ）
A．B．C．D．
二．填空题（每题3分，共15分）
11．二次函数y＝﹣（x﹣6）2+8的顶点坐标是 ．
12．如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是y＝﹣（x﹣10）（x+4），则铅球推出的距离OA＝ m．
13．如图，将45°的∠AOB按下面的方式放置在一把刻度尺上，顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数为2cm，若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数是 cm（结果精确到0.1cm，参考数据sin37°≈0.60，cs37°≈0.80，tan37°≈0.75）．
14．如图，在⊙O中，直径AB与弦CD交于点E．＝2，连接AD，过点B的切线与AD的延长线交于点F．若∠AFB＝68°，则∠DEB＝ °．
15．如图，在Rt△ABC中，∠C＝90°，CA＝CB＝3，点D在边BC上．将△ACD沿AD折叠，使点C落在点C′处，连接BC′，则BC′的最小值为 ．
三．解答题（共55分）
16．（5分）计算：|﹣|﹣（4﹣π）0﹣2sin60°+（）﹣1．
17．（7分）如图，一条公路的转弯处是一段圆弧（），点O是这段弧所在圆的圆心，B为上一点，OB⊥AC于D．若AC＝300m，BD＝150m，求公路的转弯处的长．（结果保留π）
18．（7分）四边形不具有稳定性，工程上可利用这一性质解决问题．如图是某篮球架的侧面示意图，BE，CD，GF为长度固定的支架，支架在A，D，G处与立柱AH连接（AH垂直于MN，垂足为H），在B，C处与篮板连接（BC所在直线垂直于MN），EF是可以调节长度的伸缩臂（旋转点F处的螺栓改变EF的长度，使得支架BE绕点A旋转，从而改变四边形ABCD的形状，以此调节篮板的高度）．已知AD＝BC，DH＝208cm，测得∠GAE＝60°时，点C离地面的高度为288cm．调节伸缩臂EF，将∠GAE由60°调节为54°，判断点C离地面的高度升高还是降低了？升高（或降低）了多少？（参考数据：sin54°≈0.8，cs54°≈0.6）
19．（8分）用各种盛水容器可以制作精致的家用流水景观（如图1）．
科学原理：如图2，始终盛满水的圆柱体水桶水面离地面的高度为H（单位：cm），如果在离水面竖直距离为h（单位：cm）的地方开大小合适的小孔，那么从小孔射出水的射程（水流落地点离小孔的水平距离）s（单位：cm）与h的关系式为s2＝4h（H﹣h）．
应用思考：现用高度为20cm的圆柱体塑料水瓶做相关研究，水瓶直立地面，通过连续注水保证它始终盛满水，在离水面竖直距离hcm处开一个小孔．
（1）写出s2与h的关系式；并求出当h为何值时，射程s有最大值，最大射程是多少？
（2）在侧面开两个小孔，这两个小孔离水面的竖直距离分别为a，b，要使两孔射出水的射程相同，求a，b之间的关系式；
（3）如果想通过垫高塑料水瓶，使射出水的最大射程增加16cm，求垫高的高度及小孔离水面的竖直距离．
20．（8分）如图，AB为⊙O的弦，OC⊥OA交AB于点P，交过点B的直线于点C，且CB＝CP．
（1）试判断直线BC与⊙O的位置关系，并说明理由；
（2）若sinA＝，OA＝8，求CB的长．
21．（8分）【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积？
【初步尝试】如图1，已知扇形OAB，请你用圆规和无刻度的直尺过圆心O作一条直线，使扇形的面积被这条直线平分；
【问题联想】如图2，已知线段MN，请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP；
【问题再解】如图3，已知扇形OAB，请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧，使扇形的面积被这条圆弧平分．
（友情提醒：以上作图均不写作法，但需保留作图痕迹）
22．（12分）已知：A、B为圆上两定点，点C在该圆上，∠C为所对的圆周角．
知识回顾
（1）如图①，⊙O中，B、C位于直线AO异侧，∠AOB+∠C＝135°．
①求∠C的度数；
②若⊙O的半径为5，AC＝8，求BC的长；
逆向思考
（2）如图②，若P为圆内一点，且∠APB＜120°，PA＝PB，∠APB＝2∠C．求证：P为该圆的圆心；
拓展应用
（3）如图③，在（2）的条件下，若∠APB＝90°，点C在⊙P位于直线AP上方部分的圆弧上运动．点D在⊙P上，满足CD＝CB﹣CA的所有点D中，必有一个点的位置始终不变．请证明．
参考答案与试题解析
一．选择题（共10小题）
1．一元二次方程x2+3x＝0的解是（ ）
A．x＝﹣3B．x1＝0，x2＝3
C．x1＝0，x2＝﹣3D．x＝3
【解答】解：x2+3x＝0，
x（x+3）＝0，
x＝0，x+3＝0，
x1＝0，x2＝﹣3，
故选：C．
2．下列函数中，y的值随x值的增大而减小的是（ ）
A．y＝x2+1B．y＝﹣x2+1C．y＝2x+1D．y＝﹣2x+1
【解答】解：选项A中，函数y＝x2+1，x＜0时，y随x的增大而减小；故A不符合题意；
选项B中，函数y＝﹣x2+1，x＞0时，y随x的增大而减小；故B不符合题意；
选项C中，函数y＝2x+1，y随x的增大而增大；故C不符合题意；
选项D中，函数y＝﹣2x+1，y随x的增大而减小．故D符合题意；
故选：D．
3．下列说法正确的是（ ）
A．经过三点可以作一个圆
B．三角形的外心到这个三角形的三边距离相等
C．同圆或等圆中，等弧所对的圆心角相等
D．相等的圆心角所对的弧相等
【解答】解：A、经过不在同一条直线上的三点可确定一个圆，故A错误；B、三角形的外心到这个三角形的三个顶点的距离相等，故B错误；
C、同圆或等圆中，等弧所对的圆心角相等，故C正确；D、同圆或等圆中，相等的圆心角所对的弧相等，故D错误．故选：C．
4．在△ABC中，∠A，∠B都是锐角，且sinA＝，csB＝，则△ABC的形状是（ ）
A．直角三角形B．钝角三角形
C．锐角三角形D．不能确定
【解答】解：∵csB＝，
∴∠B＝30°，
∵sinA＝，
∴∠A＝30°，
∵∠A+∠B+∠C＝180°，
∴∠C＝180°﹣30°﹣30°＝120°，
∴△ABC是钝角三角形，
故选：B．
5．已知⊙O的半径为10cm，点P到圆心O的距离为12cm，则点P和⊙O的位置关系是（ ）
A．点P在圆内B．点P在圆上C．点P在圆外D．不能确定
【解答】解：∵⊙O的半径r＝10cm，点P到圆心O的距离OP＝12cm，
∴OP＞r，
∴点P在⊙O外，
故选：C．
6．在平面直角坐标系中，将抛物线y＝x2平移，可以得到抛物线y＝x2+2x+1，下列平移的叙述正确的是（ ）
A．向上平移1个单位长度
B．向下平移1个单位长度
C．向左平移1个单位长度
D．向右平移1个单位长度
【解答】解：∵y＝x2+2x+1＝（x+1）2，
∴平移后抛物线的顶点为（﹣1，0），
抛物线y＝x2的顶点为（0，0），
∴点（0，0）向左平移1个单位得点（﹣1，0），
∴抛物线y＝x2向左平移1个单位可得抛物线y＝x2+2x+1，
故选：C．
7．如图，有一个半径为2的圆形时钟，其中每个相邻刻度间的弧长均相等，过9点和11点的位置作一条线段，则钟面中阴影部分的面积为（ ）
A．π﹣B．π﹣C．π﹣2D．π﹣
【解答】解：连接OA、OB，过点O作OC⊥AB，
由题意可知：∠AOB＝60°，
∵OA＝OB，
∴△AOB为等边三角形，
∴AB＝AO＝BO＝2
∴S扇形AOB＝＝π，
∵OC⊥AB，
∴∠OCA＝90°，AC＝1，
∴OC＝，
∴S△AOB＝＝，
∴阴影部分的面积为：π﹣；
故选：B．
8．已知二次函数y＝ax2﹣2x+（a为常数，且a＞0），下列结论：①函数图象一定经过第一、二、四象限；②函数图象一定不经过第三象限；③当x＜0时，y随x的增大而减小；④当x＞0时，y随x的增大而增大．其中所有正确结论的序号是（ ）
A．①②B．②③C．②D．③④
【解答】解：∵a＞0时，抛物线开口向上，
∴对称轴为直线x＝＝＞0，
当x＜0时，y随x的增大而减小，
当x＞时，y随x的增大而增大，
∴函数图象一定不经过第三象限，函数图象可能经过第一、二、四象限．
故选：B．
9．如图，在平面直角坐标系xOy中，A，B两点同时从原点O出发，点A以每秒2个单位长的速度沿x轴的正方向运动，点B以每秒1个单位长的速度沿y轴的正方向运动，设运动时间为t秒，以AB为直径作圆，圆心为点P．在运动的过程中有如下5个结论：
①∠ABO的大小始终不变；
②⊙P始终经过原点O；
③半径AP的长是时间t的一次函数；
④圆心P的运动轨迹是一条抛物线；
⑤AB始终平行于直线．
其中正确的有（ ）
A．①②③④B．①②⑤C．②③⑤D．①②③⑤
【解答】解：①由题意得：OA＝2t，OB＝t，
则tan∠ABO＝，
∴∠ABO的大小始终不变，正确；
②∵AB是圆P的直径，
则AB所对的圆周角为90°，即∠AOB＝90°，
∴⊙P始终经过原点O，正确；
③由点A、B的坐标，根据中点坐标公式得：点P（t，t），
则AP＝＝t，
即AP的长度是时间t的一次函数，正确；
④由③知，点P（t，t），
则点P在直线y＝x上，故④错误；
⑤设直线AB的表达式为：y＝kx+b，
则，解得：，
故直线AB的表达式为：y＝﹣x+t，
∵AB始终平行于直线，正确，
故选：D．
10．如图，AB是半圆O的直径，点C，D在半圆上，，连接OC，CA，OD，过点B作EB⊥AB，交OD的延长线于点E．设△OAC的面积为S1，△OBE的面积为S2，若，则tan∠ACO的值为（ ）
A．B．C．D．
【解答】解：如图，过C作CH⊥AO于H，
∵，
∴∠COD＝∠BOE＝∠CAO，
∵，即，
∴，
∵∠A＝∠BOE，
∴tan∠A＝tan∠BOE，
∴，即，
设AH＝2m，则BO＝3m＝AO＝CO，
∴OH＝3m﹣2m＝m，
∴CH＝，
∴tan∠A＝＝，
∵OA＝OC，
∴∠A＝∠ACO，
∴tan∠ACO＝；
故选A．
二．填空题（共5小题）
11．二次函数y＝﹣（x﹣6）2+8的顶点坐标是 （6，8） ．
【解答】解：二次函数y＝﹣（x﹣6）2+8的图象的顶点坐标是（6，8）．
故答案为：（6，8）．
12．如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是y＝﹣（x﹣10）（x+4），则铅球推出的距离OA＝ 10 m．
【解答】解：令y＝0，则﹣（x﹣10）（x+4）＝0，
解得：x＝10或x＝﹣4（不合题意，舍去），
∴A（10，0），
∴OA＝10m．
故答案为：10．
13．如图，将45°的∠AOB按下面的方式放置在一把刻度尺上，顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数为2cm，若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数是 2.7 cm（结果精确到0.1cm，参考数据sin37°≈0.60，cs37°≈0.80，tan37°≈0.75）．
【解答】解：如图，过点B作BD⊥OA于D，过点C作CE⊥OA于E，
在△BOD中，∠BDO＝90°，∠DOB＝45°，
∴CE＝BD＝2cm，
在△OCE中，∠COE＝37°，∠CEO＝90°，
∴tan37°＝，
∴OE＝2.7cm，
即OC与尺上沿的交点C在尺上的读数是2.7cm．
故答案为：2.7．
14．如图，在⊙O中，直径AB与弦CD交于点E．＝2，连接AD，过点B的切线与AD的延长线交于点F．若∠AFB＝68°，则∠DEB＝ 66 °．
【解答】解：如图，连接OC，OD，
∵BF是⊙O的切线，AB是⊙O的直径，
∴OB⊥BF，
∴∠ABF＝90°，
∵∠AFB＝68°，
∴∠BAF＝90°﹣∠AFB＝22°，
∴∠BOD＝2∠BAF＝44°，
∵，
∴∠COA＝2∠BOD＝88°，
∴∠CDA＝，
∵∠DEB是△AED的一个外角，
∴∠DEB＝∠BAF+∠CDA＝66°，
故答案为：66．
15．如图，在Rt△ABC中，∠C＝90°，CA＝CB＝3，点D在边BC上．将△ACD沿AD折叠，使点C落在点C′处，连接BC′，则BC′的最小值为 ．
【解答】解：∵∠C＝90°，CA＝CB＝3，
∴，
由折叠的性质可知AC＝AC'＝3，
∵BC'≥AB﹣AC'，
∴当A、C′、B三点在同一条直线时，BC'取最小值，最小值即为，
故答案为 ．
三．解答题（共7小题）
16．计算：|﹣|﹣（4﹣π）0﹣2sin60°+（）﹣1．
【解答】解：|﹣|﹣（4﹣π）0﹣2sin60°+（）﹣1
＝﹣1﹣2×+5
＝﹣1﹣+5
＝4．
17．如图，一条公路的转弯处是一段圆弧（），点O是这段弧所在圆的圆心，B为上一点，OB⊥AC于D．若AC＝300m，BD＝150m，求公路的转弯处的长．（结果保留π）
【解答】解：∵OB⊥AC，
∴AD＝ AC＝150m，∠AOC＝2∠AOB，
在Rt△AOD中，
∵AD2+OD2＝OA2，OA＝OB，
∴AD2+（OA﹣BD）2＝OA2，
∴+（OA﹣150）2＝OA2，
解得：OA＝300m，
∴sin∠AOB＝＝，
∴∠AOB＝60°，
∴∠AOC＝120°，
∴的长＝＝200πm．
18．四边形不具有稳定性，工程上可利用这一性质解决问题．如图是某篮球架的侧面示意图，BE，CD，GF为长度固定的支架，支架在A，D，G处与立柱AH连接（AH垂直于MN，垂足为H），在B，C处与篮板连接（BC所在直线垂直于MN），EF是可以调节长度的伸缩臂（旋转点F处的螺栓改变EF的长度，使得支架BE绕点A旋转，从而改变四边形ABCD的形状，以此调节篮板的高度）．已知AD＝BC，DH＝208cm，测得∠GAE＝60°时，点C离地面的高度为288cm．调节伸缩臂EF，将∠GAE由60°调节为54°，判断点C离地面的高度升高还是降低了？升高（或降低）了多少？（参考数据：sin54°≈0.8，cs54°≈0.6）
【解答】解：点C离地面的高度升高了，
理由：如图，当∠GAE＝60°时，过点C作CK⊥HA，交HA的延长线于点K，
∵BC⊥MN，AH⊥MN，
∴BC∥AH，
∵AD＝BC，
∴四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ADC＝∠GAE＝60°，
∵点C离地面的高度为288cm，DH＝208cm，
∴DK＝288﹣208＝80（cm），
在Rt△CDK中，CD＝＝＝160（cm），
如图，当∠GAE＝54°，过点C作CQ⊥HA，交HA的延长线于点Q，
在Rt△CDQ中，CD＝160cm，
∴DQ＝CD•cs54°≈160×0.6＝96（cm），
∴96﹣80＝16（cm），
∴点C离地面的高度升高约16cm．
19．用各种盛水容器可以制作精致的家用流水景观（如图1）．
科学原理：如图2，始终盛满水的圆柱体水桶水面离地面的高度为H（单位：cm），如果在离水面竖直距离为h（单位：cm）的地方开大小合适的小孔，那么从小孔射出水的射程（水流落地点离小孔的水平距离）s（单位：cm）与h的关系式为s2＝4h（H﹣h）．
应用思考：现用高度为20cm的圆柱体塑料水瓶做相关研究，水瓶直立地面，通过连续注水保证它始终盛满水，在离水面竖直距离hcm处开一个小孔．
（1）写出s2与h的关系式；并求出当h为何值时，射程s有最大值，最大射程是多少？
（2）在侧面开两个小孔，这两个小孔离水面的竖直距离分别为a，b，要使两孔射出水的射程相同，求a，b之间的关系式；
（3）如果想通过垫高塑料水瓶，使射出水的最大射程增加16cm，求垫高的高度及小孔离水面的竖直距离．
【解答】解：（1）∵s2＝4h（H﹣h），
∴当H＝20cm时，s2＝4h（20﹣h）＝﹣4（h﹣10）2+400，
∴当h＝10cm时，s2有最大值400cm2，
∴当h＝10cm时，s有最大值20cm．
∴当h为10cm时，射程s有最大值，最大射程是20cm；
（2）∵s2＝4h（20﹣h），
设存在a，b，使两孔射出水的射程相同，则有：
4a（20﹣a）＝4b（20﹣b），
∴20a﹣a2＝20b﹣b2，
∴a2﹣b2＝20a﹣20b，
∴（a+b）（a﹣b）＝20（a﹣b），
∴（a﹣b）（a+b﹣20）＝0，
∴a﹣b＝0，或a+b﹣20＝0，
∴a＝b或a+b＝20；
（3）设垫高的高度为m，则s2＝4h（20+m﹣h）＝﹣4+（20+m）2，
∴当h＝cm时，smax＝20+m＝20+16，
∴m＝16cm，此时h＝＝18cm．
当h＝＞20时，即m＞20时，
h＝20时，S2max＝362，
362＝4×20×（20+m﹣20），
∴M＝16.2（舍弃）．
∴垫高的高度为16cm，小孔离水面的竖直距离为18cm．
20．如图，AB为⊙O的弦，OC⊥OA交AB于点P，交过点B的直线于点C，且CB＝CP．
（1）试判断直线BC与⊙O的位置关系，并说明理由；
（2）若sinA＝，OA＝8，求CB的长．
【解答】解：（1）直线BC与⊙O相切，
理由：如图，连接OB，
∵OA＝OB，
∴∠A＝∠OBA，
∵CP＝CB，
∴∠CPB＝∠CBP，
∵∠APO＝∠CPB，
∴∠APO＝∠CBP，
∵OC⊥OA，
∴∠A+∠APO＝90°，
∴∠OBA+∠CBP＝90°，
∴∠OBC＝90°，
∵OB为半径，
∴直线BC与⊙O相切；
（2）在Rt△AOP中，sinA＝，
∵sinA＝，
∴设OP＝x，则AP＝5x，
∵OP2+OA2＝AP2，
∴，
解得：x＝或﹣（不符合题意，舍去），
∴OP＝×＝4，
∵∠OBC＝90°，
∴BC2+OB2＝OC2，
∵CP＝CB，OB＝OA＝8，
∴BC2+82＝（BC+4）2，
解得：BC＝6，
∴CB的长为6．
21．【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积？
【初步尝试】如图1，已知扇形OAB，请你用圆规和无刻度的直尺过圆心O作一条直线，使扇形的面积被这条直线平分；
【问题联想】如图2，已知线段MN，请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP；
【问题再解】如图3，已知扇形OAB，请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧，使扇形的面积被这条圆弧平分．
（友情提醒：以上作图均不写作法，但需保留作图痕迹）
【解答】解：【初步尝试】如图1，直线OP即为所求；
【问题联想】如图2，三角形MNP即为所求；
【问题再解】如图3中，即为所求．
22．已知：A、B为圆上两定点，点C在该圆上，∠C为所对的圆周角．
知识回顾
（1）如图①，⊙O中，B、C位于直线AO异侧，∠AOB+∠C＝135°．
①求∠C的度数；
②若⊙O的半径为5，AC＝8，求BC的长；
逆向思考
（2）如图②，若P为圆内一点，且∠APB＜120°，PA＝PB，∠APB＝2∠C．求证：P为该圆的圆心；
拓展应用
（3）如图③，在（2）的条件下，若∠APB＝90°，点C在⊙P位于直线AP上方部分的圆弧上运动．点D在⊙P上，满足CD＝CB﹣CA的所有点D中，必有一个点的位置始终不变．请证明．
【解答】（1）解：①∵∠AOB+∠C＝135°，∠AOB＝2∠C，
∴3∠C＝135°，
∴∠C＝45°．
②连接AB，过A作AD⊥BC，垂足为M，
∵∠C＝45°，AC＝8，
∴△ACM是等腰直角三角形，且AM＝CM＝4，
∵∠AOB＝2∠C＝90°，OA＝OB，
∴△AOB是等腰直角三角形，
∴AB＝OA＝5，
在直角三角形ABM中，BM＝＝3，
∴BC＝CM+BM＝4+3＝7．
（2）延长AP交圆于点N，则∠C＝∠N，
∵∠APB＝2∠C，
∴∠APB＝2∠N，
∵∠APB＝∠N+∠PBN，
∴∠N＝∠PBN，
∴PN＝PB，
∵PA＝PB，
∴PA＝PB＝PN，
∴P为该圆的圆心．
（3）过B作BC的垂线交CA的延长线于点E，连接AB，延长AP交圆于点F，连接CF，FB，
∵∠APB＝90°，
∴∠C＝45°，
∴△BCE是等腰直角三角形，
∴BE＝BC，
∵BP⊥AF，PA＝PF，
∴BA＝BF，
∵AF是直径，
∴∠ABF＝90°，
∴∠EBC＝∠ABF＝90°，
∴∠EBA＝∠CBF，
∴△EBA≌△CBF（SAS），
∴AE＝CF，
∵CD＝CB﹣CA＝CE﹣CA＝AE，
∴CD＝CF，
∴必有一个点D的位置始终不变，点F即为所求．