2022-2023学年河北省唐山市高三上学期期末数学试题及答案

这是一份2022-2023学年河北省唐山市高三上学期期末数学试题及答案，共24页。试卷主要包含了考生必须保持答题卡的整洁， 直线与抛物线交于两点，则， 高斯， 设，则等内容，欢迎下载使用。
1.答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.将条形码横贴在答题卡上“条形码粘贴处”.
2.作答选择题时，选出每小题答案后，用2B铅笔将答题卡上对应题目选项的答案信息点涂黑;如需改动，用橡皮擦干净后，再选涂其他答案.答案不能答在试卷上.
3.非选择题必须用黑色字迹的纲笔或签字笔作答，答案必须写在答题卡各题目指定区域的相应位置内;如需改动，先划掉原来的答案，然后再写上新答案;不准使用䂏笔和涂改液.不按以上要求作答无效.
4.考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回.
一、选择题:本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知集合，则（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】解分式不等式求得集合，求函数的定义域求得集合，由此求得.
【详解】，
，解得，所以.
，所以，
所以.
故选：A
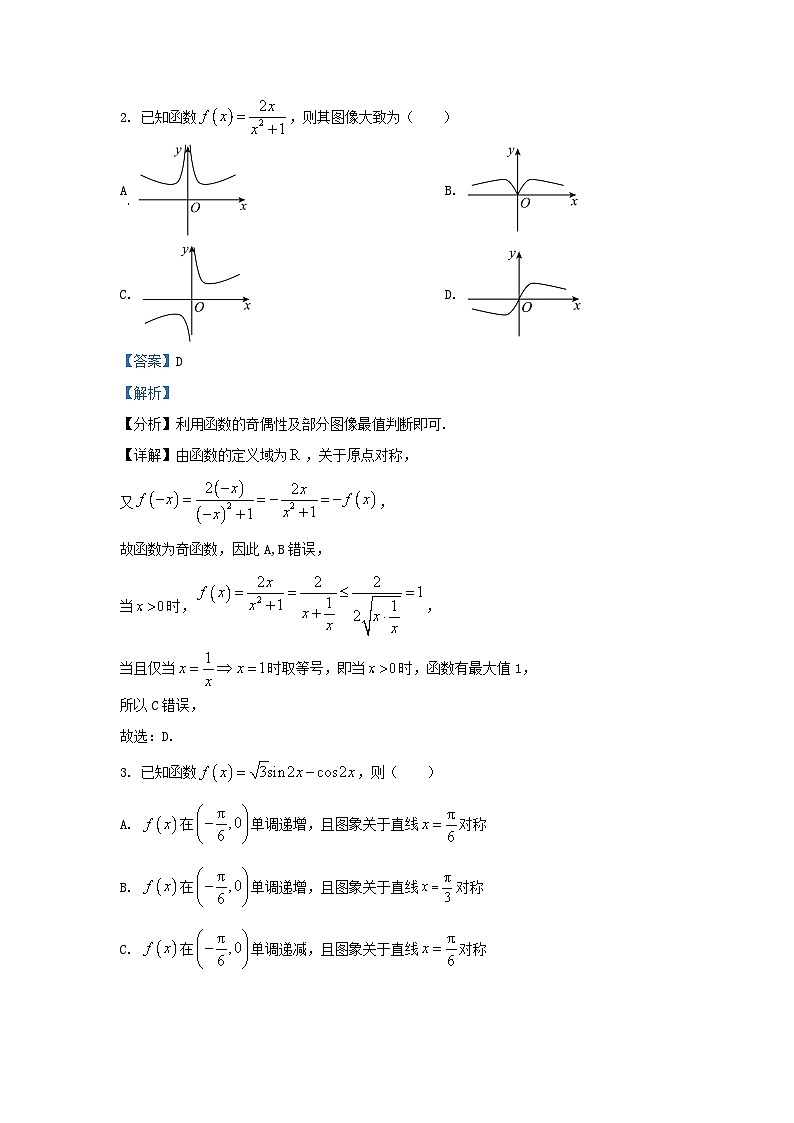
2. 已知函数，则其图像大致为（ ）
A B.
C. D.
【答案】D
【解析】
【分析】利用函数的奇偶性及部分图像最值判断即可.
【详解】由函数的定义域为，关于原点对称，
又，
故函数为奇函数，因此A,B错误，
当时，，
当且仅当时取等号，即当时，函数有最大值1，
所以C错误，
故选：D.
3. 已知函数，则（ ）
A. 在单调递增，且图象关于直线对称
B. 在单调递增，且图象关于直线对称
C. 在单调递减，且图象关于直线对称
D. 在单调递减，且图象关于直线对称
【答案】B
【解析】
【分析】化简的解析式，根据三角函数的单调性、对称性确定正确答案.
【详解】，
由于，
所以在单调递增，
，所以不关于直线对称.
，所以关于直线对称.
故选：B
4. 的展开式共有七项，且常数项为20，则（ ）
A. 1B. C. 2D.
【答案】B
【解析】
【分析】根据展开式的项数得到，进而由展开式通项公式得到，求出的值.
【详解】因为的展开式共有七项，故，
且展开式通项公式为，
令，解得：，故，解得：
故选：B
5. 直线与抛物线交于两点，则（ ）
A. 8B. C. 4D.
【答案】A
【解析】
【分析】联立直线的方程和抛物线的方程，化简写出根与系数关系，由此求得.
【详解】由，消去并化简得，，
设，则，
所以.
故选：A
6. 高斯（Gauss）被认为是历史上最重要的数学家之一，并享有“数学王子”之称.小学进行的求和运算时，他是这样算的:，共有50组，所以，这就是著名的高斯法，又称为倒序相加法.事实上，高斯发现并利用了等差数列的对称性.若函数的图象关于点对称，为数列的前项和，则下列结论中，错误的是（ ）
A.
B.
C.
D.
【答案】C
【解析】
【分析】对于A，利用函数的中心对称性公式即可求解；
对于B，利用倒序相加法求和及A选项的结论即可求解；
对于C，利用B选项的结论及与的关系，结合等差数列的前项和公式即可求解；
对于D，利用B选项的结论及裂项相消法求和即可求解.
【详解】对于A，因为函数的图象关于点对称，所以，令，
所以，故A正确；
对于B，因为
所以
因为，所以即，故B正确；
对于C，由题可知，当时，，当时，，取时，，满足此式，
故的通项公式为.所以，
而，所以.故C错误；
对于D，因为，所以，
所以，
因为，所以，即，故D正确.
故选：C.
7. 已知正三棱锥的侧棱长为2，则该三棱锥体积最大时，其外接球的表面积为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】利用正三棱锥的特点及体积公式，结合三元基本不等式及正方体的体对角线为正三棱锥的外接球的直径，然后利用球的表面积公式即可求解.
【详解】设为底面的中心，延长交于，连接,如图所示
因为三棱锥是正三棱锥，
所以平面，且是边上的中线，
设，则
，
在中，，
所以三棱锥的体积为，
因为，
可得，当且仅当，即时，等号成立，
当时，正三棱锥体积取得最大，
所以正三棱锥的侧棱长为2，底面边长为，
由此可知，该正三棱锥的侧面为等腰直角三角形，即侧棱两两垂直，则该正三棱锥的外接球为棱长为2的正方体的外接球，
所以该正三棱锥的外接球的直径为正方体的体对角线，
即，解得,
所以外接球的表面积为.
故选：C.
8. 设，则（ ）
A B.
C. D.
【答案】D
【解析】
【分析】根据已知条件构造函数，，再利用导数法研究函数的单调性，结合函数单调性的性质即可求解.
【详解】由，令，
所以，
因为，
因为，所以，，故，
所以在上单调递减，
又，所以
所以，即，所以.
由，令，
所以，所以在上单调递增，
所以，
所以，即，所以，
综上，.
故选：D.
【点睛】关键点点睛：构造，，然后利用导函数研究函数的单调性，结合函数单调性的性质即可.
二、选择题:本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.
9. 已知为虚数单位，复数，下列结论正确的有（ ）
A.
B.
C. 若，则
D. 若，则
【答案】AC
【解析】
【分析】根据复数运算、共轭复数、复数相等等知识确定正确答案.
【详解】A选项，，A选项正确.
B选项，，B选项错误
C选项，，
，
若，则，解得，所以C选项正确.
D选项，当时，，所以D选项错误.
故选：AC
10. 已知是三条不同的直线，是三个不同的平面，下列命题正确的有（ ）
A. 若，则
B. 若，则
C. 若，则
D. 若，则
【答案】BD
【解析】
【分析】根据线线、面面位置关系等知识确定正确答案.
【详解】A选项，若，则可能异面，A选项错误.
B选项，若，则，B选项正确.
C选项，若，则可能相交，C选项正确.
D选项，若，则，D选项正确.
故选：BD
11. 甲、乙、丙三人玩传球游戏，第1次由甲传出，每次传球时，传球者都等可能地将球传给另外两人中的任何一人.设第次传球后球在甲手中的概率为，则下列结论正确的有（ ）
A.
B.
C.
D.
【答案】AC
【解析】
【分析】结合全概率公式和递推数列等知识求得正确答案.
【详解】表示第次传球后球在甲手中的概率，所以，A选项正确.
表示第次传球后球在甲手中的概率，则，B选项错误.
，即，C选项正确.
，，
所以数列是首项为，公比为的等比数列，
所以，
，D选项错误.
故选：AC
12. 已知圆，动点，直线，在上的射影为点，下列结论正确的有（ ）
A. 若在圆上，则直线与圆相切
B. 若在圆内，则直线与圆相交
C. 若过点，与圆相交于点，则四边形面积的最小值为
D. 若在曲线上，则的轨迹所围成区域的面积为
【答案】ACD
【解析】
【分析】AB选项，由圆心到直线的距离与半径的关系，判断直线与圆的位置关系；C选项，求出点和点到直线的距离，求出弦长，把面积表示出来，再判断最小值；D选项，通过分类讨论，得到曲线形状，再求的轨迹，根据图形计算面积.
【详解】圆，圆心坐标为，半径，
对于A选项，若在圆上，有，
圆心到直线的距离，则直线与圆相切，A选项正确；
对于B选项，若在圆内，有，
圆心到直线的距离，则直线与圆相离，B选项错误；
对于C选项，若过点，则有，此时，，
圆心到直线的距离，点到直线的距离，，弦长，，
四边形面积，
当时，有最小值，C选项正确；
对于D选项，曲线等价于
时，有，此时；时，有，此时；
时，有，此时；时，有，此时；
曲线表示的图形为一个正方形，如图所示，
当，时，直线过定点，由，直线倾斜角，
在上的射影为点，则与直线垂直，此时点轨迹是以为直径的右半圆，如图所示，
其余类型同理可得，所以点轨迹如图所示，
所以的轨迹所围成区域的面积为，D选项正确；
故选：ACD
三、填空题:本题共4小题，每小题5分，共20分.
13. 已知是正项等比数列中的连续三项，则公比__________.
【答案】
【解析】
【分析】根据等比中项的知识求得，进而求得.
【详解】由于是正项等比数列中的连续三项，
所以且，解得（负根舍去），
所以.
故答案为：
14. 在中，分别为的中点，则__________.
【答案】－4
【解析】
【分析】由向量的线性运算得，，然后计算数量积可得．
【详解】由已知，，
．
故答案为：．
15. 圆台中,上、下底面的面积比为,其外接球的球心在线段上,若,则圆台和球的体积比为__________.
【答案】
【解析】
【分析】设上底面半径为,面积为,下底面半径为,面积为,,台体的体积为,球的半径为,球的体积为,则,,根据已知条件列出方程组,找到,,和的关系,再利用体积公式求解即可.
【详解】设上底面半径为,面积为,下底面半径为,面积为,,台体的体积为,球的半径为,球的体积为,
则,,
根据题意可得:
,
即,
解得:,
则,
所以,
,
则.
故答案为：
16. 函数，当时，，则的取值范围是__________.
【答案】
【解析】
【分析】当时，，不合题意；若，当时，可证得，，满足题意.
【详解】，当时，由，有.
，时，；时，.
，时，；时，.
则当时，不满足.
若， ，
设，，
解得，解得，在上单调递减，在上单调递增，
则，∴当时，，有，可得
所以若，当时，
若，
设，，
解得，解得，在上单调递减，在上单调递增，
，
所以若，.
综上可得：若，当时，恒成立.
则的取值范围是.
故答案为：
【点睛】方法点睛：1. 导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理．
2.利用导数解决含参函数的单调性问题时，一般将其转化为不等式恒成立问题，解题过程中要注意分类讨论和数形结合思想的应用.
3..证明不等式，构造一个适当的函数，利用它的单调性进行解题，是一种常用技巧.许多问题，如果运用这种思想去解决，往往能获得简洁明快的思路，有着非凡的功效.
四、解答题:本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17. 的内角的对边分别为，已知.
（1）若，求;
（2）求的最大值.
【答案】（1）
（2）．
【解析】
【分析】（1）由，利用正弦定理结合两角和的正弦公式得到sinAcsB＝－2csAsinB，再根据B＝，得到tanA，然后利用两角和的正切公式求解.
（2）结合tanA＝－2tanB，由tanC＝＝，利用基本不等式求解.
【小问1详解】
解：由.及正弦定理得csA＝－，
即csAsinB＝－sinC，由sinC＝sin（A＋B）＝sinAcsB＋csAsinB，
代入整理得sinAcsB＝－2csAsinB，
又B＝，则tanA＝－2tanB＝－2，
所以tanC＝－tan（A＋B）＝＝．
【小问2详解】
由知，A为钝角，B为锐角，即tanB＞0．
由（1）知tanA＝－2tanB，
所以tanC＝－tan（A＋B）＝＝＝，
≤＝．
当且仅当2tan2B＝1，即tanB＝时，等号成立．
所以tanC的最大值为．
18. 已知是等差数列，是公比不为1的等比数列，.
（1）求数列的通项公式；
（2）若集合，且，求中所有元素之和.
【答案】（1）
（2）242
【解析】
【分析】（1）结合等差、等比数列的知识求得的通项公式.
（2）根据已知条件列不等式，结合等比数列的前项和公式求得正确答案.
【小问1详解】
设等差数列公差为，等比数列的公比为，
依题意，解得，.
所以.
【小问2详解】
设，即，即，
因为，所以，即，
由于，所以，解得，，
所以中所有元素之和为.
19. 如图，在四棱锥中，底面是菱形，，，.
（1）证明：平面平面；
（2）求平面与平面夹角的余弦值.
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）取的中点，连接、，证明出平面，可得出，利用勾股定理逆定理可证得，利用线面垂直的判定定理可证得结论成立；
（2）以点为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，利用空间向量法可求得平面与平面夹角的余弦值.
【小问1详解】
证明：取的中点，连接、．
因为四边形为菱形，则，，则为等边三角形，
为的中点，则，
，，、平面，平面，
平面，，
设，则，，
又因为，，
，则，
，、平面，平面，
平面，所以，平面平面.
【小问2详解】
解：因为平面，，
以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，
则、、、，
设平面的法向量为，，，
则，取，可得，
设平面的法向量为，，，
则，取，可得，
所以，，
因此，平面与平面夹角的余弦值为.
20. 为试验一种新药，某医院把该药分发给位患有相关疾病的志愿者服用.试验方案为:若这位患者中至少有人治愈，则认为这种新药有效;否则认为这种新药无效.假设新药有效，治愈率为.
（1）用表示这位志愿者中治愈的人数，求的期望;
（2）若位志愿者中治愈的人数恰好为，从人中随机选取人，求人全部治愈的概率;
（3）求经试验认定该药无效的概率（保留4位小数）;根据值的大小解释试验方案是否合理.（依据:当值小于时，可以认为试验方案合理，否则认为不合理.）附:记，参考数据如下:
【答案】（1）
（2）
（3）答案见解析
【解析】
【分析】（1）利用二项分布的期望公式即可求解；
（2）利用组合数及古典概型的计算公式即可求解；
（3）根据已知条件及参考数据，得出随机变量的取值范围并求出相应的概率，然后进行比较即可求解.
【小问1详解】
将位患者服用新药视为重伯努利试验，在每次实验中，每位患者治愈的概率为，且每位患者是否治愈相互独立，
则，故．
【小问2详解】
设“任选位志愿者全部治愈”，则．
【小问3详解】
设 “经过试验该药被认定无效”，事件发生等价于，则
.
所以值小于，可以认为试验方案合理．
21. 已知椭圆的离心率为，点在上，不经过点的直线与交于不同的两点.
（1）求的方程;
（2）若直线与直线的斜率之和为0，求的值及的取值范围.
【答案】（1）
（2）；的取值范围为．
【解析】
【分析】（1）利用椭圆的离心率公式及点在椭圆上，结合椭圆中三者的关系即可求解；
（2）根据（1）的结论及已知条件，将直线与椭圆方程联立，消去得到关于的一元二次方程，利用直线与椭圆相交的条件及韦达定理即可求解.
【小问1详解】
由题意得，解得，
所以椭圆的标准方程为．
【小问2详解】
设，则
由得，
因为直线与椭圆相交，
所以，
所以，，
所以
，
由于，于是，
所以，所以．
由，解得．
因为直线不经过点，所以．
所以的取值范围为．
22. 已知函数.
（1）求的极值；
（2）若，证明:函数有两个零点，且.
【答案】（1）极小值为；没有极大值
（2）证明见解析
【解析】
【分析】（1）利用导数求得的极值.
（2）先求得，的大致范围，然后利用构造函数法，结合导数证得.
【小问1详解】
的定义域为，
，
在区间递减；
在区间递增.
所以的极小值是，无极大值.
【小问2详解】
由（1）知至多有两个零点，且，
构造函数，
所以在区间递减；在区间递增，
所以当时，取得最小值，所以，
所以当时，，
则，
故存在一个零点.
由于，所以，
所以，
故存在另一个零点.
由得，故，
，，要证，
只需证，即证，即证，
构造函数，
，
由于，所以，
而（当且仅当时等号成立），
所以在区间上单调递增，
所以，则，
因此.
【点睛】利用导数研究函数的极值，首先要求函数的定义域，然后利用导数求函数的单调区间，从而求得函数的极值.利用导数证明不等式，可利用构造函数法，然后结合导数求得所构造函数的单调性，从而证得不等式成立.
3
4
5
6
7
8
9
10