山西省忻州市2023年九年级上学期期末综合评估数学试题附答案

这是一份山西省忻州市2023年九年级上学期期末综合评估数学试题附答案，共15页。试卷主要包含了单选题，四象限D．仅经过第一，填空题等内容，欢迎下载使用。

1．若点是反比例函数图象上一点，则此函数图象一定经过点（ ）
A．B．C．D．
2．萌萌将如图所示的七巧板的其中几块，拼成一个多边形，所拼成的多边形中为中心对称图形的是（ ）
A．B．
C．D．
3．在如图所示的人眼成像的示意图中，可能没有蕴含的初中数学知识是（ ）
A．位似图形B．相似三角形的判定
C．旋转D．平行线的性质
4．若关于x的一元二次方程有两个不相等的实数根，则k的值可以是（ ）
A．-1B．1C．2D．3
5．如图，AB是的直径，过点A作的切线，连接，与交于点D，E是上一点，连接．若，则的度数为（ ）
A．B．C．D．
6．如图，在矩形中，M是边的中点，N为线段与的交点，则（ ）
A．B．C．D．
7．如图，四个完全相同的小球，分别写有1，2，3，4，将其放入袋子里，充分搅匀，随机将小球分成数量相同的两部分，则写有奇数的小球刚好分在一起的概率是（ ）
A．B．C．D．
8．王阿姨的水果店以4元/千克的价格购入了一批苹果，再以6元/千克的价格出售，每天可售出200千克，为了促销，王阿姨决定降价销售，销售过程中发现，这种苹果每降价0.2元/千克，每天可多售出20千克，另外，每天的房租等固定成本为50元，若王阿姨每天要想盈利250元，设应将每千克苹果的售价降低x元，则以下方程正确的为（ ）
A．
B．
C．
D．
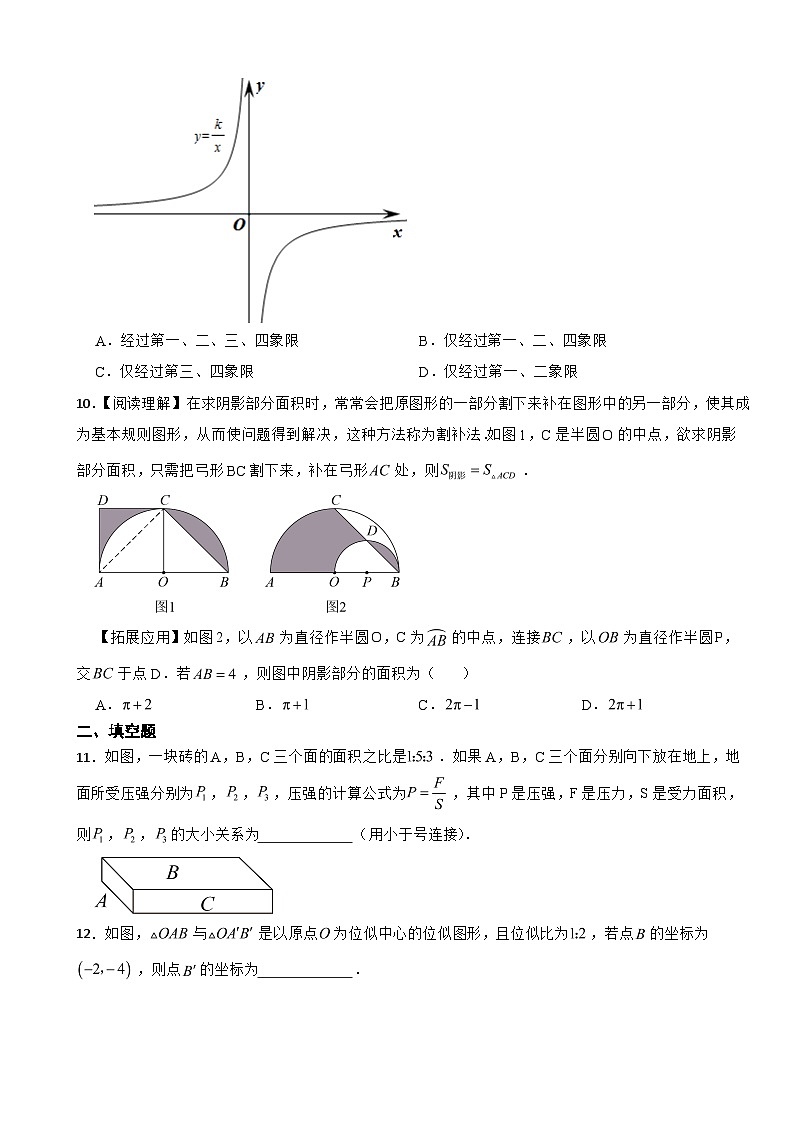
9．在平面直角坐标系中，反比例函数的图象如图所示，则二次函数的图象（ ）
A．经过第一、二、三、四象限B．仅经过第一、二、四象限
C．仅经过第三、四象限D．仅经过第一、二象限
10．【阅读理解】在求阴影部分面积时，常常会把原图形的一部分割下来补在图形中的另一部分，使其成为基本规则图形，从而使问题得到解决，这种方法称为割补法．如图1，C是半圆O的中点，欲求阴影部分面积，只需把弓形BC割下来，补在弓形处，则．
【拓展应用】如图2，以为直径作半圆O，C为的中点，连接，以为直径作半圆P，交于点D．若，则图中阴影部分的面积为（ ）
A．B．C．D．
二、填空题
11．如图，一块砖的A，B，C三个面的面积之比是．如果A，B，C三个面分别向下放在地上，地面所受压强分别为，，，压强的计算公式为，其中P是压强，F是压力，S是受力面积，则，，的大小关系为 （用小于号连接）．
12．如图，与是以原点为位似中心的位似图形，且位似比为，若点的坐标为，则点的坐标为 ．
13．数学中，把这个比例称为黄金分割比例．鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例，是自然界最美的鬼斧神工．如图，P是AB的黄金分割点（），若线段的长为，则BP的长为 ．
14．已知二次函数，当时，函数y的最小值为，则m的值为 ．
15．如图，直线与坐标轴分别相交于A，B两点，过A，B两点作矩形，，双曲线上在第一象限经过C，D两点，则k的值是 ．
三、解答题
16．
（1）如图，绕点逆时针旋转某个角度得到（点的对应点为点，点的对应点为点）．已知，，求的度数．
（2）下面是某同学解方程的部分运算过程：
①该同学的解答从第 ▲ 步开始出错；
②请写出正确的解答过程．
17．如图，已知线段AB，及．
（1）求作线段CE，使得点C在射线BM上，且，点E在线段AB上，且；（要求：尺规作图，不写作法，保留作图痕迹）
（2）在（1）的条件下，求证：．
18．为庆祝党的二十大胜利召开，某学校举行作文比赛，题目有“伟大的中国共产党”“科技托起强国梦”“家乡的新变化”“时代赋予我们的使命”（分别用字母A，B，C，D依次表示这四个题目）．比赛时，将A，B，C，D这四个字母分别写在4张无差别不透明的卡片的正面上，洗匀后正面向下放在桌面上，小青先从中随机抽取一张卡片，放回后洗匀，再由小云从中随机抽取一张卡片，进行比赛．
（1）小云抽中题目“时代赋予我们的使命”的概率是 ．
（2）试用画树状图或列表的方法表示所有可能的结果，并求出小青和小云抽中不同题目的概率．
19．如图，在平面直角坐标系中，，轴，，双曲线经过点B，将绕点B逆时针旋转，使点O的对应点D在x轴的正半轴上．若的对应线段恰好经过点O．
（1）求双曲线的解析式．
（2）小彬通过观察图形得出一个结论：点C在双曲线上．请你证明这个结论的正确性．
20．阅读与思考
九年级学生小刚喜欢看书，他在学习了圆后，在家里突然看到某本数学书上居然还有一个相交弦定理（圆内的两条相交弦，被交点分成的两条线段长的积相等），下面是书上的证明过程，请仔细阅读，并完成相应的任务．
任务：
（1）请将上述证明过程补充完整．
根据： ；@： ．
（2）小刚又看到一道课后习题，如图2，AB是的弦，P是上一点，，，，求的半径．
21．如图，一次函数的图象与反比例函数的图象交于A，B两点，与x轴交于点C，与y轴交于点D，已知点A的坐标为，点B的坐标为．
（1）求反比例函数与一次函数的解析式．
（2）结合图象，请直接写出不等式的解集．
（3）在y轴上是否存在一点P，使得与相似，且点P不与原点O重合？若存在，求出点P的坐标；若不存在，说明理由．
22．综合与实践
在矩形中，，，三角板的直角顶点E在矩形的边上，，将绕点E旋转．
（1）如图1，当直角边EF经过点B，的延长线经过点C时．
①求证：．
②求的长．
（2）如图2，旋转，若点F落在的延长线上，与交于点H，且H为的中点，的延长线与的延长线交于点M，连接，求的度数．
23．综合与探究
如图，抛物线经过，两点，与轴交于点，作直线．
（1）求抛物线和直线的函数解析式．
（2）是直线上方抛物线上一点，求面积的最大值及此时点的坐标．
（3）在抛物线对称轴上是否存在一点，使得以点，，为顶点的三角形是等腰三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．
1．D
2．B
3．C
4．A
5．A
6．D
7．C
8．B
9．A
10．B
11．
12．（4，8）
13．
14．
15．
16．（1）解：由旋转的性质可得：
∴
∵，，
∴；
（2）解：①四；
②
移项，得，
配方，得，即，
两边开平方，得或
解得：．
17．（1）解：如图所示：
（2）证明：∵，，
∴，
∵，
∴，
∴，
∴，
∵为公共角，
∴，
∴，
∴．
18．（1）
（2）解：列表如下：
一共有16种结果，每种结果出现的可能性相同，其中小青和小云抽中不同题目的结果有12种，
所以小青和小云抽中不同题目的概率为．
19．（1）解：∵轴，
∴，
∵，
∴，
∵，
∴，
∴是等边三角形，
∴，，
过点B作轴，
∴，
∴，
∴；
∵双曲线经过点B，
∴．
∴双曲线的解析式为．
（2）证明：∵，
∴，
∴，
∵，
∴，
∴，
∴，
∵，
∴点C在双曲线上．
20．（1）有两个角对应相等的两个三角形相似；
（2）解：延长交圆O于点D，延长交圆O于点F，
设圆O的半径为r，则，，
根据（1）中结论得，即为，
解得：或（不符合题意，舍去），
的半径为．
21．（1）解：把A代入反比例解析式得：，即，
则反比例解析式为；
∵点B的坐标为，
∴，
解得：，
∴，
把A与B坐标代入一次函数解析式得：，
解得：，
∴一次函数的解析式为；
（2）解：或；
（3）解：P与O不重合，在y轴上存在一点P，使得与相似，理由为：过点C作，交y轴于点P，如图所示，
∵C、D两点在直线上，
当时，，当时，，
∴C、D的坐标分别为，，
∴，，，
∵，
∴=，即，
解得：，
∴，
则点P的坐标为．
综上所示，P的坐标为．
22．（1）解：①∵四边形为矩形，三角板为直角三角形，
∴，
∴，
∴，
∵，
∴；
②∵四边形为矩形，
∴，
由①得，
∴，即，
解得：；
（2）解：∵四边形为矩形，三角板为直角三角形，
∴，
∴
∴，
∵，
∴，
由②得，
∵H为的中点，
∴，
∴，
∴，
在与中，
，
∴，
∴，
∴，
∴，
∵，
∴，
∵，
∴．
23．（1）解：把，代入得，
，解得，
，
，
，
设直线的解析式为，
把 代入得，
，
，
；
（2）解：如图，
过点 作 于点 交 于点，
设， ，
，
，
，
当时，的最大值为，
，
；
（3）解：存在，点的坐标为或 或或 或．解：移项，得，…………………第一步
配方，得，………………第二步
即，………………………………第三步
两边开平方，得，……………………第四步
…
圆的两条弦相交，这两条弦被交点分成的两条线段的积相等．
已知：如图1，的两弦相交于点P．
求证：．
证明：
如图1，连接．
∵，．
∴，（根据）
∴@，
∴，
∴两条弦相交，被交点分成的两条线段的积相等．
A
B
C
D
A
（A，A）
（A，B）
（A，C）
（A，D）
B
（B，A）
（B，B）
（B，C）
（B，D）
C
（C，A）
（C，B）
（C，C）
（C，D）
D
（D，A）
（D，B）
（D，C）
（D，D）