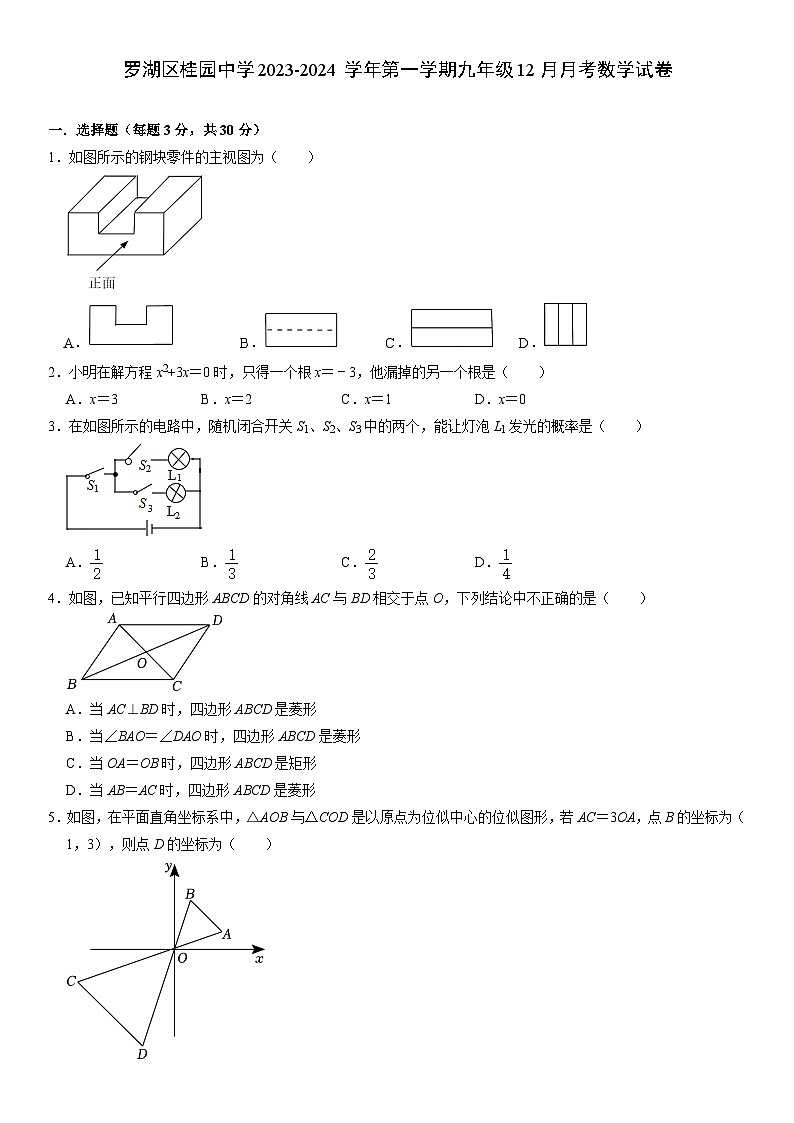
广东省深圳市罗湖区桂园中学2023-2024学年上学期九年级12月月考数学试卷

这是一份广东省深圳市罗湖区桂园中学2023-2024学年上学期九年级12月月考数学试卷，共22页。试卷主要包含了如图所示的钢块零件的主视图为等内容，欢迎下载使用。
一．选择题（每题3分，共30分）
1．如图所示的钢块零件的主视图为（ ）
A． B． C． D．
2．小明在解方程x2+3x＝0时，只得一个根x＝﹣3，他漏掉的另一个根是（ ）
A．x＝3B．x＝2C．x＝1D．x＝0
3．在如图所示的电路中，随机闭合开关S1、S2、S3中的两个，能让灯泡L1发光的概率是（ ）
A．B．C．D．
4．如图，已知平行四边形ABCD的对角线AC与BD相交于点O，下列结论中不正确的是（ ）
A．当AC⊥BD时，四边形ABCD是菱形
B．当∠BAO＝∠DAO时，四边形ABCD是菱形
C．当OA＝OB时，四边形ABCD是矩形
D．当AB＝AC时，四边形ABCD是菱形
5．如图，在平面直角坐标系中，△AOB与△COD是以原点为位似中心的位似图形，若AC＝3OA，点B的坐标为（1，3），则点D的坐标为（ ）
A．（2，6）B．（﹣2，﹣6）C．（3，9）D．（﹣3，﹣9）
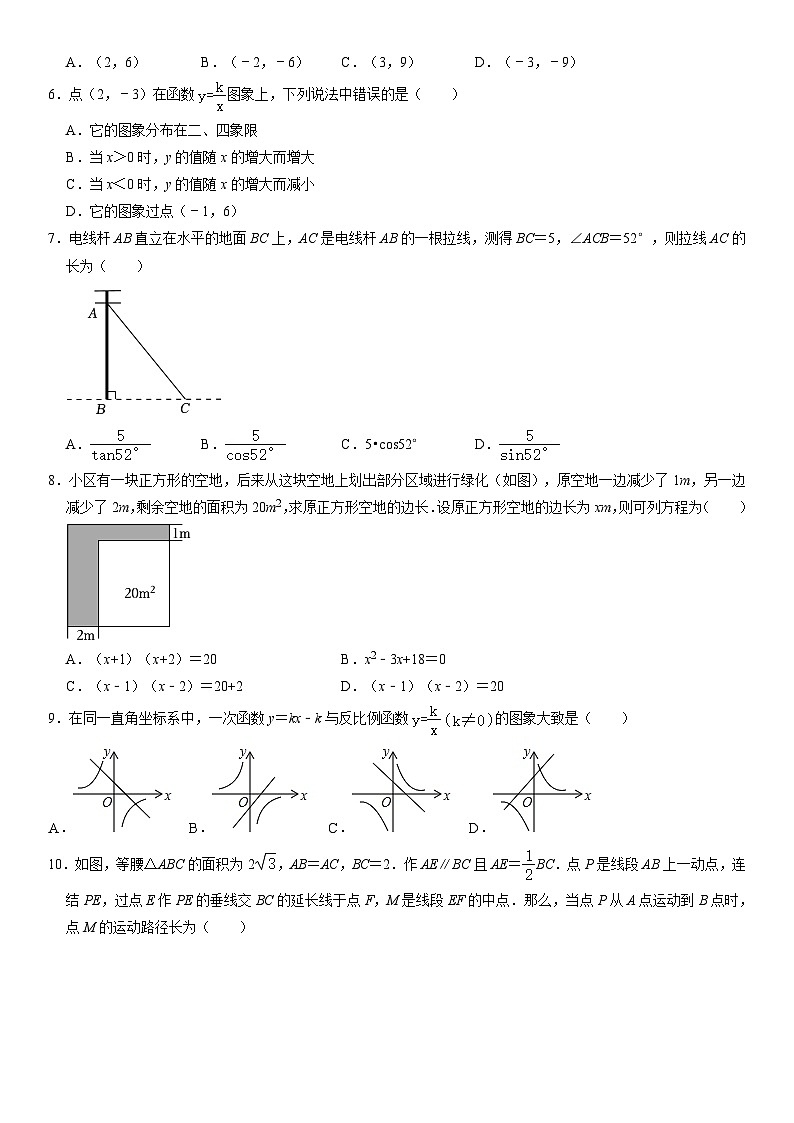
6．点（2，﹣3）在函数图象上，下列说法中错误的是（ ）
A．它的图象分布在二、四象限
B．当x＞0时，y的值随x的增大而增大
C．当x＜0时，y的值随x的增大而减小
D．它的图象过点（﹣1，6）
7．电线杆AB直立在水平的地面BC上，AC是电线杆AB的一根拉线，测得BC＝5，∠ACB＝52°，则拉线AC的长为（ ）
A．B．C．5•cs52°D．
8．小区有一块正方形的空地，后来从这块空地上划出部分区域进行绿化（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为20m2，求原正方形空地的边长．设原正方形空地的边长为xm，则可列方程为（ ）
A．（x+1）（x+2）＝20B．x2﹣3x+18＝0
C．（x﹣1）（x﹣2）＝20+2D．（x﹣1）（x﹣2）＝20
9．在同一直角坐标系中，一次函数y＝kx﹣k与反比例函数的图象大致是（ ）
A．B．C．D．
10．如图，等腰△ABC的面积为2，AB＝AC，BC＝2．作AE∥BC且AE＝BC．点P是线段AB上一动点，连结PE，过点E作PE的垂线交BC的延长线于点F，M是线段EF的中点．那么，当点P从A点运动到B点时，点M的运动路径长为（ ）
A．B．3C．2D．4
二．填空题（每题3分，共15分）
11．如图，AB∥CD∥EF，若，BD＝3，则DF＝ ．
12．已知关于x的一元二次方程x2﹣5x＋2＝0，它的根是 ．
13．一个盒中有8枚黑棋子和若干枚白棋子，这些棋子除颜色外无其他差别．从盒中随机取出一枚棋子，记下颜色，再放回盒中．不断重复上述过程，一共取了300次，其中有100次取到黑棋子，由此估计盒中有 枚白棋子．
14．如图，点P在反比例函数的图象上，PA⊥x轴于点A，PB⊥y轴于点B，PA＝PB．一次函数y＝x+1的图象与PB交于点D，若D为PB的中点，则k的值为 ．
15．如图，在矩形ABCD中，将∠ABC绕点A按逆时针方向旋转一定角度后，BC的对应边B'C'交CD边于点G．连接BB'、CC'．若AD＝7，CG＝4，AB'＝B'G，则＝ （结果保留根号）．
三．解答题（共55分）
16．（5分）计算：（）﹣1+4cs45°﹣+（2023﹣π）0．
17．（8分）在4月23日“世界读书日”来临之际，某校为了了解学生的课外阅读情况，从全校随机抽取了部分学生，调查了他们平均每周的课外阅读时间t（单位：小时）﹒把调查结果分为四档，A档：t＜8；B档：8≤t＜9；C档：9≤t＜10；D档：t≥10．根据调查情况，绘制了如图所示的两幅不完整统计图，根据图中信息解答问题：
（1）本次调查的学生共有 人；扇形统计图中，C档对应的圆心角度数为 ；请将条形统计图补充完整；
（2）学校要从D档的4名学生中随机抽取2名作读书经验分享，已知这4名学生中1名来自七年级，1名来自八年级，2名来自九年级，请用列表或画树状图的方法，求抽到的2名学生来自不同年级的概率．
18．（6分）消防车是救援火灾的重要装备．图1是一辆登高云梯消防车的实物图，图2是其工作示意图，起重臂AB可伸缩，伸缩范围为10m≤AB≤40m，且起重臂AB可绕点A在一定范围内转动，张角为∠CAB，张角范围为90°≤∠CAB≤150°，转动点A距离地面MN的高度AC为5m．（参考数据：
（1）当起重臂AB长度为20m，张角为135°时，云梯消防车最高点B距地面的高度为________m；（结果保留根号）
（2）某栋楼高39m，若该楼中有居民家突发险情，请问该消防车能否实施有效救援？请说明理由．
19．（8分）如图，在菱形ABCD中，P是它对角线上面的一个点，连接CP后并延长，交CD于点E，交BA的延长线于点F．
（1）求证：∠DCP＝∠DAP；
（2）如果PE＝4，EF＝7，求线段PC的长．
20．（8分）2022年冬奥会在北京顺利召开，冬奥会吉祥物冰墩墩公仔爆红．据统计冰墩墩公仔在某电商平台1月份的销售量是5万件，3月份的销售量是7.2万件．
（1）若该平台1月份到3月份的月平均增长率都相同，求月平均增长率是多少？
（2）市场调查发现，某一间店铺冰墩墩公仔的进价为每件60元，若售价为每件100元，每天能销售20件，售价每降价1元，每天可多售出2件，为了推广宣传，商家决定降价促销，同时尽量减少库存，若使销售该公仔每天获利1200元，则售价应降低多少元？
21．（10分）我们定义：如果一个矩形A周长和面积都是B矩形的N倍，那么我们就称矩形A是矩形B的完全N倍体．
（1）若矩形A为正方形，是否存在一个正方形B是正方形A的完全2倍体？ （填“存在”或“不存在”）．
【深入探究】长为3，宽为2的矩形C是否存在完全2倍体？
小鸣和小棋分别有以下思路：
【小鸣方程流】设新矩形长和宽为x、y，则依题意x+y＝10，xy＝12，联立，得x2﹣10x+12＝0，再探究根的情况；
【小棋函数流】如图，也可用反比例函数l2：与一次函数l1：y＝﹣x+10来研究，作出图象，有交点，意味着存在完全2倍体．
（2）那么长为4．宽为3的矩形C是否存在完全倍体？请利用上述其中一种思路说明原因；
（3）如果长为5，宽为4的矩形C存在完全k倍体，请直接写出k需要满足的不等式．
22．（10分）某“数学学习兴趣小组”成员在复习《图形的变化》时，对下面的图形背景产生了浓厚的兴趣，并尝试运用由“特殊到一般”的思想进行了探究：
【问题背景】如图1，正方形ABCD中，点E为AB边上一点，连接DE，过点E作EF⊥DE交BC边于点F，将△ADE沿直线DE折叠后，点A落在点A'处，当∠BEF＝25°，则∠FEA'＝ °．
【特例探究】如图2，连接DF，当点A'恰好落在DF上时，求证：AE＝2A'F．
【深入探究】如图3，若把正方形ABCD改成矩形ABCD，且AD＝mAB，其他条件不变，他们发现AE与A′F之间也存在着一定的数量关系，请直接写出AE与A′F之间的数量关系式．
【拓展探究】如图4，若把正方形ABCD改成菱形ABCD，且∠B＝60°，∠DEF＝120°，其他条件不变，当AE＝2时，请直接写出A′F的长．
参考答案与试题解析
一．选择题（共10小题）
1．如图所示的钢块零件的主视图为（ ）
A．B．
C．D．
【解答】解：从正面看是一个“凹”字形，
故选：A．
2．小明在解方程x2+3x＝0时，只得一个根x＝﹣3，他漏掉的另一个根是（ ）
A．x＝3B．x＝2C．x＝1D．x＝0
【解答】解：x2+3x＝0，
x（x+3）＝0，
x1＝0，x2＝﹣3．
故选：D．
3．在如图所示的电路中，随机闭合开关S1、S2、S3中的两个，能让灯泡L1发光的概率是（ ）
A．B．C．D．
【解答】解：画树状图得：
∵共有6种等可能的结果，能让灯泡L1发光的有2种情况，
∴能让灯泡L1发光的概率为＝．
故选：B．
4．如图，已知平行四边形ABCD的对角线AC与BD相交于点O，下列结论中不正确的是（ ）
A．当AC⊥BD时，四边形ABCD是菱形
B．当∠BAO＝∠DAO时，四边形ABCD是菱形
C．当OA＝OB时，四边形ABCD是矩形
D．当AB＝AC时，四边形ABCD是菱形
【解答】解：A．∵AB⊥AD，
∴∠BAD＝90°，
∴平行四边形ABCD是矩形，
故结论正确，但不符合题意；
B．∵AC⊥BD，
∴平行四边形ABCD是菱形，
故结论正确，但不符合题意；
C．∵四边形ABCD是平行四边形，
∴AO＝AC，BO＝BD，
又∵OA＝OB，
∴AC＝BD，
∴平行四边形ABCD是矩形，
故结论正确，但不符合题意；
D．当AB＝AC时，四边形ABCD不一定是菱形，
故结论错误，符合题意．
故选：D．
5．如图，在平面直角坐标系中，△AOB与△COD是以原点为位似中心的位似图形，若AC＝3OA，点B的坐标为（1，3），则点D的坐标为（ ）
A．（2，6）B．（﹣2，﹣6）C．（3，9）D．（﹣3，﹣9）
【解答】解：∵AC＝3OA，
∴＝，
∵△AOB与△COD是以原点为位似中心的位似图形，
∴△AOB∽△COD，且相似比为1：2，
∵B的坐标为（1，3），
∴点D的坐标为（1×（﹣2），3×（﹣2）），即（﹣2，﹣6），
故选：B．
6．点（2，﹣3）在函数图象上，下列说法中错误的是（ ）
A．它的图象分布在二、四象限
B．当x＞0时，y的值随x的增大而增大
C．当x＜0时，y的值随x的增大而减小
D．它的图象过点（﹣1，6）
【解答】解：∵点（2，﹣3）在函数图象上，
∴k＝2×（﹣3）＝﹣6＜0，
∴反比例函数的解析式为y＝﹣，
∴它的图象分布在二、四象限，当x＞0时，y的值随x的增大而增大，当x＜0时，y的值随x的增大而增大，它的图象过点（﹣1，6）
故选项A、B、D不符合题意，C选项符合题意．
故选：C．
7．电线杆AB直立在水平的地面BC上，AC是电线杆AB的一根拉线，测得BC＝5，∠ACB＝52°，则拉线AC的长为（ ）
A．B．C．5•cs52°D．
【解答】解：∵∠ABC＝90°，∠ACB＝52°，BC＝5，
∴cs52°＝＝，
∴AC＝
故选：B．
8．小区有一块正方形的空地，后来从这块空地上划出部分区域进行绿化（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为20m2，求原正方形空地的边长．设原正方形空地的边长为xm，则可列方程为（ ）
A．（x+1）（x+2）＝20B．x2﹣3x+18＝0
C．（x﹣1）（x﹣2）＝20+2D．（x﹣1）（x﹣2）＝20
【解答】解：设原正方形的边长为x m，依题意有
（x﹣1）（x﹣2）＝20，
故选：D．
9．在同一直角坐标系中，一次函数y＝kx﹣k与反比例函数的图象大致是（ ）
A．B．
C．D．
【解答】解：当k＞0时，﹣k＜0，
∴反比例函数的图象在一、三象限，一次函数y＝kx﹣k的图象经过一、三、四象限，故C，D错误；
当k＜0时，﹣k＞0，
∴反比例函数的图象在二、四象限，一次函数y＝kx﹣k的图象经过一、二、四象限，故B选项错误，A选项正确；
故选：A．
10．如图，等腰△ABC的面积为2，AB＝AC，BC＝2．作AE∥BC且AE＝BC．点P是线段AB上一动点，连结PE，过点E作PE的垂线交BC的延长线于点F，M是线段EF的中点．那么，当点P从A点运动到B点时，点M的运动路径长为（ ）
A．B．3C．2D．4
【解答】解：如图，过点A作AH⊥BC于点H．
当点P与A重合时，点F与C重合，当点P与B重合时，点F的对应点为F″，
点M的运动轨迹是△ECF″的中位线，M′M″＝CF″，
∵AB＝AC，AH⊥BC，
∴BH＝CH，
∵AE∥BC，AE＝BC，
∴AE＝CH，
∴四边形AHCE是平行四边形，
∵∠AHC＝90°，
∴四边形AHCE是矩形，
∴EC⊥BF″，AH＝EC，
∵BC＝2，S△ABC＝2，
∴×2×AH＝2，
∴AH＝EC＝2，
∵∠BEF″＝∠ECB＝∠ECF″，
∴∠BEC+∠CEF″＝90°，
∠CEF″+∠F″＝90°，
∴∠BEC＝∠F″，
∴△ECB∽△F″CE，
∴EC2＝CB•CF″，
∴CF″＝＝6，
∴M′M″＝3
故选：B．
二．填空题（共5小题）
11．如图，AB∥CD∥EF，若，BD＝3，则DF＝ 3 ．
【解答】解：∵AB∥CD∥EF，
∴，
∵BD＝3，
∴BF＝6，
∴DF＝BF﹣BD＝6﹣3＝3．
故答案为：3．
12．已知关于x的一元二次方程x2﹣5x＋2＝0，它的根是 ．
【解答】解：解方程，得x＝．
故答案为：．
13．一个盒中有8枚黑棋子和若干枚白棋子，这些棋子除颜色外无其他差别．从盒中随机取出一枚棋子，记下颜色，再放回盒中．不断重复上述过程，一共取了300次，其中有100次取到黑棋子，由此估计盒中有 16 枚白棋子．
【解答】解：∵共取了300次，其中有100次取到黑棋子，
∴摸到黑色棋子的概率约为＝，
∴摸到白色棋子的概率约为1﹣＝，
∵共有10可黑色棋子，
∴设有x个白色棋子，则，
解得：x＝16，
故答案为：16．
14．如图，点P在反比例函数的图象上，PA⊥x轴于点A，PB⊥y轴于点B，PA＝PB．一次函数y＝x+1的图象与PB交于点D，若D为PB的中点，则k的值为 4 ．
【解答】解：设一次函数图象与x轴的交点为M，与y轴的交点为N，则M（﹣1，0），N（0，1），
∴OM＝ON＝1，
∵PA⊥x轴于点A，PB⊥y轴于点B，PA＝PB，
∴四边形AOBP是正方形，
∴PB∥x轴，PB＝OB，
∴△DBN∽△MON，
∴＝＝1，
∴BD＝BN，
∵D为PB的中点，
∴N为OB的中点，
∴OB＝2ON＝2，
∴PB＝OB＝2，
∴P（2，2），
∵点P在反比例函数的图象上，
∴k＝2×2＝4，
故答案为：4．
15．如图，在矩形ABCD中，将∠ABC绕点A按逆时针方向旋转一定角度后，BC的对应边B'C'交CD边于点G．连接BB'、CC'．若AD＝7，CG＝4，AB'＝B'G，则＝ （结果保留根号）．
【解答】解：连接AC，AG，AC'，
由旋转可得，AB＝AB'，AC＝AC'，∠BAB'＝∠CAC'，
∴＝，
∴△ABB'∽△ACC'，
∴＝，
∵AB'＝B'G，∠AB'G＝∠ABC＝90°，
∴△AB'G是等腰直角三角形，
∴AG＝AB'，
设AB＝AB'＝x，则AG＝x，DG＝x﹣4，
∵Rt△ADG中，AD2+DG2＝AG2，
∴72+（x﹣4）2＝（x）2，
解得x1＝5，x2＝﹣13（舍去），
∴AB＝5，
∴Rt△ABC中，AC＝＝＝，
∴＝＝，
故答案为：．
三．解答题（共7小题）
16．计算：（）﹣1+4cs45°﹣+（2023﹣π）0．
【解答】解：原式＝2+4×﹣2+1
＝2+2﹣2+1
＝3．
17．在4月23日“世界读书日”来临之际，某校为了了解学生的课外阅读情况，从全校随机抽取了部分学生，调查了他们平均每周的课外阅读时间t（单位：小时）﹒把调查结果分为四档，A档：t＜8；B档：8≤t＜9；C档：9≤t＜10；D档：t≥10．根据调查情况，绘制了如图所示的两幅不完整统计图，根据图中信息解答问题：
（1）本次调查的学生共有 40 人；扇形统计图中，C档对应的圆心角度数为 108° ；请将条形统计图补充完整；
（2）学校要从D档的4名学生中随机抽取2名作读书经验分享，已知这4名学生中1名来自七年级，1名来自八年级，2名来自九年级，请用列表或画树状图的方法，求抽到的2名学生来自不同年级的概率．
【解答】解：（1）本次调查的学生共有16÷40%＝40（人），
扇形统计图中，C档对应的圆心角度数为360°×＝108°，
A档人数为40﹣（16+12+4）＝8（人），
补全图形见解答：
故答案为：40、108°；
（2）用A表示七年级学生，用B表示八年级学生，用C和D分别表示九年级学生，画树状图如下，
因为共有12种等可能的情况数，其中抽到的2名学生来自不同年级的有10种，
所以抽到的2名学生来自不同年级的概率是＝．
18．消防车是救援火灾的重要装备．图1是一辆登高云梯消防车的实物图，图2是其工作示意图，起重臂AB可伸缩，伸缩范围为10m≤AB≤40m，且起重臂AB可绕点A在一定范围内转动，张角为∠CAB，张角范围为90°≤∠CAB≤150°，转动点A距离地面MN的高度AC为5m．（参考数据：
（1）当起重臂AB长度为20m，张角为135°时，云梯消防车最高点B距地面的高度为________m；（结果保留根号）
（2）某栋楼高39m，若该楼中有居民家突发险情，请问该消防车能否实施有效救援？请说明理由．
【解答】解：（1）过点B作BD⊥AD，交CA的延长线于点D，过点B作BE⊥MN，垂足为E．
∵BD⊥AD，BE⊥MN，DC⊥MN，
∴四边形DBEC是矩形．
∴BE＝DC．
由题意，知∠CAB＝135°，
∴∠DAB＝45°．
在Rt△ADB中，
∵cs∠DAB＝，
∴AD＝AB•cs∠DAB
＝20×cs45°
＝20×
＝10．
∴CD＝AC+AD
＝5+10．
∴BE＝5+10．
答：当起重臂AB长度为20m，张角为135°时，云梯消防车最高点B距地面的高度为（5+10）m；
（2）该消防车能实施有效救援．
理由：当BE＝39m时，
∵AC＝5m，
∴AD＝34m．
在Rt△ADB中，当AB＝40m时，
∵cs∠DAB＝＝＝0.85，
∴∠DAB≈31.788°．
∴∠CAB＝148.212°．
∵张角∠CAB范围为90°≤∠CAB≤150°，
∴该消防车能实施有效救援．
19．如图，在菱形ABCD中，P是它对角线上面的一个点，连接CP后并延长，交CD于点E，交BA的延长线于点F．
（1）求证：∠DCP＝∠DAP；
（2）如果PE＝4，EF＝7，求线段PC的长．
【解答】（1）证明：∵四边形ABCD是菱形，
∴AD＝CD，BD平分∠ADC，
∴∠ADP＝∠CDP，
在△ADP与△CDP中，
，
∴△ADP＝△CDP（SAS），
∴∠DAP＝∠DCP；
（2）解：由（1）得：△ADP＝△CDP，
∴∠DAP＝∠DCP，
∵CD∥AB，
∴∠DCF＝∠DAP＝∠CFB，
又∵∠FPA＝∠FPA，
∴△APE∽△FPA，
∴，
∴PA2＝PE•PF，
∵△ADP≌△CDP，
∴PA＝PC，
∴PC2＝PE•PF，
∵PE＝4，EF＝7，
∴PF＝11，
∴．
20．2022年冬奥会在北京顺利召开，冬奥会吉祥物冰墩墩公仔爆红．据统计冰墩墩公仔在某电商平台1月份的销售量是5万件，3月份的销售量是7.2万件．
（1）若该平台1月份到3月份的月平均增长率都相同，求月平均增长率是多少？
（2）市场调查发现，某一间店铺冰墩墩公仔的进价为每件60元，若售价为每件100元，每天能销售20件，售价每降价1元，每天可多售出2件，为了推广宣传，商家决定降价促销，同时尽量减少库存，若使销售该公仔每天获利1200元，则售价应降低多少元？
【解答】解：（1）设月平均增长率是x，
依题意得：5（1+x）2＝7.2，
解得：x1＝0.2＝20%，x2＝﹣2.2（不合题意，舍去）．
答：月平均增长率是20%．
（2）设售价应降低y元，则每件的销售利润为（100﹣y﹣60）元，每天的销售量为（20+2y）件，
依题意得：（100﹣y﹣60）（20+2y）＝1200，
整理得：y2﹣30y+200＝0，
解得：y1＝10，y2＝20．
又∵要尽量减少库存，
∴y＝20．
答：售价应降低20元．
21．我们定义：如果一个矩形A周长和面积都是B矩形的N倍，那么我们就称矩形A是矩形B的完全N倍体．
（1）若矩形A为正方形，是否存在一个正方形B是正方形A的完全2倍体？ 不存在 （填“存在”或“不存在”）．
【深入探究】长为3，宽为2的矩形C是否存在完全2倍体？
小鸣和小棋分别有以下思路：
【小鸣方程流】设新矩形长和宽为x、y，则依题意x+y＝10，xy＝12，联立，得x2﹣10x+12＝0，再探究根的情况；
【小棋函数流】如图，也可用反比例函数l2：与一次函数l1：y＝﹣x+10来研究，作出图象，有交点，意味着存在完全2倍体．
（2）那么长为4．宽为3的矩形C是否存在完全倍体？请利用上述其中一种思路说明原因；
（3）如果长为5，宽为4的矩形C存在完全k倍体，请直接写出k需要满足的不等式．
【解答】解：（1）假设存在一个正方形B是正方形A的完全2倍体，则正方形B的周长是正方形A周长的2倍，
∴正方形B的边长是正方形A边长的2倍，
∴正方形B的面积是正方形A面积的4倍，这与“完全2倍体”矛盾，所以不存在一个正方形B是正方形A的完全2倍体．
故答案为：不存在．
（2）方法1：设新矩形长和宽为x、y，则依题意得x+y＝，xy＝6，联立，得2x2﹣7x+12＝0，
∴Δ＝（﹣7）2﹣4×2×12＝﹣47＜0，
∴方程无解，
∴长为4，宽为3的矩形C不存在完全倍体．
方法2：如图，反比例函数：y＝与一次函数：y＝﹣x+没有交点，所以不存在完全倍体．
（3）设新矩形长和宽为x、y，则依题意得x+y＝9k，xy＝20k，
∴x2﹣9kx+20k＝0，
∴Δ＝（﹣9k）2﹣4×1×20k＝81k2﹣80k≥0，
∴k≥．
22．某“数学学习兴趣小组”成员在复习《图形的变化》时，对下面的图形背景产生了浓厚的兴趣，并尝试运用由“特殊到一般”的思想进行了探究：
【问题背景】如图1，正方形ABCD中，点E为AB边上一点，连接DE，过点E作EF⊥DE交BC边于点F，将△ADE沿直线DE折叠后，点A落在点A'处，当∠BEF＝25°，则∠FEA'＝ 25 °．
【特例探究】如图2，连接DF，当点A'恰好落在DF上时，求证：AE＝2A'F．
【深入探究】如图3，若把正方形ABCD改成矩形ABCD，且AD＝mAB，其他条件不变，他们发现AE与A′F之间也存在着一定的数量关系，请直接写出AE与A′F之间的数量关系式．
【拓展探究】如图4，若把正方形ABCD改成菱形ABCD，且∠B＝60°，∠DEF＝120°，其他条件不变，当AE＝2时，请直接写出A′F的长．
【解答】【问题背景】：解：∵EF⊥DE，∠BEF＝25°，
∴∠AED＝65°，
∵将△ADE沿直线DE折叠后，点A落在点A'处，
∴∠AED＝∠A'ED＝65°，
∴∠FEA'＝25°，
故答案为：25；
【特例探究】：证明：∵将△ADE沿直线DE折叠后，当点A'恰好落在DF上时，
∴AE＝A'E，∠A＝∠DA'E＝90°，
∴∠B＝∠EA'F＝90°，
∵∠AED+∠BEF＝90°＝∠DEA'+∠FEA'，
∴∠BEF＝∠FEA'，
又∵EF＝EF，
∴△BEF≌△A'EF（AAS），
∴BE＝A'E＝AE，A'F＝BF，
∴AE＝AD，
∵∠AED+∠BEF＝90°＝∠AED+∠ADE，
∴∠BEF＝∠ADE，
∴tan∠ADE＝tan∠BEF＝＝，
∴BE＝2BF，
∴AE＝2A'F；
【深入探究】：∵将△ADE沿直线DE折叠后，当点A'恰好落在DF上时，
∴AE＝A'E，∠A＝∠DA'E＝90°，
∴∠B＝∠EA'F＝90°，
∵∠AED+∠BEF＝90°＝∠DEA'+∠FEA'，
∴∠BEF＝∠FEA'，
又∵EF＝EF，
∴△BEF≌△A'EF（AAS），
∴BE＝A'E＝AE＝AB，A'F＝BF，
∵AD＝mAB，
∴AE＝AD，
∵∠AED+∠BEF＝90°＝∠AED+∠ADE，
∴∠BEF＝∠ADE，
∴tan∠ADE＝tan∠BEF＝＝，
∴BE＝2mBF，
∴AE＝2mA'F；
【拓展探究】：如图4，在BE上截取BF＝BN，连接NF，在A'F上截取FH＝FN，连接EH，
∵四边形ABCD是菱形，∠B＝60°，
∴AB＝AD，∠A＝120°，
∵∠B＝60°，BF＝BN，
∴△BNF是等边三角形，
∴BN＝BF＝NF，∠B＝∠BFN＝∠BNF＝60°，
∴∠ENF＝120°，
设∠BEF＝x，
∵∠DEF＝∠A＝120°，∠B＝60°，
∴∠BFE＝120°﹣x，∠AED＝60﹣x，
∴∠NFE＝60°﹣x，
∵∠DEB＝∠A+∠ADE＝∠DEF+∠BEF，
∴∠ADE＝∠BEF＝x，
∵将△ADE沿直线DE折叠后，当点A'恰好落在DF上时，
∴AE＝A'E，∠A＝∠DA'E＝120°，∠ADE＝∠A'DE＝x，∠DEA＝∠DEA'＝60﹣x，
∴∠EFA'＝60﹣x，
∴∠EFN＝∠EFH，
又∵EF＝EF，FN＝FH，
∴△EFH≌△EFN（SAS），
∴EN＝EH，∠BEF＝∠FEH＝x，
∵∠BEF+∠AED＝60°，
∴∠FEH+∠DEA'＝60°，∴∠A'EH＝60°，
又∵∠EA'H＝180°﹣∠EA'D＝60°，
∴△A'EH是等边三角形，
∴A'E＝EH＝A'H，
∴设AE＝a＝A'E＝A'H＝EH＝EN，BN＝b，
∴AB＝2a+b＝AD＝A'D，
∵∠A'DE＝∠FEH＝x，∠EFH＝∠DEA'＝60°﹣x，
∴△DEA'∽△EFH，
∴＝，∴，
∴a＝b+b，（负值舍去），
∴AE＝b+b，A'F＝a+b＝2b+b，
∴A'F＝AE．
又∵AE＝2，∴A'F＝4．