2022-2023学年湖北省武汉市东西湖区辛安渡中心小学人教版六年级下册期末模拟测试 数学试卷答案

这是一份2022-2023学年湖北省武汉市东西湖区辛安渡中心小学人教版六年级下册期末模拟测试 数学试卷答案，共19页。试卷主要包含了选择题，判断题，填空题，计算题，图形题，解决问题等内容，欢迎下载使用。
一、选择题。（每小题2分，共10分。）
1. 为统计实验小学各年级学生人数同学生总人数的关系，应选择（ ）统计图比较合适。
A. 条形统计图B. 折线统计图C. 扇形统计图D. 无法确定
【答案】C
【解析】
【分析】条形统计图可以清楚地看出数量的多少；
折线统计图不但可以表示出数量的多少，而且能够清楚地表示出数量增减变化的情况；
扇形统计图表示各部分数量与总数之间的关系。
【详解】为统计实验小学各年级学生人数同学生总人数的关系，应选择扇形统计图统计图比较合适。
故答案为：C
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
2. 下列计算方法正确的是（ ）。
A. 36＋127＝（1＋3）×100＋（2＋6）×10＋7×1B. 3.2＋0.32＝（3＋3）×0.1＋（2＋2）×0.01
C. ＋＝（1＋3）×D. ＋＝（1＋3）×
【答案】D
【解析】
【分析】将各选项左右两边的算式分别计算出来，再比较结果是否一致即可。
【详解】A．36＋127＝163
（1＋3）×100＋（2＋6）×10＋7×1
＝400＋80＋7
＝487
左边不等于右边
B．3.2＋0.32＝3.52
（3＋3）×0.1＋（2＋2）×0.01
＝0.6＋0.04
＝0.64
左边不等于右边
C．＋＝
（1＋3）×
＝4×
＝
左边不等于右边
D．＋＝
（1＋3）×
＝4×
＝
左边等于右边
故答案为：D
【点睛】计算出各选项左右两边算式是否相等是解答的关键。
3. 导演让一位木偶演员操纵木偶做下面的动作：

开始 结束
中间每个图形分别是通过（ ）得到。
A. 旋转、旋转、旋转、平移B. 旋转、平移、旋转、平移
C. 旋转、旋转、平移、平移D. 平移、旋转、旋转、平移
【答案】A
【解析】
【分析】在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。
在平面内，将一个图形沿着某个方向移动一定的距离，这样的运动叫做图形的平移。
【详解】木偶从“开始”顺时针旋转90°后头朝右，再顺时针旋转90°后头朝下，继续顺时针旋转90°后头朝左，最后向右平移到“结束”。
所以，中间每个图形分别是通过旋转、旋转、旋转、平移得到的。
故答案为：A
【点睛】掌握旋转和平移的特点是解题的关键。
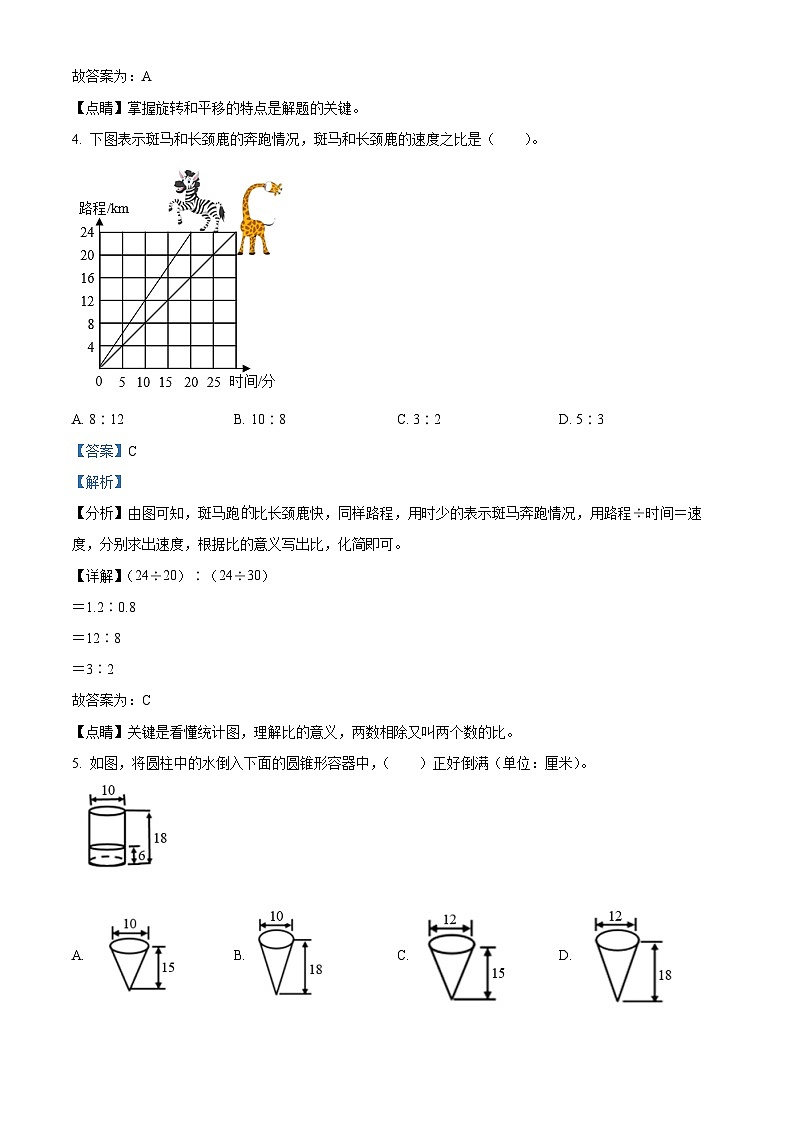
4. 下图表示斑马和长颈鹿的奔跑情况，斑马和长颈鹿的速度之比是（ ）。
A. 8∶12B. 10∶8C. 3∶2D. 5∶3
【答案】C
【解析】
【分析】由图可知，斑马跑比长颈鹿快，同样路程，用时少的表示斑马奔跑情况，用路程÷时间＝速度，分别求出速度，根据比的意义写出比，化简即可。
【详解】（24÷20）∶（24÷30）
＝1.2∶0.8
＝12∶8
＝3∶2
故答案为：C
【点睛】关键是看懂统计图，理解比的意义，两数相除又叫两个数的比。
5. 如图，将圆柱中的水倒入下面的圆锥形容器中，（ ）正好倒满（单位：厘米）。
A. B. C. D.
【答案】B
【解析】
【分析】先根据圆柱的体积求出水的体积；再根据圆锥的体积求出四个选项中圆锥的体积；最后把水的体积和圆锥的体积作比较即可。
【详解】×（10÷2）2×6
＝×52×6
＝×25×6
＝150（立方厘米）
A．×（10÷2）2×15×
＝×52×15×
＝×25×15×
＝125（立方厘米）
125≠150，A选项错误。
B．×（10÷2）2×18×
＝×52×18×
＝×25×18×
＝150（立方厘米）
150＝150，B选项正确。
C．×（12÷2）2×15×
＝×62×15×
＝×36×15×
＝180（立方厘米）
180≠150，C选项错误。
D．×（12÷2）2×18×
＝×62×18×
＝×36×18×
＝216（立方厘米）
216≠150，D选项错误。
故答案为：B
【点睛】此题考查了圆柱和圆锥的体积计算公式。等底等体积的圆锥的高是圆柱的高的3倍。
二、判断题。（每小题1分，共5分。）
6. 质数都是奇数，合数都是偶数。（ ）
【答案】×
【解析】
【分析】根据质数、合数、奇数、偶数的意义解答，找出反例证明。
【详解】2是质数但是2不是奇数，9是合数但是9不是偶数，所以质数都是奇数，合数都是偶数的说法是错误的。
故答案为：×
【点睛】本题主要考查质数、合数、奇数、偶数的意义。
7. 以直角三角形任意一边为轴旋转一周，都可以得到一个圆锥。（ ）
【答案】×
【解析】
【分析】以直角三角形任意一条直角边旋转一周，都可以得到一个圆锥体。
【详解】任何一个直角三角形以任意一条直角边为轴旋转一周，都可以得到一个圆锥，而不是任意一边，当它以斜边旋转一周时得到的就不是圆锥体了，本题结论是错误的。
故答案为：×
【点睛】本题主要考查学生在做图形旋转题的时候，要缜密思路每一种可能性，不要盲目下结论。
8. 植树节种植了101棵树苗全部存活，这批树苗的存活率是101%。（ ）
【答案】×
【解析】
【分析】存活率＝存活的棵数÷总棵数，存活率等于或小于100%。
【详解】101÷101×100%
＝1×100%
＝100%
原题说法错误。
故答案为：×
【点睛】了解存活率的意义是解答的关键。
9. 比90°大的角都是钝角。（ ）
【答案】×
【解析】
【分析】大于90°小于180°的角，叫做钝角；据此解答即可。
【详解】根据钝角的含义可知：比90°大的角都是钝角，说法错误，如：180°；
故答案为：×
【点睛】明确钝角的含义，是解答此题的关键。
10. 小明家门前的小河平均水深1.1米，小明身高1.2米，他不会游泳，但他下河玩耍肯定安全。（ ）
【答案】×
【解析】
【分析】平均数是反映一组数据的平均水平，并不能反映这组数据中各个数据的大小，据此解答。
【详解】一条小河平均水深1.1米，并不能反映出整个小河中每一处的水深大小，有的地方会深一些，有的地方会浅一些，所以身高1 .2米的小明要过河会有危险。
故答案：×
【点睛】此题考查了平均数的意义在实际生活中的灵活应用。
三、填空题。（每小题2分，共16分。）
11. 2022年北京冬奥会其间，共有一万七千四百七十二条相关热搜登上热搜榜，这个数写作（ ），改写成用“万”作单位的数是（ ）万。
【答案】 ①. 17472 ②. 1.7472
【解析】
【分析】整数的写法：从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0。
改写时，如果不是整万的数，要在万位的后边，点上小数点，去掉小数点末尾的0，并加上一个“万”字。
【详解】一万七千四百七十二，写作：17472；17472＝1.7472万
2022年北京冬奥会其间，共有一万七千四百七十二条相关热搜登上热搜榜，这个数写作17472，改写成用“万”作单位的数是1.7472万。
【点睛】关键是掌握整数的写法，改写后的整数与原数相等，用等号＝连接。
12. 3.05公顷＝（ ）平方米 2.25时＝（ ）时（ ）分
【答案】 ①. 30500 ②. 2 ③. 15
【解析】
【分析】3.05公顷转化为平方米，是大单位变为小单位，乘进率10000；0.25时转化为分，是大单位变为小单位，乘进率60。
【详解】3.05公顷＝3.05×10000＝30500（平方米）
3.05公顷＝（30500）平方米
0.25时＝0.25×60＝15（分）
2.25时＝（2）时（15）分
【点睛】掌握不同单位之间的进率及转化方向，采用合适的计算方法是解答的关键。
13. 3270千克雪梨需要装箱运输，每80千克装一箱，大约需要（ ）个箱子。
【答案】41
【解析】
【分析】要将3270千克雪梨分装在每箱可盛80千克的箱子里，求需要准备几个箱子，就是求3270里面有几个80，用除法计算。计算的结果按“进一法”取整数。
【详解】3270÷80≈41（个）
所以大约需要41个箱子。
【点睛】在现实生活中，求至少需要几辆车才能运完，到少需要几个箱子才能装下，至少需要几个瓶子等问题，应采用“进一法”。
14. 一种贺卡的单价是a元，小明买n张这样的贺卡，付出10元，应找回（ ）元。如果a＝0.75，n＝5，则实际找回（ ）元。
【答案】 ①. 10－an ②. 6.25
【解析】
【分析】单价×数量＝总价，付的钱数－贺卡单价×买的张数＝找回的钱数，据此用字母表示出找回的钱数，将a＝0.75，n＝5，代入字母表示的算式，求值，是实际找回的钱数。
【详解】10－a×n＝（10－an）元
10－an
＝10－0.75×5
＝10－3.75
＝6.25（元）
一种贺卡的单价是a元，小明买n张这样的贺卡，付出10元，应找回（10－an）元。如果a＝0.75，n＝5，则实际找回6.25元。
【点睛】关键是理解字母可以表示任意数，可以用字母将数量关系表示出来。
15. 在一幅地图上的比例尺如图，将它转化为数值比例尺是（ ）。
【答案】1∶3500000
【解析】
【分析】从线段比例尺可知，图上1厘米相当于实际距离35千米，根据“比例尺＝图上距离∶实际距离”，以及进率“1千米＝100000厘米”，将线段比例尺转化为数值比例尺。
【详解】1厘米∶35千米
＝1厘米∶（35×100000）厘米
＝1∶3500000
将它转化为数值比例尺是1∶3500000。
【点睛】本题考查比例尺的意义以及长度单位的换算，掌握线段比例尺与数值比例尺的互化是解题的关键。
16. 给一个半圆形的花坛边安装围栏，已知花坛的直径是8米，需要准备（ ）米的围栏。
【答案】20.56
【解析】
【分析】由题意知：给一个半圆形的花坛边安装围栏，围栏的周长等于半圆的直径＋圆周长的一半。据此解答。
【详解】8×3.14÷2＋8
＝12.56＋8
＝20.56（米）
，需要准备（20.56）米围栏。
【点睛】掌握半圆周长计算方法是解答的关键。
17. 一个直角三角形，三条边分别为6厘米、8厘米、10厘米，它斜边上的高是（ ）。
【答案】4.8厘米##4.8cm
【解析】
【分析】在一个直角三角形中，斜边最长，即斜边是10厘米，两条直角边分别是6厘米，8厘米；因为“三角形的面积＝底×高÷2”，根据两条直角边计算出三角形的面积；再根据高＝面积×2÷底，代入数据，求出斜边上的高，据此解答。
【详解】6×8÷2×2÷10
＝48÷2×2÷10
＝24×2÷10
＝48÷10
＝4.8（厘米）
一个直角三角形，三条边分别为6厘米、8厘米、10厘米，它斜边上的高是4.8厘米。
【点睛】熟练掌握和灵活运用三角形面积公式是解答本题的关键。
18. 将一个圆柱的侧面展开后得到一个边长是12.56cm的正方形，这个圆柱的表面积是（ ）。
【答案】182.8736cm2##182.8736平方厘米
【解析】
【分析】圆柱的侧面展开后得到一个正方形，说明圆柱底面周长＝高，先求出底面半径，根据圆柱表面积＝底面积×2＋侧面积，列式计算即可。
【详解】12.56÷3.14÷2＝2（cm）
3.14×22×2＋12.56×12.56
＝3.14×4×2＋157.7536
＝25.12＋157.7536
＝182.8736（cm2）
这个圆柱的表面积是182.8736cm2。
【点睛】关键是熟悉圆柱特征，掌握并灵活运用圆柱表面积公式。
四、计算题。（共34分）
19. 直接写出得数。
19.8－1.98＝ 2.4×0.5＝ ＋＝ 36＋74＝
＝ 0.27×＝ 12.6÷3＝ ＝
3.2＋6.8×0＝ 1.25×8÷1.25×8＝
【答案】17.82；1.2；；110
；0.06；4.2；2
3.2；64
【解析】
20. 解方程。
4＋0.7x＝102 x－x＝
2（x－4.5）＝43 x∶＝6∶7
【答案】x＝140；
x＝26；
【解析】
【分析】4＋0.7x＝102，等式两边同时减4，再同时除以0.7，方程得解；x－x＝，化简方程得，等式两边同时除以，方程得解；2（x－4.5）＝43，等式两边同时除以2，再同时加4.5，方程得解；x∶＝6∶7，根据比例的基本性质，转化为方程，等式两边同时除以7，方程得解。
【详解】4＋0.7x＝102
解：4＋0.7x－4＝102－4
0.7x＝98
0.7x÷0.7＝98÷0.7
x＝140
x－x＝
解：

2（x－45）＝43
解：2（x－4.5）÷2＝43÷2
x－4.5＝21.5
x－4.5＋4.5＝21.5＋4.5
x＝26
x∶＝6∶7
解：
21. 计算下列各题。
9405－2940÷28×21 10.5×（3.8－0.8）÷6.3
÷[（－）×] 2023×
【答案】7200；5
；
【解析】
【分析】（1）先算除法，再算乘法，最后算减法；
（2）先算括号里面的减法，再从左往右依次计算；
（3）先算小括号里面的减法，再算中括号里面的乘法，最后算中括号外面的除法；
（4）先把2023分解成2022＋1，然后根据乘法分配律（a＋b）×c＝a×c＋b×c进行简算。
【详解】（1）9405－2940÷28×21
＝9405－105×21
＝9405－2205
＝7200
（2）10.5×（3.8－0.8）÷6.3
＝10.5×3÷6.3
＝31.5÷6.3
＝5
（3）÷[（－）×]
＝÷[（－）×]
＝÷[×]
＝÷
＝×
＝
（4）2023×
＝（2022＋1）×
＝2022×＋1×
＝2021＋
＝
五、图形题。（共10分）
22. 求下面图形的体积。（单位：厘米）

【答案】235.5立方厘米
【解析】
【分析】由图知：圆锥的底面直径是10厘米，半径就是5厘米，高是9厘米，圆锥的体积＝底面积×高×，将数据代入即可求得圆锥的体积。
【详解】
＝3.14×25×3
＝78.5×3
＝235.5（立方厘米）
图形的体积是235.5立方厘米。
23. 求阴影部分的面积。（单位：cm）

【答案】24.5cm2
【解析】
【分析】阴影部分的面积＝两个正方形面积和－两个三角形面积，正方形面积＝边长×边长，三角形面积＝底×高÷2，据此列式计算。
【详解】8×8＋5×5－8×8÷2－（8＋5）×5÷2
＝64＋25－32－13×5÷2
＝57－32.5
＝24.5（cm2）
六、解决问题。（共25分）
24. 修一段路，上午修了80米，下午修的比上午的还多15米，这一天一共修路多少米？
【答案】155米
【解析】
【分析】把上午修路的长度看作单位“1”，根据分数乘法的意义，求一个数的几分之几是多少，用乘法，用上午修路的长度乘，再加上15米，即可求出下午修路的长度，最后加上上午修路的长度，求出这一天一共修路多少米。
【详解】80×＋15＋80
＝60＋15＋80
＝155（米）
答：这一天一共修路155米。
【点睛】此题的解题关键是理解分数乘法的意义，掌握求一个数的几分之几是多少的计算方法，从而解决问题。
25. 红星小学对全校同学进行最喜欢的运动项目调查，调查情况具体如图，其中150名同学喜欢羽毛球，喜欢跳绳的同学有多少名？
【答案】80名
【解析】
【详解】150÷37.5%＝400（名）
400×20%＝80（名）
答：喜欢跳绳的同学有80名。
26. “万达”修路队修筑一条公路，原计划每天修400米，15天可以修完。结果12天就完成了任务，实际每天修多少米？
【答案】500米
【解析】
【分析】工作效率×工作时间＝工作总量，工作总量÷工作时间＝工作效率。将数据代入即可求得实际每天修多少米。据此解答。
【详解】400×15÷12
＝6000÷12
＝500（米）
答：实际每天修500米。
【点睛】灵活运用“工作效率、工作时间、工作总量”三者之间的关系是解答的关键。
27. 有一根铁丝，第一次用去它的一半多1米，第二次用去余下的少1米，这时还剩下15米。求这根铁丝原来长多少米？
【答案】44米
【解析】
【分析】如图，先将第一次用后余下长度看作单位“1”，剩下的15米减去1米刚好是第一次用后余下长度的（1－），根据部分数量÷对应分率＝整体数量，求出第一次用后余下长度；再将铁丝原来长度看作单位“1”，第一次用后余下长度加上1米，刚好是铁丝原来长度的（1－），再根据部分数量÷对应分率＝整体数量，即可求出铁丝原来长度。
【详解】（15－1）÷（1－）
＝14÷
＝14×
＝21（米）
（21＋1）÷（1－）
＝22÷
＝22×2
＝44（米）
答：这根铁丝原来长44米。
【点睛】关键是确定单位“1”，理解分数除法的意义。
28. 杨师傅三天完成一批零件的加工任务。第一天加工的零件数与总零件数的比是3∶8，第二天加工了85个零件，前两天加工的零件数正好占零件总数的。杨师傅第一天加工了多少个零件？
【答案】153个
【解析】
【分析】将总零件数看作单位“1”，第一天加工的零件数与总零件数的比是3∶8，第一天加工的零件数占零件总数的，前两天加工的零件数的对应分率－第一天加工的零件数的对应分率＝第二天加工的零件数的对应分率，第二天加工个数÷对应分率＝总零件数，总零件数×第一天加工的对应分率＝第一天加工的零件数，据此列式解答。
【详解】85÷（－）
＝85÷
＝85×
＝408（个）
408×＝153（个）
答：杨师傅第一天加工了153个零件。
【点睛】关键是确定单位“1”，理解比和分数乘除法的意义。
七、填空题。（每小题4分，共8分。）
29. 计算9.6－11÷9＋×2的结果得（ ）。
【答案】8.6
【解析】
【分析】9.6－11÷9＋×2，同时算出除法和乘法，再添括号，括号前边是减号，添上括号，括号里的加号变减号，进而先算小括号里的，再算括号外的。
【详解】9.6－11÷9＋×2
＝9.6－＋
＝9.6－（－）
＝9.6－1
＝8.6
计算9.6－11÷9＋×2的结果得8.6。
【点睛】整数四则混合运算的运算顺序和简便计算方法同样适用于分数和小数。
30. 如图，A、B是圆直径的两端，甲在A点，乙在B点，同时出发，反向而行。两人在C点第一次相遇，在D点第二次相遇。已知C点离A点有40米，D点离B点有20米，则这个圆的周长是（ ）米。
【答案】200
【解析】
【分析】如图，第一次相遇于C点，距A点40米，此时甲行40米，甲乙共行圆的半个周长，即每行半周甲就行40米。第二次相遇于D点，此时两人共行1周半即3个半周，则甲一共走了40×3＝120米，D点距B点20米，即此时甲行的路程比半周多20米，那么圆的半周长为120－20＝100米，周长为100×2＝200米。
【详解】（40×3－20）×2
＝（120－20）×2
＝100×2
＝200（米）
【点睛】完成本题的关键是根据两次相遇点C、D距A、B两点的距离求出两次相遇时甲行的路程是多少。
八、图形题。（共6分）
31. 如图，阴影部分的面积是60平方厘米，求环形的面积。
【答案】188.4平方厘米
【解析】
【分析】通过观察图形可知，阴影部分的面积等于大小圆半径平方的差，如图所示，设大圆的半径为R，小圆的半径为r，则图中大正方形的边长为R，小正方形的边长为r，则阴影部分的面积＝R2－r2，而阴影部分的面积已知，则可以求出（R2－r2）的值；根据环形面积公式： S＝（R2－r2），把数据代入公式解答。
【详解】设大圆的半径为R，小圆的半径为r，则图中大正方形的边长为R，小正方形的边长为r，因为阴影部分的面积＝R2－r2＝60平方厘米，所以圆环的面积＝大圆的面积－圆的面积：
3.14×60＝188.4（平方厘米）
所以，环形面积是188.4平方厘米。
九、解决问题。（共6分）
32. 一个盒子里有黑棋子和白棋子各若干粒，若取出一粒黑棋子，则余下的黑棋子数与白棋子数之比是9∶7，若放回黑棋子，再取出一粒白棋子，则黑棋子数与余下的白棋子数的比是7∶5，那么盒子里原有的黑棋子数比白棋子数多几粒？
【答案】7粒
【解析】
【分析】我们运用比例进行解答，设白子有x个，黑子是x＋1．用黑子的个数与白子的个数减去1个的比是7：5，列方程进行解答即可。
【详解】解：设白子有x个，黑子是x＋1。
（x＋1）：（x﹣1）＝7：5
x×5＋5＝7x﹣7
6x＋5＝7x﹣7
x＝12
x×＝12×
x＝21
黑子的个数：
x＝×21＋1＝28
28﹣21＝7（个）
答：盒子里原有的黑棋子数比白棋子数多7粒。
【点睛】本题把一个数设为x，再用未知数表示另一个数，进一步列方程解答即可。