（期末典型真题）作图题-广东省深圳市2023-2024学年五年级上册数学期末真题精选（北师大版）

这是一份（期末典型真题）作图题-广东省深圳市2023-2024学年五年级上册数学期末真题精选（北师大版），共31页。试卷主要包含了画出图形A的对称轴，观察下图按要求画一画，按要求画出平移后的图形，按要求画一画等内容，欢迎下载使用。
试卷说明：本试卷试题精选自广东省深圳市近两年五年级上学期期末真题试卷，难易度均衡，适合广东省深圳市及使用北师大版教材的五年级学生期末复习备考使用！
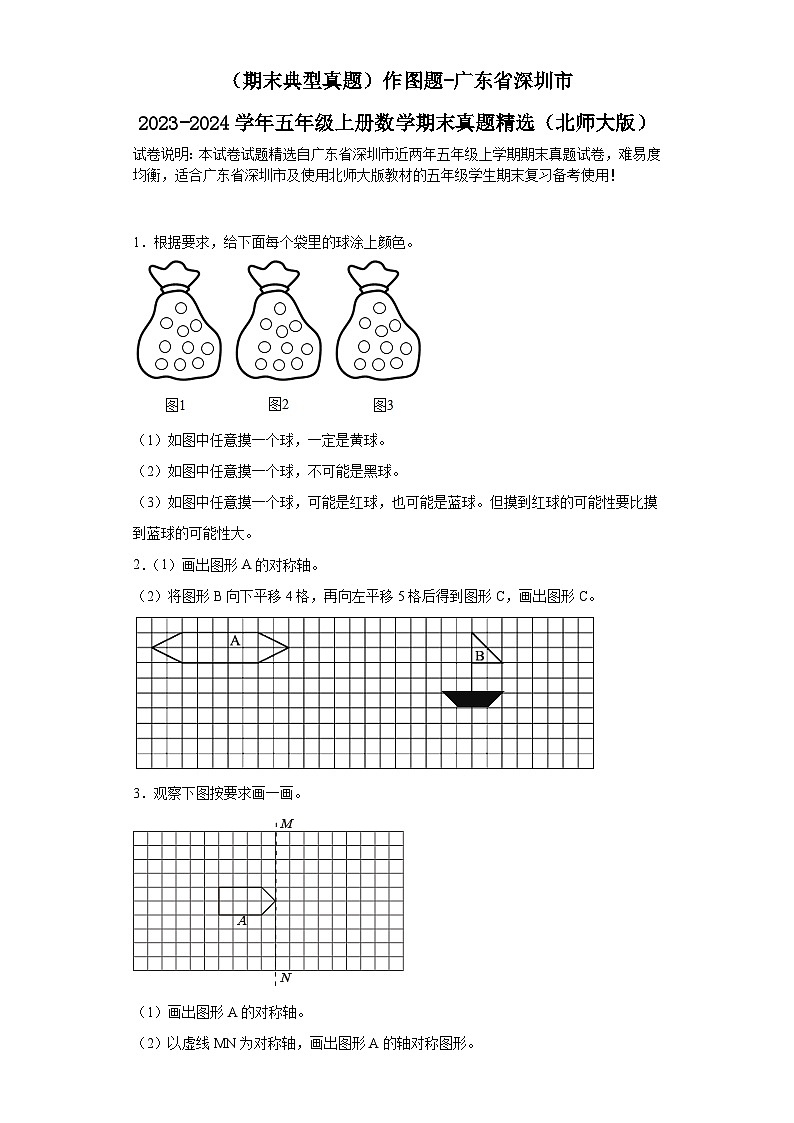
1．根据要求，给下面每个袋里的球涂上颜色。
（1）如图中任意摸一个球，一定是黄球。
（2）如图中任意摸一个球，不可能是黑球。
（3）如图中任意摸一个球，可能是红球，也可能是蓝球。但摸到红球的可能性要比摸到蓝球的可能性大。
2．（1）画出图形A的对称轴。
（2）将图形B向下平移4格，再向左平移5格后得到图形C，画出图形C。
3．观察下图按要求画一画。
（1）画出图形A的对称轴。
（2）以虚线MN为对称轴，画出图形A的轴对称图形。
（3）画出图形A先向上平移3格，再向右平移5格后的图形。
4．按要求画出平移后的图形．
5．根据对称轴画出下面轴对称图形的另一半。
6．在下面的方格纸上（每个小方格的面积都是1cm2），分别画出面积都是12cm2的平行四边形、三角形和梯形。
7．从盒子里任意摸出一个球，按要求给盒子里的球涂色。
8．下面方格图中，每个小方格的面积表示1cm2，请你画出一个三角形，一个平行四边形，一个梯形，使它们的面积都是8cm²。
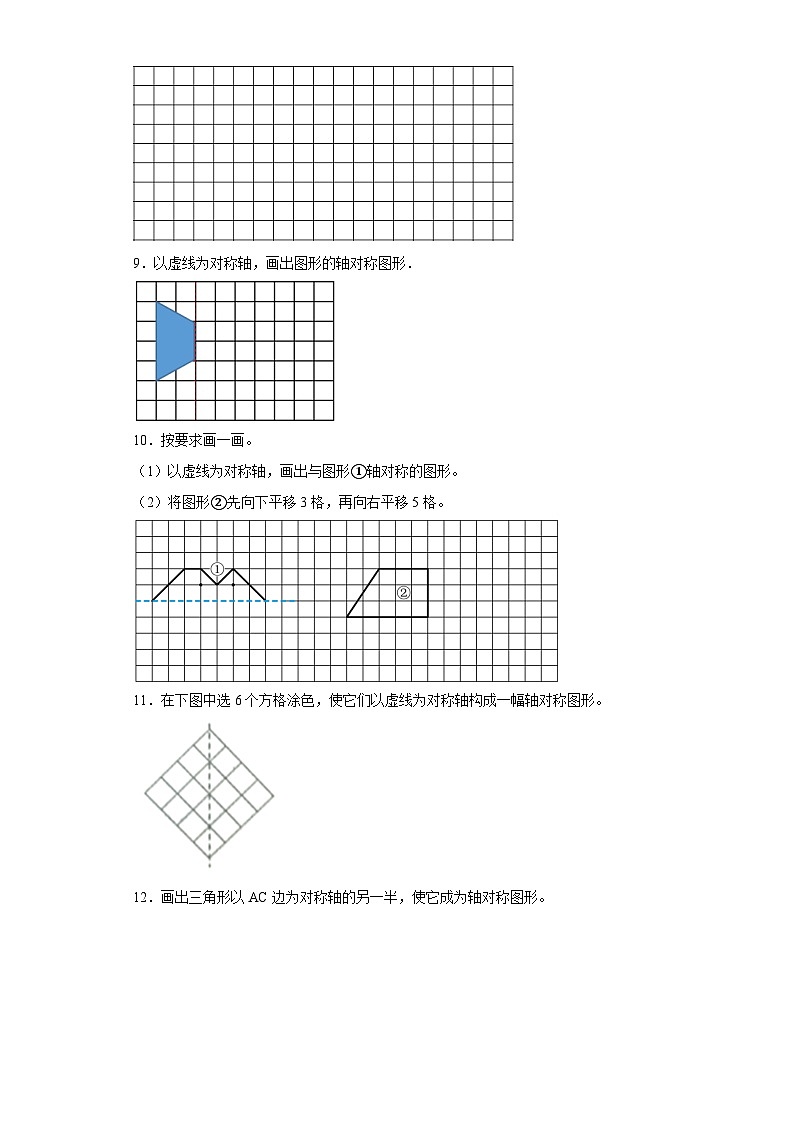
9．以虚线为对称轴，画出图形的轴对称图形．
10．按要求画一画。
（1）以虚线为对称轴，画出与图形①轴对称的图形。
（2）将图形②先向下平移3格，再向右平移5格。
11．在下图中选6个方格涂色，使它们以虚线为对称轴构成一幅轴对称图形。
12．画出三角形以AC边为对称轴的另一半，使它成为轴对称图形。
13．如图，以虚线为对称轴，画出图形的轴对称图形。
14．三名同学玩转盘游戏，转到1是甲赢，转到2是乙赢，转到3是丙赢。请你把数字填入适当的位置，使得这是一个公平的转盘游戏。
15．在每个圆盘上按要求涂色。
（1）转到红色的可能性大， 转到黄色的可能性小。
（2）转到黄色的可能性大，转到红色的可能性小。
（3）转到红色和黄色的可能性同样大。
16．将图形A向右平移8格得到图形B，再以直线l为对称轴作图形B的轴对称图形C．
17．请画出对称图形的另一半。


18．（1）以虚线为对称轴，画出下图的轴对称图形。
（2）画出下图的“石凳”先向上平移2格，再向右平移6格后的图形。
19．按要求画一画。
（1）在方格纸中把图A向右平移5格，再向下平移3格得到图形B。
（2）以虚线为对称轴，画出图形B的轴对称图形得到图形C。
20．画出下面各图形的一条对称轴。

21．利用图形的对称设计图案。
22．图中的三角形先向右平移7格，再向下平移5格，画出最后的图形．
23．在下面每个盒子里放4个球，按照对应的要求，画一画。
24．（1）画出如图梯形的高。
（2）测量出计算梯形面积所需的数据，并在图中标出测量的结果。（测量结果取整厘米数）
（3）计算梯形的面积。
25．按给出的对称轴画出第一个图形的轴对称图形，第二个图形请向上移动4格，再向右移动2格。
26．以虚线为对称轴，画出图形的轴对称图形。
27．按要求画出三角形平移后的图形。说一说原来的平行四边形变成了什么样的图形？
28．在下面方格纸上分别画出下面各图形。（每个小方格的边长是1厘米）
①上底是2厘米，下底是3厘米，面积是10平方厘米的梯形。
②一个腰长等于4厘米的等腰直角三角形。
29．以虚线为对称轴，画出下面图形的轴对称图形。
30．
（1）在如图所示的方格图中画出一个与长方形面积相等的三角形。
（2）图形是向上平移4格后得到的图形，请画出原图。
31．画出下列图形的对称轴。
32．将方格中的图形向右平移两个格．
33．画出下面图形的另一半，使它成为一个轴对称图形。

34．按要求画一画。
（1）画出小鱼先向下平移3格，再向右平移3格后的图形。
（2）画出小船先向左平移7格，再向上平移2格后的图形。
35．根据对称轴画出轴对称图形的另外一半。
36．在下面的方格纸上画出一个三角形、一个梯形、一个平行四边形和一个长方形，使它们的面积都是6平方厘米．（每个小方格表示1平方厘米）
37．按要求画一画。
以虚线为对称轴，画出下列图形的轴对称图形。
38．按要求画一画。
（1）以虚线为对称轴，画出图形①的另一半。
（2）将图形②先向右平移8格，再向上平移3格。
（3）如果每个小方格的边长表示1厘米，画出一个与图形②面积相等的平行四边形。
39．以虚线为对称轴画出图形的另一半，再将画好的轴对称图形向右平移8格。
40．按要求画一画。
（1）画出图形①的所有对称轴。
（2）将图形②先向右平移10格，再向上平移3格。
（3）将图形③先向下平移5格，再向左平移6格。
41．利用平移设计图案．
42．请在方格纸上以AB为底，画出面积是9平方厘米的直角三角形、钝角三角形。（每格边长1厘米）
43．请在下面的方格纸中画出一个三角形，一个平行四边形和一个梯形，使他们的面积都是6cm2．（每个方格表示1cm2）
44．按要求画一画．
(1)把图形A先向上平移2格，再向右平移3格．
(2)把图形B先向左平移4格，再向下平移2格．
参考答案：
1．见详解
【分析】（1）全部涂成黄色，摸出的球一定是黄球；
（2）不涂黑色，则任意摸出一个球，不可能是黑球；
（3）任意摸一个球，可能是红球，也可能是蓝球。但摸到红球的可能性要比摸到蓝球的可能性大。则只能涂红色和蓝色，且红色球的个数一定大于蓝色球的个数。
【详解】（1）
（2） （答案不唯一）
（3） （答案不唯一）
此题主要考查学生对可能性知识的熟练掌握与灵活运用。
2．见详解
【分析】（1）根据轴对称图形的意义，对称点到对称轴的距离相等，画图即可。
（2）根据平移的特征，把图形B的各顶点向下平移4格，再向左平移5格，然后连接各顶点即可。
【详解】画图如下：
本题考查轴对称和平移的知识，掌握轴对称的意义和平移只改变位置，图形大小形状完全相同。
3．见详解
【分析】（1）如果一个图形沿着一条虚线对折，两侧的图形完全重合，这个图形叫做轴对称图形，这条虚线叫做对称轴，据此画出图形A的对称轴。
（2）补全轴对称图形的方法：找出图形的关键点，依据对称轴画出关键点的对称点，再依据图形的形状顺次连接各点，画出最终的轴对称图形。
（3）作平移后的图形步骤：1、找出构成图形的关键点；2、确定平移方向和平移距离；3、由平移的距离确定关键点平移后的对应点的位置；4、连接对应点。
【详解】
本题考查画对称轴、补全轴对称图形和作平移后的图形。补全轴对称图形和画平移后的图形时，找出图形的关键点是画图的关键。一般把线段的交点作为关键点。
4．
【解析】略
5．见详解
【分析】找出图形的关键点，依据对称轴画出关键点的对称点，再依据图形的形状顺次连接各点，画出最终的轴对称图形。
【详解】
本题考查的是补全轴对称图形，找到关键点，做出关键点的对称点是关键。
6．见详解
【分析】平行四边形、三角形和梯形的面积都已知，且都相等，根据平行四边形、三角形和梯形的面积公式，于是可以分别确定出平行四边形的底和高、三角形的底和高以及梯形的上底、下底和高的值，进而就可以在方格图中画出这几个图形。
【详解】因为S平行四边形＝S三角形＝S梯形＝12平方厘米，
所以平行四边形的底和高为4厘米和3厘米，
三角形的底和高为6厘米和4厘米，
梯形的上底、下底和高为3厘米、5厘米和3厘米，
作图如下：
此题主要考查平行四边形、三角形和梯形的面积的计算方法的灵活应用，关键是先确定出计算这几个图形的面积所需要的主要线段的长度，进而完成画图。
7．见详解
【分析】（1）一定摸到黑球，那么盒子里都是黑球即可；
（2）白球的数量大于黑球的数量即可；
（3）黑球的数量大于白球的数量即可。
【详解】根据分析可知：
（后两个答案不唯一）
此题考查了事件的确定性和不确定性，注意应结合题意进行涂色。
8．见详解
【分析】三角形的面积＝底×高÷2，三角形的底和高分别取4厘米画图即可；平行四边形的面积＝底×高，平行四边形的底和高分别取4厘米、2厘米画图即可；梯形的面积＝（上底＋下底）×高÷2，梯形的上底取3厘米、下底取5厘米、高取2厘米画图即可。
【详解】由分析画图如下：
（答案不唯一）
本题主要考查画指定面积的平面图形，牢记三角形、平行四边形、梯形的面积公式是解题的关键。
9．
【解析】略
10．见详解
【分析】（1）先找到顶点，再找到对称点，最后描点连线即可画出对称图形的另一半；
（2）把平移的图形的各个顶点按照指定的方向和格数平移到新的位置，再把各点按原图顺序连接起来；即可画出图形。
【详解】
掌握画轴对称图形和平移后图形的方法是解题的关键。
11．见详解
【分析】一个图形沿一条直线对折后直线两边能够完全重合，这个图形就是轴对称图形，这条直线就是对称图形的对称轴，据此解答。
【详解】画图如下：
（画法不唯一）
此题考查了轴对称图形的画法，根据对称轴的位置认真作图即可。
12．见详解
【分析】根据轴对称的定义，结合题意，直接作图即可。
【详解】
本题考查了轴对称，明确轴对称图形的作图方法是作图的关键。
13．见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，找出所给图形关键点的对称点，依次连接即可。
【详解】如图所示：
此题考查了作对称图形，关键是确定对称点的位置。
14．见详解
【分析】只要1、2、3三个数的个数相同，游戏就公平，否则就不公平。
【详解】如图：
转盘平均分为6块，三名同学玩游戏，每个数字数量为2个即为公平；如图：
根据游戏的公平性原则，解答此题即可。
15．见详解
【分析】（1）要使转到红色的可能性大，转到黄色的可能性小，只要涂红色部分多于涂黄色的部分即可；
（2）要使转到黄色的可能性大，转到红色的可能性小，只要涂黄色部分多于涂红色的部分即可；
（3）要使转到红色和黄色的可能性同样大，只要涂红色部分和涂黄色的部分一样多即可。
【详解】按要求涂色如下：
（1）
（2）
（3）
此题考查可能性大小的比较：只要总情况数目相同，谁包含的情况数目多，谁的可能性就大；反之也成立；若包含的情况相当，那么它们的可能性就相等。
16．
【详解】略
17．；
【解析】略
18．见详解
【分析】（1）根据轴对称图形的特点和性质，每组对应点到对称轴的距离相等，每组对应点的连线垂直于对称轴，先描出每组对应点，然后顺次用直线连接各点即可；
（2）根据平移的特征，把图中的各顶点分别向上平移2格，再向右平移6格，依次连结即平移后的图形。
【详解】（1）以虚线为对称轴，画出的轴对称图形（下图1所示）；
（2）“石凳”先向上平移2格，再向右平移6格后的图形（下图2所示）。
求作一个几何图形关于某条直线对称的图形，可以转化为求作这个图形上的特征点关于这条直线对称的点，然后依次连结各对称点即可；平移作图要注意：①方向；②距离，整个平移作图，就是把整个图案的每一个特征点按一定方向和一定的距离平行移动。
19．（1）（2）见详解
【分析】（1）根据平移的特征，把图A各顶点分别向右平移5格，再向下平移3格，之后依次连结各顶点即可得到向右平移5格，再向下平移3格后的图形；
（2）依据补全轴对称图形的画法：找出图形的关键点，依据对称轴画出关键点的对称点，再依据图形的形状顺次连接各点，画出最终的轴对称图形。
【详解】（1）（2）如下图所示：
本题主要考查作平移后的图形以及作轴对称图形的方法，应熟练掌握它们的特征并灵活运用。
20．见详解
【分析】依据轴对称图形的意义及特征，即在平面内，如果一个图形沿一条直线对折，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线就是其对称轴；据此画出其对称轴即可。
【详解】作图如下：

此题主要考查轴对称图形的意义及其对称轴的画法。
21．见详解
【分析】以左边顶点处竖直的线为对称轴，画出原图形的轴对称图形，这样画出设计的图形即可。
【详解】由分析可知画图如下：
此题主要考查运用对称设计图案，掌握画对称图形的方法是解题关键。
22．如图：
【解析】略
23．见详解
【分析】根据题意可知，（1）说明盒子里全部是红球；
（2）说明盒子里没有红球；
（3）说明盒子里的红球个数比黄球多；
（4）说明盒子里的黄球个数比红球少；据此画出图。
【详解】
本题考查可能性大小的知识，关键是根据题意正确画出图。
24．（1）（2）
（3）12平方厘米
【详解】（1）如图所示：
（2）上底为3厘米，下底为5厘米，高为3厘米；
（3）面积为：
（3＋5）×3÷2
＝8×3÷2
＝12（平方厘米）
答：梯形的面积为12平方厘米。
25．见详解
【分析】补全轴对称图形的方法：找出图形的关键点，依据对称轴画出关键点的对称点，再依据图形的形状顺次连接各点，画出最终的轴对称图形。
作平移后的图形步骤：（1）找点－找出构成图形的关键点；（2）定方向、距离－确定平移方向和平移距离；（3）画线－过关键点沿平移方向画出平行线；（4）定点－由平移的距离确定关键点平移后的对应点的位置；（5）连点－连接对应点。
【详解】
26．见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，画出对应点，然后顺次连接各点即可。
【详解】如图：
本题考查轴对称图形，明确作轴对称图形的方法是解题的关键。
27．见详解
【分析】作平移后的图形步骤：
（1）找点，找出构成图形的关键点；
（2）定方向、距离，确定平移方向和平移距离；
（3）画线，过关键点沿平移方向画出平行线；
（4）定点，由平移的距离确定关键点平移后的对应点的位置；
（5）连点，连接对应点。
【详解】
上边的平行四边形变成了长方形，下边的平行四边形变成了正方形。
物体或图形平移后，它们的形状、大小、方向都不改变，只是位置发生了变化。
28．见详解
【分析】①梯形的高：10×2÷（2＋3）＝20÷5＝4（厘米），根据上底、下底和高的长度画图即可。
②画一个两条直角边都是4厘米的直角三角形即可。
【详解】画图如下：
画梯形时需要先计算梯形的高，注意先让梯形面积×2再计算。
29．见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出左边图形的关键对称点，依次连接即可得到轴对称图形。
【详解】
本题考查作轴对称图形，需要熟练掌握。
30．（1）见详解（答案不唯一）；（2）见详解
【分析】（1）根据长方形的面积公式：长×宽可知长方形的面积是4×2＝8，根据三角形的面积公式：底×高÷2，已知面积，则底×高＝面积×2＝8×2＝16，可画底是4，高是4的三角形，答案不唯一。
（2）根据平移图形的特征，把图形的顶点分别向下平移4格，再顺次连接各点即可。
【详解】如图：
本题考查长方形和三角形面积公式的灵活运用以及图形的平移。
31．见详解
【分析】如果一个图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是对称轴，据此即可解答。
【详解】
解答此题的主要依据是轴对称图形的概念，学生应掌握。
32．
【解析】略
33．图形见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，画出对应点，然后顺次连接各点即可。
【详解】如图所示：

本题考查轴对称图形，明确作轴对称图形的方法是解题的关键。
34．（1）（2）见详解
【分析】（1）根据平移的特征，把小鱼图形的各个顶点先分别向下平移3格，再向右平移3格，依次连接，即可得平移后的图形；
（2）把小船图形的各个顶点先分别向左平移7个，再向上平移2格，依次连接，即可得到平移后的图形。
【详解】如下图：
本题考查做平移后的图形，我们画平移图形时，要注意平移的方向和距离要准确，平移后图形的形状和大小不发生变化。
35．见详解
【分析】根据轴对称图形的性质，先找到右边图形各关键点的对应点，依次连接各点即可画出图形的另一半，使它成为一个轴对称图形。
【详解】
掌握补全轴对称图形的步骤和方法是解题的关键。
36．
【分析】平行四边形、三角形、梯形和长方形的面积都已知，且都相等，于是可以分别确定出平行四边形的底和高、三角形的底和高以及梯形的上底、下底和高与长方形的长和宽的值，进而就可以在方格图中画出这几个图形．
【详解】因为S平行四边形=S三角形=S梯形=6平方厘米，
则三角形的底和高可以为6厘米和2厘米，
平行四边形的底和高可以为3厘米和2厘米，
梯形的上底、下底和高可以为2厘米、4厘米和2厘米，
长方形的长是3厘米，宽是2厘米．
于是所画图形如下图所示：
37．见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，画出对应点，然后顺次连接各点即可。
【详解】如图所示：
本题考查轴对称图形，明确作轴对称图形的方法是解题的关键。
38．（1）（2）（3）见详解
【分析】（1）根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴（虚线）的右边画出图①的左图的关键对称点，依次连接即可；
（2）根据平移的特征，把图②的各顶点分别向右平移8格，再向上平移3个，依次连接即可得到平移后的图形；
（3）图②的上底是2厘米，下底是4厘米，高是3厘米，根据梯形的面积公式：面积＝（上底＋下底）×高÷2，代入数据，求出这个梯形的面积，（2＋4）×3÷2＝9平方厘米，根据平行四边形面积公式：面积＝底×高，底是3厘米，高是3厘米，画出平行四边形（答案不唯一）。
【详解】（1）（2）见下图；
（3）（2＋4）×3÷2
＝6×3÷2
＝18÷2
＝9（平方厘米）
平行四边形的底是3厘米，高是3厘米。
本题考查作轴对称图形，作平移后的特征，画平行四边形，以及梯形面积公式、平行四边形面积公式的应用。
39．见详解
【分析】（1）根据轴对称图形的性质，找出图中已知图形部分的关键点，再找出这些关键点关于对称轴的对称点，顺次连接即可；
（2）根据平移的特征，将图形的各顶点分别向右平移8格，再把平移后的点依次连接起来即可。
【详解】根据分析作图如下：
此题考查了利用轴对称、平移特点进行图形转换的灵活应用。
40．（1）、（2）、（3）见详解
【分析】（1）根据轴对称图形的性质，对称点到对称轴的距离相等，对称轴是对称点的连线的垂直平分线，在对称轴的另一边画出图形的几个顶点，再依次连线即可；
（2）根据平移的特征，将图形②的各顶点分别向右平移10格，再向上平移3格，最后首尾连接各点即可画出该图形。
（3）根据平移的特征，将图形③的各顶点分别向下平移5格，再向左平移6格，最后首尾连接各点即可画出该图形。
【详解】（1）、（2）、（3）如图：
本题考查了作轴对称图形和作平移后的图形，以上知识都需要熟练掌握并且灵活运用，尤其需要能结合知识准确画图。
41．作出图形，如图所示：
【详解】把此四边形向右平移1格、2格、3格、4格、5格、6格，并保留图象，获得的图案如下图所示，犹如我们学校的大门．
42．见详解
【分析】根据三角形面积计算公式：底×高÷2，以AB为三角形的底，AB＝6厘米，则三角形的高为9×2÷6＝3（厘米），根据直角三角形的意义、钝角三角形的意义即分别画出以AB为底、高为3厘米的直角三角形、钝角三角形（画法不唯一）。
【详解】
本题考查三角形面积公式的应用，根据已知面积画出三角形。
43．
【分析】根据三角形的面积公式“S=ah”，画一个底为4厘米，高为3厘米的三形，其面积是4×3÷2=6（平方厘米）；根据平行四边形的面积公式“S=ah”，画一个底为3厘米，高为2厘米的平行四形，其面积是3×2=6（平方厘米）；根据梯形的面积公式“S=（a+b）h”，画一个上底为2厘米，下底为4厘米，高为2厘米的梯形，其面积是×（2+4）×2=6（平方厘米）．
【详解】在下面的方格纸中画出一个三角形，一个平行四边形和一个梯形，使他们的面积都是6cm2．（每个方格表示1cm2）：
44．(1)(2)如下图．
【详解】略