2020年内蒙古呼伦贝尔市中考数学真题及答案

这是一份2020年内蒙古呼伦贝尔市中考数学真题及答案，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）﹣2020的绝对值是（ ）
A．﹣2020B．2020C．﹣D．
2．（3分）下列计算正确的是（ ）
A．a2•a3＝a6B．（x+y）2＝x2+y2
C．（a5÷a2）2＝a6D．（﹣3xy）2＝9xy2
3．（3分）下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
4．（3分）由5个相同的小正方体组成的几何体如图所示，该几何体的俯视图是（ ）
A．B．
C．D．
5．（3分）下列事件是必然事件的是（ ）
A．任意一个五边形的外角和为540°
B．抛掷一枚均匀的硬币100次，正面朝上的次数为50次
C．13个人参加一个集会，他们中至少有两个人的出生月份是相同的
D．太阳从西方升起
6．（3分）如图，直线AB∥CD，AE⊥CE于点E，若∠EAB＝120°，则∠ECD的度数是（ ）
A．120°B．100°C．150°D．160°
7．（3分）已知实数a在数轴上的对应点位置如图所示，则化简|a﹣1|﹣的结果是（ ）
A．3﹣2aB．﹣1C．1D．2a﹣3
8．（3分）不等式组的非负整数解有（ ）
A．4个B．5个C．6个D．7个
9．（3分）甲、乙两人做某种机械零件，已知甲做240个零件与乙做280个零件所用的时间相等，两人每天共做130个零件．设甲每天做x个零件，下列方程正确的是（ ）
A．＝B．＝
C．+＝130D．﹣130＝
10．（3分）如图，AB＝AC，AB的垂直平分线MN交AC于点D，若∠C＝65°，则∠DBC的度数是（ ）
A．25°B．20°C．30°D．15°
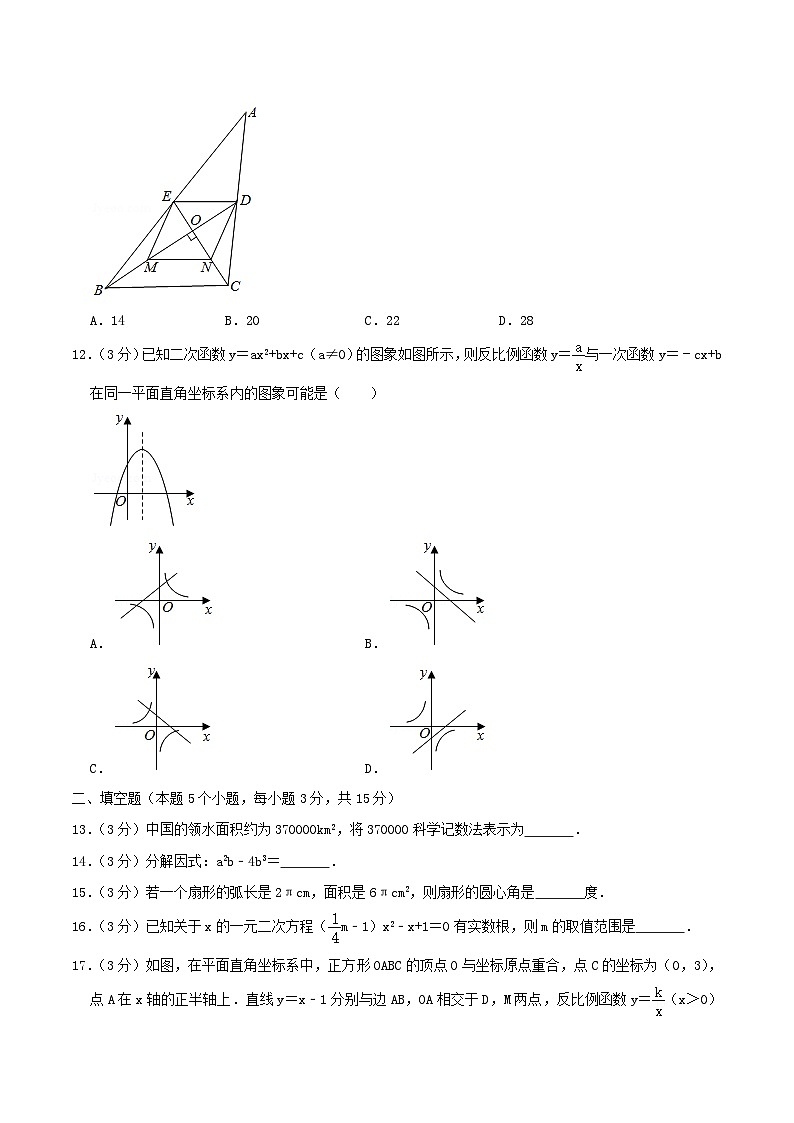
11．（3分）如图，在△ABC中，BD，CE分别是边AC，AB上的中线，BD⊥CE于点O，点M，N分别OB，OC的中点，若OB＝8，OC＝6，则四边形DEMN的周长是（ ）
A．14B．20C．22D．28
12．（3分）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则反比例函数y＝与一次函数y＝﹣cx+b在同一平面直角坐标系内的图象可能是（ ）
A．B．
C．D．
二、填空题（本题5个小题，每小题3分，共15分）
13．（3分）中国的领水面积约为370000km2，将370000科学记数法表示为 ．
14．（3分）分解因式：a2b﹣4b3＝ ．
15．（3分）若一个扇形的弧长是2πcm，面积是6πcm2，则扇形的圆心角是 度．
16．（3分）已知关于x的一元二次方程（m﹣1）x2﹣x+1＝0有实数根，则m的取值范围是 ．
17．（3分）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的正半轴上．直线y＝x﹣1分别与边AB，OA相交于D，M两点，反比例函数y＝（x＞0）的图象经过点D并与边BC相交于点N，连接MN．点P是直线DM上的动点，当CP＝MN时，点P的坐标是 ．
三、解答题（本题4个小题，每小题6分，共24分）
18．（6分）计算：（﹣）﹣1++2cs60°﹣（π﹣1）0．
19．（6分）先化简，再求值：÷+3，其中x＝﹣4．
20．（6分）A，B两地间有一段笔直的高速铁路，长度为100km．某时发生的地震对地面上以点C为圆心，30km为半径的圆形区域内的建筑物有影响．分别从A，B两地处测得点C的方位角如图所示，tanα＝1.776，tanβ＝1.224．高速铁路是否会受到地震的影响？请通过计算说明理由．
21．（6分）一个不透明的口袋中装有三个完全相同的小球，上面分别标有数字，，5．
（1）从口袋中随机摸出一个小球，求摸出小球上的数字是无理数的概率（直接写出结果）；
（2）先从口袋中随机摸出一个小球，将小球上的数字记为x，把小球放回口袋中并搅匀，再从口袋中随机摸出一个小球，将小球上的数字记为y．请用列表法或画树状图法求出x与y的乘积是有理数的概率．
四、（本题7分）
22．（7分）已知：如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F分别是边BC，CD上的点，且∠EOF＝90°．
求证：CE＝DF．
五、（本题7分）
23．（7分）某校为了了解初中学生每天的睡眠时间（单位为小时），随机调查了该校的部分初中学生，根据调查结果，绘制出如图统计图．
请根据相关信息，解答下列问题：
（1）本次接受调查的初中学生人数为 人，扇形统计图中的m＝ ，条形统计图中的n＝ ；
（2）所调查的初中学生每天睡眠时间的众数是 ，方差是 ；
（3）该校共有1600名初中学生，根据样本数据，估计该校初中学生每天睡眠时间不足8小时的人数．
六、（本题8分）
24．（8分）如图，⊙O是△ABC的外接圆，直线EG与⊙O相切于点E，EG∥BC，连接AE交BC于点D．
（1）求证：AE平分∠BAC；
（2）若∠ABC的平分线BF交AD于点F，且DE＝3，DF＝2，求AF的长．
七、（本题10分）
25．（10分）某商店销售一种销售成本为每件40元的玩具，若按每件50元销售，一个月可售出500件，销售价每涨1元，月销量就减少10件．设销售价为每件x元（x≥50），月销量为y件，月销售利润为w元．
（1）写出y与x的函数解析式和w与x的函数解析式；
（2）商店要在月销售成本不超过10000的情况下，使月销售利润达到8000元，销售价应定为每件多少元？
（3）当销售价定为每件多少元时会获得最大利润？求出最大利润．
八、（本题13分）
26．（13分）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）和点B（4，0），与y轴交于点C，连接BC，点P是线段BC上的动点（与点B，C不重合），连接AP并延长AP交抛物线于点Q，连接CQ，BQ，设点Q的横坐标为m．
（1）求抛物线的解析式和点C的坐标；
（2）当△BCQ的面积等于2时，求m的值；
（3）在点P运动过程中，是否存在最大值？若存在，求出最大值；若不存在，请说明理由．
答案
一、选择题（下列各题的四个选项中只有一个正确．共12小题，每小题3分，共36分）
1．参考答案：解：根据绝对值的概念可知：|﹣2020|＝2020，
故选：B．
2．参考答案：解：A、a2•a3＝a5，故选项错误；
B、（x+y）2＝x2+y2+2xy，故选项错误；
C、（a5÷a2）2＝a6，故选项正确；
D、（﹣3xy）2＝9x2y2，故选项错误；
故选：C．
3．参考答案：解：A、不是轴对称图形，是中心对称图形，故此选项错误；
B、是轴对称图形，不是中心对称图形，故此选项错误；
C、既是轴对称图形，也是中心对称图形，故此选项正确；
D、是轴对称图形，不是中心对称图形，故此选项错误；
故选：C．
4．参考答案：解：从上边看第一列是一个小正方形，
第二列是两个小正方形且第一个小正方形位于第一层，
第三列是一个小正方形，且位于第二层，
故B选项符合题意，
故选：B．
5．参考答案：解：A．任意一个五边形的外角和等于540°，属于不可能事件，不合题意；
B．投掷一枚均匀的硬币100次，正面朝上的次数为50次是随机事件，不合题意；
C.13个人参加一个集会，他们中至少有两个人的出生月份是相同的，属于必然事件，符合题意；
D．太阳从西方升起，属于不可能事件，不合题意；
故选：C．
6．参考答案：解：延长AE，与DC的延长线交于点F，
∵AB∥CD，
∴∠A+∠AFC＝180°，
∵∠EAB＝120°，
∴∠AFC＝60°，
∵AE⊥CE，
∴∠AEC＝90°，
而∠AEC＝∠AFC+∠ECF，
∴∠ECF＝∠AEC﹣∠F＝30°，
∴∠ECD＝180°﹣30°＝150°，
故选：C．
7．参考答案：解：由图知：1＜a＜2，
∴a﹣1＞0，a﹣2＜0，
原式＝原式＝a﹣1﹣[﹣（a﹣2）]＝a﹣1+（a﹣2）＝2a﹣3．
故选：D．
8．参考答案：解：，
解不等式①得：x＞﹣2.5，
解不等式②得：x≤4，
∴不等式组的解集为：﹣2.5＜x≤4，
∴不等式组的所有非负整数解是：0，1，2，3，4，共5个，
故选：B．
9．参考答案：解：设甲每天做x个零件，根据题意得：
，
故选：A．
10．参考答案：解：∵AB＝AC，∠C＝∠ABC＝65°，
∴∠A＝180°﹣65°×2＝50°，
∵MN垂直平分AB，
∴AD＝BD，
∴∠A＝∠ABD＝50°，
∴∠DBC＝∠ABC﹣∠ABD＝15°，
故选：D．
11．参考答案：解：∵BD和CE分别是△ABC的中线，
∴DE＝BC，DE∥BC，
∵M和N分别是OB和OC的中点，OB＝8，OC＝6，
∴MN＝BC，MN∥BC，OM＝OB＝4，ON＝OC＝3，
∴四边形MNDE为平行四边形，
∵BD⊥CE，
∴平行四边形MNDE为菱形，
∴BC＝＝10，
∴DE＝MN＝EM＝DN＝5，
∴四边形MNDE的周长为20，
故选：B．
12．参考答案：解：根据二次函数图象与y轴的交点可得c＞0，根据抛物线开口向下可得a＜0，由对称轴在y轴右边可得a、b异号，故b＞0，
则反比例函数的图象在第二、四象限，
一次函数y＝﹣cx+b经过第一、二、四象限，
故选：C．
二、填空题（本题5个小题，每小题3分，共15分）
13．参考答案：解：370000＝3.7×105，
故答案为：3.7×105．
14．参考答案：解：a2b﹣4b3
＝b（a2﹣4b2）
＝b（a+2b）（a﹣2b）．
故答案为b（a+2b）（a﹣2b）．
15．参考答案：解：扇形的面积＝＝6π，
解得：r＝6，
又∵＝2π，
∴n＝60．
故答案为：60．
16．参考答案：解：∵一元二次方程有实数根，
∴△＝≥0且≠0，
解得：m≤5且m≠4，
故答案为：m≤5且m≠4．
17．参考答案：解：∵点C的坐标为（0，3），
∴B（3，3），A（3，0），
∵直线y＝x﹣1分别与边AB，OA相交于D，M两点，
∴可得：D（3，2），M（1，0），
∵反比例函数经过点D，
∴k＝3×2＝6，
∴反比例函数的表达式为，令y＝3，
解得：x＝2，
∴点N的坐标为（2，3），
∴MN＝＝，
∵点P在直线DM上，
设点P的坐标为（m，m﹣1），
∴CP＝，
解得：m＝1或3，
∴点P的坐标为（1，0）或（3，2）．
故答案为：（1，0）或（3，2）．
三、解答题（本题4个小题，每小题6分，共24分）
18．参考答案：解：原式＝
＝0，
故答案为：0．
19．参考答案：解：原式＝
＝x+3，
将x＝﹣4代入得：原式＝﹣4+3＝﹣1．
20．参考答案：解：如图，过C作CD⊥AB于D，
∴∠ACD＝α，∠BCD＝β，
∴tan∠ACD＝tanα＝，tan∠BCD＝tanβ＝，
∴AD＝CD•tanα，BD＝CD•tanβ，
由AD+BD＝AB，得CD•tanα+CD•tanβ＝AB＝100，
则CD＝＞30，
∴高速公路不会受到地震影响．
21．参考答案：解：（1）摸出小球上的数字是无理数的概率＝；
（2）画树状图如下：
可知：共有9种等可能的结果，其中两个数字的乘积为有理数的有3种，
∴两次摸出的小球所标数字乘积是有理数的概率为＝．
四、（本题7分）
22．参考答案：解：∵四边形ABCD为正方形，
∴OD＝OC，∠ODF＝∠OCE＝45°，∠COD＝90°，
∵∠EOF＝90°，即∠COE+∠COF＝90°，
∴∠COE＝∠DOF，
∴△COE≌△DOF（ASA），
∴CE＝DF．
五、（本题7分）
23．参考答案：解：（1）本次接受调查的初中学生有：4÷10%＝40（人），
m%＝10÷40×100%＝25%，
n＝40×37.5%＝15，
故答案为：40，25，15；
（2）由条形统计图可得，
众数是7h，
×（5×4+6×8+7×15+8×10+9×3）＝7，
s2＝[（5﹣7）2×4+（6﹣7）2×8+（7﹣7）2×15+（8﹣7）2×10+（9﹣7）2×3]＝1.15，
故答案为：7h，1.15；
（3）1600×＝1080（人），
即该校初中学生每天睡眠时间不足8小时的有1080人．
六、（本题8分）
24．参考答案：解：（1）连接OE．
∵直线l与⊙O相切于E，
∴OE⊥l，
∵l∥BC，
∴OE⊥BC，
∴，
∴∠BAE＝∠CAE．
∴AE平分∠BAC；
（2）如图，∵AE平分∠BAC，
∴∠1＝∠4，
∵∠1＝∠5，
∴∠4＝∠5，
∵BF平分∠ABC，
∴∠2＝∠3，
∵∠6＝∠3+∠4＝∠2+∠5，即∠6＝∠EBF，
∴EB＝EF，
∵DE＝3，DF＝2，
∴BE＝EF＝DE+DF＝5，
∵∠5＝∠4，∠BED＝∠AEB，
∴△EBD∽△EAB，
∴，即，
∴AE＝，
∴AF＝AE﹣EF＝．
七、（本题10分）
25．参考答案：解：（1）由题意得：
y＝500﹣10（x﹣50）＝1000﹣10x，
w＝（x﹣40）（1000﹣10x）＝﹣10x2+1400x﹣40000；
（2）由题意得：﹣10x2+1400x﹣40000＝8000，
解得：x1＝60，x2＝80，
当x＝60时，成本＝40×[500﹣10（60﹣50）]＝16000＞10000不符合要求，舍去，
当x＝80时，成本＝40×[500﹣10（80﹣50）]＝8000＜10000符合要求，
∴销售价应定为每件80元；
（3）w＝﹣10x2+1400x﹣40000，
当x＝70时，w取最大值9000，
故销售价定为每件70元时会获得最大利润9000元．
八、（本题13分）
26．参考答案：解：（1）∵抛物线经过A（﹣1，0），B（4，0），可得：
，
解得：，
∴抛物线的解析式为：，
令x＝0，则y＝2，
∴点C的坐标为（0，2）；
（2）连接OQ，
∵点Q的横坐标为m，
∴Q（m，），
∴S＝S△OCQ+S△OBQ﹣S△OBC
＝﹣
＝﹣m2+4m，
令S＝2，
解得：m＝或，
（3）如图，过点Q作QH⊥BC于H，
∵AC＝，BC＝，AB＝5，
满足AC2+BC2＝AB2，
∴∠ACB＝90°，又∠QHP＝90°，∠APC＝∠QPH，
∴△APC∽△QPH，
∴，
∵S△BCQ＝BC•QH＝QH，
∴QH＝，
∴＝，
∴当m＝2时，存在最大值．