''2022-2023学年人教版数学八年级上册期末知识点复习课件

这是一份''2022-2023学年人教版数学八年级上册期末知识点复习课件，共60页。PPT课件主要包含了三角形定义，三角形的元素，三角形的分类，三角形三边关系，三角形的稳定性，习题训练，三角形外角的性质，多边形定义，多边形的对角线定义，正多边形定义等内容，欢迎下载使用。

第十一章 三角形
11.1与三角形有关的线段
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
边：AB，BC，CA 或 c，a，b．顶点：点 A，B，C ．内角：∠A ，∠B ，∠C．
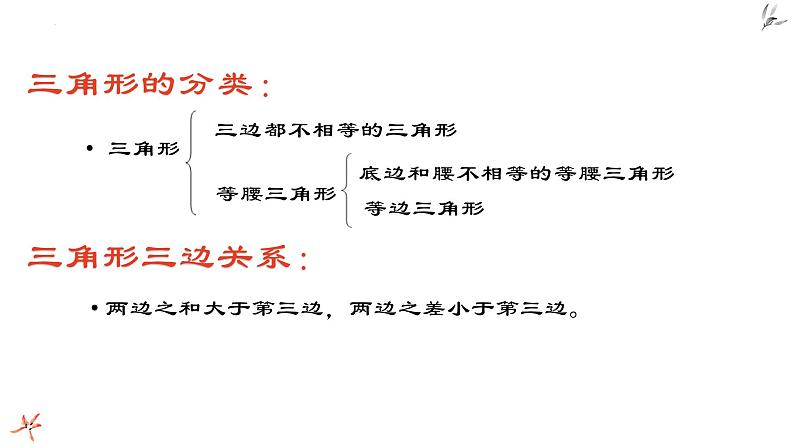
两边之和大于第三边，两边之差小于第三边。
底边和腰不相等的等腰三角形
三角形高、中线和角平分线的定义
高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高。 中线：在三角形中，连接一个顶点和它的对边中点的线段叫做三角形的中线。（三角形三条中线的交点叫做三角形的重心） 角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。
三角形的形状是固定的，三角形的这个性质叫三角形的稳定性
1.下列说法：①等边三角形是等腰三角形；②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形；③三角形的两边之差大于第三边；④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有（ ） A.1个 B.2个 C.3个 D.4个
2. 下列长度的三条线段，能组成三角形的是(　　)A．4cm，5cm，9cm B．8cm，8cm，15cmC．5cm，5cm，10cm D．6cm，7cm，14cm
3.等腰三角形的周长为20厘米.(1)若已知腰长是底长的2倍，求各边的长；(2)若已知一边长为6厘米，求其它两边的长.
解：（1）设底边长为x厘米，则腰长为2x厘米.x+2x+2x=20解得x=4.所以三边长分别为4cm,8cm,8cm.
（2）如果6厘米长的边为底边，设腰长为xcm，则6+2x=20，解得x=7；如果6厘米长的边为腰，设底边长为xcm，则2×6+x=20，解得x=8.
由以上讨论可知，其他两边的长分别为7cm，7cm或6cm，8cm.
4.下列说法正确的是(　　)A．三角形三条高都在三角形内 B．三角形三条中线相交于一点C．三角形的三条角平分线可能在三角形内，也可能在三角形外D．三角形的角平分线是射线
5. (1)如图①，AD，BE，CF是△ABC的三条中线，则AB= 2( )，BD= ( )，AE=( ).(2)如图②，AD，BE，CF是△ABC的三条角平分线，则∠1=( )， ∠3=( )， ∠ACB=2( ).
6.下列图中具有稳定性有（ ）
A.1个 B.2个 C.3个 D.4个
（注：多边形分割后有三角形也具有稳定性)
7.在建筑工地我们常可看见如图所示用木条EF、FG固定的矩形门框ABCD.这种做法根据 ( )A.两点之间线段最短B.两点确定一条直线C.三角形的稳定性D.垂线段最短
11.2与三角形有关的角
三角形的内角和定理：
三角形的内角和为180°
直角三角形内角性质和定理：
直角三角形的两个锐角互余 有两个角互余的三角形是直角三角形
性质1：三角形的一个外角等于和它不相邻的两个内角的和。 性质2：三角形的一个外角大于任何一个和它不相邻的内角。
1.求出下列各图中的x°值．
解：40°+70°+x°=180° x°=180°- 40°-70° x°=70°
解：x°+x°+x°=180° 3x°=180° x°=60°
2.如图，在△ABC中，∠B=42°，∠C=78°，AD平分∠BAC． 求∠ADC的度数.
解：∵∠B=42°，∠C=78°， ∴∠BAC=180°–∠B –∠C=60°. ∵AD平分∠BAC， ∴∠CAD= ∠BAD=30°， ∴在 △ADC中， ∴∠ADC=180°–∠C–∠CAD=72°.
3.在一个直角三角形中，有一个锐角等于40°，则另 一个锐角的度数是（　　） A．40° B．50° C．60° D．70°4.在△ABC中，若∠A=43°，∠B=47°，则这个三角形是( )
11.3多边形及内角和
在平面内，由一些线段首尾顺次相接组成的图形叫做多边形。
连接多边形不相邻的两个顶点的线段，叫做多边形的对角线。
在平面内，各个角都相等，各条边都相等的多边形叫做正多边形。
多边形相邻两边组成的角叫做它的内角。
多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
（n-2）·180° （n表示多边形的边数）
多边形的外角和为360°
n多边形对角线的条数：
从n边形的一个顶点可以引（n-3）条对角线，把多边形分成（n-2）个三角形。
n边形共有 条对角线。
1.若从一个多边形的一个顶点出发，最多可以引10条对角线，则这是 （ ）
2.过八边形的一个顶点画对角线，可以引出（ ）条对角线，把这个八边形分割成（ ）个三角形.
3. 一个多边形的内角和比四边形的内角和多720°，并且这个多边形的各内角都相等，这个多边形的每个内角是多少度？
解：设这个多边形边数为n，则 （n–2）•180=360+720，解得n=8， ∵这个多边形的每个内角都相等， （8–2）×180°=1080°， ∴它每一个内角的度数为1080°÷8=135°
12.1 全等三角形
能够完全重合的两个图形叫做全等形（形状、大小完全相同）
能够完全重合的两个三角形叫做全等三角形。
全等三角形的对应顶点、对应边、对应角：
把两个全等的三角形重合到一起，重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角。
全等三角形的对应边相等，全等三角形的对应角相等。
记两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上.
“全等”用符号“≌”表示，读作“全等于”.
∵△ABC≌△FDE，
∴A B=F D，A C=F E，B C=D E，（全等三角形对应边相等）
∠A=∠F，∠B=∠D，∠C=∠E. （全等三角形对应角相等）
全等三角形的性质的几何语言
1.能够 的两个图形叫做全等形.两个三角形 重合时，互相 的顶点叫做对应顶点.记两个全等三角形时，通常把表示 的字母写在 的位置上.
2.如图，△ABC≌ △ADE，若∠D=∠B， ∠C= ∠AED，则∠DAE= ； ∠DAB= .
3.如图，△ABC≌△BAD，如果AB=5cm， BD=4cm，AD=6cm，那么BC的长是( ) A.6cm B.5cm C.4cm D.无法确定4.在上题中，∠CAB的对应角是(　 )A.∠DAB　 B.∠DBA C.∠DBC D.∠CAD
5.如图，已知△ABD≌△ACE，∠C=45°， AC = 8， AE = 5，则∠B = ， DC = .
12.2 三角形全等的判定
（1）三边分别相等的两个三角形全等（简写为“边边边”或“SSS”）（2）两边和它们的夹角分别相等的两个三角形全等（简写为“边角边”或“SAS”）（3）两角和它们的夹边分别相等的两个三角形全等（简写为“角边角”或“ASA”）（4）两角分别相等且其中一组等角的对边相等的两个三角形全等（简写为“角角边”或“AAS”）（5）斜边和一条直角边分别相等的两个直角三角形全等（简写为“斜边、直角边”或“HL”）
证明两三角形全等或利用它证明线段或角的相等的基本方法步骤：
①确定已知条件（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形、等所隐含的边角关系）②回顾三角形判定，搞清我们还需要什么③正确地书写证明格式
1.如图，已知AB＝DF，∠B＝∠F，BE＝FC．求证△ABC≌△DFE．
证明：∵BE＝FC∴BC＝EF在△ABC和△DFE中 AB=DF ∠B=∠F BC=FE∴△ABC≌△DFE（SAS）
2.已知:如图,AB=DC,AC=BD.求证：①∠B=∠C;②OA=OD.
12.3 角的平分线的性质
角的平分线上的点到角的两边的距离相等。
角的内部到角的两边的距离相等的点在角的平分线上。
性质定理：角的平分线上的点到角的两边的距离相等.
∵OP 是∠AOB的平分线，
推理的理由有三个，必须写完全，不能少了任何一个.
PD⊥OA， PE⊥OB，
判定定理：角的内部到角的两边的距离相等的点在角的平分线上.
判断点是否在角平分线上.
∵ PD⊥OA，PE⊥OB，PD=PE.
∴点P 在∠AOB的平分线上.
2.△ABC中， ∠C=90°，AD平分∠CAB，且BC=8，BD=5，则点D到AB的距离是 .
1. 如图，DE⊥AB，DF⊥BG，垂足分别是E，F， DE =DF， ∠EDB= 60°，则 ∠EBF= 度，BE= .
3. 如图，某个居民小区C附近有三条两两相交的道路MN，OA，OB，拟在MN上建造一个大型超市，使得它到OA，OB的距离相等，请确定该超市的位置P.
4.如图，OP平分∠AOB，PC⊥OA，PD⊥OB，垂足分别是C，D，下列结论中错误的是(　　)A.PC＝PD B. OC＝ODC. ∠CPO＝∠DPO D. OC＝PC
(2)把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴.
(1)如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做___________,这条直线就是它的_________.
(3)轴对称图形的________,是任何一对对应点所连线段的垂直平分线.
(1)关于某直线对称的两个图形是全等图形;
(2)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的__________；
垂直平分线的性质和判定
性质：线段垂直平分线上的点与这条线段两个端点的距离______.
判定：与线段两个______距离相等的点在这条线段的垂直平分线上．
平面直角坐标系中轴对称
点（x, y）关于x轴对称的点的坐标 .
点（x, y）关于y轴对称的点的坐标为 .
(2)轴对称图形,等腰三角形的顶角平分线所在的直线是它的对称轴;
等腰三角形的性质及判定
(4)___________、底边上的中线和底边上的高互相重合,简称“三线合一”
(1)有两边相等的三角形是等腰三角形;
(2)如果一个三角形中有两个角相等,那么这两个角所对的边也相等（简写成“____________”）.
(3)两个_______相等,简称“等边对等角”;
⑴等边三角形的三边都相等;
⑵等边三角形的三个内角都相等,并且每一个角都等于________;
⑶是轴对称图形,对称轴是三条高所在的直线;
⑷任意角平分线、角对边上的中线、对边上的高互相重合,简称“三线合一”.
等边三角形的性质及判定
⑴三条边都相等的三角形是等边三角形.
⑵三个角都相等的三角形是等边三角形.
⑶有一个角是60°的___________是等边三角形.
1.过已知直线外的一点作该直线的垂线
2.作线段的垂直平分线
3.最短路径：(1)将军饮马问题；(2)造桥选址问题
练习1：在等腰三角形、圆、长方形、正方形、直角三角形中,一定是轴对称图形的有（ ）个
A. 1 B. 2 C. 3 D. 4
练习2：如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为______.
练习3：在直角坐标系中,点P(a,2)与点A(-3,m)关于y轴对称,则a、m的值分别为（ ）
A. 3,-2 B. -3,-2 C. 3,2 D. -3,2
关于坐标轴对称的点的坐标
练习4：如图：△ABC中,MN是AC的垂直平分线,CM=3cm,△ABC的周长是22cm,则△ABN的周长是 .
线段垂直平分线的性质和判定
练习5：如图, △ABC中,∠A=36 °,AB=AC, BD平分∠ABC交AC于点D,则图中的等腰三角形共有 个.
练习6：如图,已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在B1处,DB1、EB1分别交边AC于M、H点,若∠ADM=50 °,则∠EHC的度数为 .
等腰三角形的性质和判定
含30°角的直角三角形的性质
关于坐标轴对称的点的坐标
第十四章 整式乘除与因式分解
14.1 一、幂的有关运算
14.1.1 同底数幂相乘
（m、n为正整数）注amanap=am+n+p
14.1.2 幂的乘方
1．下列算式中，结果等于a6的是（　　）A．a4+a2 B．a2+a2+a2C．a2•a3 D．a2•a2•a2
【解析】∵a4+a2≠a6，∴选项A的结果不等于a6；∵a2+a2+a2=3a2，∴选项B的结果不等于a6；∵a2•a3=a5，∴选项C的结果不等于a6；∵a2•a2•a2=a6，∴选项D的结果等于a6。
2．下面的计算不正确的是（　　）A．5a3-a3=4a3 B．2m•3n=6m+nC．2m•2n=2m+nD．-a2•（-a3）=a5
【解析】A、5a3-a3=（5-1）a3=4a3，正确；B、2m与3n与底数不相同，不能进行运算，故本选项错误；C、2m•2n=2m+n，正确；D、-a2•（-a3）=a2+3=a5，正确。故选B。
3．若m=2125，n=375，则m、n的大小关系正确的是（　）A．m＞nB．m＜nC．m=n D．大小关系无法确定
【解析】∵m=2125=（25）25=3225，n=375=（33）25=2725，∴m＞n，故选A。
4．设2m=8，2n=16，则2m+3n等于（　　）A．12B．18C．45D．64
【解析】∵2m=8，2n=16，∴m=3 n=4则2m+3n=18
14.1.4整式的乘法和除法
单位 拜什艾日克镇中学教师 杨涛
（1）、单项式乘以单项式
14.1.4整式的乘法
单项式与单项式相乘，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。
（2）、单项式乘以多项式p（a+b+c）=pa+pb+pc（3）、多项式乘以多项式(a+b)(p+q)= (ap+aq+bp+bq)
14.1.4整式的乘法
同底数幂相除，底数不变，指数相减，
14.1.4整式的除法
（1）．单项式除以单项式法则：把系数、同底数幂别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式。（2）．多项式除以单项式的法则：先把这个多项式的每一项除以这个单项式，再把所得的商相加。（3）．零指数幂的概念：任何一个不等于零的数的零指数幂都等于1，
1．已知将（x3+mx+n）（x2-3x+4）乘开的结果不含x2项，并且x3的系数为2。求m、n的值；
【答案】原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n=x5-3x4+（4+m）x3+（-3m+n）x2+（4m-3n）x+4n．∵不含x2项，并且x3的系数为2，∴4+m=2，-3m+n=0，解得m=-2，n=-6；
2．设M=（x-3）（x-7），N=（x-2）（x-8），则M与N的关系为什么？
【解析】M=（x-3）（x-7）=x2-10x+21，N=（x-2）（x-8）=x2-10x+16，M-N=（x2-10x+21）-（x2-10x+16）=5，则M＞N。
3．已知52x+1÷5x-1=25x-3，求x的值。
【答案】由幂的乘方，得：52x+1÷5x-1=52x-6，由同底数幂的除法法则，得：52x+1-（x-1）=52x-6，∴2x+1-（x-1）=2x-6。解得：x=8。
4.如果9m+3×27m+1÷32m-1=81，求m的值。
【答案】∵9m+3×27m+1÷32m-1=81，∴（32）m+3×（33）m+1÷32m-1=34，∴32m+6×33m+3÷32m-1=34，∴33m+10=34，∴3m+10=4，解得，m=-2，即m的值是-2。
14.2平方差公式和完全平方公式
两个数的和与这两个数的差相乘，等于这两个数的平方差，即；
14.2.1平方差公式
两数和（或差）的平方等于它们的平方和，加（或减）它们的积的2倍，即
14.2.2完全平方公式
1.化简：（3b-a-2c）（2c-3b-a）
【答案】（3b-a-2c）（2c-3b-a）=[-a+（3b-2c）][-a-（3b-2c）]=a2-（3b-2c）2=a2-9b2+12bc-4c2
2．如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，则中间空白部分的面积是（　）
A．abB．（a+b）2C．（a-b）2D．a2-b2
由题意可得，正方形的边长为（a+b），故正方形的面积为（a+b）2，又∵原矩形的面积为4ab，∴中间空的部分的面积=（a+b）2-4ab=（a-b）2。
因式分解概念分解对象是多项式，分解结果必需是积的形式，且积的因式必需是整式；因式分解必需是恒等变形；因式分解必需分解到每一个因式都不能分解为止。因式分解与整式乘法是互逆变形，因式分解是把和差化为积的形式，而整式乘法是把积化为和差的形式。
14.3.1提公因式法因式分解：
提公因式法的步骤：第一步是找出公因式；第二步是提取公因式并肯定另一因式．需注意的是，提取完公因式后，另一个因式的项数与原多项式的项数一致，这一点可用来查验是不是漏项．注意点：A提取公因式后各因式应该是最简形式，即分解到“底”；B若是多项式的第一项的系数是负的，一般要提出“－”号，使括号内的第一项的系数是正的。
14.3.1提公因式法因式分解：
提因式分解(1)3x3＋6x4； (2)4a3b2－10ab3c；
解：(1)原式＝3x3(1＋2x).　 (2)原式＝2ab2(2a2－5bc).　
(1)4x2－y2; 　　　　　(2)－16＋a2b2；
解(1)原式＝(2x＋y)(2x－y).　 (2)原式＝(ab＋4)(ab－4).　
3.x2＋4x＋4＝（___________）2 .
【解析】根据完全平方公式的特征进行因式分解可得: x2＋4x＋4＝ ,故答案为x＋2.
第十五章 分式
15.1分式和分式的基本性质
分式的定义：　　一般地，如果A，B 表示两个整式，并且B 中含有字母，那么式子 叫做分式.分式 中，A 叫做分子，B 叫做分母.
当B≠0时，分式 有意义，当B=0，分式 无意义；当B≠0且A=0时，分式 的值为零.
分式的基本性质： 分式的分子与分母乘（或除以）同一个不等于0的整式，分式的值不变．
其中A，B，C是整式.
根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分式的约分．分子与分母没有公因式的式子，叫做最简分式．根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分.
2.当x取何值时，分式 有意义？x 取何值时，分式的值为0？
注意：分式的约分，一般要约去分子和分母所有的公因式，使所得结果成为最简分式或者整式.
　　解：（1）最简公分母是
分式的乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母.
分式的除法法则： 　分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘.
分式乘除混合运算：乘除混合运算可以统一为乘法运算.
分式的乘方法则：分式乘方要把分子、分母分别乘方．
数与式有相同的混合运算顺序：先乘方，再乘除.
分式的加减法法则： 同分母分式相加减，分母不变，把分子相加减；异分母分式相加减，先通分，变为同分母的分式，再加减．
分式加减乘除混合运算：
数与式有相同的混合运算顺序：先乘方，再乘除，最后加减.
负整数指数的意义：n是正整数时,
对于一个小于1的正小数，从小数点前的第一个0算起至小数点后第一个非0数字前有几个0，用科学记数法表示这个数时，10的指数就是负几．
乘除混合运算可以统一为乘法运算.
6. 斑叶兰被列为国家二级保护植物,它的一粒种子重约0.000 000 5克将0. 000 000 5用科学记数法表示(  ) A.5×107 B.5×10-7 C.0.5×10-6 D.5×10-6
负指数幂的科学记数法：
像这样分母中含未知数的方程叫做分式方程。解分式方程时要进行检验。
解分式方程①的基本思路：是将分式方程化为整式方程，具体做法是“去分母” 即方程两边同乘最简公分母.这也是解分式方程的一般方法.
增根: 在去分母,将分式方程转化为整式方程的过程中出 现的不适合于原方程的根.
温馨提示:使最简公分母的值为零的解叫做增根. 注意：增根是去分母后整式方程的解,不是原分式方程的解.
检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则,这个解不是原分式方程的解。
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.2.设:选择恰当的未知数,注意单位和语言完整.3.列:根据数量和相等关系,正确列出方程.4.解:认真仔细解这个分式方程.5.验:检验.6.答:注意单位和语言完整.
解：方程两边都乘以 x ( x – 2 ) , 约去分母，得
5 ( x – 2 ) = 7x
检验：当 x = – 5 时，
x ( x – 2 ) = (– 5)(– 5 – 2) = 35 ≠0
所以x= – 5 是原方程的根.
2. 解分式方程
解 : 方程两边同乘以(x －1)(x ＋2),得
x(x＋2)－(x－1)(x＋2)＝3
化简,得 x＋2 ＝ 3
解得 x＝1
检验:当x ＝ 1 时，(x＋2)(x－1)=0，
x ＝1不是原方程的根.
∴ 原分式方程无解 .