第10讲　磁场（含解析）--2024年高考物理大二轮复习讲义

这是一份第10讲　磁场（含解析）--2024年高考物理大二轮复习讲义，共13页。
1.会用安培定则判断磁场的方向，会进行磁感应强度的叠加。
2会分析和计算安培力、洛伦兹力的方向和大小。
3会判断带电粒子在磁场中的运动性质并会解决相应问题。
考点一 磁场的基本性质 安培力
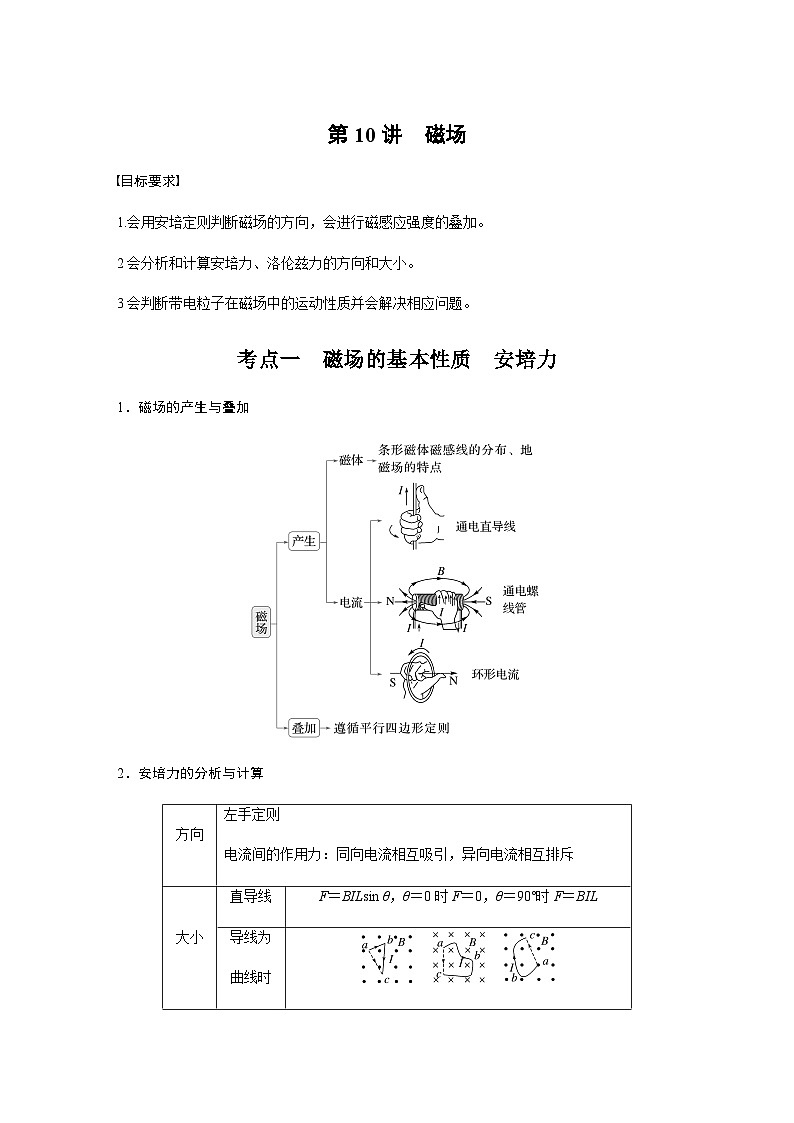
1．磁场的产生与叠加
2．安培力的分析与计算
例1 如图所示，M、N和P是以MN为直径的半圆弧上的三点，O为半圆弧的圆心，∠MOP＝60°，在M、N处各有一长直导线垂直穿过纸面，电流方向如图所示，且IM＝2IN(已知电流为I的长直导线在其周围激发的磁场中，距导线距离为r处的磁感应强度大小为B＝keq \f(I,r)，其中k为常数)，此时O点的磁感应强度大小为B1。若将M处长直导线移至P处，则此时O点的磁感应强度( )
A．大小为eq \r(3)B1，方向水平向右
B．大小为eq \r(3)B1，方向水平向左
C．大小为2B1，方向与水平方向夹角为30°斜向右下
D．大小为2B1，方向与水平方向夹角为30°斜向右上
学习笔记：______________________________________________________________
________________________________________________________________________
例2 如图所示，半径为R的金属圆环用绝缘轻质细线悬挂于天花板上，金属圆环中通以逆时针方向的电流，图中A、C与圆心O连线的夹角为120°，只在直线AC上方区域内加一垂直于纸面向里的匀强磁场，磁感应强度大小为B，金属圆环处于静止状态时，细线中的拉力大小为F1；若只在直线AC下方区域内加与上述相同的磁场，金属圆环处于静止状态时，细线中的拉力大小为F2，则金属圆环中的电流大小为( )
A.eq \f(\r(3)F1－F2,6BR) B.eq \f(\r(3)F1－F2,3BR)
C.eq \f(3F1－F2,4πBR) D.eq \f(3F1－F2,2πBR)
学习笔记：______________________________________________________________
________________________________________________________________________
考点二 带电粒子在匀强磁场中的运动
1．分析带电粒子在匀强磁场中运动的方法
2.带电粒子在有界匀强磁场中运动的三个重要结论
(1)粒子从同一直线边界射入磁场和射出磁场时，入射角等于出射角(如图甲，θ1＝θ2＝θ3)。
(2)沿半径方向射入圆形磁场的粒子，出射时亦沿半径方向(如图乙，两侧关于两圆心连线对称)。
(3)粒子速度方向的偏转角等于其轨迹的对应圆心角(如图甲，α1＝α2)。
3．带电粒子在磁场中运动的多解成因
(1)磁场方向不确定形成多解；
(2)带电粒子电性不确定形成多解；
(3)速度不确定形成多解；
(4)运动的周期性形成多解。
例3 (2023·全国乙卷·18)如图，一磁感应强度大小为B的匀强磁场，方向垂直于纸面(xOy平面)向里，磁场右边界与x轴垂直。一带电粒子由O点沿x正向入射到磁场中，在磁场另一侧的S点射出，粒子离开磁场后，沿直线运动打在垂直于x轴的接收屏上的P点；SP＝l，S与屏的距离为eq \f(l,2)，与x轴的距离为a。如果保持所有条件不变，在磁场区域再加上电场强度大小为E的匀强电场，该粒子入射后则会沿x轴到达接收屏。该粒子的比荷为( )
A.eq \f(E,2aB2) B.eq \f(E,aB2) C.eq \f(B,2aE2) D.eq \f(B,aE2)
学习笔记：______________________________________________________________
________________________________________________________________________
例4 (2023·江苏南京市模拟)a、b两个带正电的粒子经同一电场由静止加速，先后以v1、v2从M点沿MN进入矩形匀强磁场区域，经磁场偏转后分别从PQ边E、F离开。直线ME、MF与MQ的夹角分别为30°、60°，粒子的重力不计，则两个粒子进入磁场运动的速度大小之比为( )
A．v1∶v2＝1∶3 B．v1∶v2＝3∶1
C．v1∶v2＝3∶2 D．v1∶v2＝2∶3
学习笔记：______________________________________________________________
________________________________________________________________________
例5 (2023·江苏扬州市期末)云室中存在磁感应强度大小为B的匀强磁场，一个质量为m、速度为v的电中性粒子在A点分裂成带等量异种电荷的粒子a和b，如图所示，a、b在磁场中的径迹是两条相切的圆弧，半径之比ra∶rb＝6∶1，相同时间内的径迹长度之比la∶lb＝3∶1，不计重力及粒子间的相互作用力，则( )
A．粒子a电性为正
B．粒子a、b的质量之比ma∶mb＝6∶1
C．粒子a、b在磁场中做圆周运动的周期之比Ta∶Tb＝1∶2
D．粒子b的动量大小pb＝eq \f(1,7)mv
学习笔记：______________________________________________________________
________________________________________________________________________
考点三 带电粒子在有界匀强磁场中运动的临界与极值问题
1．解决带电粒子在匀强磁场中运动的临界问题，关键在于运用动态思维，利用动态圆思想寻找临界点，确定临界状态，根据粒子的速度方向找出半径方向，同时由磁场边界和题设条件画好轨迹，定好圆心，建立几何关系。
2．粒子射出或不射出磁场的临界状态是粒子运动轨迹与磁场边界相切。
3.常见的动态圆
例6 如图所示，S为一离子源，MN为足够长的荧光屏，S到MN的距离为SP＝L，MN左侧区域有足够大的匀强磁场，磁感应强度大小为B，方向垂直纸面向里。某时刻离子源S一次性沿平行纸面各个方向均匀地喷发大量的质量为m、电荷量为q、速率为eq \f(qBL,m)的正离子(此后不再喷发)，不计离子重力，不考虑离子之间的相互作用力。则( )
A．打中荧光屏的最短时间为eq \f(πm,3qB)
B．打中荧光屏的最长时间为eq \f(πm,qB)
C．打中荧光屏的宽度为2eq \r(3)L
D．打到荧光屏的离子数与发射的总离子数比值为eq \f(1,3)
学习笔记：______________________________________________________________
________________________________________________________________________
例7 如图所示，半径为R的圆形区域的圆心位于直角坐标系的坐标原点O，该圆形区域内有垂直坐标平面的匀强磁场(图中未画出)。磁场区域外右侧有宽度为R的粒子源，M、N为粒子源两端点，M、N连线垂直于x轴，粒子源中点P位于x轴上，粒子源持续向x轴负方向发射质量为m、电荷量为q(q>0)、速率为v的粒子。已知从粒子源中点P发出的粒子，经过磁场区域后，恰能从圆与y轴负半轴的交点Q处沿y轴负方向射出磁场，不计粒子重力及粒子间相互作用力。求：
(1)匀强磁场的磁感应强度；
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(2)从粒子源发出的粒子经过磁场区域的路程范围。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
1.(2023·江苏省学业水平考试模拟)已知通电直导线在其延长线上产生的磁感应强度大小为零，通电圆形导线在其圆心处产生的磁感应强度大小与电流大小成正比，与圆形导线的半径成反比，即B＝keq \f(I,r)，k为比例系数。现有两段四分之一圆弧导线和两段直导线组成的闭合回路如图所示，O为两段圆弧的共同圆心，大、小圆弧的半径分别为r大和r小，回路中通有电流I，则圆心O处磁感应强度的大小和方向分别为( )
A．kI(eq \f(1,r小)－eq \f(1,r大))，垂直纸面向外
B．kI(eq \f(1,r小)＋eq \f(1,r大))，垂直纸面向里
C.eq \f(kI,4)(eq \f(1,r小)－eq \f(1,r大))，垂直纸面向外
D.eq \f(kI,4)(eq \f(1,r小)＋eq \f(1,r大))，垂直纸面向里
2.如图所示，边长为eq \r(3)L的正三角形abc区域内存在方向垂直纸面向外的匀强磁场(图中未画出)，正三角形中心O有一粒子源，可以沿abc平面任意方向发射相同的带电粒子，粒子质量为m，电荷量为q。粒子速度大小为v时，恰好没有粒子穿出磁场区域，不计粒子的重力及粒子间相互作用力。下列说法正确的是( )
A．磁感应强度大小为eq \f(2mv,qL)
B．磁感应强度大小为eq \f(4mv,qL)
C．若发射粒子速度为2v时，在磁场中运动的最短时间为eq \f(2πL,3v)
D．若发射粒子速度为2v时，在磁场中运动的最短时间为eq \f(πL,6v)
第10讲 磁场
例1 A [设N处导线在O点激发磁场的磁感应强度大小为B0，则M处导线在O点激发的磁场的磁感应强度大小为2B0，M处导线未移动时，各导线在O点激发磁场的磁感应强度如图中实线所示，可得B1＝B0，将M处导线移到P处时，在O点激发磁场的磁感应强度大小仍为2B0，如图中虚线所示，N处导线在O点激发磁场的磁感应强度不变，则此时合磁感应强度大小为eq \r(3)B0，即eq \r(3)B1，方向水平向右，故A正确。]
例2 A [通电圆环在磁场中的有效长度均为L＝2Rsin 60°＝eq \r(3)R，只在直线AC上方区域内加一垂直于纸面向里的匀强磁场，根据左手定则可知安培力的方向向下，细线中的拉力大小为F1＝mg＋BI·eq \r(3)R，若只在直线AC下方区域加与上述相同的磁场，根据左手定则可得安培力的方向向上，则F2＝mg－BI·eq \r(3)R，联立解得I＝eq \f(\r(3)F1－F2,6BR)，故选A。]
例3 A [由题知，带电粒子由O点沿x轴正方向入射到磁场中，在磁场另一侧的S点射出，则根据几何关系可知粒子做圆周运动的半径r＝2a，粒子做圆周运动有qvB＝meq \f(v2,r)，则eq \f(q,m)＝eq \f(v,2aB)，如果保持所有条件不变，在磁场区域再加上电场强度大小为E的匀强电场，该粒子入射后则会沿x轴到达接收屏，有Eq＝qvB，联立有eq \f(q,m)＝eq \f(E,2aB2)，故选A。]
例4 B [a、b两个带正电的粒子在磁场中的运动轨迹如图
设a粒子的轨迹半径为R1，b粒子的轨迹半径为R2，MQ＝d，由几何关系得
R1＋R1sin 30°＝d，R2－R2sin 30°＝d
解得R1∶R2＝1∶3
设加速电场的电压为U，匀强磁场的磁感应强度为B，有
Uq＝eq \f(1,2)mv2，qvB＝meq \f(v2,R)
可得v＝eq \f(2U,BR)
则v1∶v2＝3∶1，故选B。]
例5 D [由题图中轨迹结合左手定则可知，粒子a电性为负，故A错误；相同时间内的径迹长度之比la∶lb＝3∶1，可知粒子a、b的速率之比为va∶vb＝la∶lb＝3∶1，根据洛伦兹力提供向心力有qvB＝meq \f(v2,r)，可得r＝eq \f(mv,qB)，由于粒子a、b的电荷量大小相等，半径之比ra∶rb＝6∶1，则有mava∶mbvb＝ra∶rb＝6∶1，联立可得ma∶mb＝2∶1，故B错误；根据周期表达式T＝eq \f(2πm,qB)可得粒子a、b在磁场中做圆周运动的周期之比Ta∶Tb＝ma∶mb＝2∶1，故C错误；根据动量守恒可得mv＝mava＋mbvb，又mava∶mbvb＝6∶1，联立可得粒子b的动量大小为pb＝mbvb＝eq \f(1,7)mv，故D正确。]
例6 A [根据qvB＝meq \f(v2,r)，则离子轨迹半径r＝eq \f(mv,qB)＝L，离子轨迹对应弦长最短时运动时间最短，即离子恰好打中P点，如图甲所示
根据几何关系可知，轨迹对应的圆心角为60°，能打中荧光屏的最短时间为t＝eq \f(1,6)T＝eq \f(πm,3qB)，故A正确；
离子运动轨迹如图乙所示
离子速度为v1时从下侧回旋，刚好和边界相切于B点，离子速度为v2时从上侧回旋，刚好和上边界相切于A点，打到B点的离子离开S时的初速度方向和打到A点的离子离开S时的初速度方向夹角θ＝π，能打到荧光屏上的离子数与发射的离子总数之比k＝eq \f(θ,2π)＝eq \f(1,2)，离子的周期T＝eq \f(2πm,qB)，打中荧光屏的最长时间为t＝eq \f(270°,360°)T＝eq \f(3πm,2qB)，故B、D错误；
离子打中荧光屏的范围总长度为图乙中的AC长度，由几何关系可知|AC|＝(eq \r(3)＋1)R＝(eq \r(3)＋1)L，打中荧光屏的宽度为(eq \r(3)＋1)L，故C错误。]
例7 (1)eq \f(mv,qR)，方向垂直纸面向里
(2)eq \f(πR,3)≤s≤eq \f(2πR,3)
解析 (1)根据题意可知从粒子源中点P发出的粒子在磁场里运动轨迹为四分之一圆周，轨迹半径为r1，由几何关系可知r1＝R
根据洛伦兹力提供向心力，有qvB＝meq \f(v2,r1)
联立解得B＝eq \f(mv,qR)
根据左手定则可知，磁感应强度方向垂直纸面向里。
(2)根据题意可知，从N点出射的粒子在磁场中运动的路程最短，如图甲所示
根据几何关系可得cs∠COB＝eq \f(\f(R,2),R)＝eq \f(1,2)
解得∠COB＝60°
因为四边形OBO1Q为菱形，
所以∠QO1B＝60°
则粒子经过磁场区域的最短路程为
s1＝eq \f(1,6)×2πR＝eq \f(πR,3)
根据题意可知，从M点出射的粒子在磁场中运动的路程最长，如图乙所示
易知四边形O2DOQ为菱形，根据几何关系可知∠QO2D＝120°
则粒子经过磁场区域的最长路程为
s2＝eq \f(1,3)×2πR＝eq \f(2πR,3)
所以从粒子源发出的粒子经过磁场区域的路程范围为eq \f(πR,3)≤s≤eq \f(2πR,3)。
高考预测
1．C [由电流方向及安培定则可知，大、小圆弧导线在圆心O处产生的磁场方向相反，分别为垂直纸面向里、垂直纸面向外，由题可知，小圆弧导线产生的磁场的磁感应强度大于大圆弧导线产生的，故圆心处磁感应强度的方向垂直纸面向外，B、D错误；题中大、小圆弧均为四分之一圆弧，故圆心处磁感应强度的大小为eq \f(kI,4)(eq \f(1,r小)－eq \f(1,r大))，A错误，C正确。]
2．B [磁场垂直纸面向外，粒子恰好没有穿出磁场区域，因此粒子运动轨迹的直径等于过O点垂直于bc的线段大小，设垂足为d，由几何关系得Od＝eq \f(1,2)L，所以半径r＝eq \f(1,4)L，由于洛伦兹力提供向心力qvB＝meq \f(v2,r)，解得B＝eq \f(mv,qr)＝eq \f(4mv,qL)，故A错误，B正确；当发射粒子速度为2v时，由q×2vB＝meq \f(4v2,r1)，解得r1＝eq \f(2mv,Bq)＝eq \f(L,2)，粒子在磁场中运动的最短时间就是在磁场中转过最小的角度，当粒子从垂足d出去时，时间最短，由几何关系可得，转过的角度为θ＝60°，则时间为eq \f(T,6)，又因为T＝eq \f(2πm,qB)＝eq \f(2πm,\f(4mv,qL)q)＝eq \f(πL,2v)，即有t＝eq \f(T,6)＝eq \f(πL,12v)，故C、D错误。]
方向
左手定则
电流间的作用力：同向电流相互吸引，异向电流相互排斥
大小
直导线
F＝BILsin θ，θ＝0时F＝0，θ＝90°时F＝BIL
导线为
曲线时
等效为ac直线电流
受力
分析

根据力的平衡条件或牛顿运动定律列方程
基本
思路
(1)画轨迹：确定圆心，用几何方法求半径并画出轨迹
(2)找联系：轨迹半径与磁感应强度、运动速度相联系，偏转角度与圆心角、运动时间相联系，运动时间与周期相联系
(3)用规律：利用牛顿第二定律和圆周运动的规律，特别是半径公式和周期公式
基本
公式
qvB＝meq \f(v2,r)，T＝eq \f(2πr,v)
重要
结论
r＝eq \f(mv,qB)，T＝eq \f(2πm,qB)
圆心的
确定
(1)轨迹上的入射点和出射点的速度垂线的交点为圆心，如图(a)
(2)轨迹上入射点速度垂线和两点连线中垂线的交点为圆心，如图(b)
(3)沿半径方向距入射点距离等于r的点，如图(c)(当r已知或可算)
半径的
确定
方法一：由物理公式求，由于qvB＝eq \f(mv2,r)
所以半径r＝eq \f(mv,qB)
方法二：由几何关系求，一般由数学知识(勾股定理、三角函数等)通过计算来确定
时间的
求解
方法一：由圆心角求，t＝eq \f(θ,2π)·T
方法二：由弧长求，t＝eq \f(s,v)
示意图
适用条件
应用方法
放缩圆
(轨迹圆的圆心在P1P2直线上)
粒子的入射点位置相同，速度方向一定，速度大小不同
以入射点P为定点，将半径放缩作轨迹圆，粒子恰好不射出磁场的临界状态是粒子运动轨迹与磁场边界相切
旋转圆
(轨迹圆的圆心在以入射点P为圆心、半径R＝eq \f(mv0,qB)的圆上)
粒子的入射点位置相同，速度大小一定，速度方向不同
将一半径为R＝eq \f(mv0,qB)的圆以入射点为圆心进行旋转，从而探索出临界条件
平移圆
(轨迹圆的所有圆心在一条直线上)
粒子的入射点位置不同，速度大小、方向均一定
将半径为R＝eq \f(mv0,qB)的圆进行平移
磁聚焦与
磁发散
磁聚焦
磁发散
粒子速度大小相同，轨迹圆半径等于区域圆半径
带电粒子平行射入圆形有界匀强磁场，则粒子从磁场边界上同一点射出，该点切线与入射方向平行——磁聚焦，从边缘某点以不同方向入射时平行出射——磁发散