2023-2024学年山西省运城市盐湖区九年级（上）期中数学试卷（含解析）

这是一份2023-2024学年山西省运城市盐湖区九年级（上）期中数学试卷（含解析），共35页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1．用配方法解方程x2+4x+1＝0时，原方程应变形为（ ）
A．（x+2）2＝3B．（x﹣2）2＝3C．（x+2）2＝5D．（x﹣2）2＝5
2．已知在平行四边形ABCD中，对角线AC与BD相交于点O．添加一个条件后，平行四边形ABCD为矩形，则这个条件可以是（ ）
A．AB＝BCB．AO＝COC．AC＝BDD．AO⊥BO
3．在一个不透明的布袋中装有52个白球和若干个黑球，除颜色外其他都相同，小强每次摸出一个球记录下颜色后并放回，通过多次试验后发现，摸到黑球的频率稳定在0.2左右，则布袋中黑球的个数可能有（ ）
A．11B．13C．24D．30
4．已知，则的值为（ ）
A．B．1C．D．
5．顺次连接下列图形的各边中点，所得图形为矩形的是（ ）
①矩形；
②菱形；
③对角线相等的四边形；
④对角线互相垂直的四边形．
A．①③B．②③C．②④D．③④
6．已知实数m，现甲、乙、丙、丁四人对关于x的方程（m﹣2）x2+2x﹣1＝0讨论如下，则下列判断正确的是（ ）
A．甲和丙说得对B．甲和丁说得对
C．乙和丙说得对D．乙和丁说得对
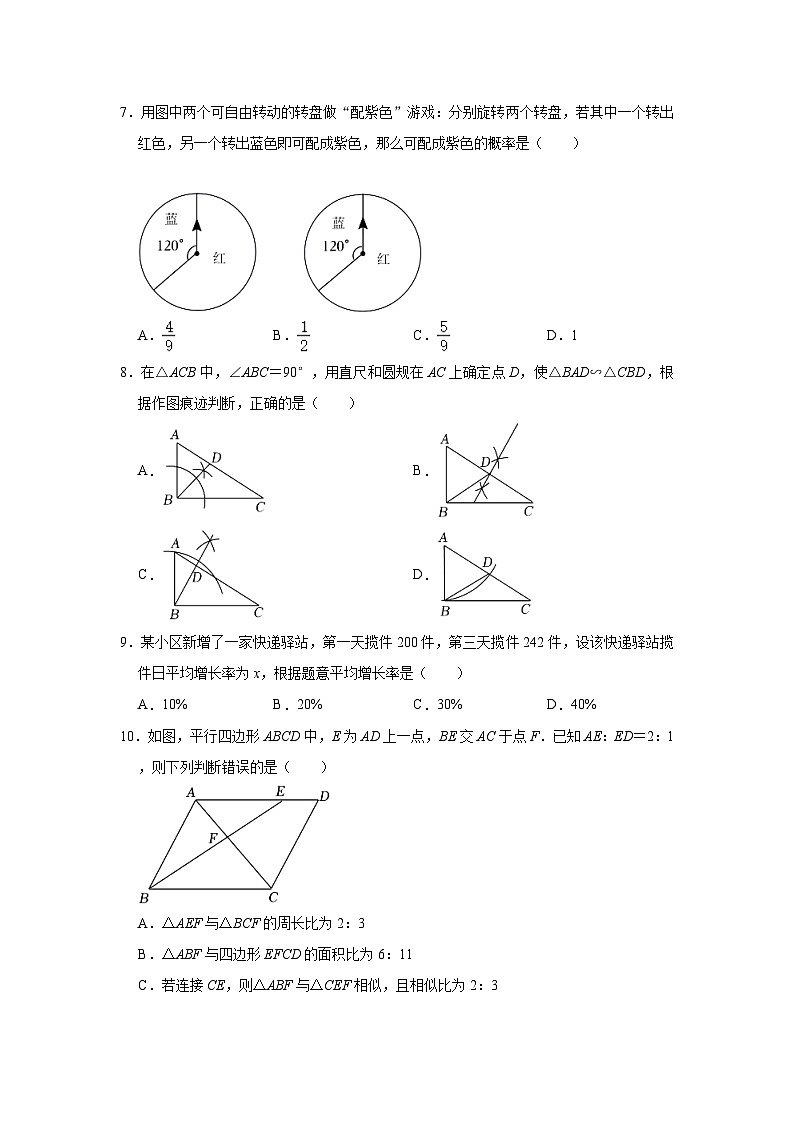
7．用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，那么可配成紫色的概率是（ ）
A．B．C．D．1
8．在△ACB中，∠ABC＝90°，用直尺和圆规在AC上确定点D，使△BAD∽△CBD，根据作图痕迹判断，正确的是（ ）
A．B．
C．D．
9．某小区新增了一家快递驿站，第一天揽件200件，第三天揽件242件，设该快递驿站揽件日平均增长率为x，根据题意平均增长率是（ ）
A．10%B．20%C．30%D．40%
10．如图，平行四边形ABCD中，E为AD上一点，BE交AC于点F．已知AE：ED＝2：1，则下列判断错误的是（ ）
A．△AEF与△BCF的周长比为2：3
B．△ABF与四边形EFCD的面积比为6：11
C．若连接CE，则△ABF与△CEF相似，且相似比为2：3
D．若题中条件“AE：ED＝2：1”改为“点E为边AD的黄金分割点，AE＞ED“，则＝
二、填空题（本大题共5小题，每小题3分，共15分）
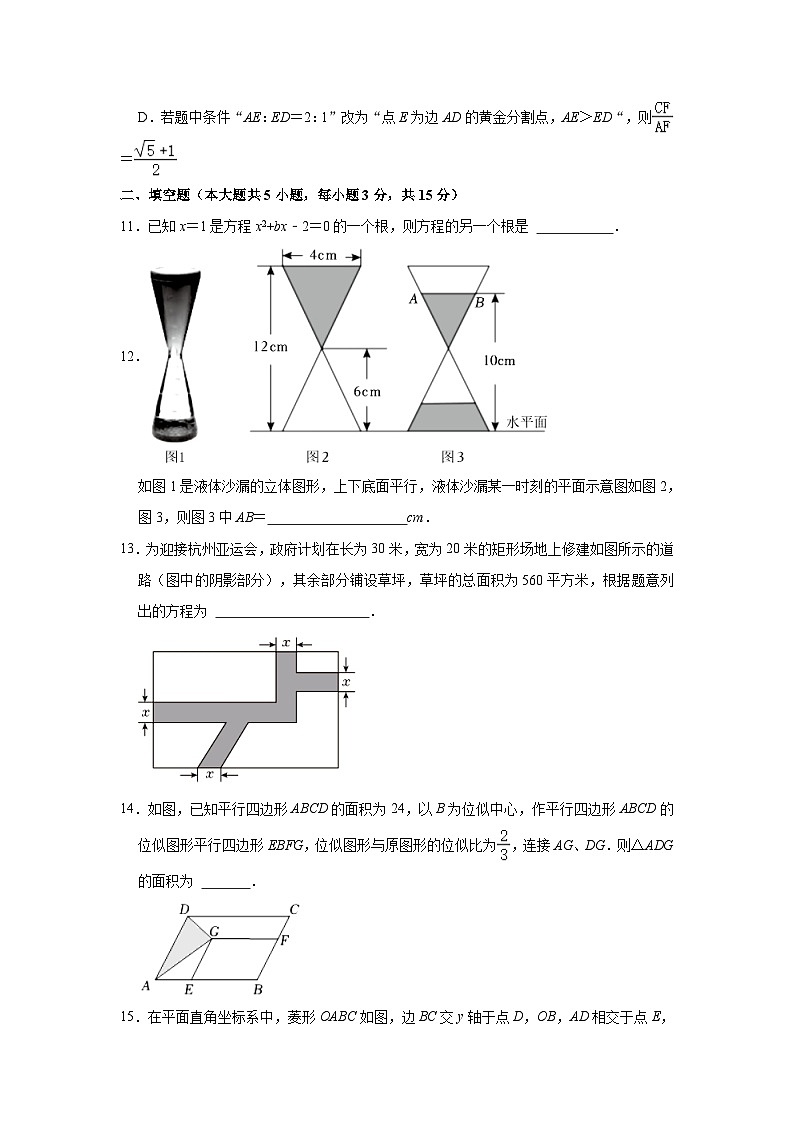
11．已知x＝1是方程x2+bx﹣2＝0的一个根，则方程的另一个根是 ．
12．
如图1是液体沙漏的立体图形，上下底面平行，液体沙漏某一时刻的平面示意图如图2，图3，则图3中AB＝ cm．
13．为迎接杭州亚运会，政府计划在长为30米，宽为20米的矩形场地上修建如图所示的道路（图中的阴影部分），其余部分铺设草坪，草坪的总面积为560平方米，根据题意列出的方程为 ．
14．如图，已知平行四边形ABCD的面积为24，以B为位似中心，作平行四边形ABCD的位似图形平行四边形EBFG，位似图形与原图形的位似比为，连接AG、DG．则△ADG的面积为 ．
15．在平面直角坐标系中，菱形OABC如图，边BC交y轴于点D，OB，AD相交于点E，点A的坐标为（6，0），∠OCB＝60°，则点E的坐标为 ．
三、解答题（本大题共8小题，共75分.解答应写出文字说明、证明过程或演算步骤）
16．（1）3x2+8x﹣3＝0；
（2）5x2+2x﹣1＝0；
（3）2（x﹣3）2＝x2﹣9．
17．一个不透明的口袋里装有分别标有汉字“杭”、“州”、“亚”、“运”、“会”的五个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
（1）若从中任取一个球，求摸出球上的汉字刚好是“运”的概率是 ；
（2）小华和小林商定了一个游戏规则：摇匀后随机摸出两个小球，若取出的两个球上恰好有汉字“运”则小林获胜；否则小华获胜．请用列表法或画树状图的方法说明这个游戏规则对双方是否公平．
18．如图，四边形ABCD中，∠ABC＝90°，AD∥BC，AD＝BC，点E是AD上一点，连接BE，CE，且∠BEC＝90°，点F是BC的中点．
（1）求证：四边形ABCD是矩形；
（2）若∠ECD＝30°，EF＝4，求矩形的面积．
19．某超市销售一种衬衫．平均每天可售出20件，每件盈利40元．为了扩大销售、增加盈利，该超市准备适当降价，经过一段时间测算，发现每件衬衫每降低1元，平均每天可多售出2件．
（1）在每件盈利不少于25元的前提下，要使该衬衫每天销售获利为1200元，问每件衬衫应降价多少元？
（2）小明的观点：“该衬衫每天的销售获利能达到1300元”，你同意小明的观点吗？若同意，请求出每件衬衫应降价多少元？若不同意，请说明理由．
20．数学思想方法作为数学学科的一般原理，在数学学习中至关重要．我们经常运用转化、类比、数形结合、从特殊到一般等思想方法来解决一些数学问题．
如图①，在平行四边形ABCD中，点E是AB边的中点，点G是线段BC上一点，AG与DE相交于点F．若，求的值．
【尝试探究】在图①中，过点E作EH∥AD交AG于点H，则的值为 ，的值为 的值为 ．
【类比延伸】如图②，在①的条件下，若，则的值为 （用含a的代数式表示）．
【拓展迁移】如图③，在平行四边形ABCD中，点E是AB边的中点，若点G在线段CB的延长线上，AG交DE的延长线于点F，若，则的值为 （用含m的代数式表示）．
21．操作与探究
【操作】在数学实践课上，老师要求同学们对如图1的△ABC纸片进行以下操作，并探究其中的问题：
第一步：如图2，沿过点B的直线折叠，使得点A落在BC上，展开铺平该纸片，折痕为BD；
第二步：如图3，继续折叠该纸片，使得点B与点D重合，展开铺平该纸片，折痕为EF；
第三步：如图4，连接DE，DF．
【探究】
任务一：判断四边形BEDF的形状，并说明理由；
任务二：在△ABC纸片中，若∠ABC＝60°，折痕EF＝2，四边形BEDF的面积为 ．
22．综合与实践
【模型探索】如图1，在正方形ABCD中，点E，F分别在边DC，BC上，若AF⊥BE，则AF与BE的数量关系为 ．
【模型应用】如图2，将边长为2的正方形ABCD折叠，使点B落在CD边的中点E处，点A落在点F处，折痕交AD于点M，交BC于点N，则线段MN的长度是 ．
【知识迁移】如图3，在矩形ABCD中，AB＝2，BC＝3，点E在边CD上，点P，Q分别在边AD，BC上，且 AE⊥PQ，则的值为 ．
【综合应用】如图4，正方形ABCD的边长为12，点F是BC上一点，将△ABF沿AF折叠，使点B落在点B'处，连接BB'并延长交CD于点E．若CE＝5，求EB'的长度．
23．综合与探究
在平面直角坐标系中，如图，直线AB：y＝﹣x+3分别与x，y轴交于点A，B，点C为线段OA上一点，且．
（1）求点A坐标及直线BC的表达式；
（2）点D为x轴上一个动点，当∠CBD＝∠BAO时，求点D坐标；
（3）点M为y轴上一个动点，点N为平面内一点，当四边形ABMN是菱形时，请直接写出点N的坐标．
参考答案
一、选择题（本大题共10个小题，每小题3分，共30分.在每小题所给出的四个选项中，只有
1．用配方法解方程x2+4x+1＝0时，原方程应变形为（ ）
A．（x+2）2＝3B．（x﹣2）2＝3C．（x+2）2＝5D．（x﹣2）2＝5
【分析】先把常数项移到方程右侧，再把方程两边加上4，然后把方程作边利用完全公式表示即可．
解：x2+4x＝﹣1，
x2+4x+4＝3，
（x+2）2＝3，
故选：A．
【点评】本题考查了解一元二次方程﹣配方法：将一元二次方程配成（x+m）2＝n的形式，再利用直接开平方法求解，这种解一元二次方程的方法叫配方法．
2．已知在平行四边形ABCD中，对角线AC与BD相交于点O．添加一个条件后，平行四边形ABCD为矩形，则这个条件可以是（ ）
A．AB＝BCB．AO＝COC．AC＝BDD．AO⊥BO
【分析】由菱形的判定和矩形的判定分别对各个选项进行判断，即可得出结论．
解：A、∵平行四边形ABCD中，AB＝BC，
∴平行四边形ABCD是菱形，故选项A不符合题意；
B、平行四边形ABCD中，AO＝CO，不能判定平行四边形ABCD是矩形，故选项B不符合题意；
C、∵平行四边形ABCD中，AC＝BD，
∴平行四边形ABCD是矩形，故选项C符合题意；
D、平行四边形ABCD中，AO⊥BO，不能判定平行四边形ABCD是矩形，故选项D不符合题意；
故选：C．
【点评】此题主要考查了菱形的判定、矩形的判定以及平行四边形的性质，熟练掌握矩形的判定是解题的关键．
3．在一个不透明的布袋中装有52个白球和若干个黑球，除颜色外其他都相同，小强每次摸出一个球记录下颜色后并放回，通过多次试验后发现，摸到黑球的频率稳定在0.2左右，则布袋中黑球的个数可能有（ ）
A．11B．13C．24D．30
【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，设出未知数列出方程求解．
解：设袋中有黑球x个，
由题意得：＝0.2，
解得：x＝13，
经检验x＝13是原方程的解，
则布袋中黑球的个数可能有13个．
故选：B．
【点评】本题考查了利用频率估计概率：大量重复试验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．
4．已知，则的值为（ ）
A．B．1C．D．
【分析】直接利用已知得出a＝b，c＝b，进而代入化简即可．
解：∵，
∴a＝b，c＝b，
∴＝＝．
故选：A．
【点评】此题主要考查了比例的性质，正确将已知变形是解题关键．
5．顺次连接下列图形的各边中点，所得图形为矩形的是（ ）
①矩形；
②菱形；
③对角线相等的四边形；
④对角线互相垂直的四边形．
A．①③B．②③C．②④D．③④
【分析】连接AC、BD，根据矩形的性质得到AC＝BD，根据三角形中位线定理得到EF＝AC，FG＝BD，GH＝AC，EH＝BD，进而得到EF＝FG＝GH＝EH，根据菱形的判定定理即可判断①，进而可以判断③；根据三角形中位线定理得到EH∥BD，FG∥BD，进而证明四边形EFGH是平行四边形，根据矩形的判定定理即可判断④，进而可以判断②．
解：如图1，连接AC、BD，
∵四边形ABCD为矩形，
∴AC＝BD，
∵点E、F、G、H分别为AB、BC、CD、AD的中点，
∴EF＝AC，FG＝BD，GH＝AC，EH＝BD，
∴EF＝FG＝GH＝EH，
∴四边形EFGH为菱形，故①不符合题意；
∵矩形的对角线相等，
∴顺次连接对角线相等的四边形的中点，所得图形为菱形，故③不符合题意；
如图2，E，F，G，H分别是四边形AB，BC，CD，DA的中点，
∴EH∥BD，FG∥BD，
∴EH∥FG，
同理，EF∥HG，
∴四边形EFGH是平行四边形，
∵AC⊥BD，
∴EH⊥EF，
∴四边形EFGH是矩形，故④符合题意；
∵菱形的对角线互相垂直，
∴顺次连接菱形的各边中点，所得图形为矩形，故②符合题意；
故选：C．
【点评】本题考查的是矩形的判定与性质，菱形的性质，中点四边形，掌握三角形中位线定理、矩形的判定与性质、菱形的判定定理是解题的关键．
6．已知实数m，现甲、乙、丙、丁四人对关于x的方程（m﹣2）x2+2x﹣1＝0讨论如下，则下列判断正确的是（ ）
A．甲和丙说得对B．甲和丁说得对
C．乙和丙说得对D．乙和丁说得对
【分析】根据一元二次方程的定义对甲和乙的说法进行判断；根据根的判别式的意义对丙和丁的说法进行判断．
解：当m﹣2≠0，即m≠2时，方程（m﹣2）x2+2x﹣1＝0为一元二次方程，所以乙的判断正确；
当m﹣2＝0，即m＝2，方程（m﹣2）x2+2x﹣1＝0变形为2x﹣1＝0，此时方程为一元一次方程，所以甲的判断错误；
若m＝2，解方程2x﹣1＝0得x＝，
若m≠2，当Δ≥0时，方程（m﹣2）x2+2x﹣1＝0有两个实数根，即22﹣4（m﹣2）×（﹣1）≥0，解得m≥1且m≠2，所以丁的判定正确；
若m≠2，当Δ＜0时，方程（m﹣2）x2+2x﹣1＝0有两个实数根，即22﹣4（m﹣2）×（﹣1）＜0，解得m＜1，所以丙的判定错误．
故选：D．
【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根．
7．用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，那么可配成紫色的概率是（ ）
A．B．C．D．1
【分析】将转盘中蓝色划分为圆心角为120度的两部分，将转盘中红色也划分为圆心角为120度的两部分，画树状图列出所有等可能结果，根据概率公式求解即可．
解：根据题意画树状图如下：
由树状图可知共有9种等可能结果，其中能配成紫色的有4种结果，
那么可配成紫色的概率是，
故选：A．
【点评】本题考查列表法与树状图法求概率，解答本题的关键是明确题意，求出相应的概率．
8．在△ACB中，∠ABC＝90°，用直尺和圆规在AC上确定点D，使△BAD∽△CBD，根据作图痕迹判断，正确的是（ ）
A．B．
C．D．
【分析】若△BAD∽△CBD，可得∠ADB＝∠BDC＝90°，即BD是AC的垂线，根据作图痕迹判断即可．
解：当BD是AC的垂线时，△BAD∽△CBD．
∵BD⊥AC，
∴∠ADB＝∠CDB＝90°，
∵∠ABC＝90°，
∴∠A+∠ABD＝∠ABD+∠CBD＝90°，
∴∠A＝∠CBD，
∴△BAD∽△CBD．
根据作图痕迹可知，
A选项中，BD是∠ABC的平分线，不与AC垂直，不符合题意；
B选项中，BD是AC边上的中线，不与AC垂直，不符合题意；
C选项中，BD是AC的垂线，符合题意；
D选项中，AB＝AD，BD不与AC垂直，不符合题意．
故选：C．
【点评】本题考查尺规作图、相似三角形的判定，熟练掌握相似三角形的判定是解答本题的关键．
9．某小区新增了一家快递驿站，第一天揽件200件，第三天揽件242件，设该快递驿站揽件日平均增长率为x，根据题意平均增长率是（ ）
A．10%B．20%C．30%D．40%
【分析】利用第三天的揽件数＝第一天的揽件数×（1+该快递点这三天揽件日平均增长率）2，可列出关于x的一元二次方程，解之取其符合题意的值，即可得出结论．
解：根据题意得：200（1+x）2＝242，
解得：x1＝0.1＝10%，x2＝﹣2.1（不符合题意，舍去）．
答：该快递点这三天揽件日平均增长率为10%．
故选：A．
【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
10．如图，平行四边形ABCD中，E为AD上一点，BE交AC于点F．已知AE：ED＝2：1，则下列判断错误的是（ ）
A．△AEF与△BCF的周长比为2：3
B．△ABF与四边形EFCD的面积比为6：11
C．若连接CE，则△ABF与△CEF相似，且相似比为2：3
D．若题中条件“AE：ED＝2：1”改为“点E为边AD的黄金分割点，AE＞ED“，则＝
【分析】根据平行四边形的性质可得AD＝BC，AD∥BC，从而可得＝，再利用平行线的性质可得∠EAC＝∠ACB，∠AEF＝∠EBC，从而可得△AEF∽△CBF，进而利用相似三角形的性质即可判断A；然后利用相似三角形的性质可得＝＝，从而可得△AEF的面积：△ABF的面积＝2：3，再设△AEF的面积为4a，则△BCF的面积为9a，从而可得△ABF的面积＝6a，进而可得△ABC的面积＝15a，再利用平行四边形的性质可得AD＝BC，AB＝CD，从而利用SSS证明△ABC≌△CDA，进而可得△ABC的面积＝△ACD的面积＝15a，再利用面积的和差关系可得四边形EFCD的面积＝11a，从而可得△ABF的面积：四边形EFCD的面积比＝6：11，即可判断B；再根据相似三角形的性质可得＝，从而可得△ABF和△EFC不一定相似，即可判断C；最后根据黄金分割的定义可得＝，从而可得＝，再利用相似三角形的性质可得＝＝，从而进行计算即可判断D，即可解答．
解：∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，
∵AE：ED＝2：1，
∴＝，
∴＝，
∵AD∥BC，
∴∠EAC＝∠ACB，∠AEF＝∠EBC，
∴△AEF∽△CBF，
∴△AEF与△BCF的周长比为2：3；△AEF与△BCF的面积比为4：9；
故A不符合题意；
∵△AEF∽△CBF，
∴＝＝，
∴△AEF的面积：△ABF的面积＝2：3，
设△AEF的面积为4a，则△BCF的面积为9a，
∴△ABF的面积＝6a，
∴△ABC的面积＝△ABF的面积+△BCF的面积＝15a，
∵四边形ABCD是平行四边形，
∴AD＝BC，AB＝CD，
∵AC＝CA，
∴△ABC≌△CDA（SSS），
∴△ABC的面积＝△ACD的面积＝15a，
∴四边形EFCD的面积＝△ACD的面积﹣△AEF的面积＝11a，
∴△ABF的面积：四边形EFCD的面积比＝6：11，
故B不符合题意；
如图：连接EC，
∵△AEF∽△CBF，
∴＝，
∵∠AFB＝∠EFC，
∴△ABF和△EFC不一定相似，
故C符合题意；
∵点E为边AD的黄金分割点，AE＞ED，
∴＝，
∴＝，
∵△AEF∽△CBF，
∴＝＝，
∴＝＝＝，
故D不符合题意；
故选：C．
【点评】本题考查了相似三角形的判定与性质，平行四边形的性质，黄金分割，熟练掌握相似三角形的判定与性质，以及平行四边形的性质是解题的关键．
二、填空题（本大题共5小题，每小题3分，共15分）
11．已知x＝1是方程x2+bx﹣2＝0的一个根，则方程的另一个根是 x＝﹣2 ．
【分析】根据根与系数的关系得出x1x2＝＝﹣2，即可得出另一根的值．
解：∵x＝1是方程x2+bx﹣2＝0的一个根，
∴x1x2＝＝﹣2，
∴1×x2＝﹣2，
则方程的另一个根是：x＝﹣2，
故答案为x＝﹣2．
【点评】此题主要考查了一元二次方程根与系数的关系，得出两根之积求出另一根是解决问题的关键．
12．
如图1是液体沙漏的立体图形，上下底面平行，液体沙漏某一时刻的平面示意图如图2，图3，则图3中AB＝ cm．
【分析】根据“相似三角形的高的比等于相似比”列方程求解．
解：由题意得：上下两个三角形全等，高为6，上下底面平行，
∴，
解得：AB＝，
故答案为：．
【点评】本题考查了认识立体图形，掌握相似三角形的判定定理和性质定理是解题的关键．
13．为迎接杭州亚运会，政府计划在长为30米，宽为20米的矩形场地上修建如图所示的道路（图中的阴影部分），其余部分铺设草坪，草坪的总面积为560平方米，根据题意列出的方程为 （30﹣x）（20﹣x）＝560 ．
【分析】根据平行四边形的面积计算公式及道路的铺设方式，可得出铺设草坪的面积等于长为（30﹣x）米、宽（20﹣x）米的矩形面积，结合草坪的面积为560平方米，即可得出关于x的一元二次方程，此题得解．
解：∵道路的宽为x米，
∴铺设草坪的面积等于长为（30﹣x）米、宽（20﹣x）米的矩形面积．
∵草坪的面积为560平方米，
∴（30﹣x）（20﹣x）＝560．
故答案为：（30﹣x）（20﹣x）＝560．
【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
14．如图，已知平行四边形ABCD的面积为24，以B为位似中心，作平行四边形ABCD的位似图形平行四边形EBFG，位似图形与原图形的位似比为，连接AG、DG．则△ADG的面积为 4 ．
【分析】延长EG交CD于点H，由题意可得四边形AEHD是平行四边形，则可得此平行四边形的面积为8，从而可得△ADG的面积．
解：延长EG交CD于点H，如图，
∵四边形ABCD是平行四边形，四边形EBFG是平行四边形，
∴AB∥CD，AD∥BC；BF∥EG，
∴AD∥EG，
∴四边形AEHD是平行四边形，
∴．
∵位似图形与原图形的位似比为，
∴，
即，
∴，
∴．
故答案为：4．
【点评】本题考查了位似图形的性质，平行四边形的性质与判定，掌握这些性质是解题的关键．
15．在平面直角坐标系中，菱形OABC如图，边BC交y轴于点D，OB，AD相交于点E，点A的坐标为（6，0），∠OCB＝60°，则点E的坐标为 （2，2） ．
【分析】由菱形的性质可得OC＝BC＝OA＝AB＝4，∠OAB＝∠OCB＝60°，BC∥OA，可证△AOB和△BOC是等边三角形，由等边三角形的性质可求BD＝CD＝3，OD＝3，由相似三角形的性质可求HE，EF的长，即可求解．
解：如图，过点E作EH⊥OD于H，EF⊥OA于F，
∵四边形OABC是菱形，∠OCB＝60°，点A的坐标为（6，0），
∴OC＝BC＝OA＝AB＝4，∠OAB＝∠OCB＝60°，BC∥OA，
∴△AOB和△BOC是等边三角形，∠BDO＝∠AOD＝90°，
∴BD＝CD＝3，∠DOB＝30°，
∴OD＝3，
∵BC∥OA，
∴△BDE∽△OAE，
∴，
∴，，
∵HE∥AO，
∴＝，
∴＝，
∴HE＝2，
∵EF∥DO，
∴＝，
∴＝，
∴EF＝2，
∴点E（2，2），
故答案为：（2，2）．
【点评】本题考查菱形的性质，等边三角形的判定和性质，相似三角形判定和性质，灵活运用这些性质解决问题是解题的关键．
三、解答题（本大题共8小题，共75分.解答应写出文字说明、证明过程或演算步骤）
16．（1）3x2+8x﹣3＝0；
（2）5x2+2x﹣1＝0；
（3）2（x﹣3）2＝x2﹣9．
【分析】（1）利用因式分解法求出方程的解即可；
（2）利用公式法求出方程的解即可；
（3）利用因式分解法求出方程的解即可．
解：（1）3x2+8x﹣3＝0，
（3x﹣1）（x+3）＝0，
∴3x﹣1＝0或x+3＝0，
∴x1＝，x2＝﹣3；
（2）5x2+2x﹣1＝0，
这里a＝5，b＝2，c＝﹣1，
∴Δ＝22﹣4×5×（﹣1）＝24＞0，
∴x＝＝，
∴x1＝，x2＝；
（3）2（x﹣3）2＝x2﹣9，
2（x﹣3）2﹣（x+3）（x﹣3）＝0，
（x﹣3）[2（x﹣3）﹣（x+3）]＝0，
∴x﹣3＝0或x﹣9＝0，
∴x1＝3，x2＝9．
【点评】本题考查了解一元二次方程，能选择适当的方法解方程是解此题的关键，注意：解一元二次方程的方法有直接开平方法，公式法，配方法，因式分解法等．
17．一个不透明的口袋里装有分别标有汉字“杭”、“州”、“亚”、“运”、“会”的五个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
（1）若从中任取一个球，求摸出球上的汉字刚好是“运”的概率是 ；
（2）小华和小林商定了一个游戏规则：摇匀后随机摸出两个小球，若取出的两个球上恰好有汉字“运”则小林获胜；否则小华获胜．请用列表法或画树状图的方法说明这个游戏规则对双方是否公平．
【分析】（1）直接由概率公式求解即可；
（2）画树状图，共有20种等可能的结果，其中取出的两个球上恰好有汉字“运”的结果有8种，没有汉字“运”的结果有12种，再由概率公式求出小林获胜的概率和小华获胜的概率，即可得出结论．
解：（1）∵一个不透明的口袋里装有分别标有汉字“杭”、“州”、“亚”、“运”、“会”的五个小球，
∴从中任取一个球，求摸出球上的汉字刚好是“运”的概率是，
故答案为：；
（2）这个游戏规则对双方不公平，理由如下：
画树状图如下：
共有20种等可能的结果，其中取出的两个球上恰好有汉字“运”的结果有8种，没有汉字“运”的结果有12种，
∴小林获胜的概率＝＝，小华获胜的概率＝＝，
∴小林获胜的概率≠小华获胜的概率，
∴这个游戏规则对双方不公平．
【点评】此题考查了游戏公平性的判断以及列表法与树状图法求概率，判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率＝所求情况数与总情况数之比．
18．如图，四边形ABCD中，∠ABC＝90°，AD∥BC，AD＝BC，点E是AD上一点，连接BE，CE，且∠BEC＝90°，点F是BC的中点．
（1）求证：四边形ABCD是矩形；
（2）若∠ECD＝30°，EF＝4，求矩形的面积．
【分析】（1）根据有一个角是直角的平行四边形是矩形即可解决问题；
（2）根据直角三角形斜边上的中线等于斜边的一半得BF＝CF＝EF＝4，得BC＝8，证明△CEF是等边三角形，得CD＝ED＝2，然后利用矩形面积公式即可解决问题．
【解答】（1）证明：∵AD∥BC，AD＝BC，
∴四边形ABCD是平行四边形，
∵∠ABC＝90°，
∴四边形ABCD是矩形；
（2）解：∵∠BEC＝90°，点F是BC的中点，
∴BF＝CF＝EF＝4，
∴BC＝8，
∵∠ECD＝30°，∠BCD＝90°，
∴∠BCE＝60°，
∴△CEF是等边三角形，
∴EC＝EF＝4，
∴ED＝EC＝2，
∴CD＝ED＝2，
∴矩形的面积＝BC•CD＝8×2＝16．
【点评】本题考查了矩形的判定与性质，等边三角形的判定，直角三角形斜边上的中线，平行四边形的判定与性质，解决本题的关键是掌握矩形的性质．
19．某超市销售一种衬衫．平均每天可售出20件，每件盈利40元．为了扩大销售、增加盈利，该超市准备适当降价，经过一段时间测算，发现每件衬衫每降低1元，平均每天可多售出2件．
（1）在每件盈利不少于25元的前提下，要使该衬衫每天销售获利为1200元，问每件衬衫应降价多少元？
（2）小明的观点：“该衬衫每天的销售获利能达到1300元”，你同意小明的观点吗？若同意，请求出每件衬衫应降价多少元？若不同意，请说明理由．
【分析】（1）设每件衬衫应降价x元，根据能使商场每天盈利1200元列一元二次方程，求解即可；
（2）设每件衬衫应降价m元，根据商场每天盈利1300元列一元二次方程，求解即可．
解：（1）设每件衬衫应降价x元，
根据题意，得（40﹣x）（20+2x）＝1200，
解得x1＝10，x2＝20（舍去）．
答：每件衬衫应降价10元；
（2）不同意，理由如下：
设每件衬衫应降价m元，能使商场每天盈利1300元，
根据题意，得（40﹣m）（20+2m）＝1300，
化简得m2﹣30m+250＝0，
∵Δ＝900﹣4×1×250＝﹣100＜0，
∴原方程没有实数解，
∴商场每天的盈利不可能达到1300元．
【点评】本题考查了一元二次方程的应用，根据题意建立等量关系是解题的关键．
20．数学思想方法作为数学学科的一般原理，在数学学习中至关重要．我们经常运用转化、类比、数形结合、从特殊到一般等思想方法来解决一些数学问题．
如图①，在平行四边形ABCD中，点E是AB边的中点，点G是线段BC上一点，AG与DE相交于点F．若，求的值．
【尝试探究】在图①中，过点E作EH∥AD交AG于点H，则的值为 3 ，的值为 2 的值为 ．
【类比延伸】如图②，在①的条件下，若，则的值为 （用含a的代数式表示）．
【拓展迁移】如图③，在平行四边形ABCD中，点E是AB边的中点，若点G在线段CB的延长线上，AG交DE的延长线于点F，若，则的值为 （用含m的代数式表示）．
【分析】【尝试探究】由点E是AB边的中点，得AB＝2AE，由平行四边形的性质得BC＝AD，BC∥AD，则△AFD∽△HFE，得＝＝3，则BC＝AD＝3EH，再证明△ABG∽△AEH，得＝＝2，所以BG＝2EH，则＝，于是得到问题的答案；
【类比延伸】作EL∥AD交AG于点L，则△AFD∽△LFE，得＝＝a，则BC＝AD＝a•EL，再证明△ABG∽△AEL，得＝＝2，所以BG＝2EL，则＝，于是得到问题的答案；
【拓展迁移】作EI∥DA交AG于点I，则△ADF∽△IEF，得＝＝m，则BC＝DA＝m•EI，再证明△ABG∽△AEI，得＝＝2，所以BG＝2EI，则＝，于是得到问题的答案．
解：【尝试探究】如图①，∵点E是AB边的中点，
∴AE＝BE，
∴AB＝2AE，
∵四边形ABCD是平行四边形，＝3，
∴BC＝AD，BC∥AD，
∴AD∥EH，
∴△AFD∽△HFE，
∴＝＝3，
∴BC＝AD＝3EH，
∴BG∥AD，EH∥AD，
∴BG∥EH，
∴△ABG∽△AEH，
∴＝＝2，
∴BG＝2EH，
∴＝＝，
故答案为：3，2，．
【类比延伸】如图②，作EL∥AD交AG于点L，
∵AD∥EL，＝a，
∴△AFD∽△LFE，
∴＝＝a，
∴BC＝AD＝a•EL，
∴BG∥AD，EL∥AD，
∴BG∥EL，
∴△ABG∽△AEL，
∴＝＝2，
∴BG＝2EL，
∴＝＝，
故答案为：．
【拓展迁移】如图③，作EI∥DA交AG于点I，
∵DA∥EI，＝m，
∴△ADF∽△IEF，
∴＝＝m，
∴BC＝DA＝m•EI，
∵BG∥DA，EI∥DA，
∴BG∥EI，
∴△ABG∽△AEI，
∴＝＝2，
∴BG＝2EI，，
∴＝＝，
故答案为：．
【点评】此题重点考查线段中点的定义、平行线边形的性质、相似三角形的判定与性质、数形结合与类比、转化数学思想的运用等知识与方法，此题综合性强，难度较大，正确地作出辅助线构造相似三角形是解题的关键．
21．操作与探究
【操作】在数学实践课上，老师要求同学们对如图1的△ABC纸片进行以下操作，并探究其中的问题：
第一步：如图2，沿过点B的直线折叠，使得点A落在BC上，展开铺平该纸片，折痕为BD；
第二步：如图3，继续折叠该纸片，使得点B与点D重合，展开铺平该纸片，折痕为EF；
第三步：如图4，连接DE，DF．
【探究】
任务一：判断四边形BEDF的形状，并说明理由；
任务二：在△ABC纸片中，若∠ABC＝60°，折痕EF＝2，四边形BEDF的面积为 2 ．
【分析】任务一：设EF交BD于点I，由折叠得∠ABD＝∠CBD，点D与点B关于直线EF对称，则EF垂直平分BD，所以∠BIE＝∠BIF＝90°，DE＝BE，DF＝BF，可根据“ASA”证明△BEI≌△BFI，得BE＝BF，则DE＝BE＝BF＝DF，即可根据“四条边都相等的四边形是菱形”证明四边形BEDF是菱形；
任务二：由∠ABC＝60°，BE＝BF，证明△BEF是等边三角形，则BE＝EF＝2，由菱形的性质得EI＝FI＝EF＝1，BI＝DI，而∠BIE＝90°，即可根据勾股定理求得BI＝＝，则BD＝2BI＝2，则S四边形BEDF＝BD•EF＝2，于是得到问题的答案．
解：任务一：四边形BEDF是菱形，
理由：如图4，设EF交BD于点I，
∵将△ABC沿过点B的直线折叠，使得点A落在BC上，
∴∠ABD＝∠CBD，
∵将△ABC折叠，使点B与点D重合，折痕为EF，
∴点D与点B关于直线EF对称，
∴EF垂直平分BD，
∴∠BIE＝∠BIF＝90°，DE＝BE，DF＝BF，
在△BEI和△BFI中，
，
∴△BEI≌△BFI（ASA），
∴BE＝BF，
∴DE＝BE＝BF＝DF，
∴四边形BEDF是菱形．
任务二：如图4，∵∠ABC＝60°，BE＝BF，
∴△BEF是等边三角形，
∴BE＝EF＝2，
∵四边形BEDF是菱形，
∴EI＝FI＝EF＝1，BI＝DI，
∵EF⊥BD，
∴∠BIE＝90°，
∴BI＝＝＝，
∴BD＝2BI＝2，
∴S四边形BEDF＝BD•EF＝×2×2＝2，
故答案为：2．
【点评】此题重点考查轴对称的性质、线段的垂直平分线的性质、全等三角形的判定与性质、菱形的判定与性质、等边三角形的判定与性质、勾股定理、菱形的面积公式等知识，此题综合性强，难度较大，设EF交BD于点I，证明△BEI≌△BFI是解题的关键．
22．综合与实践
【模型探索】如图1，在正方形ABCD中，点E，F分别在边DC，BC上，若AF⊥BE，则AF与BE的数量关系为 AF＝BE ．
【模型应用】如图2，将边长为2的正方形ABCD折叠，使点B落在CD边的中点E处，点A落在点F处，折痕交AD于点M，交BC于点N，则线段MN的长度是 ．
【知识迁移】如图3，在矩形ABCD中，AB＝2，BC＝3，点E在边CD上，点P，Q分别在边AD，BC上，且 AE⊥PQ，则的值为 ．
【综合应用】如图4，正方形ABCD的边长为12，点F是BC上一点，将△ABF沿AF折叠，使点B落在点B'处，连接BB'并延长交CD于点E．若CE＝5，求EB'的长度．
【分析】【模型探索】根据“SAS”可证△ABF≌△BCE，根据全等三角形的性质得出AF＝BE；
【模型应用】如图2，连接BE，过C作CP∥MN交AD于P，根据轴对称的性质得到BE⊥MN，根据勾股定理得到BE＝＝；由【模型探索】知CP＝BE＝，根据平行四边形的性质即可得到结论；
【知识迁移】根据矩形的性质得到∠D＝90°，如图3，过Q作QH⊥AD于H，根据矩形的性质得到HQ＝AB＝2，根据相似三角形的性质即可得到结论；
【综合应用】根据勾股定理得到BE＝＝13，根据轴对称的性质得到BE⊥AF于H，BB′＝2BH，由【模型探索】知，AF＝BE＝13，BF＝CE＝5，根据三角形的面积公式即可得到结论．
解：【模型探索】AF＝BE；
理由：∵四边形ABCD是正方形，
∴AB＝BC，∠ABC＝∠BCD＝90°，
∵BF＝CE，
∴△ABF≌△BCE（SAS），
∴AF＝BE，
故答案为：AF＝BE；
【模型应用】如图2，连接BE，过C作CP∥MN交AD于P，
∵将边长为2的正方形ABCD折叠，使点B落在CD边的中点E处，
∴点B与点E关于MN对称，
∴BE⊥MN，
∴CP⊥BE，
∵点E是CD边的中点，
∴CE＝CD＝1，
∴BE＝＝，
由【模型探索】知CP＝BE＝，
∵AD∥BC，CP∥MN，
∴四边形CPMN是平行四边形，
∴MN＝CP＝，
故答案为：；
【知识迁移】∵四边形ABCD是矩形，
∴∠D＝90°，
如图3，过Q作QH⊥AD于H，
则四边形ABQH是矩形，
∴HQ＝AB＝2，
∵AE⊥PQ，
∴∠PAE+∠APQ＝∠PQH+∠QPH＝90°，
∴∠DAE＝∠PQH，
∵∠D＝∠QHP＝90°，
∴△ADE∽△QHP，
∴＝，
故答案为：．
【综合应用】∵四边形ABCD是正方形，
∴∠C＝90°，
∵BC＝12，CE＝5，
∴BE＝＝13，
∵将△ABF沿AF折叠，使点B落在点B'处，
∴点B与点B′关于AF对称，
∴BE⊥AF于H，BB′＝2BH，
由【模型探索】知，AF＝BE＝13，BF＝CE＝5，
∵S△ABF＝，
∴BH＝＝＝，
∴BB′＝，
∴EB′＝13﹣＝．
【点评】本题是相似形的综合题，考查了相似三角形的判定和性质，矩形的性质，正方形的性质，全等三角形的判定和性质，正确地作出辅助线是解题的关键．
23．综合与探究
在平面直角坐标系中，如图，直线AB：y＝﹣x+3分别与x，y轴交于点A，B，点C为线段OA上一点，且．
（1）求点A坐标及直线BC的表达式；
（2）点D为x轴上一个动点，当∠CBD＝∠BAO时，求点D坐标；
（3）点M为y轴上一个动点，点N为平面内一点，当四边形ABMN是菱形时，请直接写出点N的坐标．
【分析】（1）求出A、B、C点坐标，再用待定系数法求函数的解析式即可；
（2）设D（t，0），分两种情况讨论：当D点在C点右侧时，过点D作DE⊥BD交BC延长线于点E，过点D作GF⊥x轴，过点B作BG⊥GF交于G点，过点E作EF⊥GF交于点F，通过证明△BDG≌△DEF（AAS），求出点E（t﹣3，﹣t），再将点E代入直线BC的解析式，求出t的值即可求D点坐标；当D点在C点的左侧时，同理可求E（3+t，t），再将点E代入直线BC的解析式，求出t的值即可求D点坐标；
（3）设M（0，m），根据菱形的性质，分情况求出m的值，即可得点N的坐标．
解：（1）令x＝0，则y＝3，令y＝0，则x＝3，
∴B（0，3），A（3，0），
∴OA＝3，
∵＝2，
∴AC＝2CO，
∴AC＝2，CO＝1，
∴C（1，0），
设直线BC的表达式为y＝kx+b，
∴，解得，
∴直线BC的表达式为y＝﹣3x+3；
（2）∵B（0，3），A（3，0），
∴OA＝OB＝3，
∴∠BAO＝45°，
设D（t，0），
当D点在C点右侧时，如图1，
过点D作DE⊥BD交BC延长线于点E，过点D作GF⊥x轴，过点B作BG⊥GF交于G点，过点E作EF⊥GF交于点F，
∵∠BDE＝90°，
∴∠BDG+∠EDF＝90°，
∵∠BDG+∠DBG＝90°，
∴∠EDF＝∠DBG，
∵∠CBD＝∠BAO＝45°，
∴BD＝DE，
∴△BDG≌△DEF（AAS），
∴BG＝DF＝t，GD＝EF＝3，
∴E（t﹣3，﹣t），
∴﹣3（t﹣3）+3＝﹣t，
解得t＝6，
∴D（6，0）；
当D点在C点的左侧时，如图2，
同理可求E（3+t，t），
∴﹣3（3+t）+3＝t，
解得t＝﹣，
∴D（﹣，0）；
综上所述：D点坐标为（6，0）或（﹣，0）；
（3）设M（0，m），
当四边形ABMN是菱形，AM为菱形的对角线时，AB＝AN，AN∥BM，
∵B（0，3），A（3，0），
∴AB＝3，
∴M（0，3﹣3）或（0，3+3），
∴点N的坐标为（3，﹣3）或（3，3）．
【点评】本题是一次函数综合题，考查一次函数的图象及性质，熟练掌握一次函数的图象及性质，菱形的性质，等腰直角三角形的性质，三角形全等的判定及性质是解题的关键．
甲：该方程一定是关于x的一元二次方程
乙：该方程有可能是关于x的一元二次方程
丙：当m≤1时，该方程没有实数根
丁：当m≥1且m≠2时，该方程有两个实数根
甲：该方程一定是关于x的一元二次方程
乙：该方程有可能是关于x的一元二次方程
丙：当m≤1时，该方程没有实数根
丁：当m≥1且m≠2时，该方程有两个实数根