

浙江省温州市瑞安市五校联考2023-2024学年九年级上学期12月期末数学试题
展开请你认真审题,积极思考,细心答题,发挥最佳水平。答题时,请注意以下几点:
1.全卷共4页,有三大题,24小题.全卷满分120分.考试时间120分钟.
2.答案必须写在答题纸相应的位置上,写在试题卷、草稿纸上均无效。
3.答题前,认真阅读答题纸上的《注意事项》,按规定答题.
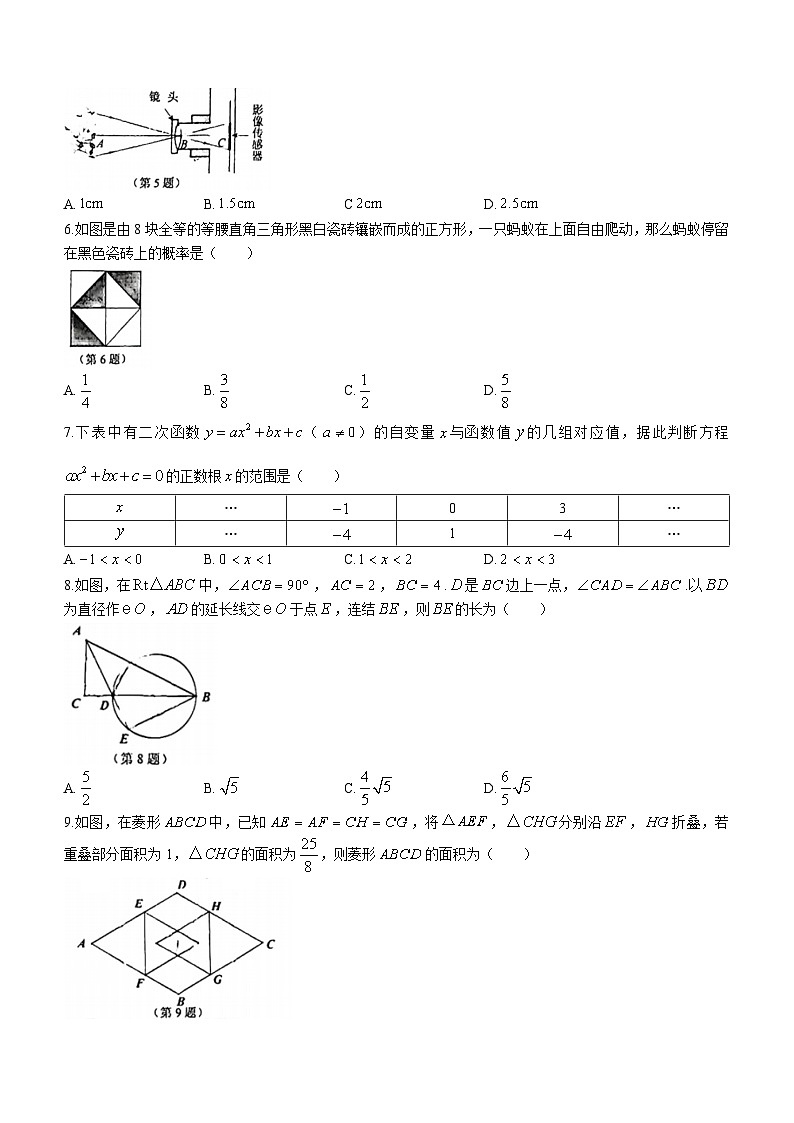
试卷Ⅰ
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
1.一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同,若从中任意摸出一个球,则下列叙述正确的是( )
A.摸到红球是必然事件B.摸到白球是不可能事件
C.摸到红球与白球的可能性相等D.摸到红球比摸到白球的可能性大
2.抛物线的顶点坐标是( )
A.B.C.D.
3.如图,在中,,分别是边,上的点,,则下列比例式中正确的是( )
A.B.C.D
4.如图,在矩形中,,,若以点为圆心,以4为半径作,则下列各点在外的是( )
A.点B.点C.点D.点
5.如图,一朵小花到照相机镜头的距离为;镜头到传感器的距离为.若小花高,则小花在传感器上的高度为( )
A.B.CD.
6.如图是由8块全等的等腰直角三角形黑白瓷砖镶嵌而成的正方形,一只蚂蚁在上面自由爬动,那么蚂蚁停留在黑色瓷砖上的概率是( )
A.B.C.D.
7.下表中有二次函数()的自变量与函数值的几组对应值,据此判断方程的正数根的范围是( )
A.B.C.D.
8.如图,在中,,,.是边上一点,.以为直径作,的延长线交于点,连结,则的长为( )
A.B.C.D.
9.如图,在菱形中,已知,将,分别沿,折叠,若重叠部分面积为1,的面积为,则菱形的面积为( )
A.8B.C.16D.
10.如图1,点,分别是线段的三等分点,以为直径作半圆,过点作的垂线交半圆于点,以与的和为边作正方形,以与的和为边作正方形与正方形,若图中阴影部分面积为8,则的长为( )
A.B.4C.D.
卷Ⅱ
二、填空题(本题有8小题,每题4分,共32分)
11.若,则*.
12.将二次函数的解析式化成的形式为*.
13.已知一个扇形的面积是,圆心角等于,这个扇形的弧长为*.
14.如图1是由若干个相似直角三角形组成的美妙螺旋线,选择其中两个相邻的直角三角形如图2所示.若,,,则的长为*.
15.如图,以正六边形的一边为公共边,在正六边形内部作正五边形,连结,则*°.
16.如图、是的直径、点是半径的中点,过点作,交于点、两点,过点作直径,连结,则*.
17.如图,点为三角形纸片的重心,过点分别作,,的平行线,沿着平行线剪开得到与.若的面积为9,则与的面积之和为*.
18.如图、灌溉系统从点处喷出水来给右侧矩形花坛浇水,水流的形状为抛物线某一时刻、抛物线经过点,分别交,于点,.测量得,,,,则*.过一段时间,灌溉系统由点处升高至点处,水流的方向和水量均没有发生变化,此时抛物线经过点,则*.
三、解答题(本题有6小题,共58分,解答需写出必要的文字说明、演算步骤或证明过程)
19.(本题8分)有三张分别标有数字2,7,9的卡片,它们的背面都相同,现将它们背面朝上,从中任意抽出一张卡片,放回,再从卡片里任意抽出一张.
(1)请用树状图或列表法表示出所有可能的结果;
(2)求两张卡片的数字之和为偶数的概率.
20.(本题8分)如图,在的方格纸中,已知格点与格点,请按要求画与相似的格点三角形(顶点均在格点上),要求图1与图2所画的三角形不全等.
(1)在图1中画,使点,均落在的边上.
(2)在图2中画,使点在的内部(不包括边上,且与组成一幅轴对称的图形.
21.(本题8分)在平面直角坐标系中,抛物线的表示式为().
(1)当时,求的值.
(2)将抛物线向左平移两个单位后,恰经过点,求的值.
22.(本题10分)如图,已知是锐角的外接圆,,是的直径,是边上的高,连结.
(1)求证:.
(2)若,,求的长.
23.(本题12分)为了确定大货车能否通过公路隧道,道路交通学习小组展开了以下研究.
24.(本题12分)如图,在矩形中,,在的延长线上取点,射线与射线交于点,点关于直线的对称点记为点,连结并延长交的延长线于点.设,,已知.
(1)求与的长.
(2)记,,的面积分别为,,,且,求的值.
(3)连结,若与以,,为顶点的三角形相似,求的值.
2024届九年级阶段性学习品质调研---数学参考答案
一、选择题(本题有10小题,每小题3分,共30分)
二、填空题(本题有8小题,每小题4分,共32分)
三、解答题(本题有6小题,共58分)
19.(本题8分)
(1) 4分
(2)两次摸到数字和为偶数的结果有5种
P(两次摸到数字和为偶数) 4分
20.(本题8分)每小题4分,答案不唯一,具体如下:
解:(1)
(2)
21.(本题8分)解:(1)当时, (4分)
(2)方法1:由(1)可知,原抛物线经过
∵将抛物线向左平移2个单位后,恰经过点
∴原抛物线对称轴为直线
∴ (2分)
∴ (2分)
方法2:∵将抛物线向左平移2个单位后,恰经过点
∴原抛物线经过 (2分)
代入解析式可得: (2分)
∴ (2分)
方法3:将抛物线向左平移2个单位后,可得 (2分)
代入可得:
∴ (2分)
22.(本题10分)
(1)∵是的直径 ∴ (1分)
∵是边上的高 ∴ (1分)
∵ (1分)
∴ (1分)
∴ (1分)
(2)∵,, ∴ (1分)
∵ ∴ (1分)
∴ (1分)
∵ (1分)
∴ (2分)
23.(本题12分)
(1) (4分,画法不唯一)
(2)过点作交于点,交于点
令,则,,(1分)
∵,,
∴,
∵
∴(2分)
解得:
∴(1分)
(3)构造,且
过点作于点
∴,(2分)
∵(1分)
∴大货车能通过该隧道(1分)
24.(本题12分)
解:(1)在矩形中,,,,,
∴,,"
∴,(1分)
∴,
即,
∴,
即.(1分)
∵,∴,(1分)
∴.(1分)
(2)∵点与点关于直线对称,
∴,,
∴.
∵,∴.
∵,∴,
∴.∵,
∴,
∴.(1分)
∵,,∴,(1分)
∴,即,解得,(1分)
∴.(1分)
(3)∵,
∴,
∴,
∴.
①当时,.
∵,,,
∴,
∴,
∴,
∴,
∴.(2分)
②当时,.
∵,,,
∴,
∴,
∴.
∴,
∴,
∴.(2分)
综上所述,或.
…
0
3
…
…
1
…
材料收集
材料1
材料2
材料3
如图1某一公路单向隧道由一弧形拱与矩形组成,经测量得,
如图2,为了确定弧形拱的圆心与半径,学习小组找到一根长的笔直杆子,调整杆子位置直至点在上,点在圆弧上,,.
如图3,某一集装箱大货车宽为,高为,停在隧道口.
问题解决
任务1
确定圆心位置:利用直尺与图规确定圆心的位置(保留作图痕迹)
任务2
确定弧形拱半径:求出弧形拱的半径
任务3
确定车辆通过可能:通过计算说明该货车能否通过隧道.
1
2
3
4
5
6
7
8
9
10
D
A
D
C
C
B
D
D
C
C
11
12
13
14
15
16
17
18
84°
30°
5
10,
2023-2024学年浙江省温州市瑞安市西部联盟联考九年级上学期12月月考数学试题: 这是一份2023-2024学年浙江省温州市瑞安市西部联盟联考九年级上学期12月月考数学试题,文件包含浙江省温州市瑞安市西部联盟联考九年级上学期12月月考数学试题原卷版docx、浙江省温州市瑞安市西部联盟联考九年级上学期12月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
2023-2024学年浙江省温州市瑞安市四校联考数学九上期末复习检测模拟试题含答案: 这是一份2023-2024学年浙江省温州市瑞安市四校联考数学九上期末复习检测模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下列判断正确的是,下列图形中,是中心对称图形的是等内容,欢迎下载使用。
2023-2024学年浙江省温州市瑞安市四校联考数学九年级第一学期期末综合测试试题含答案: 这是一份2023-2024学年浙江省温州市瑞安市四校联考数学九年级第一学期期末综合测试试题含答案,共8页。试卷主要包含了方程的根的情况等内容,欢迎下载使用。












