2017年黑龙江省鹤岗市中考数学试题及答案

这是一份2017年黑龙江省鹤岗市中考数学试题及答案，共28页。试卷主要包含了填空题，选择题，解答题等内容，欢迎下载使用。
一、填空题（每题3分，满分30分）
1．在2017年的“双11”网上促销活动中，淘宝网的交易额突破了3200000000元，将数字3200000000用科学记数法表示 ．
2．函数y=中，自变量x的取值范围是 ．
3．如图，BC∥EF，AC∥DF，添加一个条件 ，使得△ABC≌△DEF．
4．在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球，任意摸出一球，摸到红球的概率是 ．
5．不等式组的解集是x＞﹣1，则a的取值范围是 ．
6．原价100元的某商品，连续两次降价后售价为81元，若每次降低的百分率相同，则降低的百分率为 ．
7．如图，边长为4的正方形ABCD，点P是对角线BD上一动点，点E在边CD上，EC=1，则PC+PE的最小值是 ．
8．圆锥底面半径为3cm，母线长3cm则圆锥的侧面积为 cm2．
9．△ABC中，AB=12，AC=，∠B=30°，则△ABC的面积是 ．
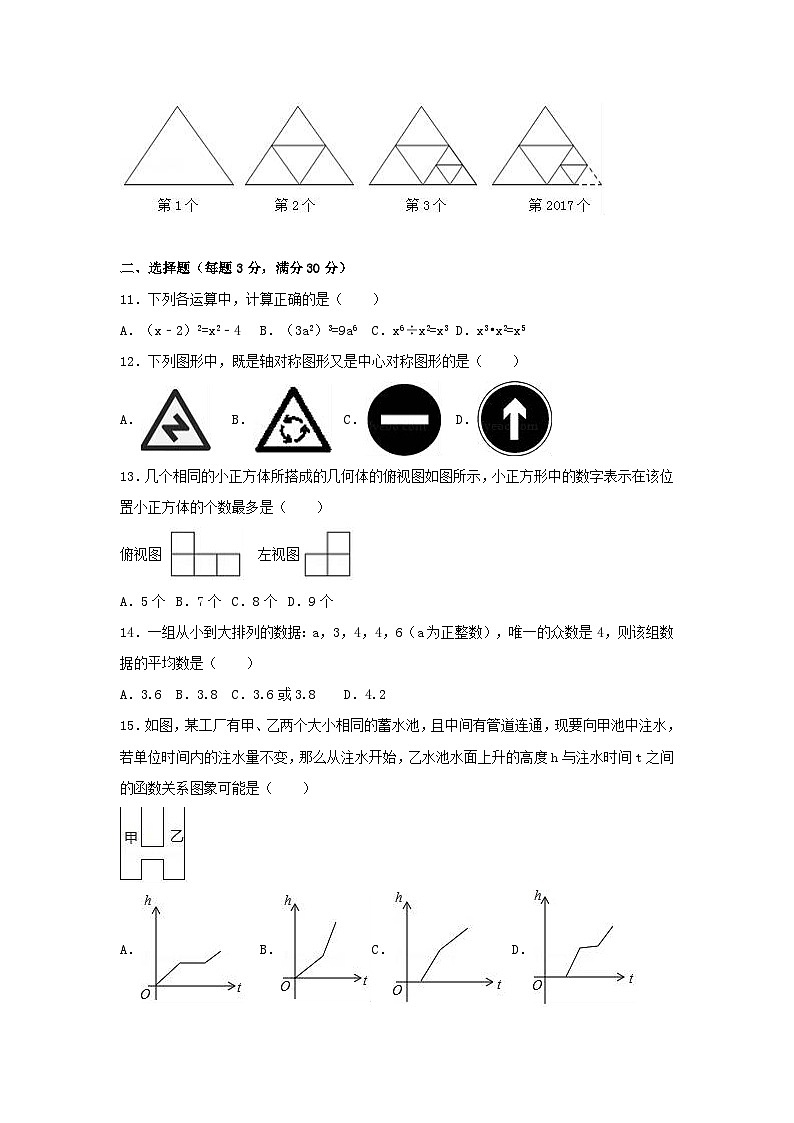
10．观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…．则第2017个图形中有 个三角形．

二、选择题（每题3分，满分30分）
11．下列各运算中，计算正确的是（ ）
A．（x﹣2）2=x2﹣4B．（3a2）3=9a6C．x6÷x2=x3D．x3•x2=x5
12．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
13．几个相同的小正方体所搭成的几何体的俯视图如图所示，小正方形中的数字表示在该位置小正方体的个数最多是（ ）
俯视图 左视图
A．5个B．7个C．8个D．9个
14．一组从小到大排列的数据：a，3，4，4，6（a为正整数），唯一的众数是4，则该组数据的平均数是（ ）
A．3.6B．3.8C．3.6或3.8D．4.2
15．如图，某工厂有甲、乙两个大小相同的蓄水池，且中间有管道连通，现要向甲池中注水，若单位时间内的注水量不变，那么从注水开始，乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是（ ）
A．B．C．D．
16．若关于x的分式方程的解为非负数，则a的取值范围是（ ）
A．a≥1B．a＞1C．a≥1且a≠4D．a＞1且a≠4
17．在平行四边形ABCD中，∠A的平分线把BC边分成长度是3和4的两部分，则平行四边形ABCD周长是（ ）
A．22B．20C．22或20D．18
18．如图，是反比例函数y1=和一次函数y2=mx+n的图象，若y1＜y2，则相应的x的取值范围是（ ）
A．1＜x＜6B．x＜1C．x＜6D．x＞1
19．某企业决定投资不超过20万元建造A、B两种类型的温室大棚．经测算，投资A种类型的大棚6万元/个、B种类型的大棚7万元/个，那么建造方案有（ ）
A．2种B．3种C．4种D．5种
20．如图，在边长为4的正方形ABCD中，E、F是AD边上的两个动点，且AE=FD，连接BE、CF、BD，CF与BD交于点G，连接AG交BE于点H，连接DH，下列结论正确的个数是（ ）
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG：S△HBG=tan∠DAG ⑤线段DH的最小值是2﹣2．
A．2B．3C．4D．5

三、解答题（满分60分）
21．先化简，再求值：（﹣）÷，请在2，﹣2，0，3当中选一个合适的数代入求值．
22．如图，在平面直角坐标系中，Rt△ABC三个顶点都在格点上，点A、B、C的坐标分别为A（﹣1，3），B（﹣3，1），C（﹣1，1）．请解答下列问题：
（1）画出△ABC关于y轴对称的△A1B1C1，并写出B1的坐标．
（2）画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1，并求出点A1走过的路径长．
23．如图，已知抛物线y=﹣x2+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=﹣x+3交于C、D两点．连接BD、AD．
（1）求m的值．
（2）抛物线上有一点P，满足S△ABP=4S△ABD，求点P的坐标．
24．某校在艺术节选拔节目过程中，从备选的“街舞”、“爵士”、“民族”、“拉丁”四种类型舞蹈中，选择一种学生最喜爱的舞蹈，为此，随机调查了本校的部分学生，并将调查结果绘制成如下统计图表（每位学生只选择一种类型），根据统计图表的信息，解答下列问题：
（1）本次抽样调查的学生人数及a、b的值．
（2）将条形统计图补充完整．
（3）若该校共有1500名学生，试估计全校喜欢“拉丁舞蹈”的学生人数．
25．为营造书香家庭，周末小亮和姐姐一起从家出发去图书馆借书，走了6分钟忘带借书证，小亮立即骑路边共享单车返回家中取借书证，姐姐以原来的速度继续向前行走，小亮取到借书证后骑单车原路原速前往图书馆，小亮追上姐姐后用单车带着姐姐一起前往图书馆．已知单车的速度是步行速度的3倍，如图是小亮和姐姐距家的路程y（米）与出发的时间x（分钟）的函数图象，根据图象解答下列问题：
（1）小亮在家停留了 分钟．
（2）求小亮骑单车从家出发去图书馆时距家的路程y（米）与出发时间x（分钟）之间的函数关系式．
（3）若小亮和姐姐到图书馆的实际时间为m分钟，原计划步行到达图书馆的时间为n分钟，则n﹣m= 分钟．
26．在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．
旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）
若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．
27．由于雾霾天气频发，市场上防护口罩出现热销．某药店准备购进一批口罩，已知1个A型口罩和3个B型口罩共需26元；3个A型口罩和2个B型口罩共需29元．
（1）求一个A型口罩和一个B型口罩的售价各是多少元？
（2）药店准备购进这两种型号的口罩共50个，其中A型口罩数量不少于35个，且不多于B型口罩的3倍，有哪几种购买方案，哪种方案最省钱？
28．如图，矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上，线段OA、OC的长度满足方程|x﹣15|+=0（OA＞OC），直线y=kx+b分别与x轴、y轴交于M、N两点，将△BCN沿直线BN折叠，点C恰好落在直线MN上的点D处，且tan∠CBD=
（1）求点B的坐标；
（2）求直线BN的解析式；
（3）将直线BN以每秒1个单位长度的速度沿y轴向下平移，求直线BN扫过矩形AOCB的面积S关于运动的时间t（0＜t≤13）的函数关系式．

2017年黑龙江省鹤岗市中考数学试题
参考答案与试题解析

一、填空题（每题3分，满分30分）
1．在2017年的“双11”网上促销活动中，淘宝网的交易额突破了3200000000元，将数字3200000000用科学记数法表示 3.2×109 ．
【考点】1I：科学记数法—表示较大的数．
【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．
【解答】解：3200000000=3.2×109．
故答案为：3.2×109．

2．函数y=中，自变量x的取值范围是 x＞1 ．
【考点】E4：函数自变量的取值范围；62：分式有意义的条件；72：二次根式有意义的条件．
【分析】根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0可求出自变量x的取值范围．
【解答】解：根据题意得：x﹣1＞0，
解得：x＞1．

3．如图，BC∥EF，AC∥DF，添加一个条件 AB=DE或BC=EF或AC=DF ，使得△ABC≌△DEF．
【考点】KB：全等三角形的判定．
【分析】本题要判定△ABC≌△DEF，易证∠A=∠EDF，∠ABC=∠E，故添加AB=DE、BC=EF或AC=DF根据ASA、AAS即可解题．
【解答】解：∵BC∥EF，
∴∠ABC=∠E，
∵AC∥DF，
∴∠A=∠EDF，
∵在△ABC和△DEF中，，
∴△ABC≌△DEF，
同理，BC=EF或AC=DF也可求证△ABC≌△DEF．
故答案为AB=DE或BC=EF或AC=DF均可．

4．在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球，任意摸出一球，摸到红球的概率是 ．
【考点】X4：概率公式．
【分析】根据随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数，用红球的个数除以总个数，求出恰好摸到红球的概率是多少即可．
【解答】解：∵袋子中共有8个球，其中红球有3个，
∴任意摸出一球，摸到红球的概率是，
故答案为：．

5．不等式组的解集是x＞﹣1，则a的取值范围是 a≤﹣ ．
【考点】CB：解一元一次不等式组．
【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了，结合不等式组的解集即可确定a的范围．
【解答】解：解不等式x+1＞0，得：x＞﹣1，
解不等式a﹣x＜0，得：x＞3a，
∵不等式组的解集为x＞﹣1，
则3a≤﹣1，
∴a≤﹣，
故答案为：a≤﹣．

6．原价100元的某商品，连续两次降价后售价为81元，若每次降低的百分率相同，则降低的百分率为 10% ．
【考点】AD：一元二次方程的应用．
【分析】先设平均每次降价的百分率为x，得出第一次降价后的售价是原来的（1﹣x），第二次降价后的售价是原来的（1﹣x）2，再根据题意列出方程解答即可．
【解答】解：设这两次的百分率是x，根据题意列方程得
100×（1﹣x）2=81，
解得x1=0.1=10%，x2=1.9（不符合题意，舍去）．
答：这两次的百分率是10%．
故答案为：10%．

7．如图，边长为4的正方形ABCD，点P是对角线BD上一动点，点E在边CD上，EC=1，则PC+PE的最小值是 5 ．
【考点】PA：轴对称﹣最短路线问题；LE：正方形的性质．
【分析】连接AC、AE，由正方形的性质可知A、C关于直线BD对称，则AE的长即为PC+PE的最小值，再根据勾股定理求出AE的长即可．
【解答】解：连接AC、AE，
∵四边形ABCD是正方形，
∴A、C关于直线BD对称，
∴AE的长即为PC+PE的最小值，
∵CD=4，CE=1，
∴DE=3，
在Rt△ADE中，
∵AE===5，
∴PC+PE的最小值为5．
故答案为：5．

8．圆锥底面半径为3cm，母线长3cm则圆锥的侧面积为 9π cm2．
【考点】MP：圆锥的计算．
【分析】根据题意可求出圆锥底面周长，然后利用扇形面积公式即可求出圆锥的侧面积．
【解答】解：圆锥的底面周长为：2π×3=6π，
∴圆锥侧面展开图的弧长为：6π，
∵圆锥的母线长3，
∴圆锥侧面展开图的半径为：3
∴圆锥侧面积为：×3×6π=9π；
故答案为：9π；

9．△ABC中，AB=12，AC=，∠B=30°，则△ABC的面积是 21或15 ．
【考点】T7：解直角三角形．
【分析】过A作AD⊥BC于D（或延长线于D），根据含30度角的直角三角形的性质得到AD的长，再根据勾股定理得到BD，CD的长，再分两种情况：如图1，当AD在△ABC内部时、如图2，当AD在△ABC外部时，进行讨论即可求解．
【解答】解：①如图1，作AD⊥BC，垂足为点D，
在Rt△ABD中，∵AB=12、∠B=30°，
∴AD=AB=6，BD=ABcsB=12×=6，
在Rt△ACD中，CD===，
∴BC=BD+CD=6+=7，
则S△ABC=×BC×AD=×7×6=21；
②如图2，作AD⊥BC，交BC延长线于点D，
由①知，AD=6、BD=6、CD=，
则BC=BD﹣CD=5，
∴S△ABC=×BC×AD=×5×6=15，
故答案为：21或15．

10．观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…．则第2017个图形中有 8065 个三角形．
【考点】38：规律型：图形的变化类．
【分析】结合图形数出前三个图形中三角形的个数，发现规律：后一个图形中三角形的个数总比前一个三角形的个数多4．
【解答】解：第1个图形中一共有1个三角形，
第2个图形中一共有1+4=5个三角形，
第3个图形中一共有1+4+4=9个三角形，
…
第n个图形中三角形的个数是1+4（n﹣1）=4n﹣3，
当n=2017时，4n﹣3=8065，
故答案为：8065．

二、选择题（每题3分，满分30分）
11．下列各运算中，计算正确的是（ ）
A．（x﹣2）2=x2﹣4B．（3a2）3=9a6C．x6÷x2=x3D．x3•x2=x5
【考点】4I：整式的混合运算．
【分析】根据整式的运算法则即可求出答案．
【解答】解：（A）原式=x2﹣4x+4，故A错误；
（B）原式=27a6，故B错误；
（C）原式=x4，故C错误；
故选（D）

12．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
【考点】R5：中心对称图形；P3：轴对称图形．
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．
【解答】解：A、不是轴对称图形，也不是中心对称图形，故本选项错误；
B、不是轴对称图形，也不是中心对称图形，故本选项错误；
C、既是轴对称图形，又是中心对称图形，故本选项正确；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选C．

13．几个相同的小正方体所搭成的几何体的俯视图如图所示，小正方形中的数字表示在该位置小正方体的个数最多是（ ）
俯视图 左视图
A．5个B．7个C．8个D．9个
【考点】U3：由三视图判断几何体．
【分析】根据俯视图知几何体的底层有4个小正方形组成，而左视图是由3个小正方形组成，故这个几何体的后排最有1个小正方体，前排最多有2×3=6个小正方体，即可解答．
【解答】解：由俯视图及左视图知，构成该几何体的小正方形体个数最多的情况如下：
故选：B．

14．一组从小到大排列的数据：a，3，4，4，6（a为正整数），唯一的众数是4，则该组数据的平均数是（ ）
A．3.6B．3.8C．3.6或3.8D．4.2
【考点】W5：众数；W1：算术平均数．
【分析】根据众数的定义得出正整数a的值，再根据平均数的定义求解可得．
【解答】解：∵数据：a，3，4，4，6（a为正整数），唯一的众数是4，
∴a=1或2，
当a=1时，平均数为=3.6；
当a=2时，平均数为=3.8；
故选：C．

15．如图，某工厂有甲、乙两个大小相同的蓄水池，且中间有管道连通，现要向甲池中注水，若单位时间内的注水量不变，那么从注水开始，乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是（ ）
A．B．C．D．
【考点】E6：函数的图象．
【分析】根据特殊点的实际意义即可求出答案．
【解答】解：先注甲速度较快，水到达连接的地方，水面上升比较慢，最后水面持平后继续上升，
故选：D．

16．若关于x的分式方程的解为非负数，则a的取值范围是（ ）
A．a≥1B．a＞1C．a≥1且a≠4D．a＞1且a≠4
【考点】B2：分式方程的解．
【分析】分式方程去分母转化为整式方程，表示出整式方程的解，根据解为非负数及分式方程分母不为0求出a的范围即可．
【解答】解：去分母得：2（2x﹣a）=x﹣2，
解得：x=，
由题意得：≥0且≠2，
解得：a≥1且a≠4，
故选：C．

17．在平行四边形ABCD中，∠A的平分线把BC边分成长度是3和4的两部分，则平行四边形ABCD周长是（ ）
A．22B．20C．22或20D．18
【考点】L5：平行四边形的性质．
【分析】根据AE平分∠BAD及AD∥BC可得出AB=BE，BC=BE+EC，从而根据AB、AD的长可求出平行四边形的周长．
【解答】解：在平行四边形ABCD中，AD∥BC，则∠DAE=∠AEB．
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BAE=∠BEA，
∴AB=BE，BC=BE+EC，
①当BE=3，EC=4时，
平行四边形ABCD的周长为：2（AB+AD）=2（3+3+4）=20．
②当BE=4，EC=3时，
平行四边形ABCD的周长为：2（AB+AD）=2（4+4+3）=22．
故选：C．

18．如图，是反比例函数y1=和一次函数y2=mx+n的图象，若y1＜y2，则相应的x的取值范围是（ ）
A．1＜x＜6B．x＜1C．x＜6D．x＞1
【考点】G8：反比例函数与一次函数的交点问题．
【分析】观察图象得到：当1＜x＜6时，一次函数y2的图象都在反比例函数y1的图象的上方，即满足y1＜y2．
【解答】解：由图形可知：若y1＜y2，则相应的x的取值范围是：1＜x＜6；
故选A．

19．某企业决定投资不超过20万元建造A、B两种类型的温室大棚．经测算，投资A种类型的大棚6万元/个、B种类型的大棚7万元/个，那么建造方案有（ ）
A．2种B．3种C．4种D．5种
【考点】95：二元一次方程的应用．
【分析】直接根据题意假设出未知数，进而得出不等式进而分析得出答案．
【解答】解：设建造A种类型的温室大棚x个，建造B种类型的温室大棚y个，根据题意可得：
6x+7y≤20，
当x=1，y=2符合题意；
当x=2，y=1符合题意；
当x=3，y=0符合题意；
故建造方案有3种．
故选：B．

20．如图，在边长为4的正方形ABCD中，E、F是AD边上的两个动点，且AE=FD，连接BE、CF、BD，CF与BD交于点G，连接AG交BE于点H，连接DH，下列结论正确的个数是（ ）
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG：S△HBG=tan∠DAG ⑤线段DH的最小值是2﹣2．
A．2B．3C．4D．5
【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质；T7：解直角三角形．
【分析】首先证明△ABE≌△DCF，△ADG≌△CDG（SAS），△AGB≌△CGB，利用全等三角形的性质，等高模型、三边关关系一一判断即可．
【解答】解：∵四边形ABCD是正方形，
∴AB=CD，∠BAD=∠ADC=90°，∠ADB=∠CDB=45°，
在△ABE和△DCF中，
，
∴△ABE≌△DCF（SAS），
∴∠ABE=∠DCF，
在△ADG和△CDG中，
，
∴△ADG≌△CDG（SAS），
∴∠DAG=∠DCF，
∴∠ABE=∠DAG，
∵∠DAG+∠BAH=90°，
∴∠BAE+∠BAH=90°，
∴∠AHB=90°，
∴AG⊥BE，故③正确，
同法可证：△AGB≌△CGB，
∵DF∥CB，
∴△CBG∽△FDG，
∴△ABG∽△FDG，故①正确，
∵S△HDG：S△HBG=DG：BG=DF：BC=DF：CD=tan∠FCD，
又∵∠DAG=∠FCD，
∴S△HDG：S△HBG=tan∠FCD，tan∠DAG，故④正确
取AB的中点O，连接OD、OH，
∵正方形的边长为4，
∴AO=OH=×4=2，
由勾股定理得，OD==2，
由三角形的三边关系得，O、D、H三点共线时，DH最小，
DH最小=2﹣2．
无法证明DH平分∠EHG，故②错误，
故①③④⑤正确，
故选C．

三、解答题（满分60分）
21．先化简，再求值：（﹣）÷，请在2，﹣2，0，3当中选一个合适的数代入求值．
【考点】6D：分式的化简求值．
【分析】先化简分式，然后根据分式有意义的条件即可求出m的值，从而可求出原式的值．
【解答】解：原式=（﹣）×
=×﹣×
=﹣
=，
∵m≠±2，0，
∴当m=3时，
原式=3

22．如图，在平面直角坐标系中，Rt△ABC三个顶点都在格点上，点A、B、C的坐标分别为A（﹣1，3），B（﹣3，1），C（﹣1，1）．请解答下列问题：
（1）画出△ABC关于y轴对称的△A1B1C1，并写出B1的坐标．
（2）画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1，并求出点A1走过的路径长．
【考点】R8：作图﹣旋转变换；O4：轨迹；P7：作图﹣轴对称变换．
【分析】（1）根据网格结构找出点A、B、C关于y轴的对称点A1、B1、C1的位置，然后顺次连接即可；
（2）根据弧长公式列式计算即可得解．
【解答】解：（1）如图，B1（3，1）；
（2）如图，A1走过的路径长：×2×π×2=π

23．如图，已知抛物线y=﹣x2+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=﹣x+3交于C、D两点．连接BD、AD．
（1）求m的值．
（2）抛物线上有一点P，满足S△ABP=4S△ABD，求点P的坐标．
【考点】HA：抛物线与x轴的交点；H5：二次函数图象上点的坐标特征．
【分析】（1）利用待定系数法即可解决问题；
（2）利用方程组首先求出点D坐标．由面积关系，推出点P的纵坐标，再利用待定系数法求出点P的坐标即可；
【解答】解：（1）∵抛物线y=﹣x2+mx+3过（3，0），
∴0=﹣9+3m+3，
∴m=2
（2）由，得，，
∴D（，﹣），
∵S△ABP=4S△ABD，
∴AB×|yP|=4×AB×，
∴|yP|=9，yP=±9，
当y=9时，﹣x2+2x+3=9，无实数解，
当y=﹣9时，﹣x2+2x+3=﹣9，x1=1+，x2=1﹣，
∴P（1+，﹣9）或P（1﹣，﹣9）．

24．某校在艺术节选拔节目过程中，从备选的“街舞”、“爵士”、“民族”、“拉丁”四种类型舞蹈中，选择一种学生最喜爱的舞蹈，为此，随机调查了本校的部分学生，并将调查结果绘制成如下统计图表（每位学生只选择一种类型），根据统计图表的信息，解答下列问题：
（1）本次抽样调查的学生人数及a、b的值．
（2）将条形统计图补充完整．
（3）若该校共有1500名学生，试估计全校喜欢“拉丁舞蹈”的学生人数．
【考点】VC：条形统计图；V5：用样本估计总体；VA：统计表．
【分析】（1）由“拉丁”的人数及所占百分比可得总人数，由条形统计图可直接得a、b的值；
（2）由（1）中各种类型舞蹈的人数即可补全条形图；
（3）用样本中“拉丁舞蹈”的百分比乘以总人数可得．
【解答】解：（1）总人数：60÷30%=200（人），a=50÷200=25%，
b=÷200=30%；
（2）如图所示：
（3）1500×30%=450（人）．
答：约有450人喜欢“拉丁舞蹈”．

25．为营造书香家庭，周末小亮和姐姐一起从家出发去图书馆借书，走了6分钟忘带借书证，小亮立即骑路边共享单车返回家中取借书证，姐姐以原来的速度继续向前行走，小亮取到借书证后骑单车原路原速前往图书馆，小亮追上姐姐后用单车带着姐姐一起前往图书馆．已知单车的速度是步行速度的3倍，如图是小亮和姐姐距家的路程y（米）与出发的时间x（分钟）的函数图象，根据图象解答下列问题：
（1）小亮在家停留了 2 分钟．
（2）求小亮骑单车从家出发去图书馆时距家的路程y（米）与出发时间x（分钟）之间的函数关系式．
（3）若小亮和姐姐到图书馆的实际时间为m分钟，原计划步行到达图书馆的时间为n分钟，则n﹣m= 30 分钟．
【考点】FH：一次函数的应用．
【分析】（1）根据路程与速度、时间的关系，首先求出C、B两点的坐标，即可解决问题；
（2）根据C、D两点坐标，利用待定系数法即可解决问题；
（3）求出原计划步行到达图书馆的时间为n，即可解决问题．
【解答】解：（1）步行速度：300÷6=50m/min，单车速度：3×50=150m/min，单车时间：3000÷150=20min，30﹣20=10，
∴C（10，0），
∴A到B是时间==2min，
∴B（8，0），
∴BC=2，
∴小亮在家停留了2分钟．
故答案为2．
（2）设y=kx+b，过C、D（30，3000），
∴，解得，
∴y=150x﹣1500（10≤x≤30）
（3）原计划步行到达图书馆的时间为n分钟，n==60
n﹣m=60﹣30=30分钟，
故答案为30．

26．在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．
旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）
若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．
【考点】LE：正方形的性质；KD：全等三角形的判定与性质；L8：菱形的性质；R2：旋转的性质．
【分析】图2：根据四边形ABCD是正方形，得到AO=OC，BO=OD，AC⊥BD，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，等量代换得到AO=BO，OC′=OD′，∠AOC′=∠BOD′，根据全等三角形的性质得到AC′=BD′，∠OAC′=∠OBD′，于是得到结论；
图3：根据四边形ABCD是菱形，得到AC⊥BD，AO=CO，BO=DO，求得OB=OA，OD=OC，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，求得OD′=OC′，∠AOC′=∠BOD′，根据相似三角形的性质得到BD′=AC′，于是得到结论．
【解答】解：图2结论：AC′=BD′，AC′⊥BD′，
理由：∵四边形ABCD是正方形，
∴AO=OC，BO=OD，AC⊥BD，
∵将Rt△COD旋转得到Rt△C′OD′，
∴OD′=OD，OC′=OC，∠D′OD=∠C′OC，
∴AO=BO，OC′=OD′，∠AOC′=∠BOD′，
在△AOC′与△BOD′中，，
∴△AOC′≌△BOD′，
∴AC′=BD′，∠OAC′=∠OBD′，
∵∠AO′D′=∠BO′O，∠O′BO+∠BO′O=90°，
∴∠O′AC′+∠AO′D′=90°，
∴AC′⊥BD′；
图3结论：BD′=AC′，AC′⊥BD’
理由：∵四边形ABCD是菱形，
∴AC⊥BD，AO=CO，BO=DO，
∵∠ABC=60°，
∴∠ABO=30°，
∴OB=OA，OD=OC，
∵将Rt△COD旋转得到Rt△C′OD′，
∴OD′=OD，OC′=OC，∠D′OD=∠C′OC，
∴OD′=OC′，∠AOC′=∠BOD′，
∴=，
∴△AOC′∽△BOD′，
∴==，∠OAC′=∠OBD′，
∴BD′=AC′，
∵∠AO′D′=∠BO′O，∠O′BO+∠BO′O=90°，
∴∠O′AC′+∠AO′D′=90°，
∴AC′⊥BD′．

27．由于雾霾天气频发，市场上防护口罩出现热销．某药店准备购进一批口罩，已知1个A型口罩和3个B型口罩共需26元；3个A型口罩和2个B型口罩共需29元．
（1）求一个A型口罩和一个B型口罩的售价各是多少元？
（2）药店准备购进这两种型号的口罩共50个，其中A型口罩数量不少于35个，且不多于B型口罩的3倍，有哪几种购买方案，哪种方案最省钱？
【考点】CE：一元一次不等式组的应用；9A：二元一次方程组的应用．
【分析】（1）设一个A型口罩的售价是a元，一个B型口罩的售价是b元，根据：“1个A型口罩和3个B型口罩共需26元；3个A型口罩和2个B型口罩共需29元”列方程组求解即可；
（2）设A型口罩x个，根据“A型口罩数量不少于35个，且不多于B型口罩的3倍”确定x的取值范围，然后得到有关总费用和A型口罩之间的关系得到函数解析式，确定函数的最值即可．
【解答】解：（1）设一个A型口罩的售价是a元，一个B型口罩的售价是b元，依题意有：
，
解得：．
答：一个A型口罩的售价是5元，一个B型口罩的售价是7元．
（2）设A型口罩x个，依题意有：
，
解得35≤x≤37.5，
∵x为整数，
∴x=35，36，37．
方案如下：
设购买口罩需要y元，则y=5x+7（50﹣x）=﹣2x+350，k=﹣2＜0，
∴y随x增大而减小，
∴x=37时，y的值最小．
答：有3种购买方案，其中方案三最省钱．

28．如图，矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上，线段OA、OC的长度满足方程|x﹣15|+=0（OA＞OC），直线y=kx+b分别与x轴、y轴交于M、N两点，将△BCN沿直线BN折叠，点C恰好落在直线MN上的点D处，且tan∠CBD=
（1）求点B的坐标；
（2）求直线BN的解析式；
（3）将直线BN以每秒1个单位长度的速度沿y轴向下平移，求直线BN扫过矩形AOCB的面积S关于运动的时间t（0＜t≤13）的函数关系式．
【考点】FI：一次函数综合题．
【分析】（1）由非负数的性质可求得x、y的值，则可求得B点坐标；
（2）过D作EF⊥OA于点E，交CB于点F，由条件可求得D点坐标，且可求得=，结合DE∥ON，利用平行线分线段成比例可求得OM和ON的长，则可求得N点坐标，利用待定系数法可求得直线BN的解析式；
（3）设直线BN平移后交y轴于点N′，交AB于点B′，当点N′在x轴上方时，可知S即为▱BNN′B′的面积，当N′在y轴的负半轴上时，可用t表示出直线B′N′的解析式，设交x轴于点G，可用t表示出G点坐标，由S=S四边形BNN′B′﹣S△OGN′，可分别得到S与t的函数关系式．
【解答】解：
（1）∵|x﹣15|+=0，
∴x=15，y=13，
∴OA=BC=15，AB=OC=13，
∴B（15，13）；
（2）如图1，过D作EF⊥OA于点E，交CB于点F，
由折叠的性质可知BD=BC=15，∠BDN=∠BCN=90°，
∵tan∠CBD=，
∴=，且BF2+DF2=BD2=152，解得BF=12，DF=9，
∴CF=OE=15﹣12=3，DE=EF﹣DF=13﹣9=4，
∵∠CND+∠CBD=360°﹣90°﹣90°=180°，且∠ONM+∠CND=180°，
∴∠ONM=∠CBD，
∴=，
∵DE∥ON，
∴==，且OE=3，
∴=，解得OM=6，
∴ON=8，即N（0，8），
把N、B的坐标代入y=kx+b可得，解得，
∴直线BN的解析式为y=x+8；
（3）设直线BN平移后交y轴于点N′，交AB于点B′，
当点N′在x轴上方，即0＜t≤8时，如图2，
由题意可知四边形BNN′B′为平行四边形，且NN′=t，
∴S=NN′•OA=15t；
当点N′在y轴负半轴上，即8＜t≤13时，设直线B′N′交x轴于点G，如图3，
∵NN′=t，
∴可设直线B′N′解析式为y=x+8﹣t，
令y=0，可得x=3t﹣24，
∴OG=24，
∵ON=8，NN′=t，
∴ON′=t﹣8，
∴S=S四边形BNN′B′﹣S△OGN′=15t﹣（t﹣8）（3t﹣24）=﹣t2+39t﹣96；
综上可知S与t的函数关系式为S=．

类型
民族
拉丁
爵士
街舞
据点百分比
a
30%
b
15%
类型
民族
拉丁
爵士
街舞
据点百分比
a
30%
b
15%
方案
B型口罩
B型口罩
一
35
15
二
36
14
三
37
13