中职数学高教版（2021·十四五）基础模块 下册6.6 直线与圆的方程应用举例优质课教案设计

这是一份中职数学高教版（2021·十四五）基础模块 下册6.6 直线与圆的方程应用举例优质课教案设计，共2页。

题目
授课
时长
高等教育出版社《数学》
（基础模块下册）
6.6直线与圆的方程应用举例
1课时
选用教材
授课类型
新授课
本课通过数学建模，借助光线反射和台风区域的实际问题，学习解决与直线
方程和圆的方程有关的实际问题，同时帮助学生体会直线和圆的方程在科技和
生产实践等方面的应用.
教学
提示
能用直线方程与圆的方程解决较简单的实际问题，逐步提升数学建模和数
教学
目标
学运算等核心素养.
教学
重点
教学
难点
教学
环节
用数学知识解决实际问题.
建立数学模型，解决实际问题
教师 学生 设计
活动 活动 意图
教学内容
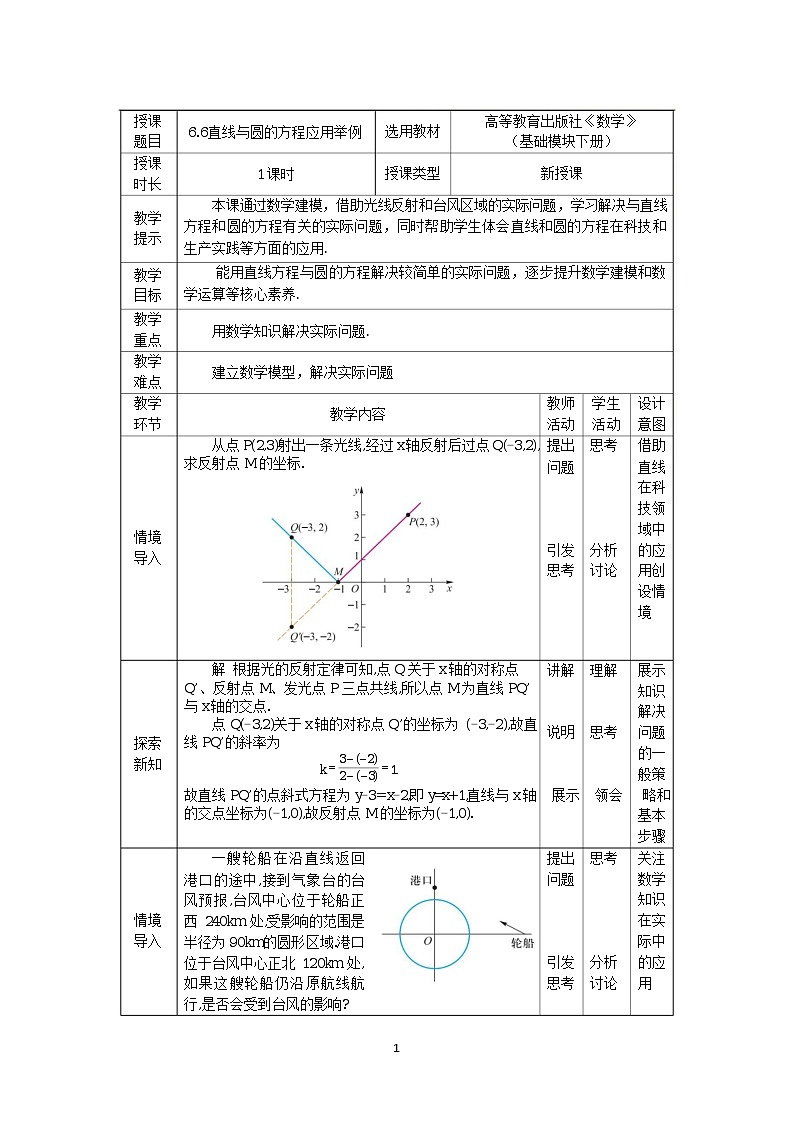
从点 P(2,3)射出一条光线,经过 x轴反射后过点 Q(-3,2), 提出 思考 借助
求反射点 M的坐标.
问题
直线
在科
技领
域中
情境
导入
引发 分析 的应
思考 讨论 用创
设情
境
解 根据光的反射定律可知,点 Q关于 x轴的对称点
Q’、反射点 M、发光点 P三点共线,所以点 M为直线 PQ’
与 x轴的交点.
点 Q(-3,2)关于 x轴的对称点 Q’的坐标为 (-3,-2),故直
线 PQ’的斜率为
讲解 理解 展示
知识
解决
说明 思考 问题
的一
探索
新知
3−(−2)
2−(−3)
k=
=1,
般策
故直线 PQ’的点斜式方程为 y-3=x-2,即 y=x+1,直线与 x轴 展示 领会 略和
的交点坐标为(-1,0),故反射点 M的坐标为(-1,0).
基本
步骤
一艘轮船在沿直线返回
港口的途中,接到气象台的台
风预报,台风中心位于轮船正
西 240km 处,受影响的范围是
半径为 90km的圆形区域.港口
位于台风中心正北 120km 处,
如果这艘轮船仍沿原航线航
行,是否会受到台风的影响?
提出 思考 关注
问题
数学
知识
在实
际中
情境
导入
引发 分析 的应
思考 讨论
用
1

分析 这个实际问题可转化为数学问题:若轮船不改变 讲解 理解 展示
航线,则需考虑轮船航线所在直线与以台风中心为圆心、影
响范围为半径的圆的位置关系,相交或相切会受到影响,相
离则不会受到影响.
知识
解决
说明 思考 问题
解 建立直角坐标系，以台风中心为原点，轮船和台风
中心对应位置的连线为 x轴,以 10km为单位长度.
的一
般策
展示 领会 略和
基本
步骤
探索
新知
设台风中心、轮船、港口对应位置分别为点 O、P、Q，
则它们的坐标分别为 O(0,0)、P(24,0)、Q(0,12).设轮船航线
所在直线 PQ的斜率为 k，则
12− 0
0− 24
1
k=
= − ，
2
由直线的斜截式方程得
1
y=- x+12,即 x+2y-24=0.
2
台风影响的区域是以O(0,0)为圆心,r=9为半径的圆形
区域. 因为圆心 O(0,0)到直线 PQ的距离为
1×0+ 2×0− 24 24
d =
=
> 9，
1
2
+ 22
5
即 d>r,所以轮船航线所在直线与以台风中心为圆心,90km
为半径的圆相离,轮船可沿原航线航行,不会受到台风影响.
练习 6.6
提问 思考 及时
掌握
1.从点 P(1,4)射出一条光线,经过 x轴反射后过点
Q(-4,2),求反射点 M的坐标.
学生
巩固
练习
2.我国的赵州桥是世界上现存年代最久远、跨度最大、
保存最完整单孔坦弧敞肩石拱桥,它的跨度是 37.02m,圆拱
高约 7.2m,求圆拱所在圆的方程.
巡视 动手 掌握
求解 情况
查漏
3.某圆拱桥的跨度是 20m，圆拱高 4m，现有宽 10m的
指导 交流 补缺
船,水面以上高 3m,船能否从桥下通过?
引导 回忆 培养
学生
归纳
总结
提问 反思 总结
学习
过程
能力
说明 记录 继续
1.书面作业：完成课后习题和学习与训练；
2.查漏补缺：根据个人情况对课题学习复习与回顾;
3.拓展作业：阅读教材扩展延伸内容.
布置
作业
探究
延伸
学习
2