江苏省扬州市宝应县氾水镇初级中学2023—2024学年九年级上学期12月月考数学试题

这是一份江苏省扬州市宝应县氾水镇初级中学2023—2024学年九年级上学期12月月考数学试题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 若=，则的值为（ ）
A．1B．C．D．
2.已知☉O的半径为3，若点P在 ☉O 内，则的长可能为( )
A. 2 B. 3C. 4 D. 以上都有可能
3. 将关于x的函数的图像向下平移两个单位，以下说法错误的是( )
A. 开口方向不变 B. 对称轴不变
C. 与y轴交点不变 D. 自变量x的取值范围不变
4.某商品经过连续两次降价，销售单价由原来200元降到162元．设平均每次降价的百分率为x，根据题意可列方程为（ ）
A．200（1﹣x）2＝162B．200（1+x）2＝162
C．162（1+x）2＝200D．162（1﹣x）2＝200
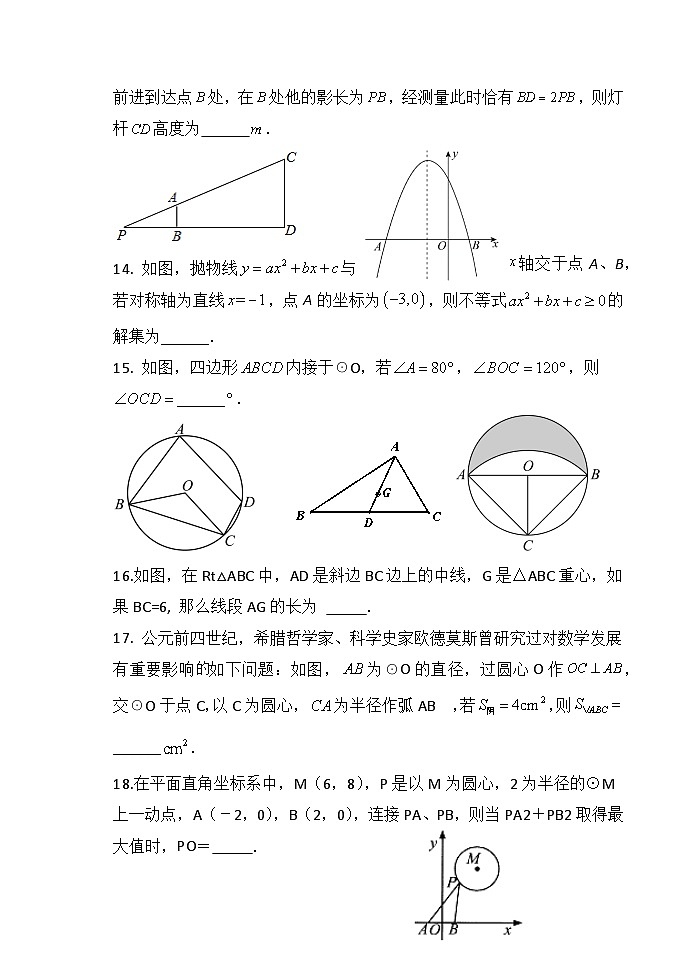
5、如图，已知直线AB是⊙O的切线，A为切点，OB交⊙O于点C，点D在⊙O上，且∠OBA=40°，则∠ADC=( )
40° B、25 ° C、 30° D、35°
6.已知抛物线的图像上三个点的坐标分别为更多课件教案等优质滋元可 家 威杏 MXSJ663 ，，，则，，的大小关系为（ ）
A. B. C. D.
7. 如图，用一张矩形纸片覆盖等边△ABC，且，若边被、三等分，则 △ABC被覆盖（阴影部分）的面积是未被覆盖的面积的( )
A. B. C. D.
8. 如图，在中，，点D、E分别在上，交于F，若，，则的值为( )
A. B. C. D.
二、填空题 （每题3分，共30分）
9.如果，那么锐角的度数为
10.小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分，80分，90分，若依次按照2:3:5的比例确定成绩，则小王的成绩 分.
11.把球放在长方体纸盒内，球的一部分露在盒外，其截面如图，已知EF=CD=80 cm则截面圆的半径为 cm.
12.若一个圆锥的侧面展开图是半径为6cm，圆心角为240°的扇形，则这个圆锥的底面半径长是 cm.
13.如图，某学生身高，在灯光下，他从灯杆底部点处，沿直线前进到达点处，在处他的影长为，经测量此时恰有，则灯杆高度为 ．
14. 如图，抛物线与轴交于点A、B，若对称轴为直线，点A的坐标为，则不等式的解集为______．
15. 如图，四边形内接于☉O，若，，则______．
16.如图，在Rt△ABC中，AD是斜边BC边上的中线，G是△ABC重心，如果BC=6, 那么线段AG的长为 ．
17. 公元前四世纪，希腊哲学家、科学史家欧德莫斯曾研究过对数学发展有重要影响如下问题：如图，为☉O的直径，过圆心O作，交☉O于点C，以C为圆心，为半径作弧AB ，若，则______．
18.在平面直角坐标系中，M（6，8），P是以M为圆心，2为半径的⊙M上一动点，A（－2，0），B（2，0），连接PA、PB，则当PA2＋PB2取得最大值时，PO＝ ．
三、解答题（96分）
19.(本题8分)
解下列方程: (2)计算： cs30°+3tan45°﹣20180
20．（本题8分）为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩记录如表：
（1）经计算甲和乙的平均成绩是8（环），请求出表中的a＝ ；
（2）甲成绩的中位数是 环，乙成绩的众数是 环；
（3）若甲成绩的方差是1.2，请求出乙成绩的方差，判断甲、乙两人谁的成绩更为稳定？
21、（本题8分）张老师积极参加社区抗疫志愿服务工作．根据社区安排，志愿者将被随机分到A组（体温检测）、B组（便民代购）、C组（环境消杀）或D组（统筹协调）．
（1）张老师被分到D组概率是；
（2）王老师也参加了该社区的志愿者队伍，请用画树状图或列表的方法，求出他和张老师被分到同一组的概率是多少？
22.（本题8分）如图，在直角坐标系中，边长为1的小正方形组成的网格中，给出了格点△ABC（顶点为网格线的交点），在给定的网格中，解答下列问题：
（1）以A为位似中心，将△ABC按相似比2：1放大，得到，画出．
（2）以为旋转中心，将顺时针旋转，得到．
①画出；点的坐标为 ；
②边扫过的面积为 ．
23.(本题10分）已知关于x的一元二次方程x2-2x-3m2＝0.
（1）求证:方程总有两个不相等的实数根;
（2）若方程的两个实数根分别为a，β,且a+2β=5，求m的值.
24.（本题10分） 如图，正方形的边长为，点是边上的一个动点（点不与点、重合），连接，过点作交于点．
（1）求证：；
（2）当最大时，求的长．
25.（本题10分）如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i=1：，AB=10米，AE=15米．（i=1：是指坡面的铅直高度BH与水平宽度AH的比）
（1）求点B距水平面AE的高度BH；
（2）求广告牌CD的高度．
（测角器的高度忽略不计，结果精确到0.1米．参考数据：1.414，1.732）
26.( 本题10分) 如图，AB为⊙O直径，E为⊙O上一点，∠EAB的平分线AC 交 ⊙O于C点，过C点作CD⊥A E的延长线于D点，直线CD与射线AB交于P点．
（1）求证：DC为⊙O切线；
（2）若DC=1，AC=，求PB的长．
27．（本题12分）小雨、小华、小星暑假到某超市参加社会实践活动，在活动中他们参加了某种水果的销售工作，已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．
小华：“如果以10元/千克的价格销售，那么每天可售出300千克．”
小雨：“如果以13元/千克的价格销售，那么每天可售出150千克．”
小星：“通过调查验证，我发现每天的销售量y（千克）与销售单价x（元）之间存在一次函数关系．”
（1）求y（千克）与 x（元）（x＞0）之间的函数关系式；
（2）一段时间后，发现这种水果每天的销售量均不低于250千克，则此时该超市销售这种水果每天获取的利润w（元）最大是多少？
（3）为响应政府号召，该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润（a≤2.5）给希望工程．公司通过销售记录发现，当销售单价不超过13元时，每天扣除捐赠后的日销售利润随销售单价x （元）的增大而增大，求a的取值范围．
28.（本题12分）如图，二次函数的图像与轴交于点，与轴交于点，顶点的横坐标为.
（1）求二次函数的表达式及的坐标；
（2）若()是轴上一点，，将点绕着点顺时针方向旋转得到点.当点恰好在该二次函数的图像上时，求的值；
（3）在（2）的条件下，连接.若是该二次函数图像上一点，且，求点的坐标.射击次序（次）
1
2
3
4
5
6
7
8
9
10
甲的成绩（环）
8
9
7
9
8
6
7
a
10
8
乙的成绩（环）
6
7
9
7
9
10
8
7
7
10