数学第十七章 勾股定理17.1 勾股定理学案设计

这是一份数学第十七章 勾股定理17.1 勾股定理学案设计，共24页。学案主要包含了学习目标，学习重点，学习活动，课堂检测等内容，欢迎下载使用。
一、学习目标：
1、了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理；
2、培养学生在实际生活中发现问题、总结规律的意识和能力。
二、学习重点：勾股定理的内容及证明
学习难点：勾股定理的证明
三、学习活动：
活动一：课前预习
1、直角三角形ABC的主要性质是：C=90°（用几何语言描述）
（1）两锐角之间的关系：_________________________；
（2）若B=30°，则B的对边与斜边满足的关系：____________________
2、根据题意，画直角三角形ABC，其中C=90°，并回答问题：
（1）AC=3cm，BC=4cm，用量角器量出斜边AB的长为_________cm；
（2）AC=5cm，AB=13cm，用量角器量出另一直角边BC的长为____________cm。
问题：你是否发现32+42的和与52、52+122的和与132的大小关系？
3、阅读书本P63—65页内容，结合P65探究，完成下表，你能发现正方形A、B、C的关系吗？
由此，我们可以得出什么结论？可猜想：
命题1：如果直角三角形的两直角边长分别为，斜边长为，那么_________________。
活动二、勾股定理的证明
已知：在△ABC中，∠C=90°，∠A、∠B、∠C的对边为、。
求证：。
如图，为4个全等的直角三角形，拼成一个大正方形，试利用面积证明。
你还有什么方法证明吗？
由此，我们可以得出：勾股定理 的内容为___________________________________。
活动三、随堂练习：
1、在Rt△ABC中，∠C=90°，
(1)已知a=3，b=4,则c=________。 ⑵已知a=1, c=2, 则b=_________。
(3)已知c=17,b=8, 则a=________。 ⑷已知a：b=1：2, c=5, 则a=________。
第2题图
S1
S2
S3
2、如图，三个正方形中的两个面积S1=25cm2，S2=144cm2，
则第三个的面积S3=_______
3、已知直角三角形的两边长分别为5和12，求第三边。
活动四、课堂检测：
1、在Rt△ABC，∠C=90°
（1）若，（2），
（3），（4）。
2、在Rt△ABC中，∠C=90°，BC=5cm，AB比AC大2cm，则AB=_______cm，
3、直角三角形中两边长为3cm、4cm，则斜边长为_____________cm，
4、已知：如图，等边△ABC的边长是6cm。
⑴求等边△ABC的高。 ⑵求S△ABC。
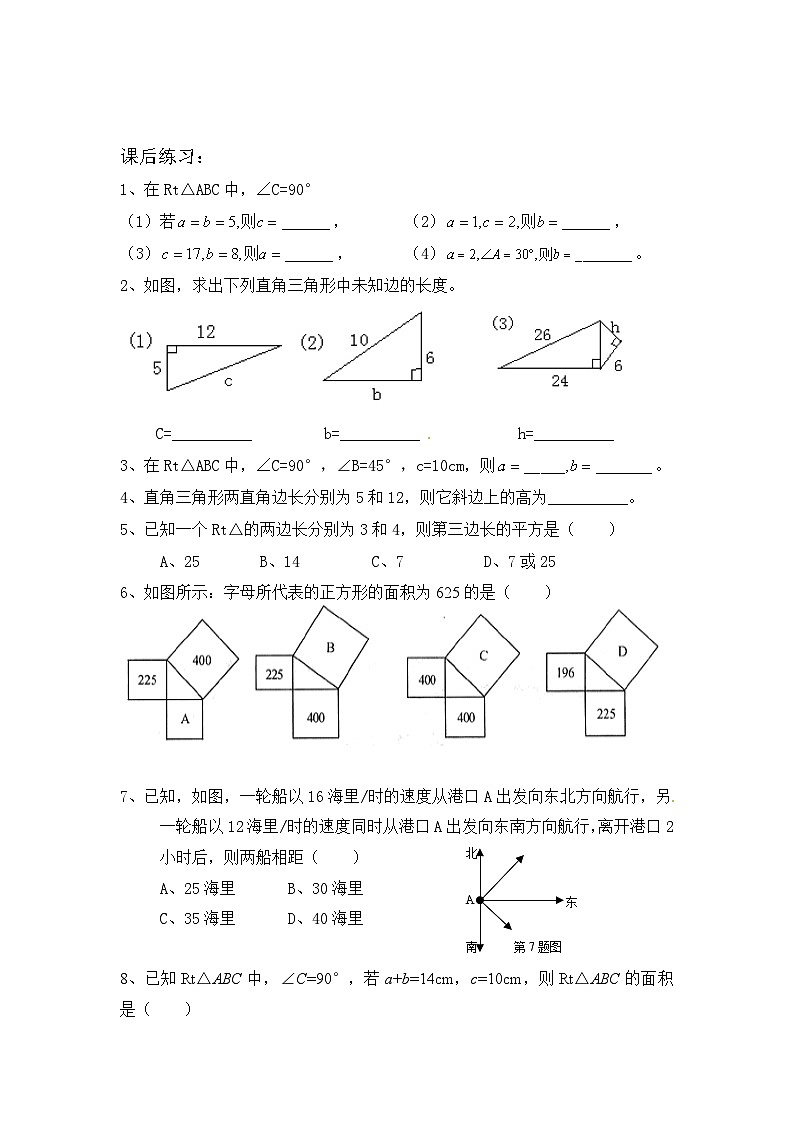
课后练习：
1、在Rt△ABC中，∠C=90°
（1）若，（2），
（3），（4）。
2、如图，求出下列直角三角形中未知边的长度。

C=__________ b=__________ h=__________
3、在Rt△ABC中，∠C=90°，∠B=45°，c=10cm，则。
4、直角三角形两直角边长分别为5和12，则它斜边上的高为__________。
5、已知一个Rt△的两边长分别为3和4，则第三边长的平方是（ ）
A、25B、14C、7D、7或25
6、如图所示：字母所代表的正方形的面积为625的是（ ）
北
南
A
东
第7题图
7、已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（ ）
A、25海里B、30海里
C、35海里D、40海里
8、已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（ ）
A. 24cm2B. 36cm2 C. 48cm2 D. 60cm2
9、如图所示，可以利用两个全等的直角三角形拼出一个梯形．借助这个图形，你能用面积法来验证勾股定理吗？
10、已知在△ABC中，AC=15，BC=20，CD⊥AB于点D，且CD长为9，
试求AB的长。
观河中学八年级数学（下）导学案（二）
课题：勾股定理（二）
一、学习目标：1、会用勾股定理进行简单的运算；
2、树立数形结合的思想、分类讨论的思想。
二、学习重点：勾股定理的简单运用
学习难点：实际问题向数学问题的转化
三、学习活动：
活动一、复习巩固：
例：（1）你能求出下列直角三角形中未知的边吗？．
A
15
C
B
6
10
A
C
B
2
45°
2
30°
（2）归纳：在求解直角三角形的未知边时需要知道哪些条件？应该注意哪些问题？
活动二：应用提高：
探究1 ：
1、在长方形ABCD中，宽AB为1m，长BC为2m ，求AC的长
2、一个门框的尺寸如图所示．
①若有一块长3米，宽0.8米的薄木板，问怎样从门框通过？
②若薄木板长3米，宽1.5米呢？
③若薄木板长3米，宽2.2米呢？为什么？
O
B
D
CＣ
A
探究2 如图，一个3米长的梯子AB，斜着靠在竖直的墙AO上，
这时AO的距离为2.5米．
①球梯子的底端B距墙角O多少米？
②如果梯的顶端A沿墙下滑0.5米至C，请同学们猜一猜，
底端也将滑动0.5米吗？
若不是，请算一算，底端滑动的距离是多少（结果保留两位小数）？
活动三、随堂练习：
书本P68页 1、2
活动四、课堂检测：
1．小明和爸爸妈妈假期去登山，他们沿着45度的坡路走了500米，看到了一棵红叶树，求这棵红叶树的离地面的高度。
2．如图，山坡上两株树木之间的坡面距离AC是10米，则这两株树之间的垂直距离BC和水平距离AB是多少米？
3．如图，一根12米高的电线杆两侧各用15米的铁丝固定，求两个固定点之间的距离。
4．有一个边长为1米正方形的洞口，想用一个圆形盖去盖住这个洞口，则圆形盖半径至少为多少米？
课后练习：
如图，Rt△RPQ中，RP⊥PQ，且PQ=16厘米，RP+RQ=32厘米，则RQ= 厘米。
2、小明想知道学校旗杆的高度，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端沿地面拉开5米时，绳子的下端恰好接触地面，你能帮小明求一求旗杆的高度吗？
3、已知：如图，在四边形ABCD中，AD∥BC，AD⊥CD，AB⊥AC，∠B=60°，CD=1cm，求BC的长。
4、如图是一个圆柱，圆柱的底面圆周长是10cm，圆柱高是6cm，一只蚂蚁沿外壁爬行，要从A点爬到B点，则最少要爬行多少cm?
观河中学八年级（下）数学导学案（三）
课题：勾股定理（三）
一、学习目标：
1、能在数轴上画出表示无理数的点，进一步体会实数与数轴上的点一一对应的关系；
2、会用勾股定理解决较综合的问题。
3、树立数形结合的思想。
二、学习重点：勾股定理的综合应用。
学习难点：勾股定理的综合应用。
三、学习活动：
活动一、复习：
1、勾股定理：___________________________________________。
2、在Rt△ABC中，∠C=90°，根据下列要求填空：
（1）若； （2）；
（3）； （4）
3、结合第2题，你能在数轴上表示、、吗？试试看：
活动二、例题讲解：
例1、利用勾股定理知识，在数轴上作出表示、-的点。类似的，你还能作出哪些无理数表示的点？
例2、已知：在Rt△ABC中，∠C=90°，CD⊥BC于D，∠A=60°，CD=，
求线段AB的长。
例3、已知：如图，△ABC中，AC=4，∠B=45°，∠A=60°，根据条件你可求什么？

例4、已知：如图，∠B=∠D=90°，∠A=60°，AB=4，CD=2。
求：四边形ABCD的面积。
活动三、随堂练习：
1、完成书本P71练习
2、△ABC中，AB=AC=25cm，高AD=20cm,则BC= ，S△ABC= 。
3、已知直角三角形的两边长分别为3cm和5cm，，则第三边长为 。
活动四、课堂检测：
1．如图，点A在数轴上表示的数为x，则x2-3的值为________；
2、如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了 步路（假设2步为1米），却踩伤了花草．
3、等腰△ABC的腰长AB＝10cm，底BC为16cm，则底边上的高为 ，面积为 .
4、△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（ ）
A．42 B．32 C．42 或 32 D．37 或 33
5、已知：如图，△ABC中，AB=26，BC=25，AC=17，
求S△ABC。
课后练习
1．在Rt△ABC中，∠C=90°，CD⊥BC于D，
（1）若∠A=60°，CD=，则AB= cm；
（2）若BC=6cm，AC=8cm，则高CD=________cm；
2、已知直角三角形中30°角所对的直角边长是cm，则另一条直角边的长是（ ）A. 4cm B. cm C. 6cm D. cm
3、在数轴上画出表示－的点。
4、已知：如图，在△ABC中，∠B=30°，∠C=45°，AC=，
求（1）AB的长；（2）S△ABC。
5、已知，如图，在Rt△ABC中，∠C=90°，AD平分∠CAB，CD=1.5，BD=2.5，
试求边AC的长。
观河中学八年级（下）数学导学案（四）
课题：勾股定理的逆定理（一）
一、学习目标：
1、体会勾股定理的逆定理得出过程，掌握勾股定理的逆定理。
2、探究勾股定理的逆定理的证明方法。
3、理解原命题、逆命题、逆定理的概念及关系。
二、学习重点：掌握勾股定理的逆定理内容及证明。
学习难点：勾股定理的逆定理的证明。
三、学习活动：
活动一、课前预习：
1、叙述勾股定理的内容：___________________________________，
用几何语言可表示为：___________________________________。
2、提问：你有什么方法判断一个三角形是直角三角形吗？试写一写：
3、已知△ABC，∠A、∠B、∠C的对边分别为，
根据下列条件，画出对应的三角形：
（1），（2），（3）
问题：以上所画三个三角形的三边满足什么关系？
所得三角形是直角三角形吗？
你能用语言来描述你的发现吗？
活动二、勾股定理的逆定理证明：
命题2：证明：如果三角形的三边长满足，那么这个三角形是直角三角形。
活动三、随堂练习：
1、书本P69页练习1、2
2、说出下列命题的逆命题，这些命题的逆命题成立吗？
⑴同旁内角互补，两条直线平行。
⑵如果两个实数的平方相等，那么两个实数平方相等。
⑶线段垂直平分线上的点到线段两端点的距离相等。
⑷直角三角形中30°角所对的直角边等于斜边的一半。
3、△ABC中∠A、∠B、∠C的对边分别是，下列命题中的假命题是（ ）
A．如果∠C－∠B=∠A，则△ABC是直角三角形。
B．如果，则△ABC是直角三角形，且∠C=90°。
C．△ABC的三边之比是1：1：，则△ABC是直角三角形。
D．如果∠A：∠B：∠C=5：2：3，则△ABC是直角三角形。
4、已知：在△ABC中，∠A、∠B、∠C的对边分别是，分别为下列长度，判断该三角形是否是直角三角形？并指出那一个角是直角？
（1）=，=，=； （2）=5，=7，=9；
（3）=2，=，=； （4）=5，=，=1。
活动四、课堂检测：
1、任何一个命题都有____________，但并不是任何一个定理都有__________。
2、“两直线平行，内错角相等”的逆命题是__________________，它是______命题。
3、一个三角形的三边之比为3︰4︰5，该三角形的形状是__________，
理由：
4、下列四条线段不能组成直角三角形的是（ ）
A．=8，=15，=17 B．=9，=12，=15
C．=，=，= D．：：=2：3：4
5、如图，四边形ABCD中，∠A=90°，AB=3， BC=12，CD=13，DA=4。
求证：△BCD为直角三角形。
课后作业：
1、写出下列命题的逆命题，并判断逆命题是否正确。
⑴如果3＞0，那么2＞0；
⑵如果三角形有一个角小于90°，那么这个三角形是锐角三角形；
⑶如果两个三角形全等，那么它们的对应角相等；
⑷关于某条直线对称的两条线段一定相等。
2、在△ABC中，若2=2－2，则△ABC是 三角形， 是直角；
3、若三角形的三边是 ⑴1、、2； ⑵； ⑶32，42，52 ⑷9，40，41；
⑸（m＋n）2－1，2（m＋n），（m＋n）2＋1；则构成的是直角三角形的有（ ）
A．2个 B．３个 Ｃ．４个 Ｄ．５个
4、已知：在△ABC中，∠A、∠B、∠C的对边分别是、、c，分别为下列长度，判断该三角形是否是直角三角形？并指出那一个角是直角？
⑴=9，=41，=40； ⑵=15，=16，=6；
⑶=2，=，=4； ⑷=5k，=12k，=13k（k＞0）。
5、三角形的三边长分别为、、（都是整数）。
试判断三角形的形状。
观河中学八年级（下）数学导学案（五）
课题：勾股定理的逆定理（二）
一、学习目标：
1．灵活应用勾股定理的逆定理解决实际问题。
2．进一步加深性质定理与判定定理之间关系的认识。
二、学习重点：灵活应用勾股定理的逆定理解决实际问题。
学习难点：灵活应用勾股定理的逆定理解决实际问题。
三、学习活动：
活动一、复习：
1、勾股定理的逆定理：_______________________________________；
2、下列四组线段：①2、3、4；②5、13、12；③3、4、6；④1、、，其中能组成直角三角形的有_______________。
3、在军事和航海上经常要确定方向和位置，从而使用一些数学知识和数学方法。试复习方位图、方位角的相关知识。
活动二、例题讲解：
例1、一根30米长的细绳折成3段，围成一个三角形，其中一条边的长度比较短边长7米，比较长边短1米，请你试判断这个三角形的形状。
例2、某港口位于东西方向的海岸线上。“远航”号、“海天”号轮船同时离开港口，各自沿着一固定的方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里，他们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行，你能知道“海天”号沿哪个方向航行吗？（提示：根据题意画出方位图）
活动三、随堂练习：
1、书本P76页练习3
2、小强在操场上向东走80m后，又走了60m，再走100m回到原地。小强在操场上向东走了80m后，又走60m的方向是 。
3、如图，在操场上竖直立着一根长为2米的测影竿，早晨测得它的影长为4米，中午测得它的影长为1米，则A、B、C三点能否构成直角三角形？为什么？
活动四、课堂检测：
1、一根24米绳子，折成三边为三个连续偶数的三角形，则三边长分别为 ，此三角形的形状为 。
2、如果△ABC的三边a,b,c满足关系式 +（b-18）2+=0，
则△ABC是 _______三角形。
3、判断由线段、、组成的三角形是不是直角三角形：
（1）； （2）．
（3）； （4）；
4、已知在△ABD中，AB=13，BC=10，BC边上的中线AD=12.。求证：AB=AC。
5、如图，小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜，爸爸让小明计算一下土地的面积，以便计算一下产量。小明找了一卷米尺，测得AB=4米，BC=3米，CD=13米，DA=12米，又已知∠B=90°。你能求四边形ABCD的面积吗？
课后作业：
1、如图，E、F分别是正方形ABCD的边BC和CD上的两点，且满足CE=BC，AB=4，点F为边CD的中点。连接AE、AF、EF，试判断△AEF的形状，并说明理由。
2、如图，在我国沿海有一艘不明国籍的轮船进入我国海域，我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截，六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里，乙巡逻艇每小时航行50海里，航向为北偏西40°，问：甲巡逻艇的航向？
观河中学八年级（下）数学导学案（六）
课题：勾股定理的逆定理（三）
一、学习目标：
1、应用勾股定理的逆定理判断一个三角形是否是直角三角形。
2、灵活应用勾股定理及逆定理解综合题。
3、进一步加深性质定理与判定定理之间关系的认识。
二、学习重点：利用勾股定理及逆定理解综合题。
学习难点：利用勾股定理及逆定理解综合题。
三、学习活动：
活动一、复习：勾股定理：________________________________；
勾股定理的逆定理：________________________________________。
活动二、例题讲解：
已知：在△ABC中，∠A、∠B、∠C的对边分别是，
满足。试判断△ABC的形状。
例2、已知：如图，四边形ABCD，AD∥BC，AB=4，BC=6，CD=5，AD=3。
求：四边形ABCD的面积。
活动三、随堂练习：
1、若△ABC的三边a、b、c，满足（a－b）（a2＋b2－c2）=0，则△ABC是（ ）
A．等腰三角形； B．直角三角形；
C．等腰三角形或直角三角形； D．等腰直角三角形。
2、若△ABC的三边a、b、c，满足a：b：c=1：1：，试判断△ABC的形状。
3、在△ABC中，AB=13cm，AC=24cm，中线BD=5cm。求证：△ABC是等腰三角形。
活动四、课堂检测：
1、若△ABC的三边a、b、c满足，求△ABC的面积。
2、若一个三角形三边之比为3︰4︰5，且周长为60cm，求该三角形的面积。
3、已知△ABC中，∠C=90°，∠B=30°，AB边的垂直平分线交BC于点D，垂足为E，BD=4cm。求AC的长。
课后作业：
1、已知△ABC的三边为a、b、c，且a+b=4，ab=1，c=，试判定△ABC的形状。
2、已知：如图，∠1=∠2，AD=AE，D为BC上一点，且BD=DC，AC2=AE2+CE2。
求证：AB2=AE2+CE2。
3、已知：如图，在△ABC中，CD是AB边上的高，且CD2=AD·BD。
求证：△ABC是直角三角形。
4、已知：如图，四边形ABCD，AB=1，BC=，CD=，AD=3，且AB⊥BC。
求：四边形ABCD的面积。
A的面积（单位面积）
B的面积（单位面积）
C的面积（单位面积）
图1
图2