
初中数学人教版八年级下册17.1 勾股定理导学案及答案
展开学习目标1.会用勾股定理进行简单的计算。
2.树立数形结合的思想、分类讨论思想。
3.积极参与,全心投入
学习重点:勾股定理的简单计算。
学习难点:勾股定理的灵活运用。
学习过程:
一、温故知新
1.勾股定理的具体内容是: 。
2.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
⑴两锐角之间的关系: ;
⑵若D为斜边中点,则斜边中线与斜边的关系: ;
⑶若∠B=30°,则∠B的对边和斜边的关系: ;
⑷三边之间的关系: 。
二、学以致用、展示提升
1、在Rt△ABC,∠C=90°
⑴已知a=b=5,求c。
⑵已知a=1,c=2, 求b。
⑶已知c=17,b=8, 求a。
⑷已知a:b=1:2,c=5, 求a。
⑸已知b=15,∠A=30°,求a,c。
2、在Rt△ABC中,有一边是2,另一边是3,则第三边的长是 。
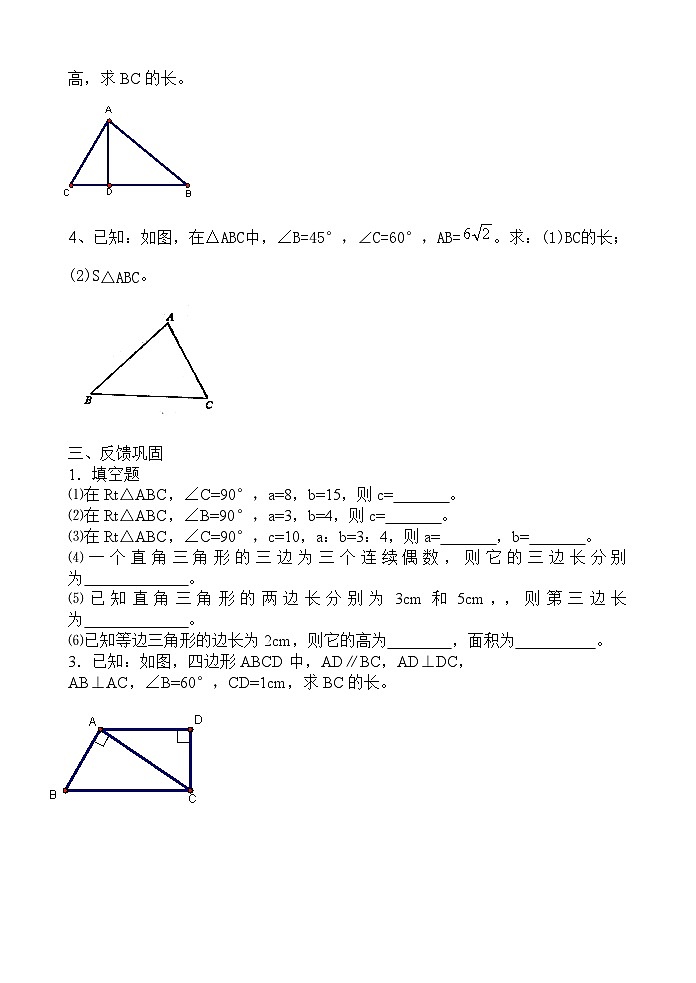
3、已知:如图,在△ABC中,∠C=60°,AB=,AC=4,AD是BC边上的高,求BC的长。
4、已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=。求:(1)BC的长;(2)S△ABC。
三、反馈巩固
1.填空题
⑴在Rt△ABC,∠C=90°,a=8,b=15,则c= 。
⑵在Rt△ABC,∠B=90°,a=3,b=4,则c= 。
⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,则a= ,b= 。
⑷一个直角三角形的三边为三个连续偶数,则它的三边长分别为 。
⑸已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。
⑹已知等边三角形的边长为2cm,则它的高为 ,面积为 。
3.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,
AB⊥AC,∠B=60°,CD=1cm,求BC的长。
勾股定理的应用导学案
班级: 姓名: 评价: 设计:张伟 编号:008
学习目标:1.能用勾股定理解决简单的实际问题。
2.经历将实际问题转化为直角三角形的数学模型过程
3.积极参与,全心投入
学习重点:将实际问题转化为直角三角形模型。
学习难点:如何构建直角三角形,利用勾股定理解决实际问题。
学习过程:
温故知新:
1、判断:若直角三角形的两条边长为6cm、8cm,则第三边长一定为10cm.( )
2、在△ABC中,∠C=90°,若a=5,b=10,则c =
二、探究新知:
活动一:小美妈妈买了一部29英寸(74厘米)的电视机,小美量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,她觉得一定是售货员搞错了。你同意她的想法吗?你能解释这是为什么吗?
活动二:数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的 点吗?
三、学以致用、展示提升
问题一、
大风将一根木制旗杆
吹裂,随时都可能倒下,
十分危急。“110”迅速赶
24米到现场,并决定从断
裂处9米将旗杆折断。现在
需要划出一个安全警戒区域,那
么你能确定这个安全区域的半径至少是多少米吗?
问题二、
一种盛饮料的圆柱形
杯,测得内部底面直径为
5㎝,高为12㎝,吸管放
进杯里,杯口外面露出5㎝,
问吸管要做多长?
问题三、
小东拿着一根长竹竿进
一个宽3米的城门,他先横
着拿进不去,又竖起来拿,
结果竿比城门高1米,当他
把竿斜着时,两端正好顶着
城门的对角,问竿长几米?
问题四:古代问题:
葭生池中
今有方池一丈,
葭生其中央,
出水一尺,
引葭赴岸,
适与岸齐。
问:水深、葭长各几何
四、反馈检测:
1、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
2、利用勾股定理作出长为
的线段.
勾股定理的逆定理(一)导学案
班级: 姓名: 评价: 设计:张伟 编号:009
学习目标
1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2.理解原命题、逆命题、逆定理的概念及关系。
3.阳光参与,做最好的自己。
学习重点:掌握勾股定理的逆定理及简单应用。
学习难点:勾股定理的逆定理的证明。
学习过程:
一.自主预习,探究新知(阅读教材P73 — 75 , 思考下列问题):
1三边长度分别为3 cm、4 cm、5 cm的三角形与以3 cm、4 cm为直角边的直角三角形之间有什么关系?他们全等吗?画图试试
2.你能证明以6cm、8cm、10cm为三边长的三角形是直角三角形吗?
3.什么叫互为逆命题?什么叫互为逆定理?任何一个命题都有 _____,但任何一个定理未必都有 __
4.说出下列命题的逆命题。这些命题的逆命题成立吗?
两直线平行,内错角相等;
逆命题:
如果两个实数相等,那么它们的绝对值相等;
逆命题:
二.学以致用、展示提升
1、判断由线段、、组成的三角形是不是直角三角形:
(1); (2);
2.如果△ABC的三边a,b,c满足关系式 +(b-18)2+=0则△ABC是 _______三角形。
3.若△ABC的三边a、b、c,满足a:b:c=1:1:,试判断△ABC的形状。
4、说出下列命题的逆命题。这些命题的逆命题成立吗?
(1)对顶角相等;
逆命题:
(2)角的内部到角的两边距离相等的点在角的平分线上。
逆命题:
5、“神州七号”飞船上一个零件的形状如下图。已知∠A=90°,按规定这个零件中∠DBC都应该为直角。工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
6、一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为多少米?此三角形的形状为?
三.反馈检测,巩固提高
1.以下列各组数为边长,能组成直角三角形的是( )
A. 8,15,17 B.4,5,6 C.5,8,10 D.7,10,14.
2..若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形; B.直角三角形;
C.等腰三角形或直角三角形; D.等腰直角三角形。
3.如果三条线段长a,b,c满足,这三条线段组成的三角形 (是不是)直角三角形,如果是直角三角形,那么它的斜边是
4、.思考:我们知道3、4、5是一组勾股数,那么3k、4k、5k(k是正整数)也是一组勾股数吗 一般地,如果a、b、c是一组勾股数,那么ak、bk、ck(k是正整数)也是一组勾股数吗
5.“如果a2=b2,则a=b”的逆命题是______________。这个命题_____(填“成立”或“不成立”)。
6、.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90
勾股定理复习
班级: 姓名: 评价: 设计:张伟 编号:010
学习目标
1.熟练应用直角三角形的勾股定理和逆定理来解题.
2.经历反思理解和领会勾股定理和逆定理的过程.
3.激发爱国主义思想,培养良好的学习态度.
学习重点:掌握勾股定理以及逆定理的应用.
学习难点:应用勾股定理以及逆定理.
学习过程:
一、学以致用,系统复习
考点一、已知两边求第三边
1.在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为______.
2.已知直角三角形的两边长为3、2,则另一条边长是________________.
3.在数轴上作出表示的点.
4.已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高.
求 ①AD的长;②ΔABC的面积.
考点二、利用列方程求线段的长
A
D
E
B
C
1.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
2. O
B′
图1
B
A
A′
如图1所示,梯子AB靠在墙上,梯子的底端A到墙根O 的距离为2m,梯子的顶端B到地面的距离为7m.现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离为3m,同时梯子的顶端B下降到B′,那么BB′也等于1m吗?
3.有两棵树,一棵高6米,另一棵高3米,两树相距4米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了___米.
考点三、判别一个三角形是否是直角三角形
1.分别以下列四组数为一个三角形的边长:(1)3、4、5(2)5、12、13(3)8、15、17
(4)4、5、6,其中能够成直角三角形的有
2. 若一个三角形的周长12cm,一边长为3cm,其他两边之差为1cm,则这个三角形是____________
3.在△ABC中,三条边的长分别为a,b,c,a=n2-1,b=2n,c=n2+1(n>1,且n为整数),这个三角形是直角三角形吗?若是,哪个角是直角
考点四、灵活变通
1.在Rt△ABC中, a,b,c分别是三条边,∠B=90°,已知a=6,b=10,则边长c=
2.直角三角形中,以直角边为边长的两个正方形的面积为7,8,则以斜边为边长的正方形的面积为_________.
3.如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬行 cm
4.如图:带阴影部分的半圆的面积是 (取3)
5.一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所爬行的最短路线的长是
6.如图:在一个高6米,长10米的楼梯表面铺地毯,则该地毯的长度至少是 米。
6
8
二、反馈检测
1.在△ABC中,∠C=90°,若 a=5,b=12,则 c=___
2.下列各组线段中,能够组成直角三角形的是( ).
A.6,7,8 B.5,6,7 C.4,5,6 D.3,4,5
3.若等边△ABC的边长为2cm,那么△ABC的面积为( ).
A. cm2 B.2 cm2 C.3 cm2 D.4cm2
4.直角三角形的两直角边分别为5cm,12cm,其中斜边上的高为( )
A.6cm B.8.5cm C.30/13cm D.60/13 cm
5.如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )
图1
A
100
64
A.1倍 B.2倍 C.3倍 D.4倍
6.三个正方形的面积如图1,正方形A的面积为( )
A. 6 B. 36 C. 64 D. 8
7.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是___.
8.如图8,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8m处,已知旗杆原长16m,你能求出旗杆在离底部什么位置断裂的吗?
8m
图8
9.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1m,当它把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为 ( )
A.8cm B.10cm C.12cm D.14cm
10.如图,在四边形ABCD中,∠C=90°,AB=13,BC=4,CD=3,AD=12,求证:AD⊥BD.
11.已知:如图△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
求:BD的长.
人教版17.1 勾股定理导学案: 这是一份人教版17.1 勾股定理导学案,共12页。学案主要包含了学习目标等内容,欢迎下载使用。
初中人教版17.1 勾股定理学案: 这是一份初中人教版17.1 勾股定理学案,共2页。
初中人教版第十七章 勾股定理17.1 勾股定理学案及答案: 这是一份初中人教版第十七章 勾股定理17.1 勾股定理学案及答案,共3页。学案主要包含了针对训练等内容,欢迎下载使用。