




中考数学冲刺复习第七章图形的变换与坐标第34课图形的变换坐标函数课件
展开同一平面直角坐标系中,感受图形变换前后(平移、轴对称、旋转、相似等)点的坐标的变化规律.
【例1】在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA向右平移3个单位长度,得到线段O1A1,则点O1的坐标是__________,A1的坐标是__________.
【考点1】在坐标系中图形变换前后,确定点的位置和坐标
【变式1】如图,在平面直角坐标系xOy中,已知点 A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′, 则点A′的坐标是________.
【考点2】在坐标系中图形变换前后,解决有关 函数的问题
【例2】如图,将△AOB绕点O逆时针旋转90°,得到△A′OB′.(1)若点A的坐标为(a,b),则点A′的坐标为________;(2)若tan∠AOB= ,OB=4,反比例函数y= (k≠0)经过点A′,求k的值.
解:(1)(-b,a) (2)由(1)知A′(-2,4), ∴k的值为-8.
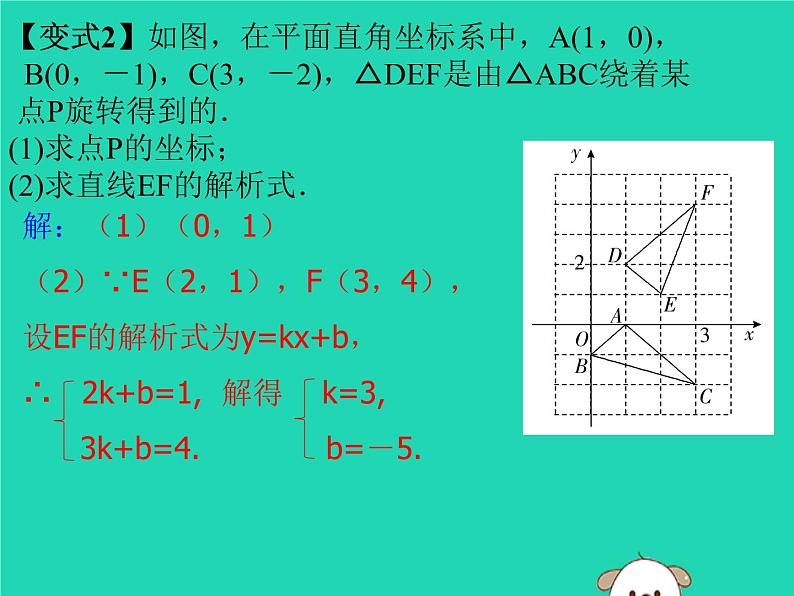
【变式2】如图,在平面直角坐标系中,A(1,0), B(0,-1),C(3,-2),△DEF是由△ABC绕着某 点P旋转得到的.(1)求点P的坐标;(2)求直线EF的解析式.
解:(1)(0,1)(2)∵E(2,1),F(3,4),设EF的解析式为y=kx+b,∴ 2k+b=1, 解得 k=3, 3k+b=4. b=-5.
【考点3】在坐标系中图形变换前后,相似问题
【例3】如图,已知抛物线y=2x2-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)写出以A,B,C为顶点的三角形面积;(2)过点D(m,0)(其中m>1)且与x轴垂直的直线l上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长.(用含m的代数式表示)
解:(1)∵y=2x2-2,∴当y=0时,2x2-2=0,x=±1,∴点A的坐标为(-1,0), 点B的坐标为(1,0),AB=2.又当x=0时,y=-2, ∴点C的坐标为(0,-2),OC=2. ∴S△ABC= AB·OC= ×2×2=2.
【变式3】如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O,若点A的坐标是(1,2),B的坐标是(2,1).(1)求点A′和B′的坐标.(2)过点A的双曲线为 ,过点A′的双曲线为 ,求n-m的值.
解:(1)A′(-2,-4),B′(-4,-2). (2)由已知,得m=2. n=8. ∴n-m=6.
1.如图,方格纸中每个小正方形的边长都是1个单位长度, Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画 出△A1B1C的图形,(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移 后对应的△A2B2C2的图形;(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转 中心的坐标.
解:(1)图略 (2)图略 (3)旋转中心坐标(0,-2)
2.(1)如图,写出坐标系中△ABC与△A′B′C′的顶点坐标,并判断这两个三角形是通过怎样的变换得到的;(2)如果点M(m+1,n-3)与点M′(2m+1,-7+n)是两个三角形中的对应点,求m,n的值.
解:(1)A(2,4),B(-2,2),C(3,1), A′(2,-4),B′(-2,-2),C′(3,-1). 关于x轴对称得到.(2)由题意,得 m+1=2m+1, 解得 n=5, n-3=-(-7+n). m=0
3.如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-2,0),(-1,0),BC⊥x轴,将△ABC沿y轴翻折,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,求点C′的坐标.
解:把A(-2,0)代入y=x+b, 得-2+b=0,b=2. ∴y=x+2, 当x=1时,y=1+2=3, ∴点C′的坐标为 (1,3) .
4.如图,在平面直角坐标系中,△ABC和 △A1B1C1关于点E成中心对称.(1)画出对称中心E,并写出点E,A,C的坐标;(2)P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2,并写出点A2,C2的坐标;(3)判断△A2B2C2和△A1B1C1的位置关系.(直接写出结果)
解:(1)E(-3,-1),A(-3,2), C(-2,0) (2)A2(3,4),C2(4,2). (3)△A2B2C2与△A1B1C1 关于原点O成中心对称.
5.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,(1)求证:①BE=DG;②BE⊥DG;(2)用a和b的代数式表示DE2+BG2.
解:(1)证明:设BE,DG交于点O,∵四边形ABCD和EFGC都为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCD+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG. 在△BCE和△DCG中,∵BC=DC,∠BCE=∠DCG,CE=CG,∴△BCE≌△DCG(SAS).∴BE=DG,∴∠1=∠2. ∵∠BCD=90°∵∠2+∠3=∠1+∠4=90°, ∴∠BOD=90°,∴BE⊥DG.
中考数学冲刺复习第七章图形的变换与坐标第31课轴对称与中心对称课件: 这是一份中考数学冲刺复习第七章图形的变换与坐标第31课轴对称与中心对称课件,共10页。PPT课件主要包含了考点知识,全等的,垂直平分线,对称中心,例题与变式,过关训练等内容,欢迎下载使用。
中考数学冲刺复习第七章图形的变换与坐标第32课平移与旋转课件: 这是一份中考数学冲刺复习第七章图形的变换与坐标第32课平移与旋转课件,共12页。PPT课件主要包含了考点知识,平行且相等,考点1平移的性质,例题与变式,考点2旋转的性质,过关训练等内容,欢迎下载使用。
中考数学冲刺复习第七章图形的变换与坐标第32课平移与旋转课件: 这是一份中考数学冲刺复习第七章图形的变换与坐标第32课平移与旋转课件,共12页。PPT课件主要包含了考点知识,平行且相等,考点1平移的性质,例题与变式,考点2旋转的性质,过关训练等内容,欢迎下载使用。












