

还剩7页未读,
继续阅读
考点05 平抛运动的规律及应用(解析版)—高中物理
展开
这是一份考点05 平抛运动的规律及应用(解析版)—高中物理,共10页。
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在重力作用下的运动.
2.性质:平抛运动是加速度为g的匀变速曲线运动,运动轨迹是抛物线.
3.研究方法:化曲为直
(1)水平方向:匀速直线运动;
(2)竖直方向:自由落体运动.
4.基本规律:
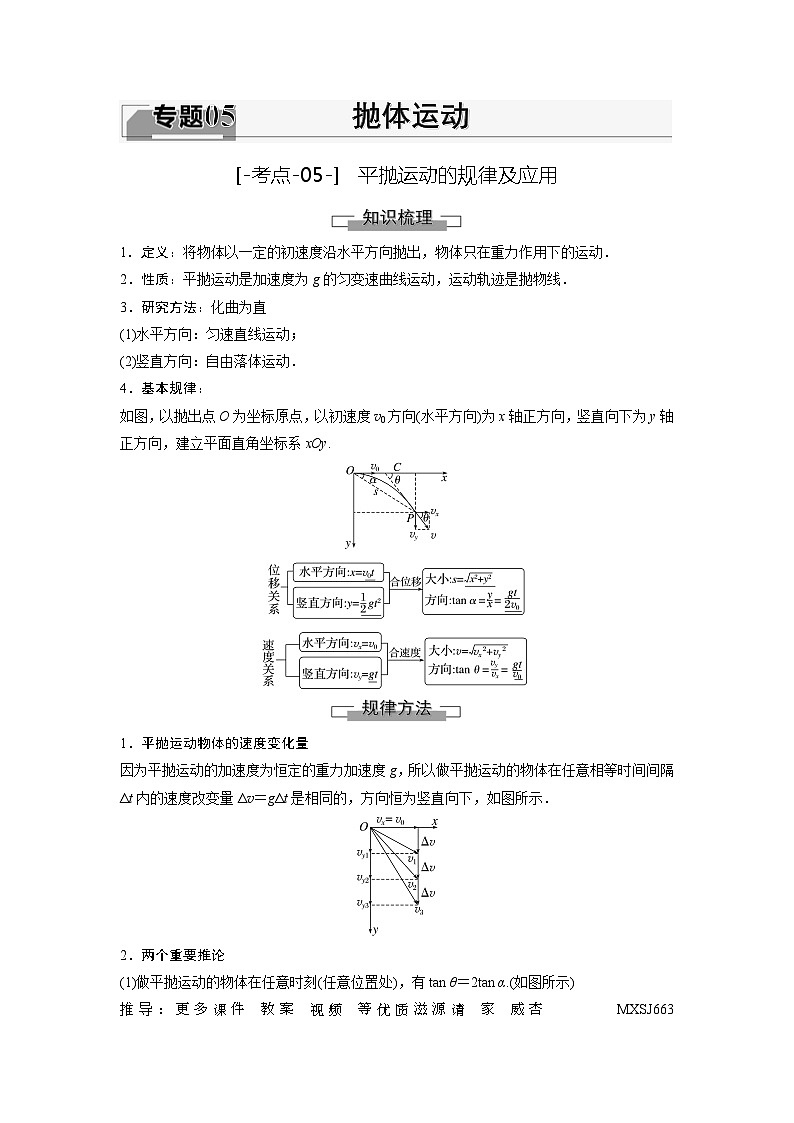
如图,以抛出点O为坐标原点,以初速度v0方向(水平方向)为x轴正方向,竖直向下为y轴正方向,建立平面直角坐标系xOy.
1.平抛运动物体的速度变化量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下,如图所示.
2.两个重要推论
(1)做平抛运动的物体在任意时刻(任意位置处),有tan θ=2tan α.(如图所示)
推导:更多课件 教案 视频 等优质滋源请 家 威杏 MXSJ663 eq \b\lc\ \rc\}(\a\vs4\al\c1(tan θ=\f(vy,v0)=\f(gt,v0),tan α=\f(y,x)=\f(gt,2v0)))→tan θ=2tan α
(2)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过水平位移的中点,如图所示,即xB=eq \f(xA,2).
推导:eq \b\lc\ \rc\}(\a\vs4\al\c1(tan θ=\f(yA,xA-xB),tan θ=\f(vy,v0)=\f(2yA,xA)))→xB=eq \f(xA,2)
典例1(对平抛运动的理解)关于平抛运动,下列说法中不正确的是( )
A.平抛运动的下落时间由下落高度决定
B.平抛运动的轨迹是曲线,所以平抛运动不可能是匀变速运动
C.平抛运动的速度方向与加速度方向的夹角一定越来越小
D.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动
答案 B
解析 平抛运动的下落时间由下落的高度决定,A正确;平抛运动的轨迹是曲线,它的速度方向沿轨迹的切线方向,方向不断改变,所以平抛运动是变速运动,由于其加速度为g,保持不变,所以平抛运动是匀变速曲线运动,B错误;平抛运动的速度方向和加速度方向的夹角θ满足tan θ=eq \f(vx,vy)=eq \f(v0,gt),因为t一直增大,所以tan θ变小,θ变小,C正确;平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,D正确.
典例2(平抛运动规律的应用)(2022·邯郸一中高二学业考试)如图所示,从地面上方某点,将一小球以5 m/s的初速度沿水平方向抛出,小球经过1 s落地.不计空气阻力,g取10 m/s2,则可求出( )
A.小球抛出时离地面的高度是5 m
B.小球从抛出点到落地点的水平位移大小是6 m
C.小球落地时的速度大小是15 m/s
D.小球落地时的速度方向与水平地面成30°角
答案 A
解析 由题意得小球抛出时离地面的高度为h=eq \f(1,2)gt2=5 m,A正确;小球从抛出点到落地点的水平位移大小为x=v0t=5 m,B错误;小球落地时的速度大小为v=eq \r(v02+gt2)=5eq \r(5) m/s,C错误;设小球落地时的速度方向与水平地面夹角为θ,则tan θ=eq \f(gt,v0)=2≠eq \f(\r(3),3)=tan 30°,故θ不等于30°,D错误.
典例3(平抛运动推论的应用)在电视剧里,我们经常看到这样的画面:屋外刺客向屋里投来两支飞镖,落在墙上,如图所示.现设飞镖是从同一位置做平抛运动射出来的,飞镖A与竖直墙壁成53°角,飞镖B与竖直墙壁成37°角,两落点相距为d,则刺客与墙壁的距离为(已知tan 37°=eq \f(3,4),tan 53°=eq \f(4,3))( )
A.eq \f(9,7)d B.2d C.eq \f(24,7)d D.eq \f(12,7)d
答案 C
解析 由平抛运动的推论知,把两飞镖速度反向延长,交点为水平位移中点,如图所示,设水平位移为x,
eq \f(x,2tan 37°)-eq \f(x,2tan 53°)=d . 解得x=eq \f(24,7)d.
1.(多选)a、b两个物体做平抛运动的轨迹如图所示,设它们抛出的初速度分别为va、vb,从抛出至碰到台上的时间分别为ta、tb,则( )
A.va>vb B.va<vb
C.ta>tb D.ta<tb
答案 AD
解析 由题图知,hb>ha,因为h=eq \f(1,2)gt2,所以ta<tb,又因为x=v0t,且xa>xb,所以va>vb,选项A、D正确.
2.(多选)如图所示,从某高度处水平抛出一小球,经过时间t到达地面时,速度与水平方向的夹角为θ,不计空气阻力,重力加速度为g.下列说法正确的是( )
A.小球水平抛出时的初速度大小为eq \f(gt,tan θ)
B.小球在t时间内的位移方向与水平方向的夹角为eq \f(θ,2)
C.若小球初速度增大,则平抛运动的时间变长
D.若小球初速度增大,则θ减小
答案 AD
解析 由tan θ=eq \f(gt,v0)可得小球平抛的初速度大小v0=eq \f(gt,tan θ),A正确;设小球在t时间内的位移方向与水平方向的夹角为α,由tan α=eq \f(h,x)=eq \f(\f(1,2)gt2,v0t)=eq \f(gt,2v0)=eq \f(1,2)tan θ可知,α≠eq \f(θ,2),B错误;小球做平抛运动的时间t=eq \r(\f(2h,g)),与小球初速度无关,C错误;由tan θ=eq \f(gt,v0)可知,v0越大,θ越小,D正确.
3.如图,抛球游戏中,某人将小球水平抛向地面的小桶,结果球落在小桶的前方.不计空气阻力,为了把小球抛进小桶中,则原地再次水平抛球时,他可以( )
A.增大抛出点高度,同时增大初速度
B.减小抛出点高度,同时减小初速度
C.保持抛出点高度不变,增大初速度
D.保持初速度不变,增大抛出点高度
答案 B
解析 设小球平抛运动的初速度为v0,抛出点离桶的高度为h,水平位移为x,根据h=eq \f(1,2)gt2,可得平抛运动的时间为:t=eq \r(\f(2h,g)),则水平位移为:x=v0t=v0eq \r(\f(2h,g)).增大抛出点高度,同时增大初速度,则水平位移x增大,不会抛进小桶中,故A错误.减小抛出点高度,同时减小初速度,则水平位移x减小,可能会抛进小桶中,故B正确.保持抛出点高度不变,增大初速度,则水平位移x增大,不会抛进小桶中,故C错误.保持初速度不变,增大抛出点高度,则水平位移x增大,不会抛进小桶中,D错误.
4.(2022·广东卷·6)如图所示,在竖直平面内,截面为三角形的小积木悬挂在离地足够高处,一玩具枪的枪口与小积木上P点等高且相距为L.当玩具子弹以水平速度v从枪口向P点射出时,小积木恰好由静止释放,子弹从射出至击中积木所用时间为t.不计空气阻力.下列关于子弹的说法正确的是( )
A.将击中P点,t大于eq \f(L,v)
B.将击中P点,t等于eq \f(L,v)
C.将击中P点上方,t大于eq \f(L,v)
D.将击中P点下方,t等于eq \f(L,v)
答案 B
解析 由题意知枪口与P点等高,子弹和小积木在竖直方向上均做自由落体运动,当子弹击中积木时子弹和积木的运动时间相同,根据h=eq \f(1,2)gt2,可知下落高度相同,所以将击中P点;又由于初始状态子弹到P点的水平距离为L,子弹在水平方向上做匀速直线运动,故有t=eq \f(L,v),故选B.
5.将一个物体以10 m/s的速度从5 m的高度水平抛出,落地时它的速度方向与水平地面的夹角为(不计空气阻力,取g=10 m/s2)( )
A.30° B.45° C.60° D.90°
答案 B
解析 物体做平抛运动,落地时竖直分速度vy=eq \r(2gh)=eq \r(2×10×5) m/s=10 m/s,设落地时它的速度方向与水平地面的夹角为α,则tan α=eq \f(vy,v0)=1,得α=45°.故B正确.
6.将一物体以9.8 m/s的初速度水平抛出,经过一段时间后物体的末速度为初速度的eq \r(3)倍,则这段时间是(g取9.8 m/s2)( )
A.eq \r(3) s B.eq \r(2) s C.eq \f(\r(3),3) s D.eq \f(\r(2),2) s
答案 B
解析 已知v=eq \r(3)v0,则竖直方向分速度vy=eq \r(v2-v02)=eq \r(2)v0.又vy=gt,解得t=eq \f(\r(2)v0,g)=eq \f(\r(2)×9.8,9.8) s=eq \r(2) s,故B正确.
7.某人站在平台上平抛一小球,球离手时的速度为v1,落地时的速度为v2,不计空气阻力,能表示出速度矢量的变化过程的是( )
答案 C
解析 小球做平抛运动,加速度恒为g,则速度的变化量Δv=gΔt恒定,方向始终为竖直向下,故选C.
8.如图所示,小球甲从A点水平抛出,小球乙从B点自由释放,两小球先后经过C点时的速度大小相等,速度方向夹角为45°,已知A、C高度差为h,不计空气阻力,由以上条件可知B、A两点高度差为( )
A.eq \f(1,4)h B.eq \f(1,2)h C.h D.2h
答案 C
解析 小球甲做平抛运动,竖直方向上做自由落体运动,从A到C,由h=eq \f(1,2)gt2可得,甲运动的时间为t甲=eq \r(\f(2h,g)),竖直分速度vy=gt甲=eq \r(2gh),据运动的合成与分解可知,甲在C点的速度v甲=eq \f(vy,cs 45°)=2eq \r(gh)=v乙,乙球做自由落体运动,下落高度h′=eq \f(v乙2,2g)=2h,A、B两点高度差为2h-h=h,故C正确,A、B、D错误.
9.(2023·黑龙江省建新高中高三月考)如图所示,将a、b两小球(均可视为质点)以大小为20eq \r(5) m/s的初速度分别从A、B两点先后相差1 s水平相向抛出,a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,且速度方向相互垂直,不计空气阻力,g取10 m/s2,则抛出点A、B间的水平距离是( )
A.85eq \r(5) m B.100 m
C.200 m D.180eq \r(5) m
答案 D
解析 a的运动时间为t,则b的运动时间为t-1 s,eq \f(gt,v0)·eq \f(gt-1 s,v0)=1,解得t=5 s,又因为x=v0t+v0(t-1 s),解得x=180eq \r(5) m,故选D.
10.如图甲所示是网球发球机,某次室内训练时将发球机放在距地面一定的高度,然后向竖直墙面发射网球.假定网球均水平射出,某两次射出的网球碰到墙面时速度与水平方向夹角分别为30°和60°,若不考虑空气阻力,则( )
A.两次发射的初速度大小之比为3∶1
B.碰到墙面前在空中运动时间之比为1∶eq \r(3)
C.下落高度之比为1∶eq \r(3)
D.碰到墙面时速度大小之比为3∶1
答案 B
解析 网球做平抛运动,设网球碰到墙面时速度与水平方向的夹角为θ,由平抛运动的规律可得tan θ=eq \f(vy,v0)=eq \f(gt,v0)①
x=v0t②
由①②得:tan θ=eq \f(gt2,x),则eq \f(t12,t22)=eq \f(tan 30°,tan 60°),eq \f(t1,t2)=eq \f(1,\r(3)),故B正确;eq \f(v01,v02)=eq \f(t2,t1)=eq \f(\r(3),1),故A错误;eq \f(h1,h2)=eq \f(\f(1,2)gt12,\f(1,2)gt22)=eq \f(t12,t22)=eq \f(1,3),故C错误;碰到墙面时速度为v=eq \f(v0,cs θ),故eq \f(v1,v2)=eq \f(v01,v02)·eq \f(cs 60°,cs 30°)=eq \f(1,1),故D错误.
11.(2022·重庆市高一期末)某同学是滑板运动爱好者.如图所示,在某次运动中,该同学从平台末端以速度v0=4 m/s水平飞出,经0.5 s落在水平地面上.忽略空气阻力,该同学和滑板可视为质点,g取10 m/s2.求:
(1)该同学落地点到平台末端的水平距离;
(2)平台离地面的高度.
答案 (1)2 m (2)1.25 m
解析 (1)设该同学落地点到平台末端的水平距离为x,平抛运动水平方向分运动为匀速直线运动,故x=v0t,解得x=2 m.
(2)设平台离地面的高度为h,平抛运动竖直方向分运动为自由落体运动,故h=eq \f(1,2)gt2,解得h=1.25 m.
12.(2021·扬州市高一期末)棒球运动是一项集智慧、勇敢、趣味与协作于一体的集体运动项目,深受青少年喜爱.如图所示,某次投手在A点将球水平抛向捕手,捕手预备在B点接球,击球员预备在C点击球.棒球可看作质点,空气阻力不计.已知:A点离地面1.8 m,C点离地面1.0 m,A、B两点的水平距离为20 m,球抛出后经0.5 s到达B点,g取10 m/s2.求:
(1)棒球抛出后到达C点的时间;
(2)棒球被抛出时的速度大小;
(3)若击球员和捕手均未碰到球,棒球落地时的速度方向.
答案 (1)0.4 s (2)40 m/s (3)速度方向与水平方向的夹角正切值tan θ=eq \f(3,20)
解析 (1)从A到C竖直高度为hAC=1.8 m-1 m=0.8 m
根据hAC=eq \f(1,2)gt2
解得到达C点的时间t=0.4 s.
(2)从A到B,水平方向,根据xAB=v0tAB
解得v0=40 m/s.
(3)棒球从A到落地,竖直方向有2gh=vy2,
解得vy=6 m/s
则棒球落地时的速度方向与水平方向的夹角正切值tan θ=eq \f(vy,v0)=eq \f(3,20).
13.(2021·淮安市高一期末)如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,其平抛运动轨迹的交点为P,则以下说法正确的是( )
A.a、b两球同时落地B.a、b两球落地速度相等
C.a、b两球在P点相遇D.无论两球初速度大小多大,两球总不能相遇
答案 D
解析 a、b两个小球从不同高度同时沿相反方向水平抛出,竖直分运动为自由落体运动,故落地前任意时刻两球高度不同,不可能相遇,b球的高度较小,根据t=eq \r(\f(2h,g))可知b球一定先落地,A、C错误,D正确;由于两球的初速度大小未知,则无法比较两球落地的速度大小,B错误.
14.(2023·绍兴市·高一月考)某物体做平抛运动时,它的速度方向与水平方向的夹角为θ,其正切值tan θ随时间t变化的图像如图所示(g取10 m/s2),则( )
A.第1 s内物体下落的高度为15 m
B.第1 s内物体下落的高度为10 m
C.物体的初速度为5 m/s
D.物体的初速度是10 m/s
答案 D
解析 根据tan θ=eq \f(gt,v0)=eq \f(g,v0)t,对应题图可得eq \f(g,v0)=1,解得v0=10 m/s,D正确,C错误;第1 s内物体下落的高度h=eq \f(1,2)gt2=eq \f(1,2)×10×12 m=5 m,A、B错误.
15.(2023·保山市·期中)如图所示,在我国空军某部一次军事演习中,一架国产轰炸机正在进行投弹训练,轰炸机以200 m/s的恒定速度向竖直峭壁水平飞行,先释放炸弹甲,再飞行5 s后释放炸弹乙,炸弹甲和炸弹乙均击中竖直峭壁上的目标.不计空气阻力,取重力加速度大小g=10 m/s2,则下列说法正确的是( )
A.炸弹甲击中目标5 s后,炸弹乙击中目标
B.炸弹甲和炸弹乙同时击中目标
C.两击中点间的距离为125 m
D.释放炸弹甲时,飞机与峭壁间的水平距离为1 000 m
答案 B
解析 炸弹在水平方向做匀速直线运动,所以两炸弹同时击中目标,A错误,B正确;设乙击中目标的时间为t,则两击中点间的距离为Δs=eq \f(1,2)g(t+5)2-eq \f(1,2)gt2>eq \f(1,2)×10×52 m=125 m,C错误;释放炸弹甲时,飞机与峭壁间的水平距离为s=v0(t+5)>1 000 m,D错误.
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在重力作用下的运动.
2.性质:平抛运动是加速度为g的匀变速曲线运动,运动轨迹是抛物线.
3.研究方法:化曲为直
(1)水平方向:匀速直线运动;
(2)竖直方向:自由落体运动.
4.基本规律:
如图,以抛出点O为坐标原点,以初速度v0方向(水平方向)为x轴正方向,竖直向下为y轴正方向,建立平面直角坐标系xOy.
1.平抛运动物体的速度变化量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下,如图所示.
2.两个重要推论
(1)做平抛运动的物体在任意时刻(任意位置处),有tan θ=2tan α.(如图所示)
推导:更多课件 教案 视频 等优质滋源请 家 威杏 MXSJ663 eq \b\lc\ \rc\}(\a\vs4\al\c1(tan θ=\f(vy,v0)=\f(gt,v0),tan α=\f(y,x)=\f(gt,2v0)))→tan θ=2tan α
(2)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过水平位移的中点,如图所示,即xB=eq \f(xA,2).
推导:eq \b\lc\ \rc\}(\a\vs4\al\c1(tan θ=\f(yA,xA-xB),tan θ=\f(vy,v0)=\f(2yA,xA)))→xB=eq \f(xA,2)
典例1(对平抛运动的理解)关于平抛运动,下列说法中不正确的是( )
A.平抛运动的下落时间由下落高度决定
B.平抛运动的轨迹是曲线,所以平抛运动不可能是匀变速运动
C.平抛运动的速度方向与加速度方向的夹角一定越来越小
D.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动
答案 B
解析 平抛运动的下落时间由下落的高度决定,A正确;平抛运动的轨迹是曲线,它的速度方向沿轨迹的切线方向,方向不断改变,所以平抛运动是变速运动,由于其加速度为g,保持不变,所以平抛运动是匀变速曲线运动,B错误;平抛运动的速度方向和加速度方向的夹角θ满足tan θ=eq \f(vx,vy)=eq \f(v0,gt),因为t一直增大,所以tan θ变小,θ变小,C正确;平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,D正确.
典例2(平抛运动规律的应用)(2022·邯郸一中高二学业考试)如图所示,从地面上方某点,将一小球以5 m/s的初速度沿水平方向抛出,小球经过1 s落地.不计空气阻力,g取10 m/s2,则可求出( )
A.小球抛出时离地面的高度是5 m
B.小球从抛出点到落地点的水平位移大小是6 m
C.小球落地时的速度大小是15 m/s
D.小球落地时的速度方向与水平地面成30°角
答案 A
解析 由题意得小球抛出时离地面的高度为h=eq \f(1,2)gt2=5 m,A正确;小球从抛出点到落地点的水平位移大小为x=v0t=5 m,B错误;小球落地时的速度大小为v=eq \r(v02+gt2)=5eq \r(5) m/s,C错误;设小球落地时的速度方向与水平地面夹角为θ,则tan θ=eq \f(gt,v0)=2≠eq \f(\r(3),3)=tan 30°,故θ不等于30°,D错误.
典例3(平抛运动推论的应用)在电视剧里,我们经常看到这样的画面:屋外刺客向屋里投来两支飞镖,落在墙上,如图所示.现设飞镖是从同一位置做平抛运动射出来的,飞镖A与竖直墙壁成53°角,飞镖B与竖直墙壁成37°角,两落点相距为d,则刺客与墙壁的距离为(已知tan 37°=eq \f(3,4),tan 53°=eq \f(4,3))( )
A.eq \f(9,7)d B.2d C.eq \f(24,7)d D.eq \f(12,7)d
答案 C
解析 由平抛运动的推论知,把两飞镖速度反向延长,交点为水平位移中点,如图所示,设水平位移为x,
eq \f(x,2tan 37°)-eq \f(x,2tan 53°)=d . 解得x=eq \f(24,7)d.
1.(多选)a、b两个物体做平抛运动的轨迹如图所示,设它们抛出的初速度分别为va、vb,从抛出至碰到台上的时间分别为ta、tb,则( )
A.va>vb B.va<vb
C.ta>tb D.ta<tb
答案 AD
解析 由题图知,hb>ha,因为h=eq \f(1,2)gt2,所以ta<tb,又因为x=v0t,且xa>xb,所以va>vb,选项A、D正确.
2.(多选)如图所示,从某高度处水平抛出一小球,经过时间t到达地面时,速度与水平方向的夹角为θ,不计空气阻力,重力加速度为g.下列说法正确的是( )
A.小球水平抛出时的初速度大小为eq \f(gt,tan θ)
B.小球在t时间内的位移方向与水平方向的夹角为eq \f(θ,2)
C.若小球初速度增大,则平抛运动的时间变长
D.若小球初速度增大,则θ减小
答案 AD
解析 由tan θ=eq \f(gt,v0)可得小球平抛的初速度大小v0=eq \f(gt,tan θ),A正确;设小球在t时间内的位移方向与水平方向的夹角为α,由tan α=eq \f(h,x)=eq \f(\f(1,2)gt2,v0t)=eq \f(gt,2v0)=eq \f(1,2)tan θ可知,α≠eq \f(θ,2),B错误;小球做平抛运动的时间t=eq \r(\f(2h,g)),与小球初速度无关,C错误;由tan θ=eq \f(gt,v0)可知,v0越大,θ越小,D正确.
3.如图,抛球游戏中,某人将小球水平抛向地面的小桶,结果球落在小桶的前方.不计空气阻力,为了把小球抛进小桶中,则原地再次水平抛球时,他可以( )
A.增大抛出点高度,同时增大初速度
B.减小抛出点高度,同时减小初速度
C.保持抛出点高度不变,增大初速度
D.保持初速度不变,增大抛出点高度
答案 B
解析 设小球平抛运动的初速度为v0,抛出点离桶的高度为h,水平位移为x,根据h=eq \f(1,2)gt2,可得平抛运动的时间为:t=eq \r(\f(2h,g)),则水平位移为:x=v0t=v0eq \r(\f(2h,g)).增大抛出点高度,同时增大初速度,则水平位移x增大,不会抛进小桶中,故A错误.减小抛出点高度,同时减小初速度,则水平位移x减小,可能会抛进小桶中,故B正确.保持抛出点高度不变,增大初速度,则水平位移x增大,不会抛进小桶中,故C错误.保持初速度不变,增大抛出点高度,则水平位移x增大,不会抛进小桶中,D错误.
4.(2022·广东卷·6)如图所示,在竖直平面内,截面为三角形的小积木悬挂在离地足够高处,一玩具枪的枪口与小积木上P点等高且相距为L.当玩具子弹以水平速度v从枪口向P点射出时,小积木恰好由静止释放,子弹从射出至击中积木所用时间为t.不计空气阻力.下列关于子弹的说法正确的是( )
A.将击中P点,t大于eq \f(L,v)
B.将击中P点,t等于eq \f(L,v)
C.将击中P点上方,t大于eq \f(L,v)
D.将击中P点下方,t等于eq \f(L,v)
答案 B
解析 由题意知枪口与P点等高,子弹和小积木在竖直方向上均做自由落体运动,当子弹击中积木时子弹和积木的运动时间相同,根据h=eq \f(1,2)gt2,可知下落高度相同,所以将击中P点;又由于初始状态子弹到P点的水平距离为L,子弹在水平方向上做匀速直线运动,故有t=eq \f(L,v),故选B.
5.将一个物体以10 m/s的速度从5 m的高度水平抛出,落地时它的速度方向与水平地面的夹角为(不计空气阻力,取g=10 m/s2)( )
A.30° B.45° C.60° D.90°
答案 B
解析 物体做平抛运动,落地时竖直分速度vy=eq \r(2gh)=eq \r(2×10×5) m/s=10 m/s,设落地时它的速度方向与水平地面的夹角为α,则tan α=eq \f(vy,v0)=1,得α=45°.故B正确.
6.将一物体以9.8 m/s的初速度水平抛出,经过一段时间后物体的末速度为初速度的eq \r(3)倍,则这段时间是(g取9.8 m/s2)( )
A.eq \r(3) s B.eq \r(2) s C.eq \f(\r(3),3) s D.eq \f(\r(2),2) s
答案 B
解析 已知v=eq \r(3)v0,则竖直方向分速度vy=eq \r(v2-v02)=eq \r(2)v0.又vy=gt,解得t=eq \f(\r(2)v0,g)=eq \f(\r(2)×9.8,9.8) s=eq \r(2) s,故B正确.
7.某人站在平台上平抛一小球,球离手时的速度为v1,落地时的速度为v2,不计空气阻力,能表示出速度矢量的变化过程的是( )
答案 C
解析 小球做平抛运动,加速度恒为g,则速度的变化量Δv=gΔt恒定,方向始终为竖直向下,故选C.
8.如图所示,小球甲从A点水平抛出,小球乙从B点自由释放,两小球先后经过C点时的速度大小相等,速度方向夹角为45°,已知A、C高度差为h,不计空气阻力,由以上条件可知B、A两点高度差为( )
A.eq \f(1,4)h B.eq \f(1,2)h C.h D.2h
答案 C
解析 小球甲做平抛运动,竖直方向上做自由落体运动,从A到C,由h=eq \f(1,2)gt2可得,甲运动的时间为t甲=eq \r(\f(2h,g)),竖直分速度vy=gt甲=eq \r(2gh),据运动的合成与分解可知,甲在C点的速度v甲=eq \f(vy,cs 45°)=2eq \r(gh)=v乙,乙球做自由落体运动,下落高度h′=eq \f(v乙2,2g)=2h,A、B两点高度差为2h-h=h,故C正确,A、B、D错误.
9.(2023·黑龙江省建新高中高三月考)如图所示,将a、b两小球(均可视为质点)以大小为20eq \r(5) m/s的初速度分别从A、B两点先后相差1 s水平相向抛出,a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,且速度方向相互垂直,不计空气阻力,g取10 m/s2,则抛出点A、B间的水平距离是( )
A.85eq \r(5) m B.100 m
C.200 m D.180eq \r(5) m
答案 D
解析 a的运动时间为t,则b的运动时间为t-1 s,eq \f(gt,v0)·eq \f(gt-1 s,v0)=1,解得t=5 s,又因为x=v0t+v0(t-1 s),解得x=180eq \r(5) m,故选D.
10.如图甲所示是网球发球机,某次室内训练时将发球机放在距地面一定的高度,然后向竖直墙面发射网球.假定网球均水平射出,某两次射出的网球碰到墙面时速度与水平方向夹角分别为30°和60°,若不考虑空气阻力,则( )
A.两次发射的初速度大小之比为3∶1
B.碰到墙面前在空中运动时间之比为1∶eq \r(3)
C.下落高度之比为1∶eq \r(3)
D.碰到墙面时速度大小之比为3∶1
答案 B
解析 网球做平抛运动,设网球碰到墙面时速度与水平方向的夹角为θ,由平抛运动的规律可得tan θ=eq \f(vy,v0)=eq \f(gt,v0)①
x=v0t②
由①②得:tan θ=eq \f(gt2,x),则eq \f(t12,t22)=eq \f(tan 30°,tan 60°),eq \f(t1,t2)=eq \f(1,\r(3)),故B正确;eq \f(v01,v02)=eq \f(t2,t1)=eq \f(\r(3),1),故A错误;eq \f(h1,h2)=eq \f(\f(1,2)gt12,\f(1,2)gt22)=eq \f(t12,t22)=eq \f(1,3),故C错误;碰到墙面时速度为v=eq \f(v0,cs θ),故eq \f(v1,v2)=eq \f(v01,v02)·eq \f(cs 60°,cs 30°)=eq \f(1,1),故D错误.
11.(2022·重庆市高一期末)某同学是滑板运动爱好者.如图所示,在某次运动中,该同学从平台末端以速度v0=4 m/s水平飞出,经0.5 s落在水平地面上.忽略空气阻力,该同学和滑板可视为质点,g取10 m/s2.求:
(1)该同学落地点到平台末端的水平距离;
(2)平台离地面的高度.
答案 (1)2 m (2)1.25 m
解析 (1)设该同学落地点到平台末端的水平距离为x,平抛运动水平方向分运动为匀速直线运动,故x=v0t,解得x=2 m.
(2)设平台离地面的高度为h,平抛运动竖直方向分运动为自由落体运动,故h=eq \f(1,2)gt2,解得h=1.25 m.
12.(2021·扬州市高一期末)棒球运动是一项集智慧、勇敢、趣味与协作于一体的集体运动项目,深受青少年喜爱.如图所示,某次投手在A点将球水平抛向捕手,捕手预备在B点接球,击球员预备在C点击球.棒球可看作质点,空气阻力不计.已知:A点离地面1.8 m,C点离地面1.0 m,A、B两点的水平距离为20 m,球抛出后经0.5 s到达B点,g取10 m/s2.求:
(1)棒球抛出后到达C点的时间;
(2)棒球被抛出时的速度大小;
(3)若击球员和捕手均未碰到球,棒球落地时的速度方向.
答案 (1)0.4 s (2)40 m/s (3)速度方向与水平方向的夹角正切值tan θ=eq \f(3,20)
解析 (1)从A到C竖直高度为hAC=1.8 m-1 m=0.8 m
根据hAC=eq \f(1,2)gt2
解得到达C点的时间t=0.4 s.
(2)从A到B,水平方向,根据xAB=v0tAB
解得v0=40 m/s.
(3)棒球从A到落地,竖直方向有2gh=vy2,
解得vy=6 m/s
则棒球落地时的速度方向与水平方向的夹角正切值tan θ=eq \f(vy,v0)=eq \f(3,20).
13.(2021·淮安市高一期末)如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,其平抛运动轨迹的交点为P,则以下说法正确的是( )
A.a、b两球同时落地B.a、b两球落地速度相等
C.a、b两球在P点相遇D.无论两球初速度大小多大,两球总不能相遇
答案 D
解析 a、b两个小球从不同高度同时沿相反方向水平抛出,竖直分运动为自由落体运动,故落地前任意时刻两球高度不同,不可能相遇,b球的高度较小,根据t=eq \r(\f(2h,g))可知b球一定先落地,A、C错误,D正确;由于两球的初速度大小未知,则无法比较两球落地的速度大小,B错误.
14.(2023·绍兴市·高一月考)某物体做平抛运动时,它的速度方向与水平方向的夹角为θ,其正切值tan θ随时间t变化的图像如图所示(g取10 m/s2),则( )
A.第1 s内物体下落的高度为15 m
B.第1 s内物体下落的高度为10 m
C.物体的初速度为5 m/s
D.物体的初速度是10 m/s
答案 D
解析 根据tan θ=eq \f(gt,v0)=eq \f(g,v0)t,对应题图可得eq \f(g,v0)=1,解得v0=10 m/s,D正确,C错误;第1 s内物体下落的高度h=eq \f(1,2)gt2=eq \f(1,2)×10×12 m=5 m,A、B错误.
15.(2023·保山市·期中)如图所示,在我国空军某部一次军事演习中,一架国产轰炸机正在进行投弹训练,轰炸机以200 m/s的恒定速度向竖直峭壁水平飞行,先释放炸弹甲,再飞行5 s后释放炸弹乙,炸弹甲和炸弹乙均击中竖直峭壁上的目标.不计空气阻力,取重力加速度大小g=10 m/s2,则下列说法正确的是( )
A.炸弹甲击中目标5 s后,炸弹乙击中目标
B.炸弹甲和炸弹乙同时击中目标
C.两击中点间的距离为125 m
D.释放炸弹甲时,飞机与峭壁间的水平距离为1 000 m
答案 B
解析 炸弹在水平方向做匀速直线运动,所以两炸弹同时击中目标,A错误,B正确;设乙击中目标的时间为t,则两击中点间的距离为Δs=eq \f(1,2)g(t+5)2-eq \f(1,2)gt2>eq \f(1,2)×10×52 m=125 m,C错误;释放炸弹甲时,飞机与峭壁间的水平距离为s=v0(t+5)>1 000 m,D错误.
相关试卷
考点05 宇宙速度(解析版)—高中物理: 这是一份考点05 宇宙速度(解析版)—高中物理,共8页。
考点05 斜面上的圆周运动的临界问题(解析版)—高中物理: 这是一份考点05 斜面上的圆周运动的临界问题(解析版)—高中物理,共12页。
考点05 力的合成(解析版)—高中物理: 这是一份考点05 力的合成(解析版)—高中物理,共10页。