

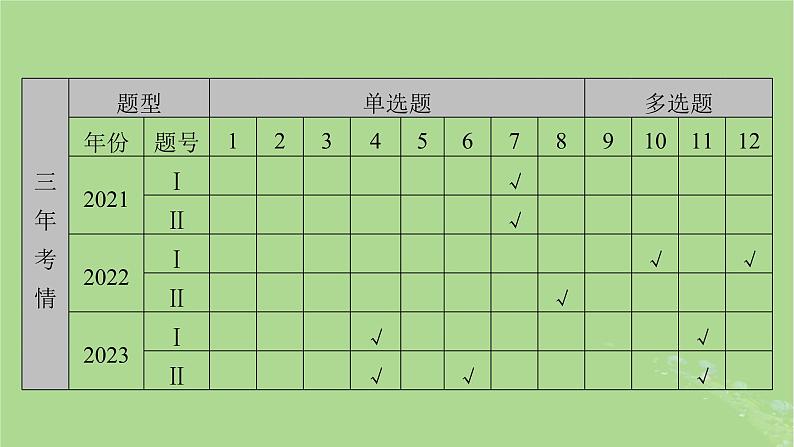
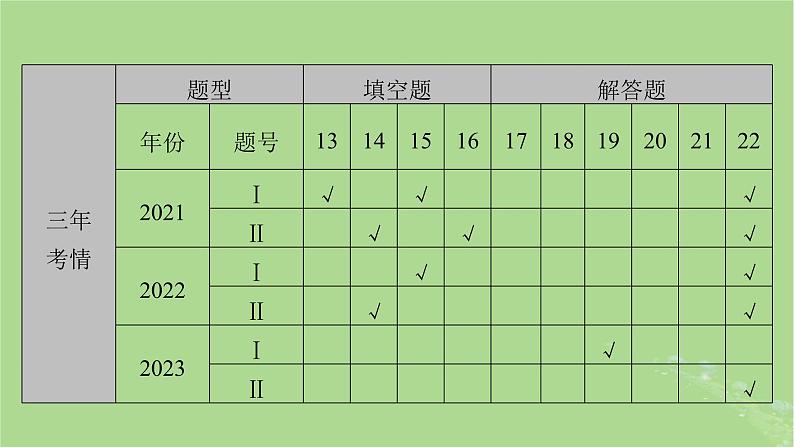



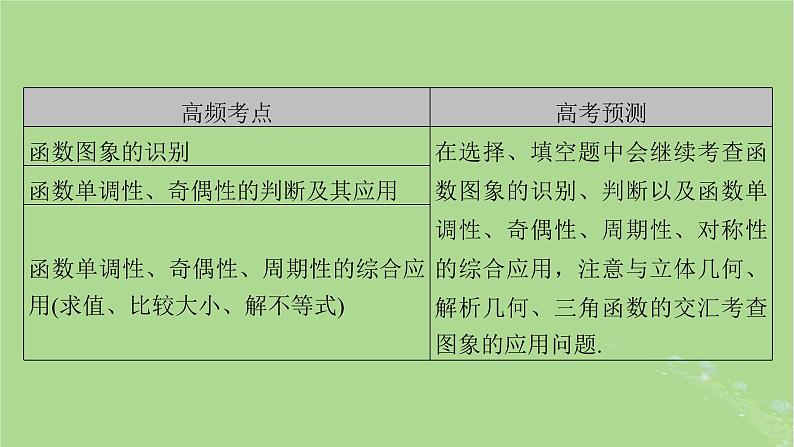
所属成套资源:新教材适用2024版高考数学二轮总复习课件(39份)
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数第3讲导数的简单应用课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题2数列微专题数列与传统文化创新应用课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数第4讲利用导数研究不等式课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数第2讲基本初等函数函数与方程课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数第5讲利用导数研究函数的零点问题课件 课件 0 次下载
新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数第1讲函数的图象与性质课件
展开
这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数第1讲函数的图象与性质课件,共60页。PPT课件主要包含了专题三函数与导数,分析考情·明方向,真题研究·悟高考,考点突破·提能力等内容,欢迎下载使用。
第1讲 函数的图象与性质
A.f(x-1)-1 B.f(x-1)+1C.f(x+1)-1 D.f(x+1)+1
A.-3 B.-2 C.0 D.1
5. (多选)(2023·全国新课标Ⅰ卷)已知函数f(x)的定义域为R,f(xy)=y2f(x)+x2f(y),则( )A.f(0)=0B.f(1)=0C.f(x)是偶函数D.x=0为f(x)的极小值点【解析】 解法一:因为f(xy)=y2f(x)+x2f(y),对于A,令x=y=0,f(0)=0f(0)+0f(0)=0,故A正确.对于B,令x=y=1,f(1)=1f(1)+1f(1),则f(1)=0,故B正确.对于C,令x=y=-1,f(1)=f(-1)+f(-1)=2f(-1),则f(-1)=0,令y=-1,f(-x)=f(x)+x2f(-1)=f(x),又函数f(x)的定义域为R,所以f(x)为偶函数,故C正确.对于D,不妨令f(x)=0,显然符合题设条件,此时f(x)无极值,故D错误.
核心考点1 函数的概念与表示
1.求函数的定义域时要注意三式:分式、根式、对数式,分式中的分母不能为零,偶次根式的被开方数非负,对数的真数大于零.2.复合函数的定义域(1)若f(x)的定义域为[m,n],则在f(g(x))中,m≤g(x)≤n,从中解得x的范围即为f(g(x))的定义域.(2)若f(g(x))的定义域为[m,n],则由m≤x≤n确定的g(x)的范围即为f(x)的定义域.
3.分段函数分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数值域的并集.
角度1:函数的定义域A.[1,5] B.(1,2)∪(2,5)C.(1,2)∪(2,3] D.[1,2)∪(2,3]
角度2:分段函数及其应用A.1 B.2 C.3 D.4
A.(-1,1) B.(-1,+∞)C.{x|x>0或x1或xa B.a>b>cC.b>a>c D.c>a>b
角度2:函数的奇偶性与周期性
5. (2023·洛阳模拟)已知定义在R上的函数f(x)满足f(x)+f(-x)=0,f(-x-1)=f(-x+1),当x∈(0,1)时,f(x)=4x-3,则f(lg480)=( )
角度3:函数基本性质的综合6. (2023·林芝市二模)已知定义在R上的函数f(x)在(-∞,2]上单调递减,且f(x+2)为偶函数,则不等式f(x-1)>f(2x)的解集为( )
7. (2023·九江三模)已知定义在R上的函数f(x)在[0,1]上单调递增,f(x+1)是奇函数,f(x-1)的图象关于直线x=1对称,则f(x)( )A.在[2 020,2 022]上单调递减B.在[2 021,2 023]上单调递增C.在[2 022,2 024]上单调递减D.在[2 023,2 025]上单调递增
【解析】 ∵f(x+1)是奇函数,∴f(x+1)=-f(-x+1),即f(x)的图象关于点(1,0)对称,又∵f(x)在[0,1]上单调递增,∴f(x)在[1,2]上单调递增,即f(x)在[0,2]上单调递增.由f(x+1)=-f(-x+1),可得f(2-x)= -f(x),由f(x-1)图象关于直线x=1对称可知f(x)为偶函数,∴f(x)在[2,4]上单调递减,∴f(2-x)=f(x-2)=-f(x),∴f(x+4)=f(x),∴f(x)是周期函数,最小正周期为4,∵2 022=4×505+2,2 024=4×505+4,∴f(x)在[2 022,2 024]上的单调性和在[2,4]上的单调性相同,∴f(x)在[2 022,2 024]上单调递减.故选C.
1.函数单调性应用问题的常见类型和解题策略(1)比较函数值的大小,应将自变量转化到同一个单调区间,然后利用函数单调性解决;(2)在求解抽象函数有关的不等式时,往往是利用函数的单调性将“f”脱掉,将其转化为具体的不等式求解,此时应特别注意函数的定义域;(3)利用单调性求解最值问题,应先确定函数的单调性,然后再由单调性求解;
(4)利用单调性求参数时,通常把参数视为已知数,根据函数的图象和单调性定义,确定函数的单调区间,将其转化到同一单调区间比较求参数.2.利用奇偶性及周期性的解题策略利用函数奇偶性求值,先利用奇偶性将所求的函数值的自变量转化到已知解析式的函数定义域内,代入解析式即可求出函数值.当函数既具有奇偶性又具有对称性时,先利用奇偶性和对称性确定函数的周期,再利用奇偶性和周期性进行变换,将所求得函数值的自变量转化到已知函数的定义域内求解.
A.(0,4] B.[2,4]C.[2,+∞) D.[4,+∞)
A.函数y=F(x)是奇函数也是周期函数B.函数y=F(x)的最大值为1C.函数y=F(x)在区间(2 022,2 023)上单调递减D.函数y=F(x)的图象有对称中心也有对称轴
相关课件
这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第1讲概率课件,共60页。PPT课件主要包含了专题六概率与统计,第1讲概率,分析考情·明方向,真题研究·悟高考,考点突破·提能力等内容,欢迎下载使用。
这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数微专题常用构造函数的几种方法课件,共25页。PPT课件主要包含了专题三函数与导数,0+∞,-e-3等内容,欢迎下载使用。
这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题3函数与导数第5讲利用导数研究函数的零点问题课件,共51页。PPT课件主要包含了专题三函数与导数,分析考情·明方向,真题研究·悟高考,考点突破·提能力等内容,欢迎下载使用。









