





- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题5解析几何微专题解析几何问题的方法技巧课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第2讲随机变量及其分布列课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计微专题概率与统计的创新问题课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第3讲统计与成对数据的分析课件 课件 0 次下载
- 新教材适用2024版高考数学二轮总复习第2篇核心素养谋局思想方法导航第2讲数形结合思想课件 课件 0 次下载
新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第1讲概率课件
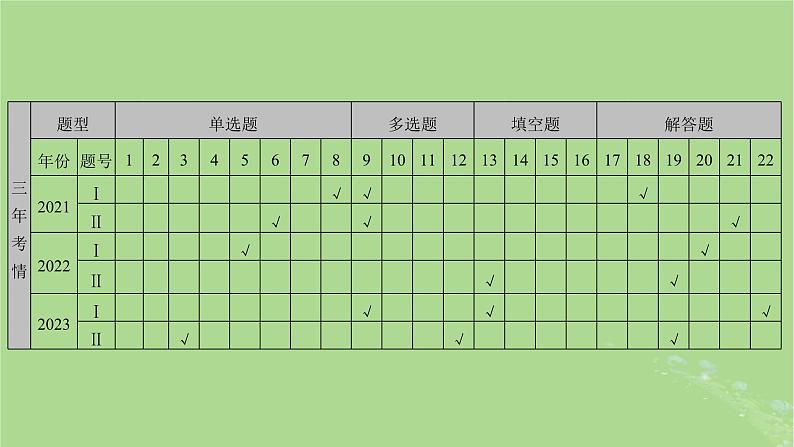
展开3. (2023·全国甲卷理科)有50人报名足球俱乐部,60人报名乒乓球俱乐部,70人报名足球或乒乓球俱乐部,若已知某人报足球俱乐部,则其报乒乓球俱乐部的概率为( )A.0.8B.0.4 C.0.2D.0.1
6. (多选)(2023·全国新高考Ⅱ卷)在信道内传输0,1信号,信号的传输相互独立.发送0时,收到1的概率为α(0<α<1),收到0的概率为1-α;发送1时,收到0的概率为β(0<β<1),收到1的概率为1-β.考虑两种传输方案:单次传输和三次传输.单次传输是指每个信号只发送1次,三次传输是指每个信号重复发送3次.收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1)( )
A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为(1-α)(1-β)2B.采用三次传输方案,若发送1,则依次收到1,0,1的概率为β(1-β)2C.采用三次传输方案,若发送1,则译码为1的概率为β(1-β)2+(1-β)3D.当0<α<0.5时,若发送0,则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率
7. (2022·全国甲卷)从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为______.
8. (2022·全国乙卷)从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为______.
9. (2022·全国新高考Ⅱ卷)已知随机变量X服从正态分布N(2,σ2),且P(2
1.概率的性质性质1:对任意的事件A,都有P(A)≥0;性质2:必然事件的概率为1,不可能事件的概率为0,即P(Ω)=1,P(∅)=0;性质3:如果事件A与事件B互斥,那么P(A∪B)=_____________;
性质4:如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=_______________;性质5:如果A⊆B,那么P(A)≤P(B),由该性质可得,对于任意事件A,因为∅⊆A⊆Ω,所以0≤P(A)≤1;性质6:设A,B是一个随机试验中的两个事件,有P(A∪B)=___________________________________.
P(A)+P(B)-P(A∩B)
角度1:随机事件的关系1. (2023·柳州模拟)从数学必修一、二和政治必修一、二共四本书中任取两本书,那么互斥而不对立的两个事件是( )A.至少有一本政治与都是数学B.至少有一本政治与都是政治C.至少有一本政治与至少有一本数学D.恰有1本政治与恰有2本政治
【解析】 从数学必修一、二和政治必修一、二共四本书中任取两本书,至少有一本政治和都是数学是对立事件,故A错误;至少有一本是政治与都是政治,能同时发生,不是互斥事件,故B错误;至少有一本政治与至少有一本数学,能同时发生,不是互斥事件,故C错误;恰有1本政治与恰有2本政治,不能同时发生,能同时不发生,是互斥而不对立的两个事件,故D正确.故选D.
2. (2023·徐汇区校级三模)某小组有1名男生和2名女生,从中任选2名学生参加围棋比赛,事件“至少有1名男生”与事件“至少有1名女生”( )A.是对立事件B.都是不可能事件C.是互斥事件但不是对立事件D.不是互斥事件【解析】 事件“至少有1名男生”与事件“至少有1名女生”能同时发生,即两名学生正好一名男生,一名女生,故两事件既不是对立事件也不是互斥事件.故选D.
古典概型中样本点个数的探求方法1.列举法:适合的样本点个数较少且易一一列举的问题;2.树状图法:适用于较为复杂的问题中样本点个数的探究,尤其是有序问题;3.排列、组合法:在求解一些较为复杂的问题时,可利用排列、组合知识求出样本点个数.
1. (2023·宜宾模拟)抛掷一枚质地均匀的骰子一次,事件1表示“骰子向上的点数为奇数”,事件2表示“骰子向上的点数为偶数”,事件3表示“骰子向上的点数大于3”,事件4表示“骰子向上的点数小于3”则( )A.事件1与事件3互斥B.事件1与事件2互为对立事件C.事件2与事件3互斥D.事件3与事件4互为对立事件
【解析】 由题意可得事件1表示{1,3,5},事件2表示{2,4,6},事件3表示{4,5,6},事件4表示{1,2},所以事件1与事件2为对立事件,事件1与事件3不互斥,事件2与事件3不互斥,事件3与事件4互斥不对立,故选项A,C,D错误,选项B正确.故选B.
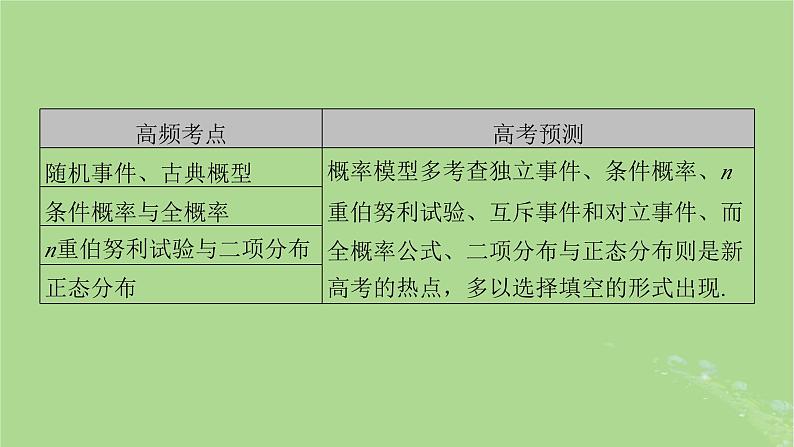
核心考点2 相互独立事件的概率、正态分布
1.概率的几个性质(1)如果A⊆B,则P(A)≤P(B);(2)设A,B是一个随机试验中的两个事件,则P(A∪B)=P(A)+P(B)-P(A∩B).2.正态分布①P(μ-σ≤X≤μ+σ)≈________________;②P(μ-2σ≤X≤μ+2σ)≈________________;③P(μ-3σ≤X≤μ+3σ)≈________________.
0.682 70.954 50.997 3
进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数超过60次的概率为( )(附:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)A.0.158 7B.0.022 8C.0.002 7D.0.001 4
1.利用相互独立事件求复杂事件概率的解题思路(1)将待求复杂事件转化为几个彼此互斥简单事件的和.(2)将彼此互斥简单事件中的简单事件,转化为几个已知(易求)概率的相互独立事件的积事件.(3)代入概率的积、和公式求解.2.利用正态密度曲线的对称性研究概率问题正态密度曲线关于x=μ对称,正态密度曲线与x轴之间的面积为1,注意下面两个结论的活用:(1)P(X
【解析】 甲、乙两人进行象棋比赛,甲胜乙的概率为0.5,乙胜甲的概率为0.3,甲、乙两人平局的概率为0.2.甲、乙两人比赛两局,且两局比赛的结果互不影响,由乙至少赢甲一局是指两局比赛中乙两局全胜或第一局乙胜第二局乙不胜,或第一局乙不胜第二局中乙胜,乙至少赢甲一局的概率为:P=0.3×0.3+0.3×0.7+0.7×0.3=0.51.故选C.
2. (2023·江西模拟)某地市在2023年全市一模测试中,全市高三学生数学成绩X服从正态分布N(90,σ2),已知P(88
P(B|A)+P(C|A)
(3)概率的乘法公式由条件概率的定义知,若P(A)>0,则P(AB)=_________________,我们称该式为概率的乘法公式.
角度2:全概率公式3. (2023·东城区校级模拟)市场上有甲、乙、丙三家工厂生产的同一品牌产品,已知三家工厂的市场占有率分别为30%,20%,50%,且三家工厂的次品率分别为3%,3%,1%,则市场上该品牌产品的次品率为( )A.0.01B.0.02 C.0.03D.0.05
【解析】 设A1,A2,A3分别表示买到一件甲、乙、丙的产品;B表示买到一件次品,由题意有P(A1)=0.3,P(A2)=0.2,P(A3)=0.5,P(B|A1)=0.03,P(B|A2)=0.03,P(B|A3)=0.01,所以P(B)=P(A1)·P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)=0.3×0.03+0.2×0.03+0.5×0.01=0.02.故选B.
1.求条件概率的常用方法
2.全概率公式的实质为了求复杂事件的概率,往往可以把它分解成若干个互斥的简单事件之和,然后利用条件概率和乘法公式,求出这些简单事件的概率,最后利用概率可加,得到最终的结果.3.全概率公式的应用通常把A1,A2,…,An看成导致B发生的一组原因,如若B是“次品”,必是n个车间生产的次品;若B是“某种疾病”,必是几种病因导致B发生;若B表示“被击中”,必有几种方式或几个人打中.
新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第3讲统计与成对数据的分析课件: 这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第3讲统计与成对数据的分析课件,共60页。PPT课件主要包含了专题六概率与统计,分析考情·明方向,真题研究·悟高考,考点突破·提能力,核心考点1抽样方法等内容,欢迎下载使用。
新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计微专题概率与统计的创新问题课件: 这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计微专题概率与统计的创新问题课件,共45页。PPT课件主要包含了专题六概率与统计,ABC等内容,欢迎下载使用。
新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第2讲随机变量及其分布列课件: 这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题6概率与统计第2讲随机变量及其分布列课件,共60页。PPT课件主要包含了专题六概率与统计,分析考情·明方向,真题研究·悟高考,考点突破·提能力等内容,欢迎下载使用。












