2023年河北省邢台市中考二模数学试题

这是一份2023年河北省邢台市中考二模数学试题，共15页。试卷主要包含了 已知，，则下列说法正确的是．， 有甲、乙两个算式等内容，欢迎下载使用。

注意事项：
1.本试卷共8页，总分120分，考试时间120分钟。
2.答题前，考生务必将姓名、准考证号填写在答题卡的相应位置。.
3.所有答案均在答题卡，上作答，在本试卷或草稿纸上作答无效。答题前，请仔细阅读答题卡上的“注意事项”，按照“注意事项”的规定答题。
4.答选择题时，用2B铅笔将答题卡上对应题目的答案标号涂黑；答非选择题时，请在答题卡上对应题目的答题区域内答题。
5.考试结束时，请将本试卷和答题卡一并交回。
一、选择题（共16小题，1~10小题，每小题3分；11~16小题，每小题2分，共计42分.在每小题给出的四个选项中，只有一个选项是符合题目要求的）
1. 如图，以为端点，画一条射线，若射线与直线相交，则这条射线还可能经过的点是（ ）

A. 点B. 点C. 点D. 点
2. 墨迹覆盖了等式“”中的运算符号，则覆盖的是（ ）
A. ＋B. －C. －或×D. ＋或÷
3. 如图，矩形的顶点、在数轴上，且点表示的数为，点表示的数为4，则长为（ ）
A. 12B. 7C. 6D. 1
4. 某品牌手机上使用芯片的长用科学记数法表示为，则（ ）
A. 小于0B. 大于1
C. 在0与1之间，接近于1D. 在0与1之间，接近于0
5. 如图，将折叠，使边落在边上，展开后得到折痕，再将折叠，使边落在边上，展开后得到折痕，若与交点为，则点是（ ）

A. 外心B. 的内心
C. 的重心D. 的中心
6. 已知，，则下列说法正确的是（ ）．
A. B.
C. 、可能相等D. 、大小不能确定
7. 如图，四边形是由四边形平移得到的，若，，则的长可能是（ ）

A. 3B. 5C. 8D. 11
8. 有甲、乙两个算式：
甲：；乙：
说法正确的是（ ）
A. 甲对B. 乙对C. 甲、乙均对D. 甲、乙均不对
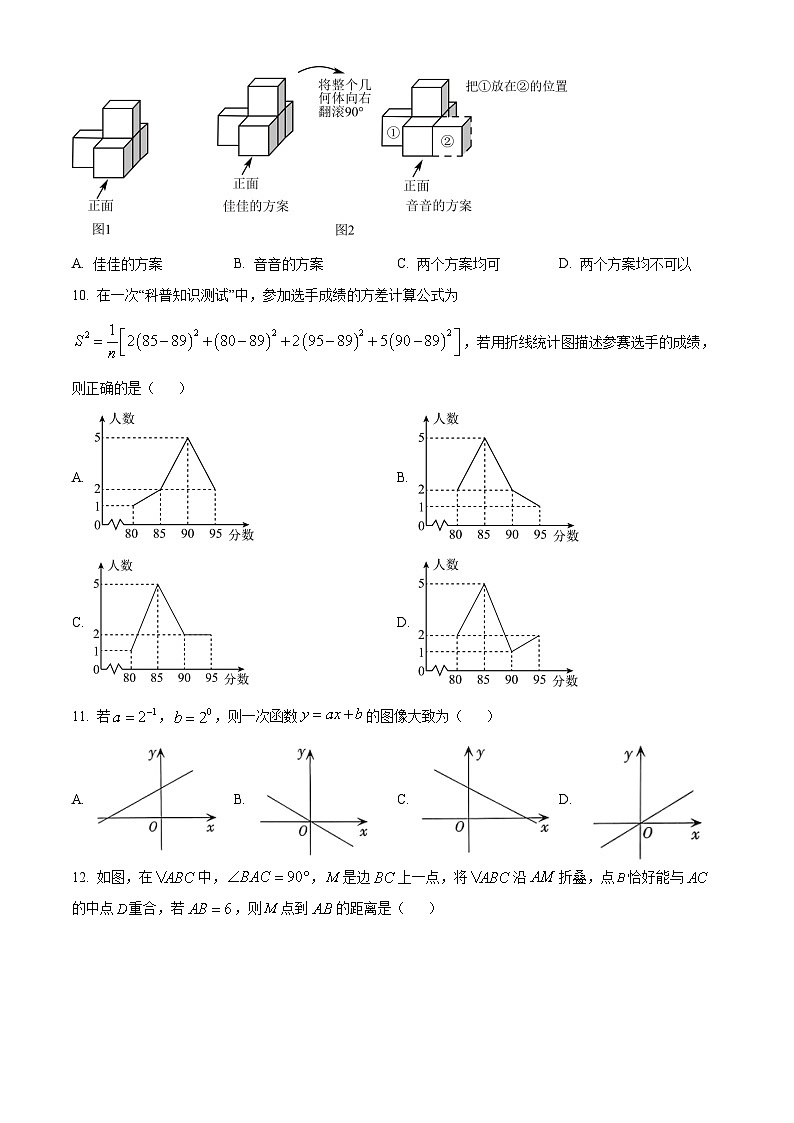
9. 如图1是有五个相同的小正方体粘在一起的几何体，图2是佳佳、音音对几何体分别设计了不同的操作方案，其中能使左视图保持不变的是（ ）

A. 佳佳的方案B. 音音的方案C. 两个方案均可D. 两个方案均不可以
10. 在一次“科普知识测试”中，参加选手成绩的方差计算公式为，若用折线统计图描述参赛选手的成绩，则正确的是（ ）
A. B.
C. D.
11. 若，，则一次函数的图像大致为（ ）
A. B. C. D.
12. 如图，在中，，是边上一点，将沿折叠，点恰好能与的中点重合，若，则点到的距离是（ ）

A. 3B. 4C. 5D. 6
13. 若不等式组的解集是，则不等式②可以是（ ）
A. B. C. D.
14. 下列四个菱形中分别标注了部分数据，根据所标数据，可以判断菱形是正方形的是（ ）
A. B.
C. D.
15. 已知 a比b大2，代数式当值为，则“”可以是（ ）
A. B. C. D.
16. 对于几何作图“过直线外一点作这条直线平行线”，给出以下两种方案：
方案Ⅰ：①在直线上取一点，作射线，以点为圆心，长为半径画弧，交线段的延长线于点；
②在直线上取一点（不与点重合），作射线，以点为圆心，长为半径画弧，交线段的延长线于点；
③作直线．所以直线就是所求作的直线．
方案Ⅱ：①在直线上取一点，以点为圆心，长为半径画半圆，交直线于，两点；
②连接，以为圆心，长为半径画弧，交半圆于点；
③作直线，所以直线就是所求作的直线．
对于以上两个方案，判断正确的是（ ）
A. 方案Ⅰ正确B. 方案Ⅱ正确
C. 方案Ⅰ、Ⅱ均正确D. 方案Ⅰ、Ⅱ均不正确
二、填空题（本大题共3个小题，每小题3分，共9分.其中18小题第一空2分，第二空1分，19小题每空1分）
17. 如图，在平面直角坐标系中，过点且平行轴的直线交双曲线于点，则________．
18. 已知二元一次方程组：
（1）请把方程②写成用的代数式表示________.
（2）这个方程组的解是_________.
19. 魏晋时期，伟大数学家刘徽利用如图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类证明了勾股定理．已知四边形、四边形、四边形均为正方形．

（1）若，，则_________，_________．
（2）连接交于点，则_________．
三、解答题（共7小题，满分69分，解答应写出文字说明、证明过程或演算步骤）
20. 某饮食集团4月份营业情况如下表所示，盈利记为正，亏损记为负（单位：万元）
（1）求出亏损的总天数；
（2）请通过计算，说明该饮食集团4月份是否盈利.
21. 发现三个连续的正整数，中间正整数的平方的3倍与2的和等于这三个正整数的平方和；
验证：请把表示成三个连续的正整数的平方和；
探究：设“发现”中的中间正整数为n，请论证“发现”中的结论正确．
22. 问题在甲、乙两个不透明盒子里分别装有完全相同的3个球和2个球，甲盒中3个球上分别标有数字1，1，2，乙盒中2个球上分别标有数字1，2；现从甲、乙两个盒子中分别摸出一个球，求恰好摸到两个球所标数字相同的概率.
（1）已知嘉淇的解法是错误的，他开始出现错误的步骤是_________.
（2）请用画树状图法给出正确的求解过程.
23. 如图，在和中，，，边交边于点，且．

（1）求证：；
（2）如图，当点恰好落在边上，若，求的长．
24. 某企业接到一批定单，在160天内（含160天）生产甲、乙两种型号家具共100套，经过测试与统计，得到如下数据：
受条件限制，两种型号的家具不能同时生产，已知该企业能如期完成生产任务，设生产甲型家具套，生产这100套家具的总利润为（万元）.
（1）求与之间的函数关系式；
（2）求为何值时，最大，最大值多少?
（3）由于客户需要，生产乙型家具需添加一道工序，此道工序平均每套家具所需费用为（万元），若随增大而减小，求的取值范围.
25. 已知，在平行四边形中，，，

（1）点在边上，连接．
①如图1，延长交的延长线于点，若，求的长；
②将绕点逆时针旋转120°得到，求的长的最小值；
（2）如图2，过点作于点，点在边上，且，点是射线上一点，以为圆心，为半径的圆与边只有一个交点时，求的取值范围．
26. 在平面直角坐标系中，抛物线（为常数，）与轴交于和两点，与轴交于点．
（1）请用含的代数式表示；
（2）当时，
①若抛物线的最小值为，求点的坐标；
②已知点在抛物线上，若，求的取值范围；
（3）作直线（是常数，且）交抛物线于、两点，若，直接写出的取值范围．
营业情况（单位：万元）
－9
－5
－2
2
8
10
天数
4
3
7
10
1
5
嘉淇用画树状图法进行求解，过程如下：
从甲盒摸球
从乙盒摸球
开始
①
②
结果
③
一共有四种等可能结果，其中恰好摸到两个球所标数字相同有两种等可能结果，因此P（恰好摸到两个球所标数字相同） ④
型号
制造每套家具平均用时（天）
每套家具的利润（万元）
甲
0.5
乙
0.8
2023年河北省邢台市初中毕业生升学文化课模拟考试（二）
（参考答案）
选择题、填空题答案速查
20.解：（1）亏损的总天数为.
答：亏损的总天数为14天.
（2）
.
答：该饮食集团4月份盈利13万元．
21.解：因为三个连续的正整数，中间正整数的平方的3倍与2的和等于这三个正整数的平方和，且把表示成三个连续的正整数的平方和
则三个连续的正整数的中间正整数为2，那么三个连续的正整数分别是1，2，3，
所以；
设“发现”中的中间正整数为n，
那么三个连续的正整数分别是，n，，
则，
即．
22.解：他开始出现错误的步骤是①，原因是他认为甲盒中有两个球，
（2）树状图如下图所示：
一共有六种等可能结果，其中恰好摸到两个球所标数字相同有三种等可能结果，因此（恰好摸到两个球所标数字相同）.
23.（1）证明：，
，即，
在和中，，
．
（2）解：，
，
，
是等边三角形，
，，
，
，
如图，过作于点，

，
，
，
，
，
，
．
24.解（1）.
（2）由题意得，，
解得，
，随增大而减小，
时，最大，最大值为（万元）.
（3），
随增大而减小，
，解得，，
.
25.解：（1）①∵四边形是平行四边形，
，
∴，而，
，
，
.
②将绕点逆时针旋转得到，
∴当最小时，最小；
当于点时，最小，
，，，
，，
的长的最小值．

（2）四边形是平行四边形，
，，
过点作于点，点在边上，且，
，
，
，
如图，当与相切于点时，与线段只有一个交点，

连接，
，
，
四边形为矩形，
，
当经过点时，连接，过作于点，

，，
，
，
，
，
，
当过点时，，

此时，点在点处，
，
的取值范围为或．
26.解：（1）抛物线与轴交于，
，
（2）①，
，
当时，有最小值，
，
解得，
抛物线的表达式为，
；
②设抛物线顶点为，所以，
抛物线与轴交于和两点，
令，
解得，
，
，
以直径作，当与抛物线有交点时，存在，
点在圆上或圆外，如图所示，

，
，
，
；
（3）根据题意画出图如图所示：

当时，，
当时，，
解得，
，
解得；
当时，，
当时，，
解得，
，
解得，
综上所述：或．
1
2
3
4
5
6
7
8
D
D
B
D
B
A
C
D
9
10
11
12
13
14
15
16
C
A
A
B
A
B
C
C
17. 18.（1） ;（2） 19.（1）7 12； ;（2）
从甲盒摸球
从乙盒摸球
结果