03空间向量与立体几何-湖南省2023-2024学年高二上学期期末数学专题练习（人教版）

这是一份03空间向量与立体几何-湖南省2023-2024学年高二上学期期末数学专题练习（人教版），共38页。试卷主要包含了单选题，多选题，填空题，解答题，证明题等内容，欢迎下载使用。
一、单选题
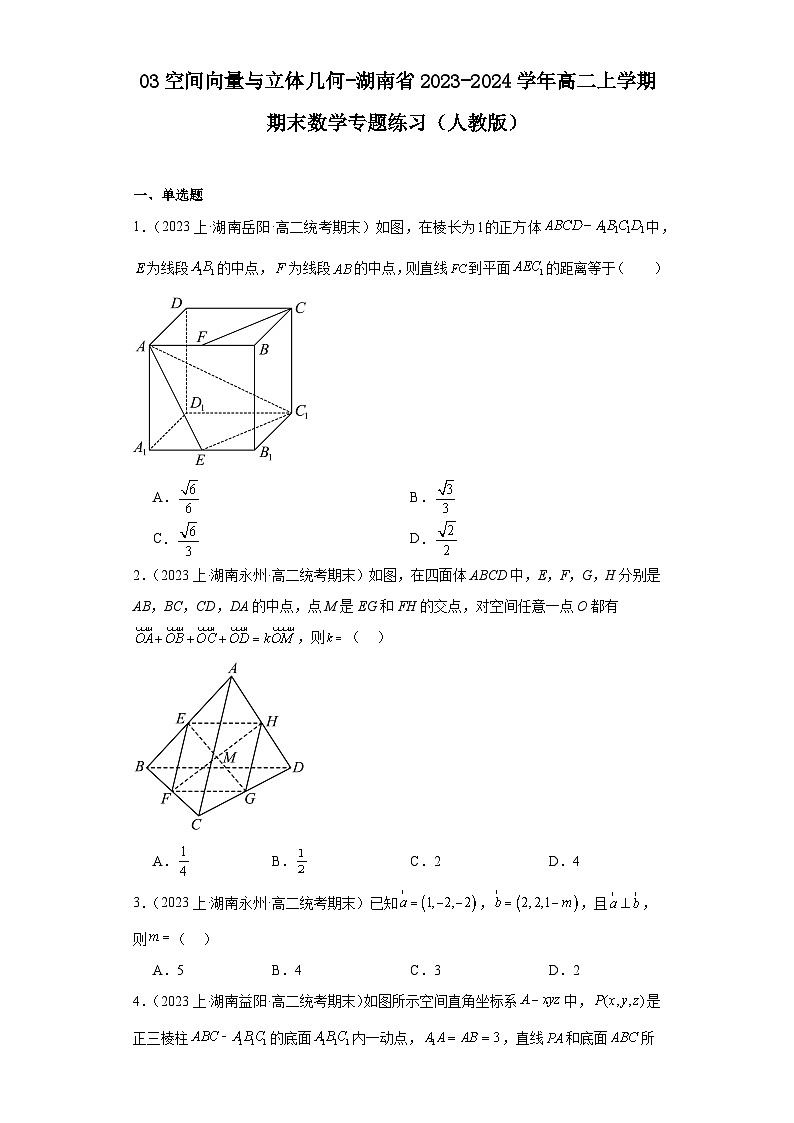
1．（2023上·湖南岳阳·高二统考期末）如图，在棱长为的正方体中，为线段的中点，为线段的中点，则直线到平面的距离等于（ ）
A．B．
C．D．
2．（2023上·湖南永州·高二统考期末）如图，在四面体ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点，点M是EG和FH的交点，对空间任意一点О都有，则（ ）
A．B．C．2D．4
3．（2023上·湖南永州·高二统考期末）已知，，且，则（ ）
A．5B．4C．3D．2
4．（2023上·湖南益阳·高二统考期末）如图所示空间直角坐标系中，是正三棱柱的底面内一动点，，直线和底面所成角为，则P点坐标满足（ ）
A．B．C．D．
5．（2023上·湖南益阳·高二统考期末）在四面体中，，M，N分别为的中点，则（ ）
A．B．
C．D．
6．（2023上·湖南益阳·高二统考期末）已知两个向量，若，则m的值为（ ）
A．B．C．2D．4
7．（2023上·湖南郴州·高二统考期末）已知四棱柱的底面是平行四边形，点E在线段上满足，，则（ ）
A．B．C．D．
二、多选题
8．（2023上·湖南衡阳·高二校考期末）如图，在棱长为2的正方体中，是线段的中点，点满足，，其中，则（ ）
A．存在，使得
B．当取最小值时，
C．当时，直线与平面所成角的正弦值为
D．当时，过三点的平面截正方体得到的截面多边形面积为
9．（2023上·湖南永州·高二统考期末）在长方体中，，E，F为的两个三等分点，点P是长方体表面上的动点，则（ ）
A．的最小值为B．的最大值为2
C．的最小值为30°D．的最大值为90°
10．（2023上·湖南益阳·高二统考期末）已知正方体的边长为1，E是棱的中点，则（ ）
A．B．C．D．
11．（2023上·湖南株洲·高二校考期末）已知圆柱底面半径，高，下底面圆心为O，上底面圆心为，A是下底面圆上任意一点，B是上底面圆上任意一点，则下列命题中正确的是（ ）
A．向量与的夹角为定值B．的最大值为
C．与夹角的最大值为D．
三、填空题
12．（2023上·湖南永州·高二统考期末）在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体，该几何体的上下底面平行，且均为扇环形（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，，，，均与曲池的底面垂直，且，每个底面扇环对应的两个圆的半径分别为1和2，对应的圆心角为90°，则直线与所成角的余弦值为 ．
13．（2023上·湖南衡阳·高二校考期末）如图，在直三棱柱中，，、分别为棱、的中点，则 .
14．（2023上·湖南益阳·高二统考期末）在长方体中，，点E为棱上靠近点C的三等分点，点F是长方形内一动点（含边界），且直线与平面所成角的大小相等，则线段长度的取值范围为 ．
15．（2023上·湖南益阳·高二统考期末）已知两个向量，则 ．
16．（2023上·湖南长沙·高二统考期末）已知空间向量，若，则 ．
17．（2023上·湖南怀化·高二统考期末）如图，已知正方体中，分别为中点，，则到平面的距离是 ．
18．（2023上·湖南娄底·高二校联考期末）如图，在空间四边形中，若，，，则 .
四、解答题
19．（2023上·湖南衡阳·高二校考期末）如图，直四棱柱的底面是菱形，，，，分别是的中点.
(1)证明：平面.
(2)求平面与平面所成角的余弦值.
20．（2023上·湖南永州·高二统考期末）如图，在三棱锥中，，平面平面，，，．
(1)证明：平面；
(2)若点D在线段AC上，直线PD与直线BC所成的角为，求平面DBP与平面CBP夹角的余弦值．
21．（2023上·湖南永州·高二统考期末）如图，在正方体中，为的中点．
(1)证明：直线平面；
(2)求直线与平面所成角的正弦值．
22．（2023上·湖南长沙·高二雅礼中学统考期末）如图所示，在直三棱柱中，，为的中点.
(1)直线与平面的交点记为，直线与平面的交点记为.证明：直线平面.
(2)求二面角的大小；
23．（2023上·湖南郴州·高二统考期末）已知空间向量，，，，．
(1)求x，y，z；
(2)求与所成角的余弦值．
五、证明题
24．（2023上·湖南邵阳·高二统考期末）如图，四棱锥的底面是边长为2的正方形，平面平面，是斜边的长为的等腰直角三角形，E，F分别是棱，的中点，M是棱上一点，
(1)求证：平面平面；
(2)若直线与平面所成角的正切值为，求平面与平面夹角的余弦值．
25．（2023上·湖南岳阳·高二统考期末）如图，在三棱锥中，底面，，点，，分别为棱，，的中点，是线段的中点，，.
(1)求证：平面.
(2)已知点在棱上，且直线与直线所成角的余弦值为，求线段的长.
26．（2023下·湖南湘潭·高二统考期末）如图，在四棱锥中，底面，底面是正方形，与相交于点E，点F在线段上，且.
(1)求证：平面；
(2)求平面与平面夹角的正弦值.
27．（2023上·湖南益阳·高二统考期末）如图甲，在矩形中，，E为线段的中点，将沿直线折起，使得平面平面，如图乙．
(1)求证：平面；
(2)线段上是否存在一点H，使得二面角的余弦值为？若存在，请确定H点的位置；若不存在，说明理由．
28．（2023上·湖南张家界·高二统考期末）如图，在五面体中，平面，为直角梯形，，，．
(1)若为的中点，求证：平面；
(2)求平面与平面夹角的余弦值．
29．（2023上·湖南郴州·高二统考期末）如图2，在中，，，．将沿翻折，使点D到达点P位置（如图3），且平面平面．
(1)求证：平面平面；
(2)设Q是线段上一点，满足，试问：是否存在一个实数，使得平面与平面的夹角的余弦值为，若存在，求出的值；若不存在，请说明理由．
30．（2023上·湖南株洲·高二校考期末）如图，正方体的棱长为2，E、F分别为和的中点，P为棱上的动点.
(1)若点P与重合，求证：平面；
(2)当平面与平面所成锐二面角的正弦值最小时，求的值.
参考答案：
1．A
【分析】以点为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，利用空间向量法可求得直线到平面的距离.
【详解】以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，
则点、、、、，
，，则，所以，，
因为平面，平面，平面，
设平面的法向量为，，，
则，取，可得，
，所以，直线到平面的距离为.
故选：A.
2．D
【分析】证明出四边形为平行四边形，为中点，利用空间向量基本定理求解即可.
【详解】E，F，G，H分别是AB，BC，CD，DA的中点，
故，，
所以四点共面，且四边形为平行四边形，
故为中点，
因为，，
所以，
故.
故选：D
3．D
【分析】利用向量垂直充要条件列出关于的方程，解之即可求得的值.
【详解】，，且，
则，则，解之得
故选：D
4．A
【分析】根据空间直角坐标系求得，以及平面的一个法向量，根据线面夹角的坐标运算即可得P点坐标满足的等式关系.
【详解】解：由正三棱柱，且，根据坐标系可得：
，又是正三棱柱的底面内一动点，则，所以，
又平面，所以是平面的一个法向量，
因为直线和底面所成角为，
所以，
整理得，又，所以.
故选：A.
5．D
【分析】根据空间向量的线性运算，即可得出答案.
【详解】由题意得：.
故选：D.
6．D
【分析】根据空间向量平行得到方程组，求出m的值.
【详解】由题意得，即，
解得：，故m的值为4.
故选：D
7．A
【分析】用空间基底向量表示向量结合空间向量线性运算求解.
【详解】∵，则，
∴.
故选：A.
8．BCD
【分析】建立空间直角坐标系，利用向量空间中的垂直，距离，夹角等问题.
【详解】以D为坐标原点， 的方向分别为轴的正方向，建立如图所示空间直角坐标系，
则，，，，，，
， 。
，
，
若，则 即,
因为，显然，所以不成立，A错误；
最小时，是的公垂线段，，，
，
，解得，B正确．
当 ， ， ， ，
设平面的法向量为，
则 取，则，
.故直线与平面所成角的正弦值为 ，C正确
当 时，在取靠近点的三等分点，连接并延长交于点，易得点是靠近点的三等分点，取靠近点的三等分点，如图所示，
过三点的平面截正方体得到的截面多边形为四边形，
则，且，又因为平面，所以，即，
则四边形为矩形，又，，求得面积为 ， D正确.
故选：BCD
【点睛】方法点睛：空间中的动点问题是指在一定的约束条件下，点的位置发生变化，在变化过程中找出规律，将动点问题转化为“定点”问题、将空间问题转化为平面问题、将立体几何的问题转化为解析几何的问题等，目的是把问题回归到最本质的定义，定理或现有的结论中去，也可以通过建系用坐标法构建函数，或者借助空间向量求得结果.
9．BD
【分析】建立空间直角坐标系，得到点的坐标，分析出P位于长方体的四个侧面时情况相同，P位于长方体的上下两个平面时情况相同，分两种情况进行求解出，得到最值，并分析出的最大值，举出反例得到C错误.
【详解】以A为坐标原点，分别以为轴，建立空间直角坐标系，
因为，所以，
不妨设，故，，
由对称性可知：P位于长方体的四个侧面时，所处情况相同，
不妨设，
则
，
故当时，的最小值为，此时
当或2，或1时，的最大值为2，
由对称性可知：P位于长方体的上下两个平面时，所处情况相同，
不妨设，
则
，
故当时，的最小值为0，
当或2，时，的最大值为2，
综上：的最小值为0，的最大值为2，A错误，B正确；
因为的最小值为0，故的最小值为0，
因为，所以的最大值为90°，D正确；
当点与点重合时，此时，C错误.
故选：BD
10．BC
【分析】建立空间直角坐标系,用空间向量计算验证各选项.
【详解】
以为原点,为轴的正方向建系如图:
,

对A:因为,所以不成立;
对B:,故,故B正确;
对C:,故C正确;
对D:, ,而,故D错误,
故选:BC
11．ACD
【分析】建立合理的空间直角坐标系，设，，利用向量夹角公式即可判断A,C，利用向量坐标化的数量积计算即可判断B，利用向量模长的相关计算方法即可判断D.
【详解】以下底面互相垂直的两条直径和上下底面圆心连线为坐标轴建立空间直角坐标系；
对A，由圆柱底面半径，高，
则可设，，其中
，则，
因为，所以，故A正确；
对B，，
，则，则，则，
所以的最大值为1，故B错误；
对C，
，
因为，所以，
所以与夹角的最大值为，故C正确；
对D，，
，
，故，故D正确.
故选：ACD.
12．/
【分析】建立空间直角坐标系，利用空间向量即可求得直线与所成角的余弦值.
【详解】延长AB交CD于O，过点O作平面，
以O为原点，分别以OD，OA，OT所在直线为x，y，z轴建立空间直角坐标系.
则，，，，
则，，
则，
则直线与所成角的余弦值.
故答案为：
13．
【分析】分析可知，，利用空间向量数量积的运算性质可求得的值.
【详解】因为平面，平面，则，同理可知，
所以，
.
故答案为：.
14．
【分析】根据已知建立以点为原点，向量方向分别为轴正方向的空间直角坐标，得出，，，根据点F是长方形内一动点（含边界），设，其中，，得出平面的一个法向量可以为，根据直线与平面所成角的大小相等，得出，化简得出，结合，，得出，即可根据两点间距离的坐标公式得出，即可根据二次函数值域与根式不等式得出答案.
【详解】为长方体，
两两垂直，
以点为原点，向量方向分别为轴正方向如图建立空间直角坐标系，
则，，
点F是长方形内一动点（含边界），
设，其中，，
则，，
平面的一个法向量可以为，
直线与平面所成角的大小相等，
设直线与平面所成角的大小，
则直线与平面所成角的大小，
，
，即，
整理得：，即，
，，
，解得，
，
，
，
，
，
，
，
则，
故答案为：.
15．
【分析】根据空间向量坐标的线性运算直接求解即可.
【详解】解：已知两个向量，
则.
故答案为：.
16．
【分析】由空间向量的坐标运算求解即可.
【详解】因为，所以存在实数k，使得，即，
所以解得，，，.
故答案为：
17．/
【分析】利用坐标法，根据点到平面的距离向量求法即得.
【详解】如图建立空间直角坐标系，则，
所以，
设平面的法向量为，
则，令，则，
所以到平面的距离是.
故答案为：.
18．
【分析】由向量的运算法则即得
【详解】因为，，，
所以，
故答案为：
19．(1)证明过程见详解
(2)
【分析】（1）取的中点，连接，根据中点得到平行关系，利用线面平行和面面平行的判定得面面平行，进而得证；
（2）建立空间直角坐标系，求出相应点的坐标，分别求出平面与平面的法向量，然后利用向量的夹角公式即可求解.
【详解】（1）取的中点，连接，
因为且，所以四边形为平行四边形，则，
又分别为的中点，所以，所以，
又平面，平面，所以平面，
因为分别为的中点，所以且，
又因为且，所以且，
所以四边形为平行四边形，则，
又平面，平面，所以平面，
因为，平面，
所以平面平面，
因为平面，所以平面.
.
（2）取的中点，连接，
因为且为菱形，所以，则，
又因为四棱柱为直棱柱，所以平面，
又因为平面，所以，
则两两互相垂直，所以建立如图所示空间直角坐标系，
因为，所以，，，，，
则，，
设平面的法向量，则，即，
令，则，所以，
易知平面的一个法向量为，
设平面与平面所成角为，则，
所以平面与平面所成角的余弦值为.
20．(1)证明见解析
(2)
【分析】（1）由勾股定理证明，由已知面面垂直证明线面垂直，再到线面垂直，从而证得结果；
（2）建立空间直角坐标系, 由直线PD与直线BC所成的角，求得点坐标，再求平面DBP与平面CBP的法向量，得出两平面夹角的余弦值．
【详解】（1）证明：在中，因为，，，
所以，所以，
因为，平面平面，平面平面，平面，
所以平面，
因为平面，所以，
又，，平面，
所以平面．
（2）以B为坐标原点，BA为x轴正方向，BC为y轴正方向，过B垂直于平面ABC的直线为z轴，建立如图所示的空间直角坐标系，
由题意得，， ，平面平面，平面平面，过点作于点，则平面ABC，，，则，
所以，，，，
设点，，
则，
所以，，，
所以点坐标为，
所以
因为直线与直线所成的角为，
，解得
所以点坐标为，则．
设平面的法向量为
则，取，可得．
因为平面，
所以平面的一个法向量为，所以
所以平面与平面夹角的余弦值．
21．(1)证明见解析
(2)
【分析】（1）先利用中位线定理证得，再利用线面平行的判定定理即可得证；
（2）建立空间直角坐标系，分别求出与平面的法向量，从而利用空间向量夹角余弦的坐标表示即可得解.
【详解】（1）连接直线BD，设直线BD交直线AC于点O，连接EO，如图，
因为在正方体中，底面是正方形，所以O为BD中点，
又因为E为的中点，所以，
又因为平面，平面，
所以直线平面．
（2）根据题意，以DA为x轴，DC为y轴，为z轴建立如图所示的空间直角坐标系，如图，
不妨设正方体的棱长为2，则，，，，
故，，，
设平面的法向量，则，即，
令，则，，故，
设直线与平面所成角为，则，
所以直线与平面所成角的正弦值为．
22．(1)证明见解析
(2)
【分析】（1）由题意可知，两两垂直，分别以为x轴，y轴，z轴建立如图所示的空间直角坐标系，可得，进而得到，从而得证；
（2）求得平面平面和平面的法向量，进而求解.
【详解】（1）根据题意知，两两垂直，
分别以为x轴，y轴，z轴建立如图所示的空间直角坐标系.
因为，E为的中点.
所以，
所以.
直线与的交点即为直线与平面的交点M，
直线与的交点即为直线与平面的交点N，
所以.
所以，
所以，又平面平面，
所以直线平面.
（2）设G为的中点，则，，
因为平面平面，平面平面，且平面，
所以平面，
所以平面的一个法向量.
由，
设是平面的法向量，
则，，
令，得，即，
所以二面角的大小是.
23．(1)，，
(2)
【分析】（1）根据空间向量平行及垂直的坐标关系可得x，y，z的值；
（2）利用空间向量坐标运算求得，，即可得，，再根据夹角余弦公式求得与所成角的余弦值即可．
【详解】（1）解：由得，解得，，经检验符合；
由得，解得
，，．
（2）解：由（1）可得，，
，，
．
24．(1)证明见解析
(2)
【分析】（1）根据面面垂直的性质定理可得平面，从而，又，由线面垂直的判定定理得平面，则，又，得平面，根据面面垂直的判定定理即可证得结论；
（2）取的中点，则，，结合（1）得平面，结合线面角的定义得是直线与平面所成角，求得，，建立空间直角坐标系，分别求出平面、的法向量，利用空间向量夹角公式进行求解即可.
【详解】（1）因为是斜边PA的长为的等腰直角三角形，所以，，
又平面平面，平面平面，平面，
∴平面，又平面，∴，
又，，平面，∴平面，
因为平面，∴，
∵，F是棱PC的中点，∴，
又，平面，∴平面．
又平面，∴平面平面．
（2）如图，取的中点，连接，，
则，，
由（1）知平面，∴平面，
∴是直线与平面所成角，
∴，
∴，∴，
以为坐标原点，，，分别为轴，轴，轴建立空间直角坐标系，
则有：，，，，
∴，，，
设平面的法向量为，平面的法向量为
则，令，则，
有，令，则，
∴，
∴平面与平面夹角的余弦值为．
25．(1)证明见解析
(2)或2
【分析】（1）以为原点，为轴，为轴，为轴，建立空间直角坐标系，利用向量法能证明平面；
（2）设，且，则,0,，由直线与直线所成角的余弦值，利用向量法能求出线段的长．
【详解】（1）如图，以为原点，为轴，为轴，为轴，建立空间直角坐标系，
则,0,，,0,，,4,，,2,，,0,，,2,，
,2,，,0,，,2,，
设平面的法向量,,，
则，取，得,0,，
，平面，平面．
（2）设，且，则,0,，,,，,2,，
则，整理得
解得或，所以线段AH的长为或2．
26．(1)见解析
(2)
【分析】（1）建立空间直角坐标系，利用向量的垂直关系证明线线垂直，即可由线面垂直的判断求证，
（2）建立空间直角坐标系，利用平面法向量的夹角即可求解.
【详解】（1）以为原点，为轴，为轴，为轴，建立空间直角坐标系，
设，则
故,由得,所以,
， ，
由于因此，
进而,又平面,
故平面；
（2），
设平面的法向量，，，
则，取，得，
平面的法向量，
则，取，得，
设平面与平面的夹角，
则．
．
27．(1)证明见解析
(2)存在，点H是线段的靠近B点的三等分点
【分析】(1) 取线段的中点O，连接，得到，根据面面垂直得到线面垂直，进而得到，然后利用勾股定理和线面垂直的判定即可求解；
(2)建立空间直角坐标系，求出对应点的坐标，设，分别求出平面和平面的法向量，利用向量的夹角公式和二面角的余弦值即可求解.
【详解】（1）取线段的中点O，连接，
在中，，
∴，又平面平面，
平面平面，平面
∴平面，又平面，∴．
又，则，∴，
又，平面ADE，∴平面．
（2）过E作的平行线l，以E为原点，分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系，则，平面的法向量，
设，则，
设平面的法向量为，
则,即，
令，则，∴
由题意可知二面角为锐二面角，
所以，，解之得：，或（舍），
所以，点H是线段的靠近B点的三等分点．
28．(1)证明见解析
(2)
【分析】(1)利用线线平行证明线面平行；
(2)利用空间向量的坐标运算求面面夹角的余弦值.
【详解】（1）取的中点，连接，，
因为，分别是，的中点，
所以且，
因为，，
所以且，所以四边形为
所以
又平面，平面，所以平面；
（2）以为原点，，所在直线分别为轴和轴，
建立如图所示的空间直角坐标系，不妨设，
则，，，，，
，，，
设平面的法向量为，
则，，
令，得，
设平面的法向量为，
则，，
令，得，
故，
所以平面与平面夹角的余弦值为．
29．(1)证明见解析
(2)存在，
【分析】（1）利用余弦定理求出的长，由勾股定理得，过点作，然后利用面面垂直的性质定理及判定定理证明即可，
（2）建立空间直角坐标系，利用法向量建立关系式分析即可.
【详解】（1）在中，由余弦定理得，
，
，
过点作交于点，如图所示，
又平面平面，且平面平面
由平面，
所以平面，又平面，
所以，又，
所以平面，又平面，
所以平面平面．
（2）由题知，即，
由（1）知，且
平面，所以以A为原点，建立如图所示的空间直角坐标系，
则，，
设为平面的法向量，
由，
令得，
且，
又易得平面的法向量为，
由，
故存在实数使得平面与平面的夹角的余弦值为．
30．(1)证明见解析
(2)
【分析】(1)建立空间直角坐标系，利用向量方法证明，，结合线面垂直判定定理证明结论；
(2)利用向量方法求平面与平面所成锐二面角的余弦值，根据同角关系求其正弦，再求其最小值确定的值.
【详解】（1）在正方体中，建立如图所示的空间直角坐标系，
因为、分别为和的中点，与重合，
则，，，，，
，，，
由，即，
由，即，
而，且，平面，
因此，平面，
（2）在（1）的空间直角坐标系中，设，，，，
令平面的法向量为，
则令，得，
所以为平面的一个法向量，
又为平面的一个法向量，
设平面与平面所成的锐二面角为，
则，
当且仅当时取等号，
因此，当，即时，取最大值，
所以，当且仅当时取等号，
所以当时，平面与平面所成锐二面角的正弦值最小时，
此时.